长期护理保险定价模型分析※

李玉水 叶小丹

（福建江夏学院，福建 福州 350108）

随着我国人口老龄化加深，其老年人口的数量也逐渐增多，老龄化呈现出不断增长趋势，失能、贫困等因此成为了社会突出问题。一是老年人口数量呈爆发式增长。截至2015年，60岁以上的老年人口已经达到了2.2亿，占全国总人口的16.1%，估计到2025年将会冲破3亿。二是空巢以及高龄老年人口的增多。空巢的老年人口已经超过了1亿人，80岁以上老人达到了2400万。三是老年人的身体状况让人担忧。半数以上的高龄老人患有慢性病，失能半失能老年人约4000万。在中国，人口老龄化形势日渐严峻，但是民营的养老机构身为养老服务主力军却面临着护工短缺，不仅专业护工短缺，而且对于日常照料都人手不足。因此，如何更好的“养”老人也成为了许多国民所担心的问题，这使得长期护理保险存在大量潜在需求。

我国老龄失能人口数一直是随着人口数增加而呈现上升趋势，据2010年第六次人口普查所得出60～64 岁、65～69岁、70～74 岁、75～79 岁、80～84岁、85～89岁、90～94岁、90岁及以上年龄段需要生活护理的比例分别为0.88% 、1.51% 、2.67%、4.33%、7.97%、 12.68% 、20.96% 、26.37% ，数据表明，失能人口随着年龄增加而增加。根据2006年至2014年1‰人口变动调查抽样数据进行预测得出2015年至2025年的抽样人口数。据此使用MATLAB预测得出2015年至2025年分年龄段失能人数，如图1所示。随着年数的增加，各年龄段的失能人口不断增加，失能率也逐渐增加，当处于相同年数时，由于人的生命周期性，失能人数随着存活时间先呈现递增后递减的趋势，但总体来说，失能人数是呈递增趋势。

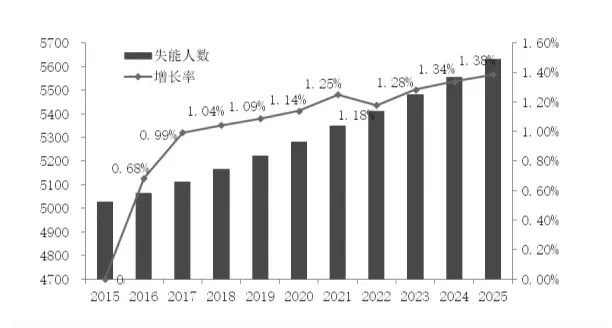
图1 2015年至2025年失能人口预测趋势图

由上图可知，我国失能人口数呈现增长模式，每年同比增长率也呈上升趋势，且每年都有失能人口的增加，这势必会影响长期护理保险的需求量，使得其在一定程度上能够获得群众认可，人们因此也更愿意通过购买长期护理保险来减轻由于护理费用所造成的负担。

我国护理产业严重落后，已与老龄化趋势形成强烈反差，应当引起高度重视，解决之道就在于建立社会的长期护理保险制度。长期护理保险作为“第六大保险”是对原有的社会保障体系的重要添补。建立长期护理保险制度对失能人员基本生活权利、利益的保障，促进养老业的发展和拓展护理人员的就业途径具有很大的作用，也是应对人口老龄化的主要举措。尽管医疗保险在一定范围内解决了失能、半失能人员的经济问题，但后期的护理却不理想。而长期护理保险不但保障了失能人员在医疗护理方面的需求，而且还造就了新式的医养结合模式，在某些方面上弥补了养老保险以及医疗保险的不足。

一、影响长期护理保险定价的因素及理论基础

(一)影响长期护理保险定价的因素

1.利率。保险的定价离不开对价值的计算，而随着时间的增加，其价值也因利率的变化而变化，或增加或减少。利率作为金融市场的要素之一，而保险作为金融业的主要企业，受到利率的影响是不可避免的，而且这种影响会随着保险行业扩大而加剧其影响。由于货币的时间价值，且长期护理保险又是属于长期性的人身保险，利率的大小在一定程度上随着时间长短影响着长期护理保险的定价，因此，利率是影响长护险产品定价的一个重要指标，在进行精算模型的构建时要充分考虑到利率对其影响。

2.通货膨胀。和利率一样，在存在通货膨胀的情况下，社会经济生活必将因此产生影响，使得人们所持有现金量将缩减，购买力下降。对于身体出现健康问题的人群来说，由于通货膨胀，其所领取到的保险给付金将无法达到其预期，甚至对于其治理疾病来说是杯水车薪、无济于事的。因此，在建立保险精算模型时，应慎重的考虑到通货膨胀对产品定价的所带来的影响。

3.护理率。指被保险人因为疾病或者是意外事故导致的生活不能自理的概率。可通过不能自理概率来进行产品定价。

4.失能率。即不能自理人数与总人数的比值，长期护理保险的赔付条件就是被保险人是否失能，因此，失能率是长期护理保险定价模型的重要条件之一，在建立模型时候应考虑不同性别、不同年龄人口的失能率，以此提高定价模型的精确度，使得所建立模型更适合当前需长期护理的人员。

5.死亡率。死亡率在一定程度上决定了保险赔付是否实现，而长期护理保险是以被保险人年老、疾病或伤残为给付前提条件，身为保险公司（保险人），其需要防备是被保险人“过早生患病需护理”和“失能造成的护理时间过长”的风险，而这两者都会造成人们平均寿命的下降，因此，对于长期护理保险来说，选择合适的死亡率是至关重要的。

(二)理论基础

1.利息力累计函数。

一般假设利息力累计函数为一个Orentein-Uhlenbeck过程或者是wiener过程，本文将采用标准wiener过程进行利息力累计函数的建立，从而建立随机利率下的精算模型。常见的设利息力累计函数为：

δ（t）=δt+βU(t)(0≤t≤∞)

其中，δ，β均为常数且大于或等于零，δt为确定的部分，表示t时刻所获得的瞬间收益率为δ，而βU(t)为不确定部分，因此选用标准wiener过程进行刻画。

wiener过程是最普遍、典型的随机过程，其表示在给定二阶矩过程{U(t),t≥0}的条件下，其满足如下条件：

（1）{U(t),t≥0}具有平稳独立增量。

（2）对于∨t,s,其中 t＞s≥0，则有 U(t)-U(s)服从正态分布；若t≥0，则U(t)服从正态分布。

（3）若 t=0，则 U(0)=0。

当σ=1时，此wiener过程为一个标准wiener过程，其有限维分布服从正态分布，且其期望为E[U(t)]=0，方差为Var[U(t)]=σ2t=t。则贴现函数为 V(t)=e-δ(t)=e-δt-βU(t)，因此

2.曼联模型

曼联模型是JamesD.C.于1930年提出的，针对长期护理保险精算模型定价的一种方法。其基本的假设是：若(x)在x+t岁时因为发生失能，以后的护理周数只与x+t岁时的失能状况有关，而与x+t岁之前的状况都无关，即与在x岁时的状况无关，其与Markov的无后效性存在一定的相似性。该模型是通过护理率来计算保险费用，且其为了考虑利用到生存率、死亡率以及利率因子，因此护理率为每年计算。

对于曼联模型相关精算符号的解释如下：

lx：期初的生存人数，表示能生存到x岁的人的期望人数。

Lx：年龄[x,x+1]在岁之间的平均生存人数。

v：折现因子，v=(1+i)-1（其中为利率因子）。

假设保险金的给付是服从均匀分布，即被保险人在x：x+t期间发生失能状况，即进入不能自理状态需要护理费用的赔付，均匀分布假设均认为其是在x+t 2时刻发生失能状况。若t=1，则x：x+1岁之间的所有赔偿给付折现到x岁时的现值为v1/21/2PxSx（其中1/2Px=lx+1/2lx），若赔付发生在x+t-1：x+t期间内，则其现值为vt-1/2t-1/2PxSx+t-1。

设其趸缴纯保费为AS(x)，则

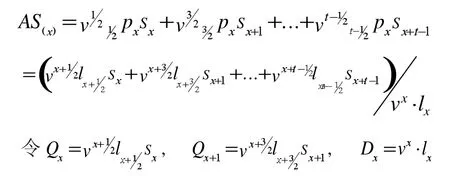
若存在n年保险期限，m年的保险金给付期限，不存在免责期，则

二、长期护理保险的精算模型

(一)精算假设

1.当被保险人年满60周岁及以上才能获得由于购买长期护理保险所带来保险金赔偿给付。投保人为40至80周岁之间的健康男女。

2.无附加保费，即不考虑退保率、费用率等附加费用，以方便模型的测算。

3.被保险人的健康状况只与其性别以及年龄相关，而与其何时参加保险并无关系，且本文假设新投保的人群其健康状态与之前相同年龄并已参加保险人群的健康状态相同。

4.假设长期护理保险的保险金给付分为两个方面，一是长期护理保险金给付，被保险人在其六十周岁之后逝世且在其逝世前取得了长期护理，即其进入失能状态。二是死亡保险金给付（包含因疾病或意外身故死亡），被保险人在六十周岁之后逝世而且逝世前并未接受长期护理，即默认为其未处于失能状态或未进入。

(二)模型设计

根据本文所提及的曼联模型来进行模型设计，假设年龄为的投保人购得年保险期限、给付年、无等待期的保险，若其接受了护理，则其给付护理保险金额为，若未接受护理则其死亡年末给付为，为年赔付额。据此分别建立固定利率水平和随机利率水平下长期护理保险的趸缴纯保费和期缴纯保费。

1.固定利率水平下长期护理保险精算模型

此时，趸缴纯保费为:

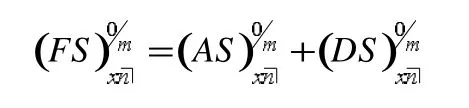
进一步，若限期h年所缴的均衡纯保费为hPx，

其中有关符号含义如下：

nqx：表示年龄为岁的人在未来n年内死亡的概率。

npx=1-nqx：表示年龄为x岁的人活过n年的概率。

n/qx：表示年龄为x岁的人在[x+n,x+n+1]死亡的概率。

nrx：表示x岁的人在n年内失能的概率。

nrx=1-nrx：表示x岁的人在n年内未失能的概率。

Sx：平均护理周数（护理率），如上文所介绍，Sx=，若引入失能总人数（即需长期护理的总人数），则年龄为x岁的失能的人的护理周数× x岁的人的失能率。

v：折现因子，v+(1+i)-1（其中为利率因子）。

f：通货膨胀率。

三、结论与展望

针对日益加剧的人口老龄化现状，继美国之后，欧洲各国以及日本都相继推出符合其国情的长期护理保险，而中国属于人口大国，其人口老龄化程度与其他发达国家相比就更加突出，问题也逐渐增加，随着人口老龄化加剧，失能老人数量也呈上升趋势，尽管医疗水平也在逐渐提升，但失能老人的增加速度却更加快，使得老人需要护理的成本也在逐渐增加，因此更需要长期护理保险的出现以及完善。

人保、太平以及国泰等寿险公司都向大众销售过长期护理保险，但是其几乎针对的是老年人群，无法保障中年或是中老年人群因疾病或意外伤害带来的费用损失，其保障范围是相对较低的。其次，保险公司销售的长期护理保险主要是面向中高收入人群的，其费用自然较高。2016年我国在多个地区进行长期护理保险的试点，而不是将长期护理作为社会保险方式面向广大群众。这在一定程度上说明了现行的长期护理保险还存在不足，其所保障范围还应完善，保险费用也应根据民众的生活条件进行制定，更应该让人们意识到长期护理保险的重要性。