基于PSO-GRA耦合决策的 排水沟系统多目标规划模型

帅雨婷，张展羽，冯宝平，吴蕴玉，郑成鑫

(1.河海大学水利水电学院，南京 210098；2.河海大学南方地区高效灌排与农业水土环境教育部重点实验室，南京 210098； 3.河海大学农业工程学院，南京 210098)

0 引 言

排水沟系统规划是农田水利规划的核心环节之一，对保障农田水分状况平衡、节省工程资金、增加粮食产量、减少污染物排放等具有重要意义。智能算法与多目标决策已广泛应用于农田水利工程规划研究。殷国玺等[1]针对南方丘陵地区构建控制排水多目标模型，并基于粒子群算法进行多目标优化。A Singh等[2]运用非线性规划模型优化印度哈里亚灌溉地区土地与水资源配置以获得最大净年收益。M Xi等[3]运用量子态粒子群算法(QPSO)校准根区水质模型(RZWQM2)参数，准确预测环境条件对水流、污染物水平的影响。K Yin等[4]运用改进的灰色关联分析处理多属性组决策问题并确定备选方案优先级。近年来，学者们针对排水沟塘湿地系统对稻田降雨径流中氮磷等污染物的削减效应及规律也开展了大量研究[5-7]。BM Phillips等[8]于加州中部海岸水域构建沟渠及组件模型探索了完整植被沟对农田排水径流中农药的削减。Verhoeven等[9,10]阐明了形式多样的湿地生态系统从流动水中有效去除营养物质的作用机理，通过沟渠-湿地-池塘系统(DWPS)处理河沟污水发现硝化和反硝化是与脱氮有关的最重要的过程。茆智等[11-14]运用灌区稻作区田间、草沟、塘堰湿地和骨干沟系统净化农田排水中的氮磷效果显著，且受沟塘空间分布、几何特征、水力联系、沟渠植物搭配方式、水力停留时间(HRT)等影响。

传统排水沟系统规划借助智能算法将问题转化为求费用目标极小或收益目标极大的单目标高阶隐函数问题，本质上限制了其蓄水滞涝效能，且忽视了其作为污染物输移主要廊道的附属生态效应，使得农田可持续利用受到制约，必须权衡多方效应将单一设计目标向多重目标转变。然而，将现有研究中论证的排水沟系统水质净化效应及影响因素的优化方向，量化应用于排水沟系统规划中的研究比较少，且权衡多目标间矛盾性进行优化决策的理论方法需要进一步探索。故本文在排水沟系统工程费用与产量效应基础上，综合考虑生态去污效应，构建排水沟系统多目标规划模型，运用粒子群算法耦合基于目标达成度的灰色关联投影法科学决策多目标规划方案，并以上海松江区高标准农田稻作区开展模型应用研究，探索适应现代可持续发展的排水沟系统优化规划新方法。

1 排水沟系统多目标规划模型构建

排水沟系统一般由干、支、斗、农4级固定沟道及蓄水承泄区等组成(见图1)。农田中由降雨产生的多余地面水和地下水通过农沟汇集，然后依次经斗、支、干沟排泄到承泄区。各级沟道相互垂直布置，长度根据当地机耕要求或区域规划决定，且下一级沟道长度决定上一级沟道的间距。不同的沟道间距、断面几何特征与排水历时组合直接影响排水沟系统的减污效果，决定不同的工程规模与排水效率，进而影响工程费用与作物产量效益。故本文选取排水历时、农沟间距、各级沟道断面底宽、沟深、边坡系数作为决策变量，优化排水沟系统，综合发挥其排水蓄涝、生态减污等效能。

图1 一条干沟控制的排水沟系统概化图Fig.1 A schematic diagram of a drain system controlled by a main ditch

1.1 目标函数

1.1.1 工程年费用子目标

年费用折算现值f是工程项目经济计算期内匹配某一除涝标准的土方开挖费K1、占地补偿费K2、生态边坡建造费K3组成的基础性设施投资与排水沟系统清淤、边坡维护等产生的年平均运行管理费C0之和，其中各项可由几何推导：

(1)

(2)

(3)

(4)

式中：P1i、P2i、P3i分别为i级排水沟挖方单价、占地单价、生态边坡建造单价，元/m；k为排水沟级数；Bi、mi、Hi、Zi、Li、di分别为i级排水沟底宽、边坡系数、沟深、总沟长、间距、沟带单宽，m，其中Zi经数据拟合可表示为既定项目区Li的相关函数Zi(Li)；α为排水沟系统运行管理费率。

经以上方法可得年费用折算现值最小的子目标为：

(5)

式中：ic为基准折现率；N为经济计算期即工程使用年限，a。

1.1.2 污染物去除量子目标

采用水环境研究中普遍应用的河流一级模型污染物衰减方程[15]预测其途经i级排水沟的浓度：

ci=c0e-r HRTi

(6)

HRTi=wi/qi

(7)

式中：c0为排水沟初始水体污染物浓度，mg/L；r为总体降解系数，d-1，是影响污染物浓度变化的直接影响因素，其值大小与排水沟生态措施相关，一般根据当地试验调查分析综合比较选定，南方稻作区排水沟降解系数一般为0.06～0.40 d-1[5，7，16]；HRTi为污染物通过第i级沟的水力停留时间，d；wi为所计算i级沟水体体积，m3；qi为平均排除法计算的i级沟排水流量，m3/s。

根据排水沟系统概化图，考虑同级排水沟断面尺寸、长度均相同，下级排水沟均匀间隔分布于上一级排水沟沿线，则污染物于农沟以面源形式汇入，于斗沟、支沟、干沟以点源形式汇入。据此可由下而上逐级递推得各级排水沟末端断面污染物浓度，其中干沟末端污染物浓度计算公式经推导可化简为：

(8)

(9)

式中：c为干沟末端断面污染物浓度，mg/L；c4为农沟末端断面污染物浓度，mg/L；v3、v2、v1为斗沟、支沟、干沟平均流速m/s，是平均排除法计算的排涝流量与断面面积的比值；R为设计径流深，mm；Fi为第i级排水沟控制的排水面积，km2；Ai为第i级排水沟断面面积，m2；l3、l2、l1为单条斗沟、支沟、干沟的对应沟长，m；I、J为单条干沟控制的支沟数量、单条支沟控制的斗沟数量，是由各级沟道规划长度间比例关系确定的常数；K为单条斗沟控制的农沟数量，是斗沟规划长度与决策变量中农沟间距的相关函数K(L4)。

由于初始排水时所有农沟污染物浓度相等，整个排水沟系统一次排水的污染物去除率η与去除量(M)最大的子目标可表示为：

η=1-c/c0

(10)

maxM=IJK(L4)q4[c(T,Bi,mi,Hi)-c0]T

(11)

1.1.3 作物相对产量子目标

将年平均降雨量转换为等量n次的设计暴雨量P，利用土壤饱和体积含水率θr等转化计算一次设计暴雨的地下水位上升值H，并假设地下水埋深在排水时间T内均匀降落，由此表示设计暴雨规模的相对产量年际变化。则雨后第j天(0≤j≤T)排水后的地下水埋深Xj为：

(12)

式中：H0为现状地下水埋深，cm；θ0为现状土壤体积含水率。

采用DRAINMOD模型[17]中总结作物同时受到涝渍影响产量变化的试验研究成果基础上基于Hiler提出的抑制天数指标概念(SDI)采用的公式，建立作物受涝渍后相对产量最高子目标：

(13)

式中：Ryw为作物受涝渍后可获得的相对产量，%；Rymax为作物可以忍受一定高水位条件而不减产的相对产量，可能大于1；CSwj为第j天作物对涝渍的敏感因子；Xj为第j天地下水埋深，cm，是关于决策变量排水历时的函数Xj(T)；当埋深大于30 cm时30-Xj值为0，表示作物不受涝；Rymax、CSwj的取值可根据实测资料线性拟合反推或采用DRAINMOD模型中自带的美国常见作物经验值。

1.2 约束条件

(1)排水沟输水能力约束。该约束确保基础排水功能，保障洪涝灾害时的农田作物产量与下游安全：

Qp≤Q

(14)

即第i级排水沟须满足:

(15)

式中：i为排水沟级数；Qp为平均排除法计算的排涝流量，m3/s；Q为排水沟过水能力，即允许通过的最大流量，m3/s；R为设计径流深，mm；Fi为第i级排水沟控制的排水面积，km2，农沟控制的排水面积F4是决策变量农沟间距的函数F4(L4)；n为沟道糙率；ii为i级排水沟坡降。

(2)边坡稳定约束。该约束以排水沟最小、最大边坡系数mmin、mmax保证工程安全稳定，避免塌坡等不利事故。即：

mmin≤mi≤mmax

(16)

(3)流速约束。根据当地土壤性质、植被类型、沟断面水力要素选择相应不冲流速以维持沟床稳定。即：

vi≤v不冲

(17)

式中：vi为第i级排水沟实际过流流速，m/s；v不冲为排水沟植被生长所允许的最大冲击流速，m/s。

(4)底宽约束。根据当地排水沟通航、养殖、滞涝等要求设置排水沟最小底宽(Bmin)。即：

Bi≥Bmn

(18)

(5)沟深约束。约束排水沟最小沟深(Hmin)以满足当地机耕和农作物对地下水位的要求等。即：

Hi≥Hmin

(19)

(6)排水农沟间距约束。即：

(20)

(7)相对产量约束。根据规划时允许的最低作物相对产量Rywmin设置约束以保障地区粮食供需平衡。即：

Ryw≥Rywmin

(21)

(8)污染物净化率约束。即：

η≥ηmin

(22)

式中：η为污染物净化率；ηmin为规划允许的最小污染物净化率。

(9)出水达标率约束。排水沟系统末端出水中某污染物浓度须满足承泄区水质功能区划水质标准，一般为适用农业的地表Ⅴ类水水质标准。即：

c≤cr

(23)

式中：c为干沟末端断面某污染物浓度，mg/L；cr为承泄区该污染物的水质标准限值，mg/L。

(10)农田系统水面率约束。为极大发挥排水沟系统生态湿地功能，将直接影响水质净化效果的湿地面积作为限制条件[18-20]。即：

ρ≥ρmin

(24)

式中：ρ为规划后农田系统实际水面率；ρmin为农田系统规划允许的最小水面率。

2 求解方法

2.1 设计思路

多目标优化问题的子目标之间是存在矛盾的，不可能存在一个解同时成为各子目标函数的最优解，寻求非劣解集是多目标决策的基本手段。本模型求解步骤分为以下2个部分：①在没有决策偏好信息，难以标量化处理成单目标优化问题直接衡量解的优劣性前提下，运用粒子群算法中每一代可行解间相互比较淘汰劣解逼近最终非劣解集的方法，获得排水沟系统规划的待选方案集。②针对待选方案集运用基于目标达成度的灰色关联投影法，科学优选出最终规划方案。

2.2 基于粒子群算法求解非劣解集

粒子群算法(PSO)[21]利用个体粒子i对信息的共享使规模为N的整个群体在D维目标搜索空间中按照规则[式(25)、式(26)]更新自己的速度Vi=(vi1,vi2,…,viD)和位置Xi=(xi1,xi2,…,xiD)，不断迭代寻优向自身历史最佳位置pbest=(pi1,pi2,…,piD)和群体历史最佳位置gbest=(g1,g2,…,gD)聚集，产生从无序到有序的演化，最终实现对候选解的进化。

vij(t+1)=ωvij(t)+c1r1(t) [pij(t)-xij(t)]+

c2r2(t) [pgi(t)-xij(t)]

(25)

xij(t+1)=xij(t)+vij(t+1)

(26)

式中：vij是粒子的速度，并由用户设定±vmax限制粒子速度；pij(t)、pgi(t)分别为t时刻粒子的自身最好位置pbest和全局最好位置gbest；c1和c2为学习因子调节pbest、gbest方向飞行的最大步长；r1和r2为[0，1]范围内增加粒子飞行随机性的均匀随机数；ω是决定全局探索新方向好解和局部搜索原先轨迹好解能力的惯性权重。

运用粒子群算法优化排水沟系统多目标规划模型中的变量Bi、mi、Hi、L4、T，设置一定规模粒子群在多维空间随机搜索，以获得待选方案的非劣解集。

2.3 基于目标达成度的灰色关联投影法优选非劣解集

针对粒子群算法优化所得待选方案非劣解集运用基于目标达成度的灰色关联投影法[22](GRA)进行多目标决策，具体步骤如下。

(1)确定模型3个子目标的期望水平值与可接受最劣值，取各子目标期望水平值与可接受最劣值之差作为相对最佳决策方案A0，并与非劣解集中N个待选方案构成增广型矩阵[Ai,j](N+1)×3(i=0,1,2,…,N；j=1,2,3)。

(27)

(3)计算非劣解集方案与相对最佳方案的灰色关联度rij，构造灰色关联度判断矩阵[Pi,j](N+1)×3：

(28)

通常情况下，取λ=0.5。

(4)设置3个子目标间加权向量W=[W1,W2,W3]T>0，对灰色关联度判断矩阵加权处理得灰色关联度决策矩阵P′(WjPi,j)(N+1)×3。

最后，将非劣解集待选方案看成行向量，计算与相对最佳方案之间的灰色关联投影角，综合考虑夹角余弦值与模的大小，计算灰色关联投影值Di进行科学排序，决策多目标最优方案。即：

(29)

3 实例应用

3.1 项目区概况

上海松江区高标准农田区地处亚热带北缘，光、热、水同季，多年平均蒸发量1 252 mm，多年平均降雨量1 117.1 mm，汛期平均暴雨量大于90 mm/d。规划区域面积1 120.7 hm2，高程在3.3 m左右；土壤类型介于粉砂土与中壤土之间；潜水水位埋深一般为0.5～1.5 m；现状种植品种以“秀水114”、“秀水134”常规水稻为主，近年的平均产量最高可达8 610 kg/hm2。

3.2 模型数据

根据上海市《粮田和菜地水利基础设施建设技术规范》(DB31/T 469-2009)规定，以20 a一遇最大设计24 h面雨量180.2 mm排至地面以下0.6 m为标准，应用多目标模型规划2级排水沟系统。根据项目区地形图研究测算排水农沟间距与总长进行数据拟合，得排水农沟总长与间距函数关系l=302 038L-1.049(R2=0.993 9)。将项目区现状农田坡降0.000 5、糙率0.030、水田滞蓄水深40 mm、不透水层埋深6 m、土壤渗透系数0.39 m/d、土壤给水度0.04、排水沟总氮(TN)初始浓度6 mg/L、TN总体降解系数0.3～0.4 d-1(根据当地试验调查分析，综合比较选定)输入模型；依据工程30 a规划运行年限及当地经济情况确定挖方单价、占地单价、生态边坡建造单价分别为15、25、20 元/m、运行管理费率为2%、作物受涝渍后相对产量允许下限值为85%。

采用MATLAB实现编程和界面可视化，参考相关文献[23]对影响算法性能和效率的控制参数设置如下：种群规模N=500，惯性权重ω=0.8，加速系数c1=c2=0.3，非劣解集规模上限为120，迭代次数为80。

3.3 结果与分析

非劣解集中的各方案是各决策变量(T、Hi、Li、Bi、mi)不同的取值组合，每一方案的取值组合对应该方案的3个子目标预期值。各决策变量间地位等同，无主次顺序，非劣解集中的各方案无排序依据。考虑决策变量中的排水历时是连续小区间内有限个数的离散整数形式，且构建的作物产量子目标是排水历时的函数，即同一排水历时的作物相对产量相等，先按照排水历时将非劣解集方案分类汇总，粒子群优化过程见图2、图3，再分别按照年费用子目标预期值大小与去污量子目标预期值大小进行非劣解集中方案的排序，结果一致。不同排水历时的所有待选方案单位年费用与TN去除量效果见图4。

图2 年费用子目标优化过程Fig.2 Optimization process of annual cost sub-goal

图3 TN去除量子目标优化过程Fig.3 Optimization process of TN removal sub-goal

由不同排水历时的年费用与TN去除量关系图可知，随着排水历时增加，相同年费用下的TN去除效果更明显，而要达到相同的TN去除量，年费用与排水历时呈负相关关系；同一排水历时的年费用随TN去除量增大而增加，且增长速率逐渐增加。

针对某一排水历时的粒子群算法所求规划方案非劣解集，将相对产量目标值按照项目区最高年产量与市场水稻单价换算为减产折算费用(见图5)，根据费用效益比优选该排水历时的优选方案，再对各排水历时的优选方案根据费用效益比优选出最优排水历时的最优规划方案。不同排水历时下的优选方案见表1，传统单目标方案与模型多目标方案及效益对比见表2。

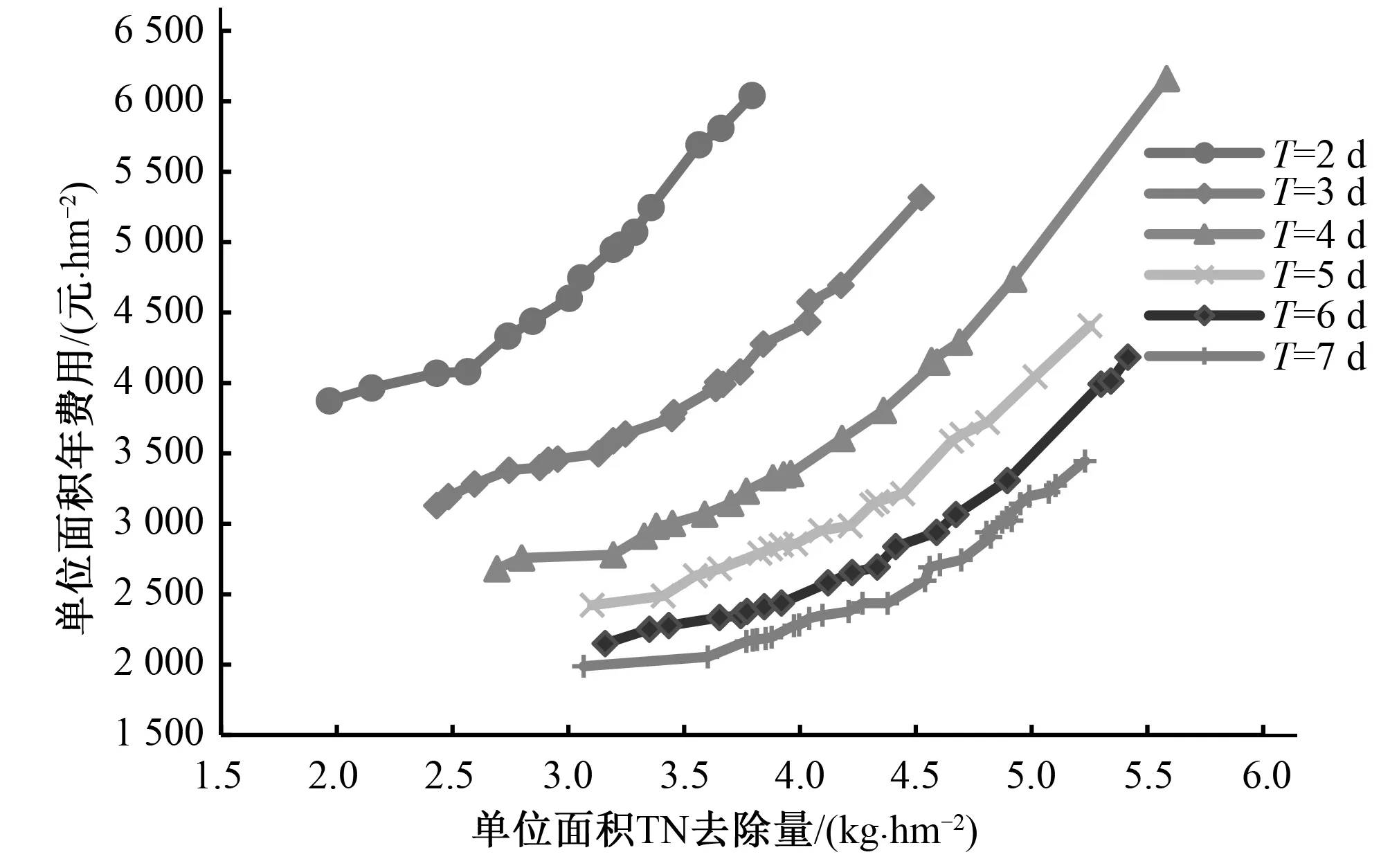
图4 不同排水历时下各方案单位年费用与TN去除量效果Fig4. The annual cost and TN removal efficiency of each programme unit under different drainage time

图5 排水历时为5 d的方案效果Fig.5 Scheme effect under 5 d drainage time

表1 不同排水历时下的优选方案Tab.1 Different drainage diachronic optimization schemes

表2 传统单目标方案与模型多目标方案及效应对比Tab.2 Effect comparison of traditional single target scheme and multi-objective model scheme

采用基于目标达成度灰色关联法分析，确定不同排水历时的优选方案(见表1)。根据不同排水历时的优选方案灰色关联投影值排序，确定4号方案为本项目区最优规划方案，其结果与通过费用效益比优选的最优方案一致。即按照排水历时5 d，排水农沟与支沟深1.3、1.7 m，间距77、270 m，规划设计排水沟,预期优化水面率7.64%，增加滞涝水量648.5 m3/hm2,同时稻作区单位面积的TN削减能力约为4.22 kg/hm2，TN削减率约达59.8%，比传统单目标规划方案的TN削减能力增加了1.81 kg/hm2，TN削减率增加了28.1%，水稻相对产量96.2%，年费用不变。

4 结 论

本文基于工程年费用、污染物去除量、作物相对产量3个子目标构建排水沟系统多目标规划模型，利用粒子群算法耦合灰色关联投影法决策最优规划方案。主要结论如下。

(1)本模型运用粒子群算法耦合灰色关联投影分析法,综合权衡多目标间的矛盾性，在确保产量效益与年费用投资合理的前提下，通过稻作区滞涝减排换取生态减污效益，实现排水沟系统的最优规划，模型是合理可行的。

(2)运用粒子群算法实现问题转换并客观提供多目标非劣解集进行灰色关联投影分析，实现多目标决策，这种基于PSO-GRA处理复杂的非线性多目标优化规划问题的求解方法是有效的。

(3)将模型应用于上海松江区高标准农田稻作区排水沟规划，优化水面率7.64%，可增加滞涝水量648.5 m3/hm2,单位面积TN削减能力比传统单目标规划方案约增加1.81 kg/hm2,削减率约增加28.1%，为南方稻作区的排水系统节水减排规划建设工程提供了参考。

□