基于双参数Gumbel-Hougaard Copula函数的 设计洪水地区组成分析

牟时宇，石 朋,2，赵兰兰，崔彦萍，冯 颖，董丰成，陈 琛

(1.河海大学水文水资源学院，南京 210098；2.水文水资源与水利工程科学国家重点实验室，南京 210098； 3.水利部信息中心，北京 100053；4.江苏省水文水资源勘测局，南京 210029)

洪水地区组成是研究流域开发方案，上下游、干支流工程联合调洪运行时需要分析的问题。传统分析方法有地区组成法、频率组合法、随机模拟法[1]。前2者的共同缺点是难以理清各个分区洪水组成的概率问题，主观假定可能的组成方案而削弱了洪水的空间相关性[2]。而随机模拟法难以掌握模拟序列统计特征的稳定性。近年来，Copula函数在水文上的应用[3,4]为设计洪水地区组成研究提供了突破口。Copula函数可以灵活地构建任意多个变量之间的联合分布函数，模拟变量间非线性关系的性质使推求更加合理的地区组成成为可能[5-7]。

然而，目前设计地区洪水组成的研究均选取单参数的Gumbel-Hougaard Copula函数(以下简称GH Copula)作为联合分布函数的载体，其拟合效果受系列长短的影响较大，参数估计结果具有较大的不确定性。而多参数GH Copula函数保留了单参数GH Copula函数的上尾相关性，且因参数个数的增加，使函数结构更加灵活，能够更好地反映极值事件的相关性。本文基于多参数GH Copula函数分别运用条件期望组合法、条件最可能组合法、最可能组合法、同频率组成法拟定淮河流域中渡断面的设计洪水地区组成方案。淮河中上游大型水库、闸坝众多，分析该区间段设计洪水地区组成对淮河流域综合治理有重要意义。

1 研究方法

1.1 Copula函数模型

1.1.1 GH Copula函数

水文上常用的GH Copula为单参数Copula函数，其数学表达式如下：

C(u,v;θ)=exp {-[(-logu)θ+(-logv)θ1/θ}

(1)

式中：θ为参数并且满足θ≥1。

GH Copula的上尾相关系数为2-21/θ，是Archimedean Copula中唯一可以用于多变量极值分析的Copula函数，适合刻画具有上尾相关性的水文变量。

通过对生成元φ0(t)=(1/t)-1增加内外幂的方式可以构造双参数GH Copula函数[8]：

C(u,v;β1,β2)={[(u-β2-1)β1+(v-β2-1)β1]1/β2+1}-1/β2

(2)

式中：β1、β2为参数，并且满足β1≥1，β2>0，其中β2是与下尾相关性有关的参数。

双参数GH Copula函数更具灵活性和外延性，对于相关性一般的变量而言更具优势。

在单参数GH Copula函数的基础上引入了Marshall-Olkin Copula函数可构造三参数GH Copula函数[9]：

C(u,v;θ,π2,π3)=exp [-A(-logu,-logv;θ,π2,π3)]

(3)

A(x,y;θ,π2,π3)=

[(π2x)θ+(π3y)θ]1/θ+(1-π2)x+(1-π3)y

(4)

式中：θ≥1，0≤π2,π3≤1。

其尾部相关系数与单参数GH Copula函数相同。三参数GH Copula函数是非对称Copula函数，用于拟合概率分布具有非对称性的二维变量。

1.1.2 Copula函数的拟合优度评价

Copula函数的拟合优度评价分为3类方法：

(1)利用离差平方和(OLS)最小准则、AIC准则从整体上评价Copula函数拟合效果：

(5)

(6)

AIC=nlnMSE+2m

(7)

式中：Femp(xi,yi)为经验频率；C(ui,vi)为理论频率；m为模型参数的个数。

(2)通过绘制图形的方法直观比较Copula函数拟合效果：包括Genest和Rivest[10]提出的图形法，即绘制 Copula函数的理论估计与经验估计的Q～Q图；Salvadori[11]提出的Pickland's依赖函数法，对比经验与参数Copula的Pickland's依赖函数曲线，该方法也被用于多参数Copula函数的参数估计。

(3)除了从整体上评价Copula函数的拟合效果外，还应考虑选取的Copula函数能否反映极值事件的相关性。上尾部相关系数是衡量极大值事件发生时变量间的相关程度，CFG[12]为其常用的估计算法：

(8)

式中：(Ui,Vi)是根据实测点据获得的第i组随机样本。

1.2 设计洪水地区组成计算方法

当下游断面发生设计洪水zp时，上游断面洪量X与下游区间洪量Y有无穷多种组合情况，下面给出3种具有代表性[5,7]的地区组成计算方法。

1.2.1 条件期望组合

将上游断面洪量X取xp，将下游区间洪量Y取期望值E(y|xp)，所形成的组合(xp,E(y|xp))记为条件期望组合[5]。E(y|xp)通过下式进行计算：

(9)

f(Y≤y|X=xp)=c(u,v)fY(y)

1.2.2 条件最可能组合

当上游断面洪量X取设计洪量xp时，下游区间洪量Y取使f(Y≤y|X=xp)达到最大值时对应的yM值，将(xp,yM)记为条件最可能组合。f(Y≤y|X=xp)对y求导得：

(10)

c2=∂c/∂v

令df(Y≤y|X=xp)/dy=0，整理得：

(11)

一是评先评优有倾斜。对回乡创业贡献突出的能人，优先提名为党代表、人大代表、政协委员候选人，优先安排参加劳动模范、优秀企业家等各类荣誉评选。二是授予特殊荣誉。对不担任镇村职务的回乡能人，可以探索设立“新乡贤”“荣誉村民”“先锋党员”等称号，充分尊重其社会表现，给于其荣誉地位，引导社会尊重他们。三是给予适当政治待遇。对表现较好的未担任镇村职务的回乡能人，可以安排其作为特别会议代表，列席一定范围的镇村党务政务会议，可以在重要节庆活动时由组织进行走访慰问。

当y的边缘分布函数为P-Ⅲ型分布时，fY(y)的表达式如下：

(12)

式中：α、β、γ分别为位置参数、尺度参数、形状参数。

将式(12)代入式(11)中，可推导边缘分布为P-Ⅲ型分布的二维条件最可能组合法计算通式：

(13)

通过牛顿迭代法对非线性方程式(13)求解，即可得到条件最可能组合(xp,yM)。

上游断面洪量X取值为xp时，分别令F(Y≤y|X=xp)等于α/2和1-α/2，求得对应的下游区间洪量Y的值分别为yL和yU，称[yL,yU]为xp对应的Y的置信区间。洪量置信区间可以定量评价设计洪水地区组成估计值的不确定性，为决策人员明晰决策风险提供了依据[13]。条件最可能组合与条件期望组合并称为条件地区组成法。

1.2.3 最可能组合

当下游断面发生设计洪水zp时，上游断面洪量X与下游区间洪量Y存在一个最可能组合，即求解在X+Y=zp等式约束条件下X与Y联合分布概率密度函数f(x,y)的最大值。利用牛顿迭代法对非线性方程式(14)求解，即可得到最可能组合(x,zp-x)。

(14)

c1=∂c/∂u，c2=∂c/∂v

式中：αx、βx、γx，αy、βy、γy分别为FX(x)、FT(y)对应的参数。

2 应用实例

选择淮河干流中渡断面以上流域作为研究区域(见图1)。中渡站位于洪泽湖出口处，是淮河中游总控制站，控制流域面积15.82 万km2。淮河中游按河道特性和地形起伏分为鲁台子以上和以下2个区间段，鲁台子以上流域面积8.86 万km2；鲁台子至中渡段河长335 km，区间控制面积6.96 万km2。本文以鲁台子断面为界，研究其上和其下2个区间段的洪水对中渡断面的设计洪水组成的贡献率。

图1 中渡断面控制水系示意图Fig.1 Sketch map of drainage of Zhongdu site

选用1951-2010年鲁台子站和中渡站洪水的同步观测资料及1931年实测大洪水资料，将流域内的大型水库、湖洼、行蓄洪区的拦蓄水量、灌溉引用水量等演算至鲁台子、中渡断面，并与断面实测流量过程相加得到该断面天然流量过程，根据淮河流域的洪水特点及水利工程的调节特性，选择设计洪量控制时段为30 d[1]。绘制历年鲁台子、中渡站天然年最大30 d洪量W30时历曲线及模比系数累积平均值曲线[14](见图2)，系列中较好的包含了丰、平、枯的完整过程且在45 a以上具有较强稳定性。鲁台子和中渡(以下简称鲁中)区间洪水资料采用中渡控制断面的天然洪水过程扣除鲁台子控制断面错开传播时间演算的天然洪水过程，求得区间洪水过程后再统计各时段洪量。

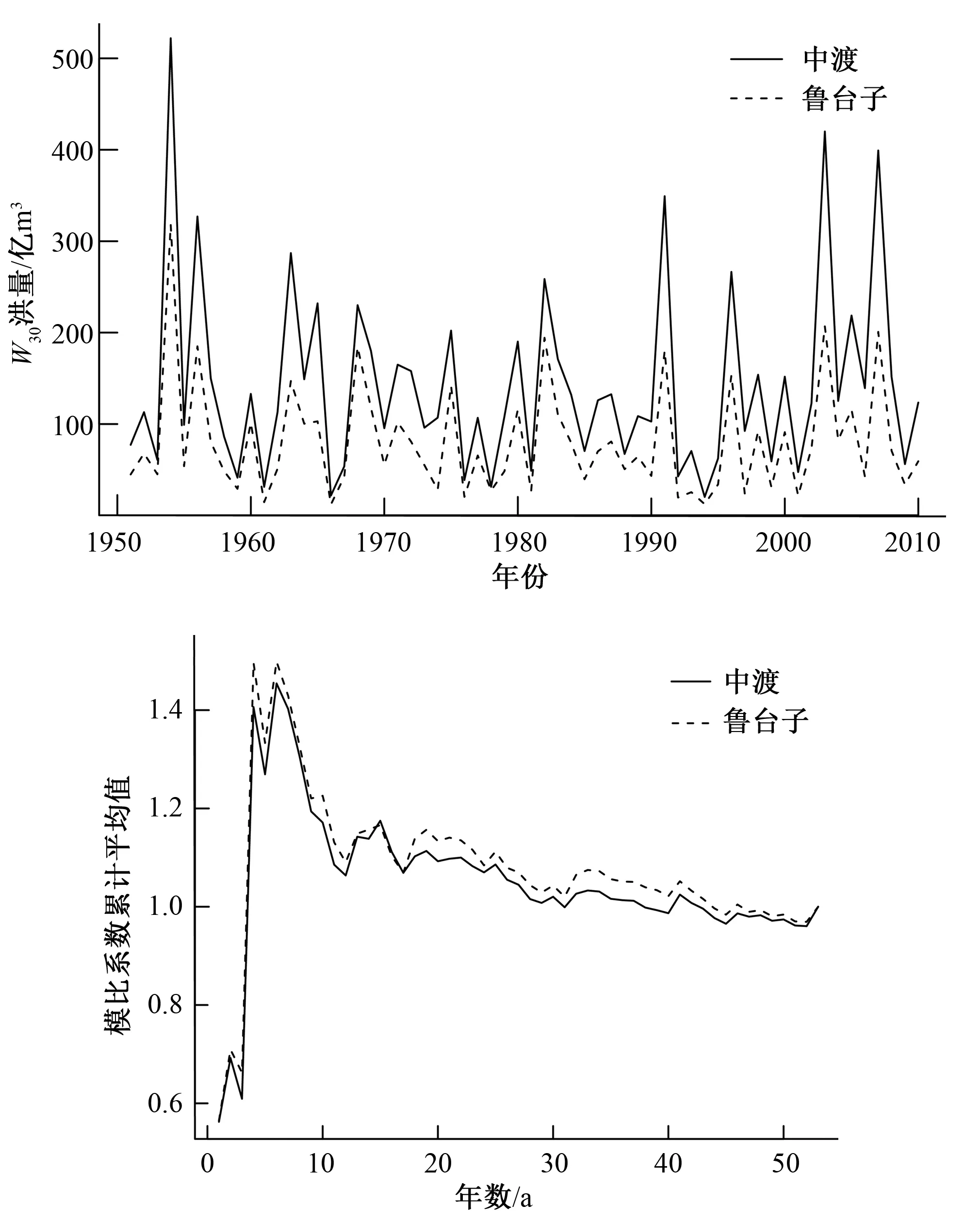
图2 鲁台子、中渡断面W30时历曲线及模比系数累积平均值曲线Fig.2 Time history and cumulative average modulus coefficient curve of W30 at Lutaizi and Zhongdu site

2.1 边缘分布的确定

各区W30服从P-Ⅲ型分布，将1931年、1954年作为大洪水年，其洪量按1915年以来排位处理，采用统一处理法计算不连续样本频率，运用计算机优化适线法估计E(X)、Cv、Cs，并将其转化为P-Ⅲ型分布的位置参数α、尺度参数β、形状参数γ，其转换关系如式(15)。最终参数估计结果如表1所示。

(15)

表1 各分区P-Ⅲ分布参数估计结果Tab.1 Parameter estimation results for P-Ⅲ distribution of each region

2.2 联合分布函数的确定

基于单参数、双参数、三参数GH Copula函数构建鲁台子W30与鲁中区间W30的联合分布函数。采用极大似然法估计3种GH Copula函数的参数，利用OLS、AIC准则来优选GH Copula函数，参数估计结果及对应拟合优度指标列于表2。分别绘制3种GH Copula函数的Q～Q关系图(见图3)；计算经验Pickland's依赖函数与运用3种GH Copula函数分别生成1 000个随机模拟点估算的Pickland's依赖函数，并画图对比(见图4)。此外，用CFG法估计实测点据的上尾相关系数为0.636。

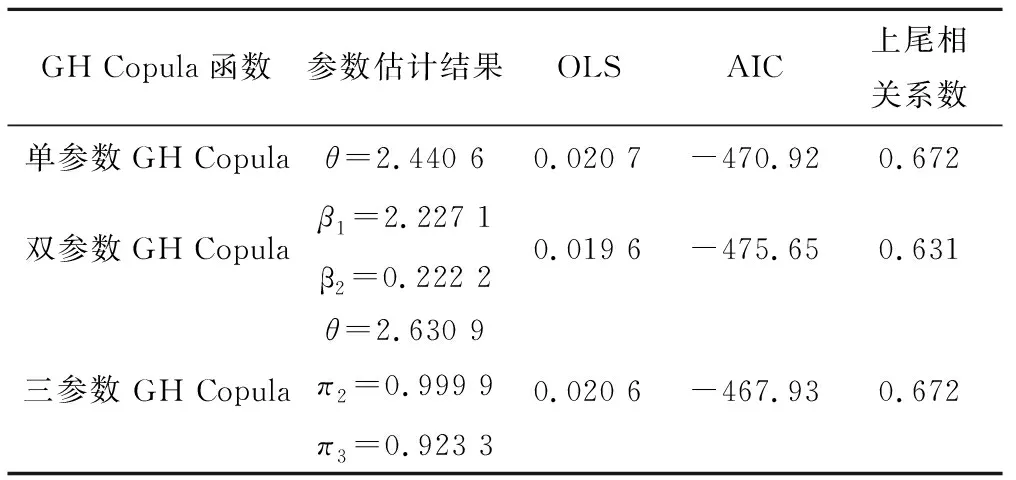
表2 3种GH Copula函数参数估计结果及拟合优度指标Tab.2 The estimated parameters and goodness of fit of three GH Copula Functions

图3 鲁台子W30与鲁中区间W30联合分布的理论估计与经验估计关系Fig.3 The theoretical and empirical distribution for joint distribution of W30 at Lutaizi and Luzhong interval

图4 基于鲁台子W30与鲁中区间W30的 经验与拟合Pickland's依赖函数关系Fig.4 Plots of empirical and fitted Pickland's dependence functions of W30 at Lutaizi and Luzhong interval

从表2可以看出，双参数GH Copula函数对应的OLS、AIC值最小，上尾相关系数估计值与样本估计值最为接近，拟合效果最优。图3中3种Copula函数的点据均落在45°线附近；图4中双参数GH Copula拟合的Pickland's依赖函数的曲线与经验值最为接近，近乎重合。综上，选取双参数GH Copula作为构造鲁台子W30与鲁中区间W30联合分布的连接函数。

3 结果与分析

3.1 条件地区洪水组成

条件地区洪量组成考虑的是上游断面与区间洪量的空间相关性。其中，条件期望组成强调的是在所有可能出现的洪水地区组合方案中的平均水平，可作为洪水分配方案参考；条件最可能组成则强调实测组合更具备出现的可能性，是一种条件最优分配方案。本实例计算了分别以鲁台子W30、鲁中区间W30为条件，另一分区相应W30的条件地区洪量组成，并与工程上常用的同频率组合法进行对比分析(见图5)。

图5 中渡站W30 3种地区组成关系Fig.5 Comparison for three regional flood composition

图5(a)给出了以鲁台子W30为条件，鲁中区间相应的W30估计值(条件期望组成I、条件最可能组成I、同频率组成I)及其90%的置信区间。4种设计洪水地区组成方案估计值均在90%置信区间内。以条件期望值I作为比较标准，条件最可能组成I以上游设计频率为40%为界，当频率高于40%时，其估计值高于条件期望值；反之，其估计值低于条件期望值。而对于同频率组成I，当设计频率高于10%时，其估计值随设计标准的提高逐渐向下偏离条件期望值。淮河中游区5～20 a一遇的中小洪水事件发生频繁，是防范洪灾风险中更应该关注的问题。根据图5(a)分析结果，对于该频率段洪水，同频率组成I方案有可能使下游断面达不到预期的防洪标准；与之相反，条件最可能组成Ⅰ则提供了一种“对防洪不利”的偏安全的组成方案。

图5(b)给出了以鲁中区间W30为条件，鲁台子相应的W30估计值(条件期望组成Ⅱ、条件最可能组成Ⅱ、同频率组成Ⅱ)及其90%的置信区间。4种设计洪水地区组成方案估计值均在90%置信区间内。以条件期望值Ⅱ作为比较标准，条件最可能组成Ⅱ以区间W30设计频率为42%为界，当频率高于42%时，其估计值高于条件期望值；反之，其估计值低于条件期望值。同频率组成值II与条件期望值接近。对于5～20 a一遇的中小洪水，3种方案计算的结果相近。但当发生设计频率低于3%的极值洪水事件时，同频率地区组成计算结果处于一个较低的保证率水平，难以保证下游中渡断面的防洪安全。

3.2 最可能地区洪量组成

最可能地区组成法是从自然规律的角度出发，按照下游防洪标准设定的一种最优分配方案。表3列出了最可能组成法分配结果，同时对比条件洪水组成法、同频率组成法估计结果。最可能组成结果位于条件期望组成Ⅰ、Ⅱ，条件最可能组成Ⅰ、Ⅱ，同频率组成Ⅰ、Ⅱ之间。当中渡断面发生5～20 a一遇的设计洪水时，若按最可能组成法进行分配，上游鲁台子断面及鲁中区间均发生低于该频率段的设计洪水，2分区发生了洪水遭遇是造成中渡断面高频洪水的主要原因。

表3 中渡断面设计洪水地区组成计算结果对比 亿m3

3.3 设计洪水地区组成方法计算贡献率对比

鲁台子站控制面积占中渡站控制面积的56%，而根据实测资料统计其洪水来量占中渡站洪水总量的60%以上，是淮河中上游主要的汇水区。计算综上所有洪水分配方案在不同量级情景下上游设计洪量对中渡设计洪量的贡献率，相应区间贡献率也可经简单计算得到，见图6。从图6可以看出在设计频率高于20%时，条件期望组成II、条件最可能组成II、同频率组成II计算的贡献率存在小于56%的情况，与实际水量分配不符，不宜选择此3种方案。同频率组成I计算的贡献值随设计频率变化的幅度很大，且在高频段计算的贡献值偏离其他分配方案结果，容易低估区间洪水风险，具有明显的不合理性。设计洪水地区组成的任务是在下游断面发生设计洪水条件下，拟定不同种洪水组成方案，使得按其确定的水库防洪设计指标及调洪规划在水利工程运行中能够使下游断面达到预期的防洪标准。条件最可能组成I随频率变化幅度较小，计算结果稳定，可作为确定水库防洪设计指标的依据。条件期望组成I与最可能组成计算的贡献率随设计频率的增大均存在上升趋势，且变化规律一致。最可能组成计算的区间洪量的贡献率最大，为中渡断面W30设计洪水组成提供了对防洪最为不利的组成方案，可供水库常规调度参考。

图6 不同量级情景下鲁台子设计洪水的贡献率Fig.6 Contribution rate of Lutaizi design flood under different magnitude scenarios

4 结 论

以淮河中游控制站中渡站为例，基于双参数GH Copula函数，构造鲁台子断面、鲁中区间最大30 d洪量的联合分布函数并对比分析条件期望组成、条件最可能组成、最可能组成及同频率组成4种设计洪水地区组成分配方案的适用性，得到以下结论。

(1)双参数GH Copula函数与单参数GH Copula函数相比结构更加灵活，能够更好地考虑各区洪水的相依性结构。

(2)条件期望组成代表各种组成方案的平均水平，具有统计基础和参考意义。条件最可能组成是一种条件最优分配方案；最可能组成是一种按照下游防洪标准设定的最优分配方案，可为防洪规划提供合理的边界参考。同频率组成法人为地将存在相关性的上下游洪量分隔开来，再硬性组合，计算结果处于较低保证率水平。

(3)上述4种地区组成的方法都是以单项特定的地区组成情况去概括所有可能出现的多种多样的组合，计算的洪水贡献率存在较大差别。对于中渡断面而言，从洪泽湖的安全及设计合理性的角度出发应选择最可能组成分配方案作为设计参考。

□