潮流能水平轴水轮机叶片扭角与弦长分布研究❋
王树杰, 王宽宽, 袁 鹏, 于晓丽, 王旭超
(1. 中国海洋大学工程学院,山东 青岛 266100; 2. 海洋工程山东省重点实验室,山东 青岛 266100)
潮流能是潮汐现象引起的海洋水流具有的动能,流向具有可预测性,易于能量转换。潮流能发电装置由获能装备、载体与支撑结构组成,潮流能水平轴水轮机是一种获能系数较高的潮流能获能装备,它是利用潮流水流流过其叶片产生的升力,推动水轮机转子绕其轴线旋转做功,水轮机转子连接发电机,将潮流能转化为电能[1-2]。
叶片是水轮机的关键部件,决定着水轮机的获能效率与所受载荷情况,继而决定着水轮机的发电功率以及对载体与支撑结构的强度、抗倾覆、抗滑移要求。载体与支撑结构以水轮机所受载荷为依据设计制造,其造价占整个工程较大比重,因此,在满足获能效率的前提下,尽量减小水轮机所受载荷很有意义。叶片的翼型、半径、扭角、弦长等决定着叶片的外形,其中,扭角与弦长是叶片的主要设计参数,国内外普遍采用Glauert模型及考虑轮毂与叶尖损失的Wilson模型计算扭角与弦长分布[3-6]。由于水和空气介质物理特性的相似性,水轮机与风力机原理也具有相似性,国内对风力机的优化研究较多,汕头大学刘雄等考虑风场风速概率分布,以风力机年能量输出最大为目标,使用遗传算法对叶片优化设计[7];重庆大学陈进等以风力机的单位输出成本为优化设计目标对叶片进行设计[8];西北工业大学邓磊等基于响应面的方法,以功率系数与年发电量最大为目标对叶片优化设计[9];这些优化设计主要是对叶片扭角、弦长分布的优化。在借鉴风力机叶片优化研究的基础上,针对潮流能流密度高,水轮机承受载荷大的特点,研究水轮机叶片扭角与弦长分布情况。
本文以国家海洋可再生能源专项资金项目“轴流式潮流能发电装置研究与试验”中水轮机为研究对象,研究叶片扭角与弦长分布对水轮机转矩与轴向力的影响。水轮机转矩决定着水轮机功率,轴向力是水轮机所受主要载荷,以转矩满足发电功率要求,尽量减小轴向力为目标对水轮机叶片进行设计和修正,从而减少载体与支撑结构造价,降低发电装置海上施工难度,提高水轮机综合性能,保证发电装置的可靠性、稳定性,安全性要求。最后将扭角与弦长分布模型应用于潮流能水平轴水轮机设计软件中,使水轮机设计更加高效。
1 扭角与弦长的理想模型
潮流能水平轴水轮机叶片设计中,选取叶片上有限截面,即叶素(见图1),o为水轮机旋转中心,Ω为水轮机旋转角速度,RHub为水轮机轮毂半径,R为水轮机转子半径,r为叶片上某一叶素距旋转中心的距离。确定有限叶素的扭角、弦长数据,叶素与叶素之间区域可过渡产生,所有叶素集合即为叶片。
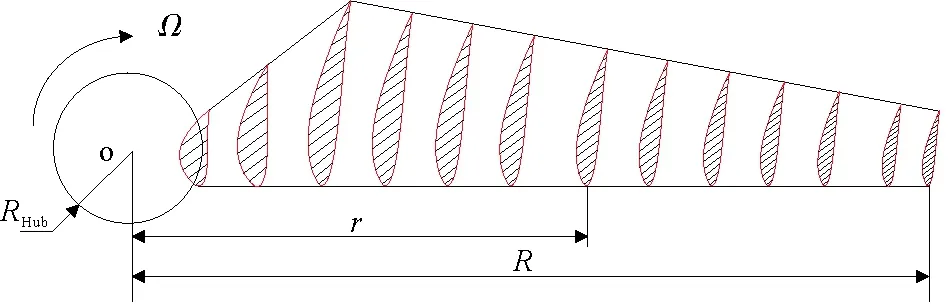
图1 叶片示意图Fig.1 Blade schematic
1.1 基本理论
水流流过水轮机,升力效应使水轮机旋转做功,水流轴向速度减小,并产生切向旋转速度,定义a、b分别为轴向诱导因子、切向诱导因子,用以表示水流轴向与切向速度的变化量,在稳态运行的情况下,a,b存在稳定值[10]:
(1)
式中:λ为局部速度比,表示距旋转中心r处叶素的线速度与水流速度之比,其中,叶尖处速度比为尖速比λ0,是水轮机的重要设计参数,且有:
(2)
选取叶片上距离旋转中心r处的某一叶素进行研究,叶素上速度与受力见图2,虚线为叶片叶素所在旋转平面,V为来流速度,U为水流相对于叶素的合成来流速度,合成来流速度U与旋转平面、弦长线的夹角分别为入流角φ、攻角α,旋转平面与弦长线的夹角为叶素的扭角β,叶素前缘到尾缘的最大距离为叶素的弦长c。
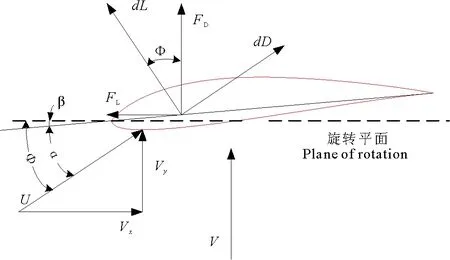
图2 叶素速度与受力图Fig.2 Blade element velocity and load diagram
合成来流速度U为平行于旋转平面的切向速度Vx与垂直于旋转平面的法向速度Vy的合成速度,并有[11]:
Vy=(1-a)V=Usinf,
(3)
Vx=(1+b)Wr=Ucosf。
(4)
根据库塔茹可夫斯基升力方程,推导叶素微元的升阻力为:
(5)
(6)
为使单个叶素效率最大,即dF/dD最大,由(5)、(6)式推导,得:
(7)
由(7)式可知,当叶素的升力系数比阻力系数即升阻比最大时,叶素的效率最大。叶素的升力系数、阻力系数取决于叶素选用的翼型、雷诺数、翼型的攻角。选用翼型已定时,升阻比最大时的攻角,为翼型的最佳攻角,即叶素的理想攻角。在一定工况雷诺数下,升阻力系数可通过开源软件XFOIL获得,最佳攻角通过攻角区间的升力系数、阻力系数的极坐标求得,CD-CL极坐标中斜率最大处对应的攻角即为最佳攻角αB(见图3)。
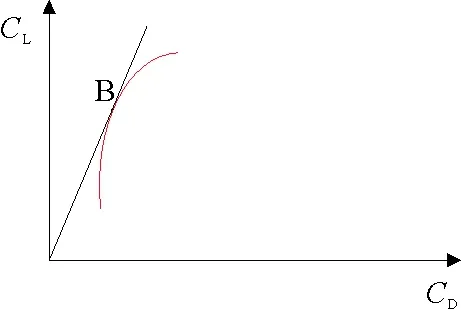
图3 CD-CL极坐标Fig.3 CD-CL polar coordinates
1.2 理想扭角分布
理想扭角为叶素效率最大时的扭角,有限叶素理想扭角构成扭角的理想分布。
由(2)、(3)、(4)式可得,叶片上距离旋转中心r处叶素的入流角φ为:
(8)
将稳态运行时的轴向诱导因子与切向诱导因子代入计算,即(1)、(2)式代入(8)式,得:
(9)
则距旋转中心r处叶素的理想扭角βB为:
(10)
式中:αB、βB计算时为弧度制值。
由(10)式可知,理想扭角是关于尖速比λ0、转子半径R、距旋转中心距离r、最佳攻角αB的函数,表示叶片设计中扭角大小由这些参数决定。
由(2)式可知,设计尖速比决定了水轮机的额定转速,并且尖速比与水轮机的额定转速存在正比关系,研究尖速比与理想扭角的关系对叶片设计中扭角取值具有指导作用。
以研究广泛的NACA4415翼型为例[12],在翼型分析软件XFOIL中得到,水轮机正常运转、雷诺数为1.5×106下最佳攻角αB为5.5°,转子半径R取为单位1,根据(10)式可得不同尖速比λ0下的理想扭角分布(见图4)。
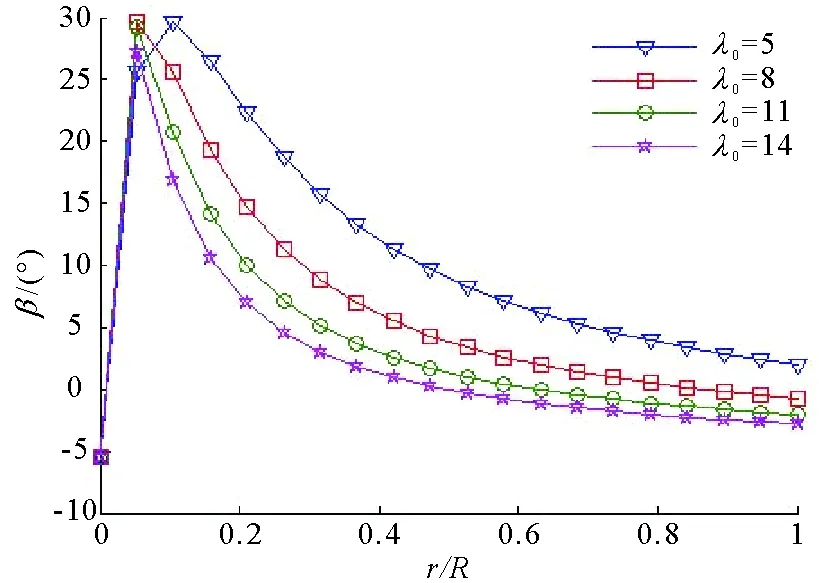
图4 不同尖速比下的理想扭角分布Fig.4 The ideal twist angle distribution under different tip-speed ratio
由图4不同尖速比下理想扭角分布可知,尖速比取值较大时,扭角值较小分布在叶片展长上,即水轮机额定转速取值较大,相应的叶片上叶素扭角的理想值就较小。
1.3 理想弦长分布
根据动量理论,叶轮轴向力T和转矩M等于单位时间内通过叶轮的流体动量和角动量的变化量。对于r处叶素微元dr的轴向力dT和转矩dM为:
dT=4prV2a(1-a)rdr,
(11)
dM=4pVW(1-a)br3dr。
(12)
根据叶素理论,若叶片个数为B,叶素r处宽度为dr的叶轮圆环上轴向力dT和转矩dM则可以表示为:
(13)
(14)
联立动量理论、叶素理论的计算结果,可得:
(15)
把(1)、(9)式,代入(15)式,可得弦长的理想值:
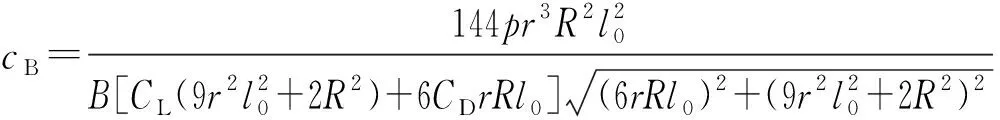
(16)
式中:CL、CD为相应工况雷诺数下,最佳攻角下的升、阻力系数。
由(16)式可知,理想弦长是关于尖速比λ0、转子半径R、距旋转中心距离r、叶片数B及最佳攻角下的升力系数CL、阻力系数CD的函数。
同上选取NACA4415翼型,水轮机正常运转、雷诺数为1.5×106下最佳攻角为5.5°,5.5°攻角下升力系数CL为1.084 7,阻力系数CD为0.008 2,叶片的个数B取为3,转子半径R取为单位1,根据(16)式可得不同尖速比λ0下的理想弦长分布(见图5)。
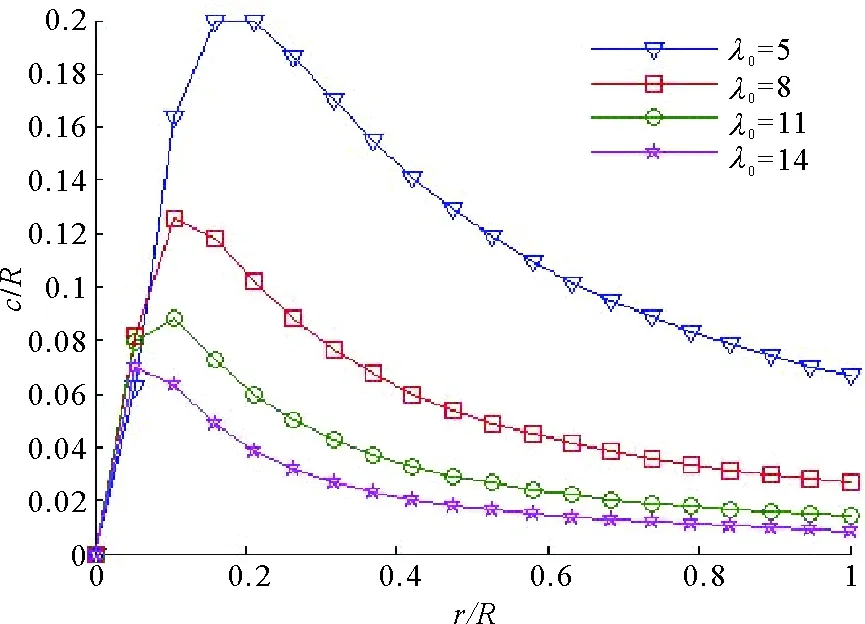
图5 不同尖速比下的理想弦长分布Fig.5 The ideal chord length distribution under different tip-speed ratio
由图5不同尖速比下理想弦长分布可知,尖速比取值较大时,弦长值较小分布在叶片展长上,即水轮机额定转速取值较大,相应的叶片上叶素弦长的理想值就较小。
2 扭角与弦长的修正模型
在实际的水轮机设计中,靠近水轮机旋转中心约10%R的区域内为水轮机轮毂,因此实际叶片设计中,理想扭角与弦长分布曲线前段10%R区域不予考虑,前段10%R~20%R区域为轮毂与叶片连接过渡区域[13]。
理论上,水轮机获能源于切向力相对水轮机旋转中心的转矩,由于叶片远段位置的力矩、切向力大,在叶片远段1/3区域为高获能区域,是叶片的主要获能区域,而在叶片近段1/3区域为低获能区域[9]。因此考虑修正叶片低获能区域扭角、弦长值,减小水轮机转子密实度以减少轴向力,尽量使高获能区域扭角、弦长值接近其理想值,以保证水轮机转矩满足获能效果。
2.1 修正扭角分布
由图4可知,理想扭角分布前段区域变化率比较大,增大了叶片的加工难度,前段10%R~20%R区域为轮毂与叶片连接过渡区域,设定其值与20%R处扭角值一致,对20%R~100%R扭角变化率较大区域,减小其变化率,采用高斯函数修正得到平滑曲线[14]。修正函数为:
(17)
式中:a1、b1、c1为常数,其值与λ0有关。
由图2可知,设计时,扭角的减小,会使得叶素上的入流角减小,影响获能效果,解决方法是在叶片的安装过程中,选择一定桨距角安装,弥补扭角的减小,使叶片上叶素有合适的入流角。以尖速比λ0=5、上述翼型与其在同等工况下最佳攻角为例,此时a1、b1、c1分别为0.329 1、0.633 1、0.425 7,修正后的扭角分布模型见图6。
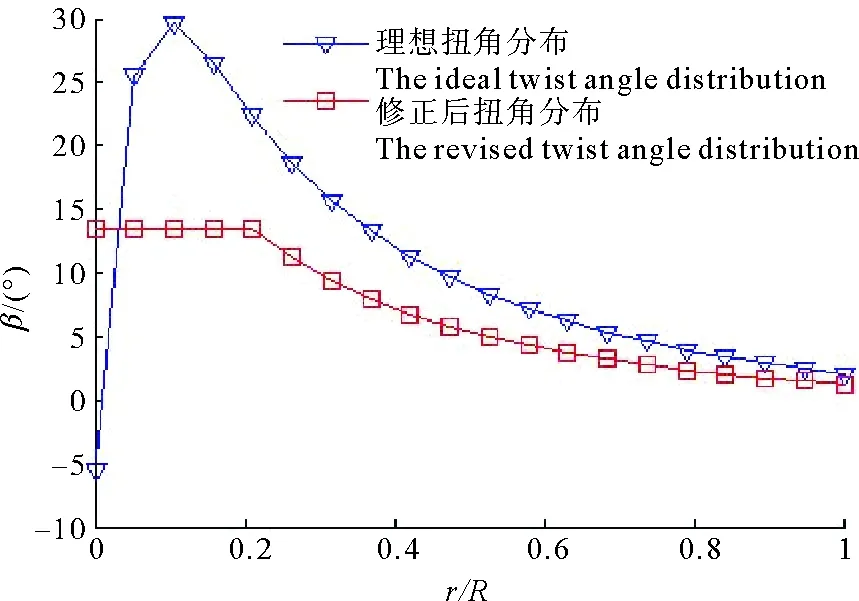
图6 修正后扭角分布Fig.6 The revised twist angle distribution
修正后的扭角分布模型在减小近段扭角变化率的同时,使远端扭角值尽量靠近其理想值附近,使得减小叶片加工难度的同时,保证叶片有良好的获能效果。
2.2 修正弦长分布
水流流过水轮机产生切向力的同时,也会产生轴向力,由切向力产生的转矩影响着水轮机的功率,而轴向力会影响水轮机稳定性及叶片寿命。仅考虑叶片上叶素弦长因素,由(13)、(14)式知,弦长增大,叶片作用面积增大,转矩、轴向力都会相应增大,若不影响水轮机转矩的同时,使水轮机有较小的轴向力,可通过减小叶片低获能区的弦长寻求解决方案。10%R以内区域为水轮机轮毂,10%R~20%R为轮毂与叶片连接过渡区域。减小20%R~100%R弦长变化率,采用高斯函数修正得到平滑曲线,修正函数为:
(18)
式中:a2、b2、c2为常数,其值与λ0有关。
以λ0=5、上述翼型最佳攻角为例,此时a2、b2、c2分别为0.441 4、1.086、1.571,修正后弦长分布见图7。
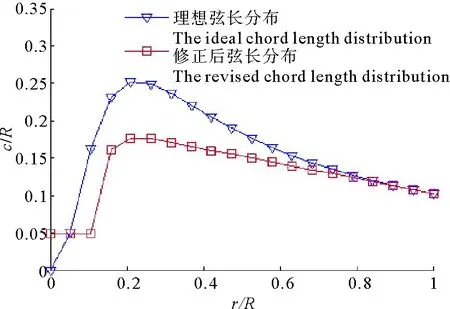
图7 修正后弦长分布Fig.7 The revised chord length distribution
修正后的弦长分布,减少近段叶素弦长值,并使整个弦长平滑过渡,以降低叶片的加工难度。修正后远段叶素值大小基本和理想值一致,以保证叶片的获能效果。
2.3 修正模型应用
将修正扭角、弦长分布模型算法应用于自主开发的潮流能水平轴水轮机设计软件叶片截面设计模块,使水轮机设计更加方便高效。叶片截面设计模块可以选择显示扭角、弦长分布数据曲线,以此数据生成叶片截面三维坐标数据。软件叶片截面设计模块界面见图8。
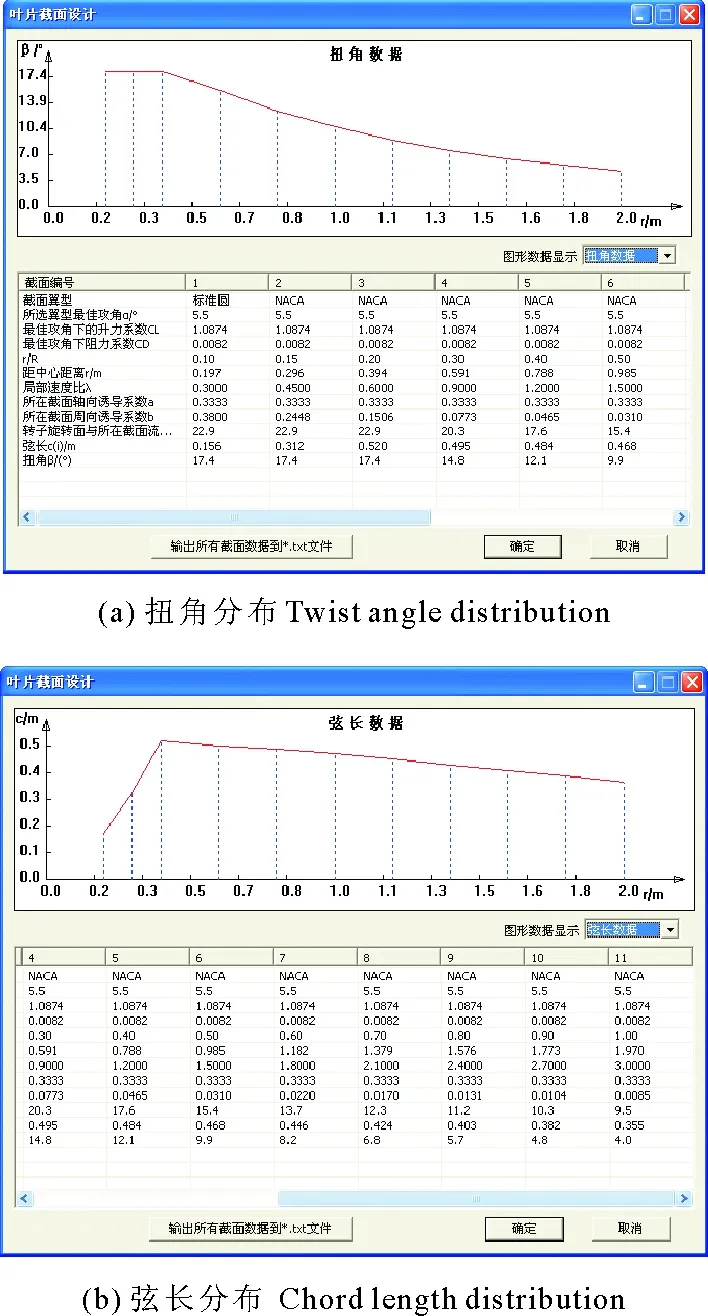
图8 软件界面Fig.8 Software interface
3 设计20 kW实例及性能分析
以国家海洋可再生能源专项资金项目“轴流式潮流能发电装置研究与试验”中的水轮机为设计实例。设计额定功率20 kW,额定流速2.0 m/s下的水轮机。选用NACA4415翼型,整体设计参数见表1。其中Cp为获能系数。

表1 整体参数Table 1 The overall parameters
采用理想模型与修正模型分别设计叶片,叶片截面数据见表2。其中cB(i)、βB(i)为理想模型弦长、扭角数据,c(i)、β(i)为修正模型弦长、扭角数据。
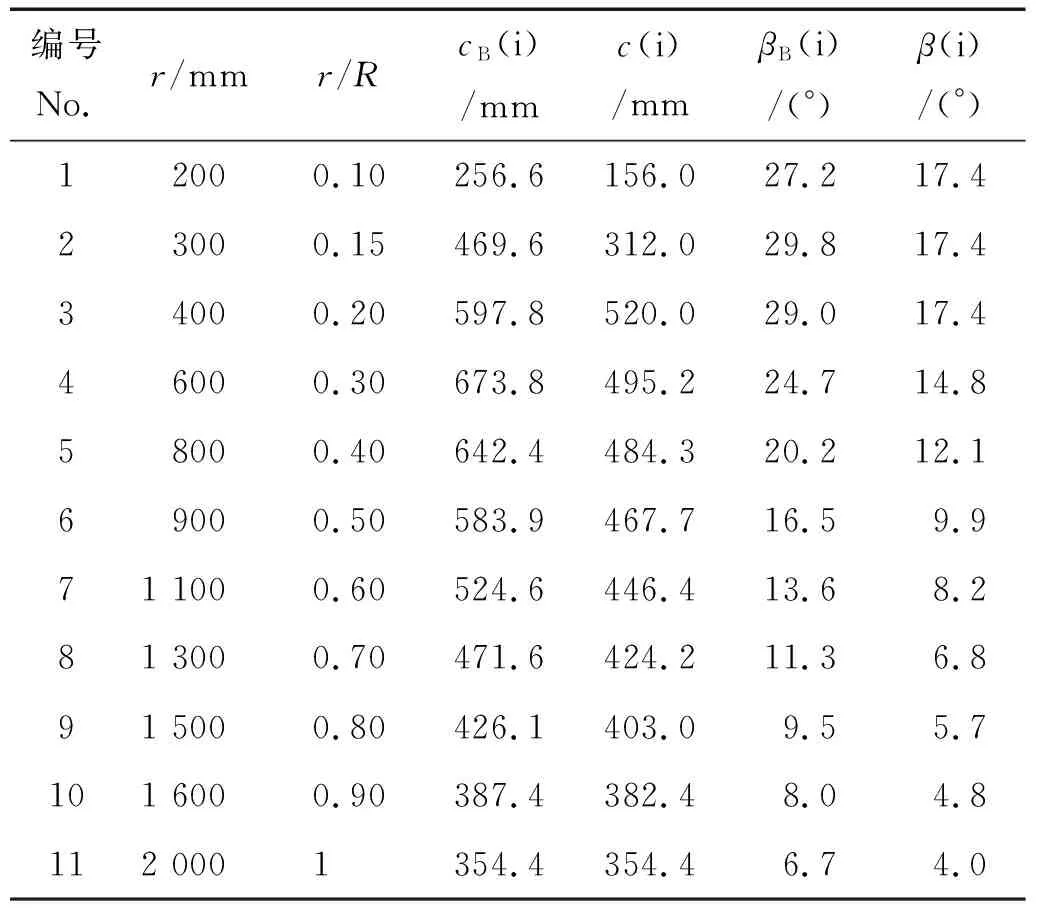
表2 叶片截面数据Table 2 The data of blade sections
采用CAD-Gambit-CFD的过程对水轮机设计分析[13],先在Solidworks中分别建立模型,桨距角0°安装叶片建立理想模型与桨距角5°安装建立修正模型,见图9。
模型在Gambit中划分网格,流体域长度设为10D(D为水轮机直径),半径选择2.5D的圆柱;旋转域仅包络水轮机,并置于距离流体域来流入口4D位置。修正模型划分网格见图10。
网格模型导入Fluent中,设置入口流速2.0 m/s、流体域转速3.05 rad/s。修正模型水轮机表面压力云图见图11。
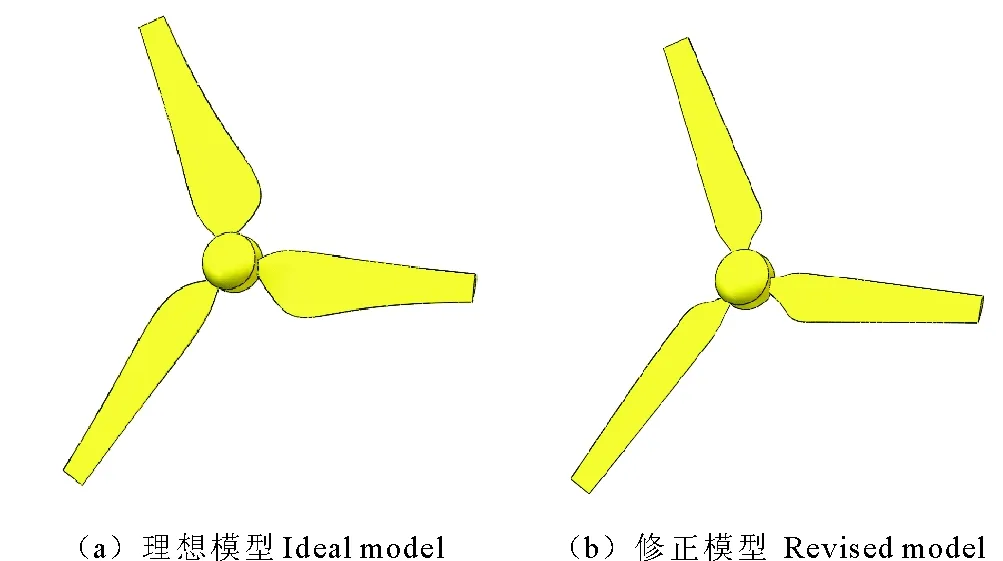
图9 水轮机转子Fig.9 Turbine motor
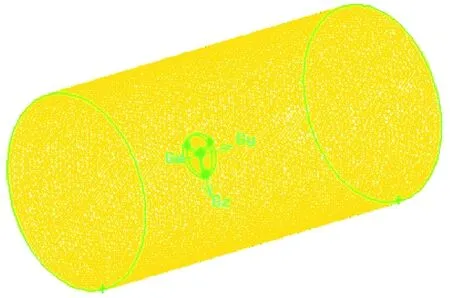
图10 网格划分Fig.10 Meshing

图11 水轮机表面压力云图Fig.11 The turbine surface stress contour
水轮机的功率由水轮机转矩与转速决定,即:
P=MW。
(19)
式中:P为功率;M为转矩。
对理想模型与修正模型性能仿真,并根据(19)式计算相应功率,结果见表3。
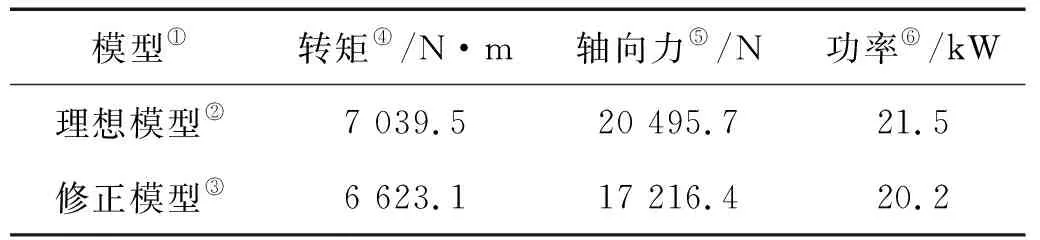
表3 性能分析结果Table 3 The results of the performance analysis
Note:①Model;②Ideal Model;③Revised Model;④Torque; ⑤Axis Force;⑥Power
数据分析得出,修正模型相比理想模型转矩减小了6%,而轴向力减少了14%,相比转矩的减少,轴向力减小较明显;并且修正模型功率为20.2 kW,说明其转矩满足获能功率要求。水轮机表面的压力云图显示也验证了水轮机叶片高获能区在远段区域。
实际模型制造中还需考虑叶片表面粗糙度、内部加强筋结构、叶片根部弯矩等,通常叶片近段采用相对厚度较大的翼型,并在内部、根部做加固处理,使叶片满足强度要求[15-16]。根据上述,制造叶片见图12,并安装到水轮机,载体与支撑结构采用坐底式浮箱结构,整体装置在斋堂岛海域进行海试,启动流速在0.8 m/s,流速2 m/s及以上时发电功率满足要求,流速大于2 m/s时,改变叶片桨距角,使发电量保持在20 kW,流速与发电量的关系见图13。海试过程中,整体装置满足抗滑移、抗倾覆要求。水轮机整体发电装置见图14。

图12 叶片Fig.12 Blade
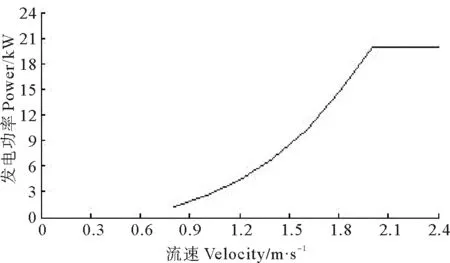
图13 Power curveFig.13 发电功率曲线

图14 水轮机发电装置Fig.14 Turbine power generation device
4 结论
本文采用解析计算与CFD仿真结合的方法对水轮机设计中叶片扭角、弦长分布进行研究。解析计算方法推导叶片扭角与弦长的理想分布模型,并考虑水轮机安全平稳运行的要求,对理想模型进行修正得到修正模型,并对理性模型与修正模型仿真,对其性能情况进行对比。得出结论如下:
(1)叶片扭角理想分布是关于尖速比λ0、转子半径R、距旋转中心距离r、最佳攻角αB的函数。设计时,尖速比取值越大,扭角值越小。
(2)叶片弦长理想分布是关于尖速比λ0、转子半径R、距旋转中心距离r、叶片数B、最佳攻角下的升力系数CL、阻力系数CD的函数。设计时,尖速比取值越大,弦长值越小。
(3)理想模型与修正模型性能分析得出,修正模型转矩满足获能功率要求,轴向力明显减小。仿真验证叶片的高获能区在远段区域,对理论计算的叶片扭角、弦长修正有利于提高水轮机的综合性能。
本文研究还不能量化分析修正模型转矩、轴向力减小的权重关系,文中采用简化海况流场模型对水轮机理论分析与数值模拟,指导水轮机叶片设计。实际海况复杂多变,还需要更深入研究复杂流场下水轮机水动力学性能并结合工程实践,进一步提高发电装置的可靠性、稳定性、安全性。另外,叶片选用翼型的水动力学特性对水轮机性能有很大影响,适用于潮流能水轮机叶片的专用翼型还有待进一步的研究。

