课堂生成，课堂生命的“活水”

（云南师范大学附属世纪金源学校 云南昆明 650000）

本文从《最短路径问题》（本人执教）和《圆锥的侧面积》（校外听课）两节的具体教学谈谈我对课堂生成这一资源的把握和使用两方面谈谈我的看法。

一、《最短路径问题》的教学

本节课是为参加我校2015-2016学年青年教师课赛而准备的，正式比赛之前，我经历了四次磨课，在课题的引入方式、学生的小组讨论题目、例题的设计方面都进行了修改，也得到了同组多为老教师的指点，借此机会也想他们表示感谢。

本节课分以下四个步骤进行教学：

1.知识准备

完成以下题目，回顾垂直平分线的性质和作已知点关于某直线的对称点两个知识：

（1）如图，在△ABC中，EF是AC的垂直平分线，AF=12，BF=3，则BC=_______。

第1题

第2题

（2）如图，已知对称轴EF和一个点A，画出点A关于EF的对称点A′

结果：学生反应很快，看到题目1马上联想到线段垂直平分线上的点到线段两个端点距离相等，并很快得出了答案15.

2.提出问题

问题1：如图，某煤气公司要在输气管道L上修建一个泵站，向小镇A供气，泵站建在什么位置能使输气管线最短？

结果：学生看到问题1后很快想到了垂线段最短这一重要结论，并很快想到了解决的方法，即：过点A作直线l的垂线，垂足即为建泵站的地方。

问题2：如果所建泵站还要向B镇供气，泵站又该建在什么位置才能使输气管线最短？

教学细节：将问题抛给学生后由学生进行小组讨论，并给出解决问题的方法，学生发现要解决问题2，必须分以下两个步骤：

第一，确定小镇B的位置，可有以下三种：

从安全的角度考虑，小镇B不可能在B2的位置，即：建泵站时只需考虑小镇A、B在输气管道l的同一侧和两侧两种情况。

第二，分以下两种情况讨论建泵站的位置：

情况一：小镇A、B在输气管道l的两侧

如图，泵站建在点P处，可使输气管线最短

结果：看到上图（左）后，几乎所有学生都想到了两点之间线段最短，并快速给出上图（右）的答案。

情况二：小镇A、B在输气管线l的同侧

教学细节1：学生对情况二展开了热烈的讨论，由学生板演给出以下两种答案：

答案1

答案2

教学细节2：教师通过几何画板的动画演示，直观感知泵站的选址

教学细节3：观察动画，初步断定答案2正确，经过讨论发现答案1中的P点是到A、B两镇距离相等的点，并不是线路最短的点

教学细节4：引导学生对答案2进行论证，得出结论。

结果：以学生自己发现问题（先确定小镇B的位置）→讨论出解决问题的方法（包括错误答案）→观看动画演示，否定自己给出的错误答案→归纳方法的方式展开教学，层层递进，有助于学生更好的理解最短路径问题的解决方法，并很好的调动了学生学习积极性，几乎所有的学生都参与了课堂学习活动，教学效果较好。同时，在讨论过程中学生提出的不同答案也给本节课注入了活力，成为精彩亮点。

二、《圆锥的侧面积》的教学

本节课是我在回母校看望初中班主任时，请他给我安排听的一节课，是新人教版九年级上册中的一节新授课，下面就其中的几个教学片段谈谈我的看法。

因为圆锥的侧面展开图为扇形，所以扇形的面积即为圆锥的侧面积，而无论是计算弧长还是扇形面积都需要圆心角这一元素，因此要解决圆锥侧面积的问题就要先算出圆锥的圆心角。

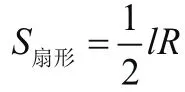
图1

教学片段二：例题之后的变式训练的处理

练习1：如图，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为（ ）

A.288° B.144° C.216° D.120°

学生：可以先求其侧面展开图扇形所在圆的周长，再……

老师狠心的打断了学生，没有让他继续说下去，而是按照自己的预设要求学生用方程思想来解决此题。

我的看法：固然此题用方程的思想解决能很快得出答案，但是学生在没有经历复杂的计算之前，就只能听老师讲这是最简洁的方法，而不是理解。我相信这位老师在备课上是做足了功夫的，每一个例题和变式训练题都是经过精心挑选的，力求做到精讲多练，让学生快速掌握解题的技巧，但他忽略了一点，教学不仅要让学生知道结果，还要让学生理解为什么要这样，我们的教学效率才能真正的提高，才能培养学生的创新精神和实践能力。

思考

教是为学服务的，学生才是课堂的主体，而课堂内学生的基础是存在差异的，学历能力也不同，真实的课堂与教师的预设并不吻合，甚至会有很大的差距，这就要求教师不断调整教学思路，借助课堂内出现的问题，把握好真实的课堂。每节课都要尽量做到利用生活实例引入课题，激起了学生的探索兴趣，又让学生自由讨论，自己发现问题、提出问题、推出矛盾，最终解决问题。在问题的提出过程中允许学生的错误存在，也让错误成为下一步的讨论点之一，让学生自己否定了错误答案，教师再辅以适当的点拨，这样做既丰富了知识，又拓展了思路，训练了学生的思维灵活性和创造性，这样的教学更精彩，更真实。

随机的课堂是教师、学生、知识之间信息的传递场所，学生不仅是学习的主体，更是课堂生命的“活水”，课堂上随机产生的新思想、新问题（无论对错），新的表达方式都会使我们的课堂活起来，把握好每一个精彩的瞬间生成，我们的课堂效率必将得到大大的提高，必定能在有限的四十分钟内创造出更多的精彩。