算法分析与设计的研讨型教学模式探讨

张小峰 宋丽华 雷 鹏

鲁东大学信息与电气工程学院 山东烟台 264025

“程序=数据结构+算法”，计算机大师尼古拉斯•沃斯用非常简洁的公式指明了算法在程序设计中的重要性。然而，与一般的课程不同，算法对学生的数学基础、逻辑思维能力要求较高，强调对知识的理解和应用，要求理论与实践结合，知识与能力并重。由于算法课程具有上述特点，传统的授课方式不适用算法的教学，如果授课教师不注意教学方法、教学模式等方面的研究，学生可能在算法的学习上不会有太多的收获。为了有效解决学生在学习算法时的困难，从一定程度提高学生的算法设计能力，许多高校对于算法课程的教学采用了不同的方式。例如，将算法和数据结构课程合并，开设数据结构与算法，对一些非常经典的算法和问题进行分析；甚至有的高校直接将算法设计与分析安排为选修课，仅供有能力的学生选修。笔者认为，算法是计算机类专业中的核心和主干课程，这在CC2001三种不同层次的教程模型中也有所体现。因而，采取不回避、不逃避的态度，积极围绕算法分析与设计的教学内容，认真设计教学案例，改进教学模式和教学方法，切实提高教学效果，这也是计算机教育界在进行算法授课时共同面对的问题。

1 算法分析与设计授课中存在的问题

算法分析与设计课程是计算机、软件工程等专业的核心和主干课程，除了要求学生掌握离散数学、数据结构等先导课程的基础知识外，还要求学生具有较强的逻辑基础和抽象思维能力。然而，目前的算法分析与设计的教学过程中存在许多问题，主要有以下几点。

(1)学生对课程在教学体系中的重要性认识不够。算法是计算机课程体系中的核心课程之一，通常被安排在离散数学、数据结构等先修课程后开设。然而，许多学生认为，计算机类专业的学生应该掌握相关的前沿技术，不需要过多地对思维进行训练，为算法分析与设计的学习埋下了隐患。

(2)学生不具备必要的学习素质。在普通高校应用型人才培养的课程体系中，大量的课程被压缩课时，导致许多课程内容被压缩、删减，导致应扩展的知识点没有得到扩展，产生的直接后果就是学生的基础不扎实。特别是离散数学、数据结构等算法的先修课程的基础不扎实。

(3)许多学生学习缺乏必要的兴趣与动力。对于逻辑性强、难度大的算法课程而言，许多学生没有意识到算法的重要性，特别是在一般的高校中，在他们的观点中，算法不像技术类课程那样，可以带来最直接的收益。

(4)教师的教学模式和教学方法亟须改进。算法的逻辑性与难度同样给授课教师带来了许多困难，许多教师对于算法的授课，通常有两种模式：一种是讲解算法的思想，让学生编程实现；另一种是降低课程的难度，从程序设计的角度实现相关的算法。从专业的角度看，这两种教学模式适用于不同的高校，第一种适合培养高水平高校的学生，第二种则对非计算机类专业的学生适用。

2 算法分析与设计中实施研讨型教学的探索

算法分析与设计是一门面向能力与思维培养的专业核心课程。与一般的计算机类专业核心课程相比，算法的核心内容相对比较少，主要集中在递归与分治、动态规划、回溯、分枝限界和贪心算法等几种主要算法上，但由基础算法扩展的相关问题却较多，不同的教师可以根据学生的不同情况选择相应的问题。

“授之以鱼，不如授之以渔”，掌握相关的问题，不如掌握求解问题的思想。从这个角度看，算法分析与设计课程非常适合引入研讨性教学。这种教学模式对教师而言，要求设计的问题具有启发性，由易到难，由简到繁，采取循序渐进的教学。对学生而言，要求学生真正成为学习行为的主人，在学习过程中发掘自身的潜力，施展才华，在课堂教学中处于教学主体地位。在算法分析与设计中采取研讨型教学，可以为学生提供思考问题和讨论问题的机会，使学生围绕相关的算法，应用所学的知识解决相关的问题。这种教学模式，能使学生增长知识、开阔视野，有助于学生综合能力的提高，还有助于师生共同探索、发现和研究，进而密切师生关系，促进教学相长。

2.1 算法课程由选修提升到必修 增加算法的课时

在修订培养方案时，笔者所在的高校充分认识到算法课程在学生能力培养中的重要性，将算法分析与设计从选修课修订为必修课，这样可以避免许多学生在选课时回避这门课程，从一定程度上提高学生对算法课程的重视程度。同时，将算法的课时设置为54课时左右，保证了教师有充足的时间讲解课程的内容。

2.2 有针对性地选择授课内容 避免盲目性

一般地，算法主要包括[1]：枚举法(暴力搜索)、递归法、分治法、动态规划、贪心算法、回溯法、分枝限界法、随机化算法、线性规划与网络流等相关算法，授课内容也是根据学生的具体情况，围绕几种典型算法介绍相关的问题，强化对相关算法的灵活应用能力。在授课内容的设计中，根据课时的需要，删减了随机化算法以及线性规划与网络流两种经典算法，重点围绕其他7种算法讲解，每一种算法设计3～5个典型问题重点讲解，同时安排学生讲解3～5个问题，进一步熟悉相关算法。对每一个问题，从问题分析、算法的设计思想、解决问题的思路以及编程过程要求详细地讲解，不放过任何一个细节，切实提高算法设计能力和编程水平。表1列举了笔者在授课过程中教师讲授和学生练习的相关经典题目。

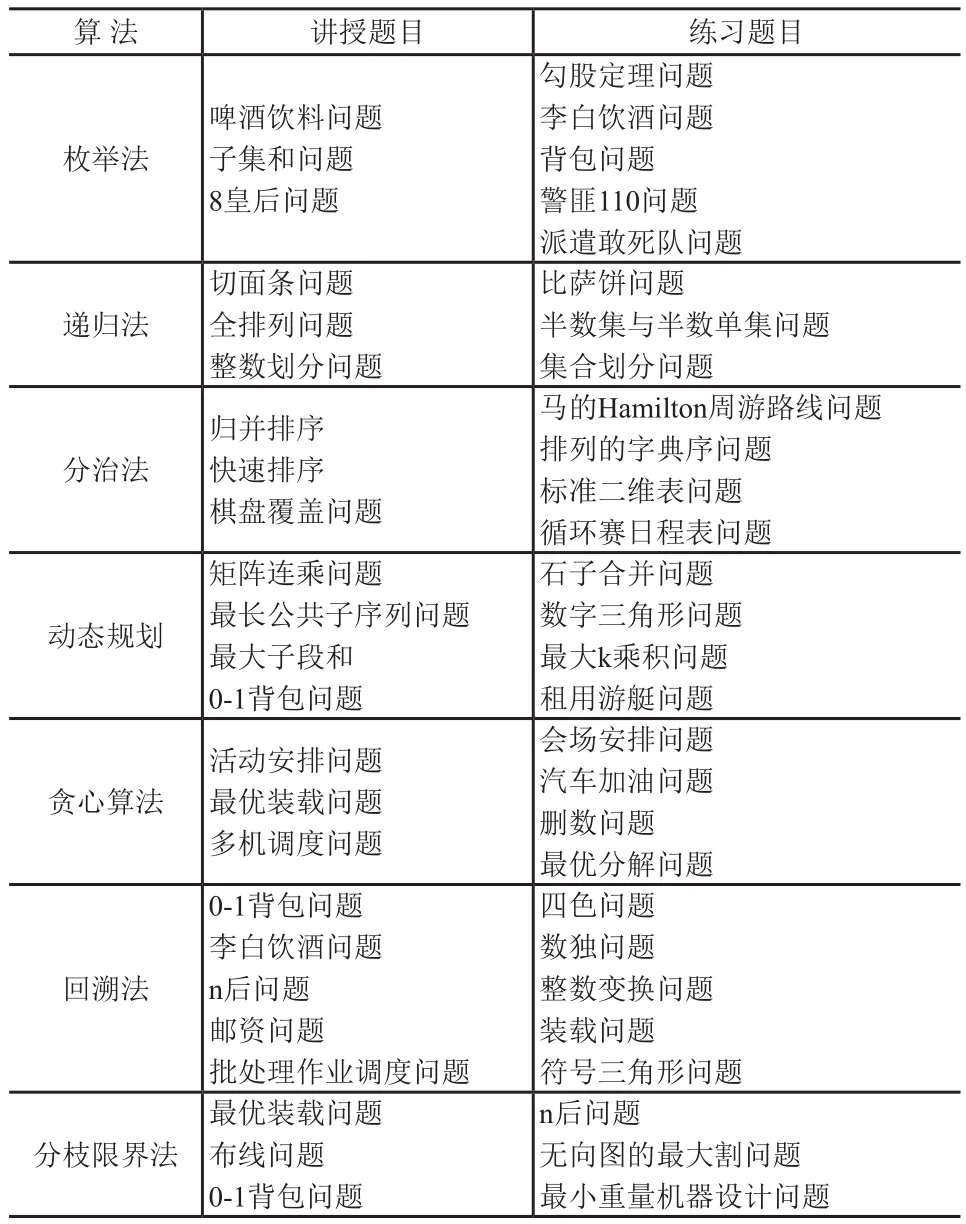
表1 授课过程中授课和练习的主要问题

2.3 注意知识讲解的递进性

由于算法课程的难度，在讲解算法时，需要按照由易到难的原则，让学生逐渐掌握算法的精髓。这里以回溯法为例进行介绍。回溯法的精髓在于设计解空间的树结构是通过对解空间树进行深度优先遍历完成的。按照问题解空间的组织形式，解空间树有子集树和排列树两种形式。一般而言，排列树比子集树更复杂，在讲解过程中，可以把排列树安排在子集树后讲解。而在构造子集树时，需要重点考虑参数的个数和子集树的高度两个主要因素，在构造回溯函数时，则需要重点考虑参数的个数和参数的含义。在设计时应按照知识的递进性，由易到难构造不同的子集树。笔者在授课过程中设计了4个教学案例：0-1背包问题、李白饮酒问题、8皇后问题和邮资问题，分别对上述问题进行了解释和说明。

2.4 教学过程中需要重视案例的设计

算法课程在授课时，需要注意相关案例的设计。一般来讲，案例的设计应具有代表性、实用性，从案例设计的角度培养学生的学习兴趣。例如，在介绍回溯法时，可以通过8皇后、数独这些生活中的实际问题对回溯法进行分析，提高学生的学习兴趣。

同时，备课时要注重案例的设计应遵循“由易到难，由简到繁”的原则，逐渐培养学生的算法设计能力[2]。以枚举法为例对案例的设计进行说明，在介绍枚举法的基本思想后，通过“啤酒饮料问题—子集和问题—8皇后问题”三个问题介绍枚举法的基本思想以及实现枚举法中的细节处理。

2.5 注重算法设计中的数学思想

算法的设计离不开数学基础，好的数学思想会让算法的设计事半功倍，教师在授课过程中不能仅仅满足算法的实现，而更应该通过相应的数学思想，对学生的思维和算法设计能力进行训练[3]。通过最大间隙问题、最多约数问题、整数划分问题3个例子说明。

在最大间隙问题中，如果不考虑算法的复杂度，可以直接对给定的数进行排序，线性扫描一次后可以得到最大差值。然而，排序算法的最优时间复杂度明显不满足线性时间的要求，因此，需要借助离散数学中的鸽笼原理这一关键数学思想设计相应的算法。在最多约数问题中，如果没有算法基础，可以通过简单的循环也可以计算出来，但更优秀的算法可以结合算术基本定理实现。在整数划分问题中，虽然可以通过递归得到整数划分的递推公式，但如果教师在授课过程中将整数的划分问题变成多项式的乘法，引入母函数法，从另一个角度讲解正整数的划分，不仅可以加深学生对划分问题的理解，也可以进一步开阔学生的视野。

2.6 注重对问题的纵向和横向扩展

在算法分析与设计的授课中，对给定的问题，不能仅局限一种算法，也不能仅局限在这一个问题上，要注重对问题的纵向和横向扩展。例如，介绍棋盘覆盖问题时，通过判断特殊格的位置，可以将问题分解为4个子问题，在不包含特殊格的3个子问题交接处，构造1个特殊的L型骨牌，这样问题就可以运用分治法求解。按照这个思路，可以对马的Hamilton周游世界问题进行同样的分析，将1个问题分解为4个子问题，运用同样的思路求解，以加深学生对分治法的理解。例如，在求解0-1背包问题时，可以运用枚举法、动态规划法、回溯法、分枝限界法对问题进行求解，让学生比较几种算法的优劣，以加深对相关算法的理解。同样，在介绍动态规划算法时，可以对每一个问题用递归算法、备忘录算法和动态规划算法实现，让学生彻底理解自下向上和自上向下两种不同的设计思想。

2.7 注重宏观与微观上算法的教学

讲授算法时，笔者认为授课教师应该注重从宏观和微观两方面把握算法的教学，即不仅讲授算法的思想，而且应该讲授算法的具体实现。如果仅仅停留在算法思想的层次，能力较差的学生会失去兴趣而直接放弃算法的实现。同时，注重微观上的教学，除了可以让学生深入了解算法的思想外，还可以进一步熟悉和掌握先修课程的相关知识。以8皇后问题为例进行说明。

在8皇后问题中，如果用枚举法实现，可以简单为每一个棋盘格设计一个变量，判断在该棋盘格是否放置皇后。这样进行简单的枚举，需要考虑的可能数量为264。类似汉诺塔问题，该问题在理论上可以求解，但实际情况无法求解，无法在有效时间内解决。在算法实现时，可以借助数据结构对问题进行简化。通过引入一维数组，保证每一列上只有一个皇后，可以将变量数从64减少到8，将需要考虑的情况减为28=256，进一步运用枚举法，可以得到8皇后问题的解。

通过这样的教学，不仅可以让学生进一步理解和掌握枚举法的思想，而且可以熟悉和掌握数据结构在算法设计中的作用，提高学生的学习兴趣。

3 结语

在算法分析与设计中实施研讨型教学，笔者已经探索了3年。这种教学模式受到了学生的普遍欢迎，除了编程水平、算法设计能力得到了较大的提升外，思维能力以及分析和解决问题的能力也得到了一定的训练。有多名学生参加全国程序设计大赛获奖，有多名学生考取了西安电子科技大学、天津大学的研究生，并且在复试阶段得到了较高的评价。同时，实施研讨性教学，对于密切师生关系，提高教师的教学水平，充实教师的教学内容也大有益处。实践证明，在算法分析与设计课程的教学中实施研讨型教学，对计算机类专业培养高水平的应用型人才大有益处。