Al-Ti-B合金中AlB2、TiB2和TiAl3的第一性原理研究

黄元春，邵虹榜，肖政兵，任贤魏，郭晓芳



Al-Ti-B合金中AlB2、TiB2和TiAl3的第一性原理研究

黄元春1, 2, 3，邵虹榜1，肖政兵1, 2, 3，任贤魏1，郭晓芳1

(1. 中南大学 轻合金研究院, 长沙 410083；2. 中南大学 高性能复杂制造国家重点实验室, 长沙 410083；3. 中南大学 机电工程学院, 长沙 410083)

采用基于密度泛函理论的第一性原理方法，研究0 K条件下Al-Ti-B体系中AlB2、TiB2和TiAl3的平衡晶格常数、形成热、结合能及电子特性，并结合准简谐德拜模型对3种物相在高温条件下的热力学基本性质进行了分析。计算结果表明：AlB2、TiB2和TiAl3的形成热与结合能均为负值，表明3种相均具有结构稳定性，且稳定性由大到小依次为TiB2、TiAl3、AlB2；3种物相的离子性与金属性由大到小依次为TiAl3、AlB2、TiB2，TiAl3与AlB2显示离子键特性，而TiB2键合特性以共价键为主；3种物相的热稳定性由大到小依次为TiB2、AlB2、TiAl3。计算所得TiB2、AlB2和TiAl3的热力学性质可以用于分析氟盐法制备Al-Ti-B时Al熔体与氟盐之间反应发生情况以及中间合金最终的物相组成。

Al-Ti-B合金；第一性原理；准简谐德拜模型；结构特性；热力学性质

商业用Al-Ti-B的常用制备工艺是将高纯铝锭熔化，通过加入不同比例的混合氟盐(K2TiF6、KBF4)至铝熔体中并保温反应一段时间后浇铸，从而得到不同Ti/B比例的Al-Ti-B中间合金[1−2]。Al-Ti-B中的第二相粒子(如TiB2、TiAl3和(Al,Ti)B2等)有助于铝发生异质形核而达到细化晶粒的效果。例如，Al-5Ti-1B加入至Al熔体后释放出的高熔点TiB2粒子可以作为(Al)异质形核的核心，低熔点的TiAl3在铝熔体中能被迅速溶解并释放出Ti元素，为(Al)发生异质形核创造了便利条件[3−4]；而KORI等[5]研究发现Al-1Ti-3B中AlB2含量较高，适于Al-Si合金的晶粒细化。尽管Al-Ti-B中间合金具有细化效率高、成本低廉等优点而广受青睐，然而在实际应用过程中仍存在如内部第二相粒子聚集沉淀、尺寸宽化等诸多缺陷[6−7]，严重限制Al-Ti-B在高质量铝材生产中的应用。因此，深入了解这些异质形核粒子的结构与性质就显得尤为重要。

到目前为止，不少研究者[8−10]试图解释制备过程中氟盐在铝熔体中的反应机制及情况，以改良Al-Ti-B的制备工艺，从而进一步开发Al-Ti-B的细化潜能。然而，K2TiF6、KBF4与Al的反应生成TiB2、TiAl3等中间相的过程受化学反应机制、元素扩散等众多因素影响，难以精确分析熔体中氟盐反应机理。本文作者采用基于密度泛函理论(Density functional theory，DFT)[11−12]的第一性原理方法，研究AlB2、TiB2和TiAl3的结构稳定性以及电子特性，并结合准简谐德拜模型对这3种物相在高温条件下的热力学基本性质进行分析，期望从原子角度揭示3种物相在Al-Ti-B体系下的基本性质，为开发新型高品质Al-Ti-B制备工艺提供理论支撑。

1 计算方法与模型

在结构稳定性与电子结构的研究方面，本文作者采用基于密度泛函理论的第一性原理平面波赝势方法，并在计算过程中使用广义梯度近似 (Generalized gradient approximation, GGA)[13]处理交换关联能，交换关联势采取Perdew-Burke-Ernzerhof (PBE)[14]形式 进行。各元素价电子的选取情况如下：B-2s22p1、Al-3s23p1、Ti-3s23p63d24s2。AlB2、TiB2和TiAl3晶胞模型简约布里渊区K-point采取Monkhorst-Pack[15]方法划分，单胞网格数分别取10×10×8、10×10×8和8×8×8。自洽循环计算的能量收敛精度设置为1×10−6eV/atom，各个原子之间的相互作用力低于0.01 eV/nm，公差偏移低于5.0×10−4nm，应力偏差为低于0.05 GPa。

采用准简谐德拜模型[16]对TiB2、AlB2以及TiAl3的等容摩尔热容、熵值以及热平衡体积与热膨胀系数随温度的变化进行了研究。3种物相的非平衡Gibbs函数*(;,)为可描述为

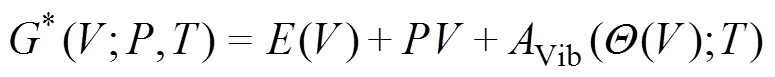
式中：()表示3种物相每个原胞体积下的总能量；、和分别为压强、体积和温度；()为德拜温度；Vib为振动Helmholtz自由能。

而基于准谐近似和使用声子态密度的德拜模型，Vib可以用以下形式表示[17]：

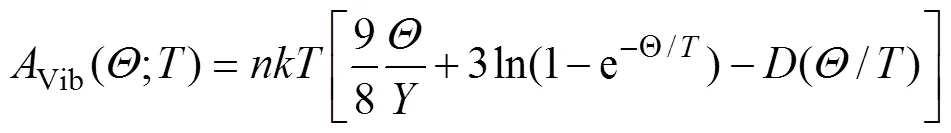
式中：代表每个原胞中所含原子数目；为波尔兹曼常数；(/)为德拜积分。

各向同性固体的德拜温度表示如下[16]：

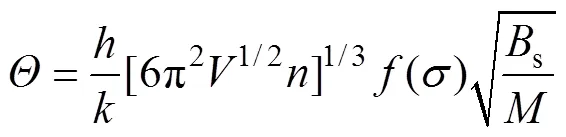
式中：为每个原胞中分子的质量；s是表征晶体压缩率的绝热体弹模量，可以近似写为

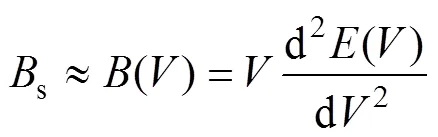
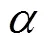
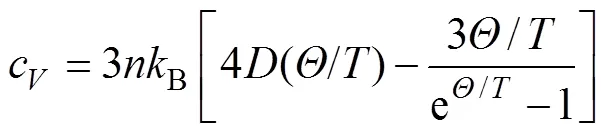
2 结果与讨论

2.1 晶体结构与稳定性

TiB2(AlB2)属于六方晶系，空间点群为6/，每个晶胞含有1个Ti(Al)原子和2个B原子，Ti(Al)原子占据六棱柱的顶角和底心位置，而硼原子处于中心；TiAl3具有四方晶体结构，属于4/空间点群，晶胞由两个面心立方晶格堆垛构成，包含2个Ti原子和6个Al原子。通过充分驰豫晶胞结构以及晶内原子位置以达到能量最低状态，对3种物相的结构稳定性进行研究分析。

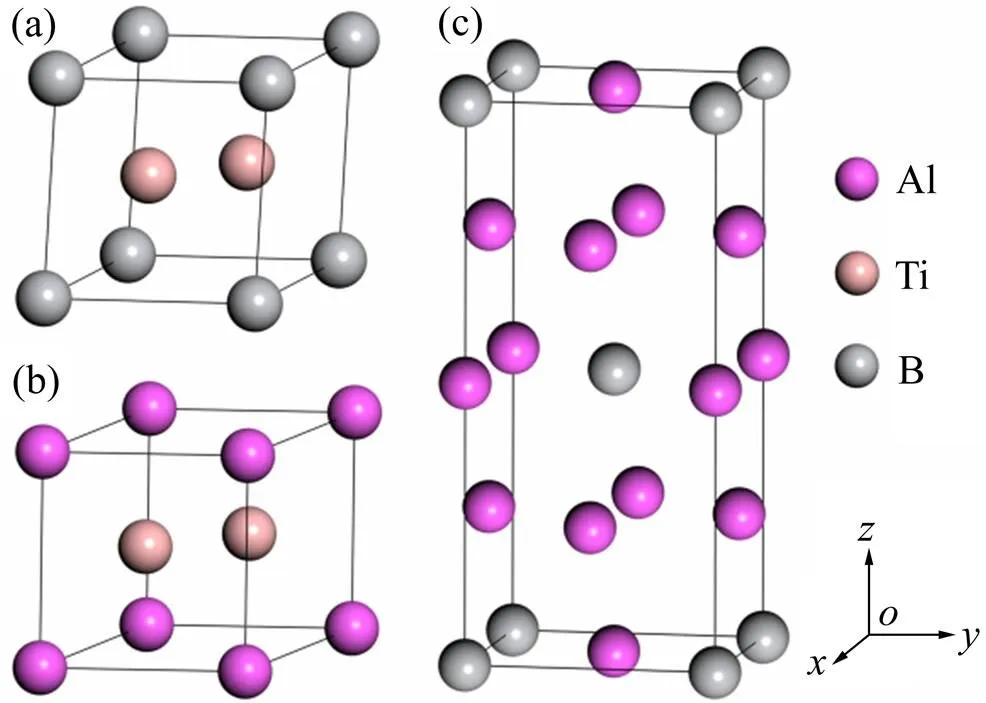
图1 TiB2、AlB2和TiAl3的晶体结构模型

晶体形成热(Heat of formation, Δ)用以表征物质由单质状态转变成晶体化合物状态的反应过程中能量的变化情况：Δ为负值时，表示化合物在形成过程中放热，反应可自发进行；反之则为吸热，反应需要外界提供能量才能进行，且生成的化合物不稳定。结合能(Cohesive energy,coh)是指原子由自由态结合成为晶体化合物的过程中所释放的能量，用来表征化合物形成之后在结构上的稳定性，结合能的绝对值越大，则形成的晶体化合物越稳定[21]。对于化合物AB，其形成热与结合能的计算公式分别如下[22]：

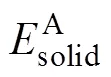
AlB2、TiB2和TiAl3的晶体结构参数以及形成热与结合能的计算结果如表1所示。通过比较可以发现，所得计算结果与实验测量值误差较小，表明本研究所采用的计算参数设置合理。

计算结果显示：TiB2、AlB2以及TiAl3的形成热均为负值，表明3种物相的形成过程无需外界提供热量，均能自发进行；从结合能的计算结果来看，3种物相的结合能绝对值由大到小的依次为TiB2、TiAl3、AlB2，说明Ti原子与B原子结合能力最强，所形成的TiB2相熔点最高。此外，比较两种硼化物可以发现TiB2的结合能低于AlB2，说明在Al-Ti-B中间合金中TiB2更加稳定，与文献[23]的研究结果相符。形成热与结合能的结果表明，3种金属间化合物的稳定性由大到小依次为TiB2、TiAl3、AlB2。

2.2 电子结构

为了解TiB2、AlB2和TiAl3的成键特性，并进一步揭示出3种物相的结构稳定性差别，本研究中分别计算了3种物相的总态密度(Total density of state, DOS)和分态密度(Partial density of state, PDOS)，结果如图2所示，图中虚线表示费米能级(Fermi level)。

表1 计算所得TiB2、AlB2以及TiAl3的晶体结构参数、形成热与结合能以及实验值

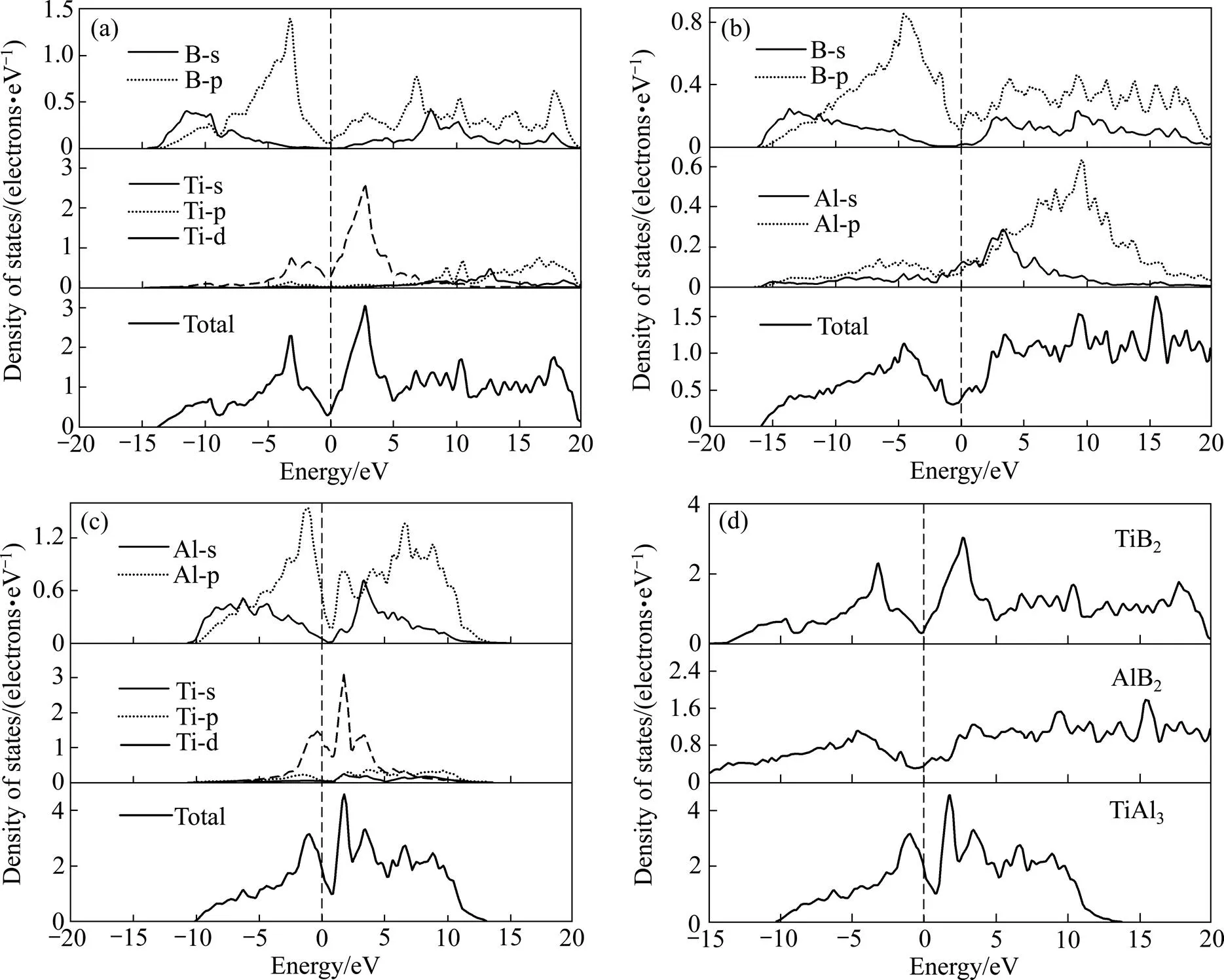
图2 物相的分态密度与总态密度

TiB2、AlB2和TiAl3在费米能级处的态密度均大于0，显示不同程度的金属特性。图2(a)显示TiB2中B 2s与2p的态密度发生重叠而产生sp态杂化。Ti原子PDOS显示3d轨道在费米能级附近呈现出两个尖峰，而与3d轨道重合的s和p轨道在费米能级附近的态密度较弱，这是由于Ti 3d、4s和4p轨道之间的杂化而造成的[28]。B 2p与Ti 3d轨道态密度尖峰分列在费米能级左右而显示出较强的杂化，并使得TiB2的总态密度在费米能级处出现赝能隙，反映了TiB2存在较强共价键特性；图2(b)显示AlB2中B 2s与2p态密度同样存在重叠现象，但与TiB2相比，重叠的能量范围更为宽泛，而且在费米能级以上(0~20 eV)空轨道中的态密度更大，这表明AlB2的反键合态更高。另一方面，Al原子在费米能级以下存在的sp态杂化较弱，而且在高能量区域的反键合态较强。因此，Al原子的价电子对AlB2的共价键几乎没有贡献。AlB2的总态密度相对平滑，而且在费米能级处存在平坦的能隙，意味着成键轨道与反键轨道之间的能量差异较小，共价键的键合强度比TiB2弱。图2(c)显示TiAl3的总态密度集中在−10~15 eV的能量范围，并且在费米能级附近存在赝能隙，表明TiAl3同样具有一定的共价键特性。然而该能隙范围较窄，说明TiAl3的共价键强度弱于两种硼化物。分析TiAl3的PDOS可知其总态密主要来自Al 3s和3p以及Ti 3d轨道价电子贡献(d轨道的PDOS为较大的尖峰，该轨道电子相对比较局域)。此外，Al 3p与Ti 3d的PDOS在费米能级附近发生重叠，存在Al 3s和Ti 3d态电子杂化。

Mulliken电荷布居分析可以定量地描述3种物相内部电荷转移情况，其结果如表2所示。

从表2中可以看出，TiB2中Ti原子转移到B原子的电荷数为1.16，转移的电荷主要来自Ti原子4s轨道；AlB2中Al原子转移到B原子的电荷数为1.29；而TiAl3中除了Al 3s和Ti 3d轨道电子杂化产生电荷转移(Ti原子转移到Al原子的电荷数为0.06)外，Al的sp轨道杂化使得单位Al原子之间产生0.10的电荷转移。以上结果表明，3种相均出现了电荷转移，原子之间除了共价键之外，还存在着离子键特性，离子性按以下顺序增加，由大到小依次为TiAl3、AlB2、TiB2。

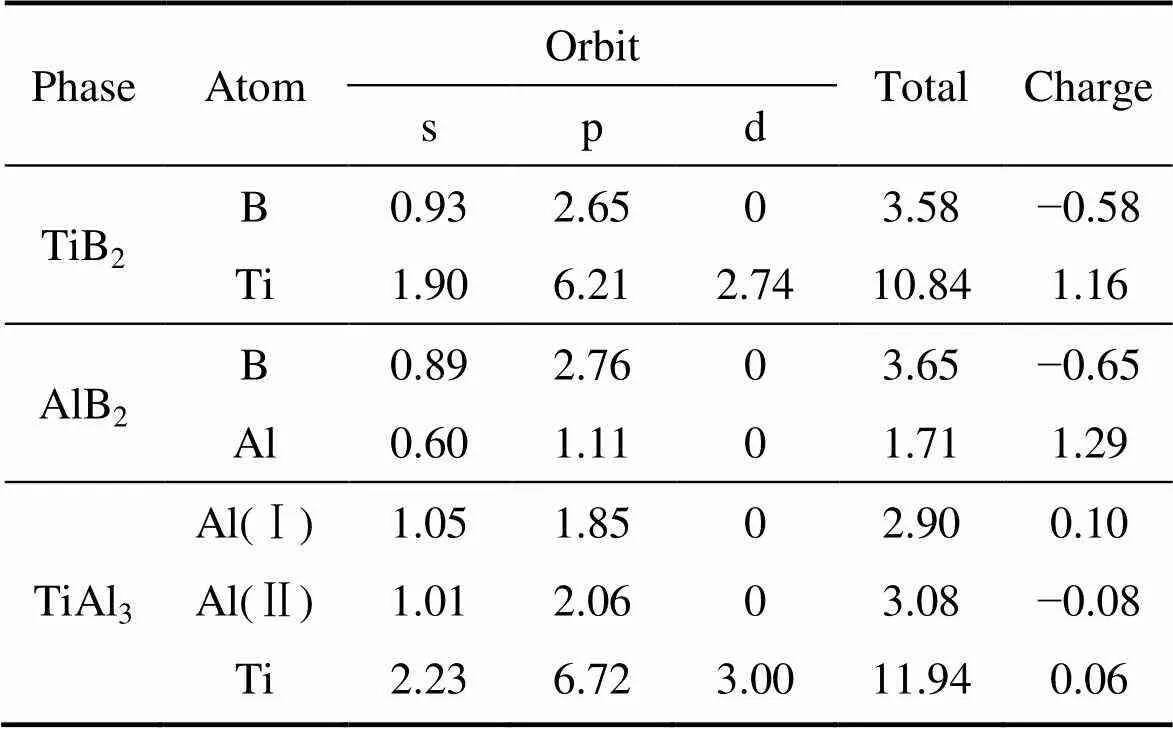
表2 TiB2、AlB2和TiAl3 的Mulliken电荷布居

TiB2、AlB2以及TiAl3的金属性(m)可以通过以下计算公式[29]得到

式中：F为费米能级处态密度值；m、e分别为晶胞内热激活电子、价电子的密度，而e可由晶胞体积(cell)与总价电子数()计算得到：e=/cell。相关参数以及计算结果如表3所示。由表3可以看到，TiAl3的m相对较大，其次是AlB2，而TiB2的金属性最小。

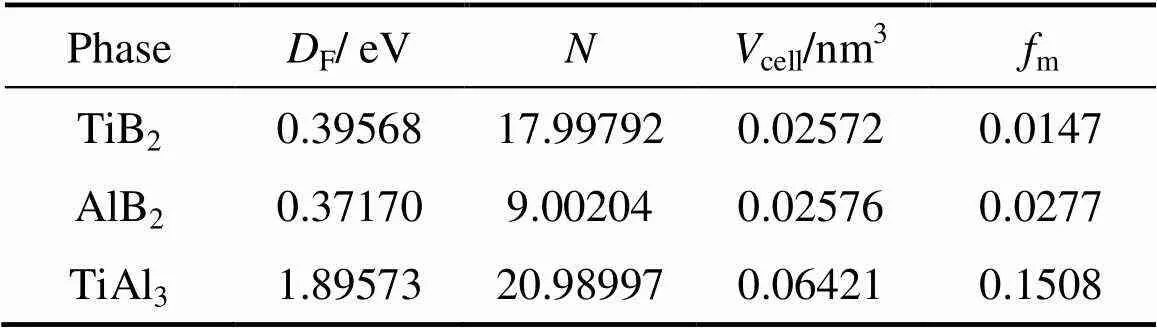
表3 物相费米能级处态密度值、总价电子数、晶胞体积以及金属性参数

2.3 热力学性质

图3所示为零压条件下计算所得TiB2、AlB2和TiAl3的定容摩尔热容c与熵在0~1200 K随温度的变化关系。图3(a)显示在室温(300 K)条件下3种物相的c分别为48.715、47.878和84.394 J/(mol∙K)，随着温度升高，3种物相的热容均有不同程度的增大。0~300 K的低温条件下，热容主要受到晶内原子热振动的影响，故在此阶段3种相的c随着温度的升高而迅速增大，服从德拜3定律；当温度升至300 K以上时，热容增速开始减小，但TiAl3的热容增速仍然高于两种硼化物；而与绝大多数固体在高温下的情况相同，在＞1000 K的高温区域内，3种物相内部非简谐效应被抑制，c增速逐渐放缓并趋近于各自的Dulong-petit极限。在0~1200 K温度范围内，两种硼化物粒子热容变化情况几乎一致，而这可能是由于两种物相晶型相同，内部原子的振动细节相似而造成的。进一步考察高温区域(900~1200 K)，TiB2和AlB2的热容与温度大致呈线性关系，且前者热容始终大于后者。

表4 TiB2、AlB2和TiAl3的体弹模量B0以及其对压强的一阶导数B'

1) Cal: Calculated; Ref: Reference; Exp: Experimental.

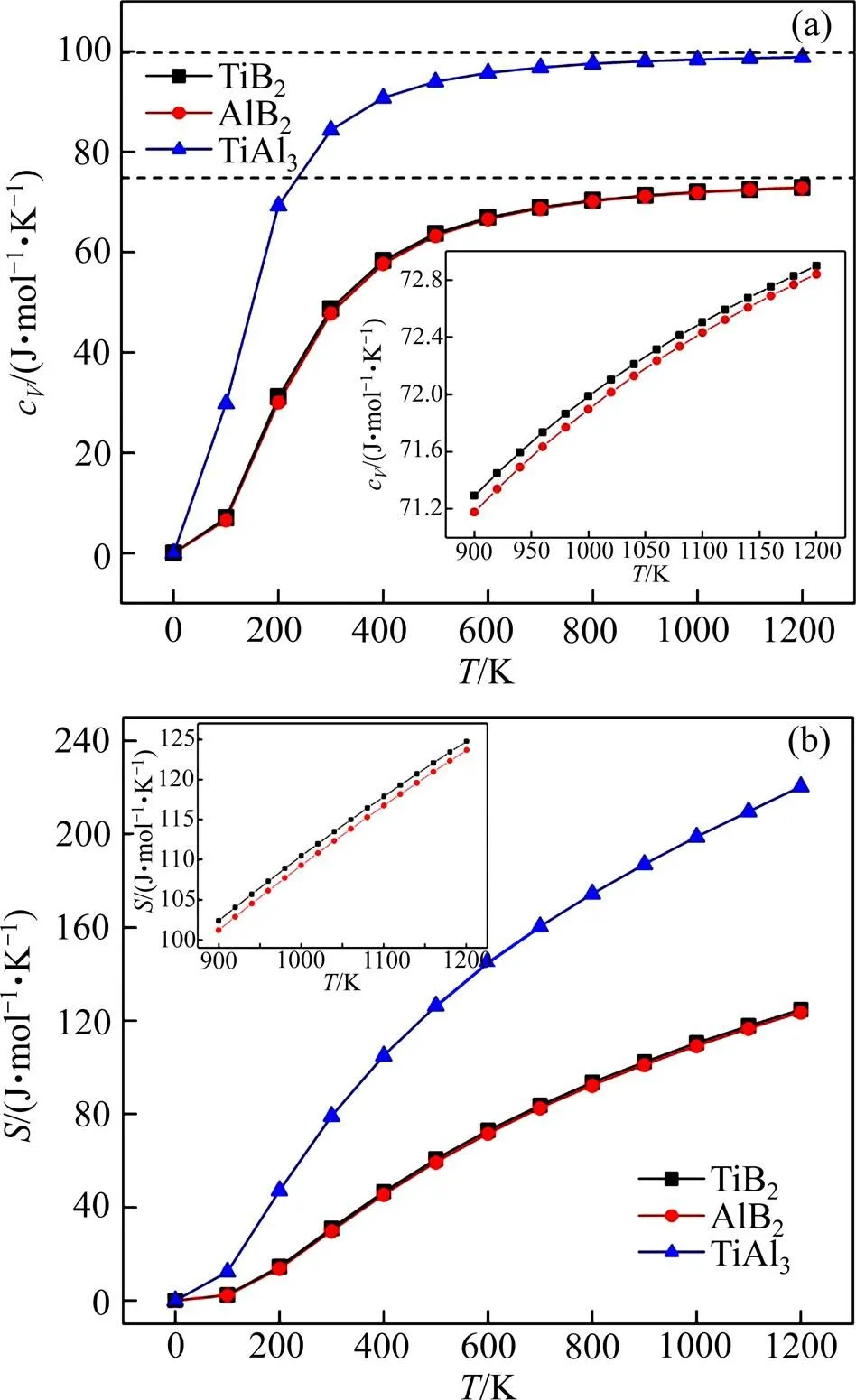
图3 TiB2、AlB2与TiAl3的热容cV与熵S的关系

图3(b)显示出零压条件下TiB2、AlB2与TiAl3的熵随温度的变化情况。可以看出在100~500 K温度范围内，TiAl3的熵值随温度的升高而剧烈增大。当温度继续上升时，熵增速率放缓(可以预计当温度高于某个值后，熵会逐渐趋于一个极限值)；而TiB2和AlB2的熵值增大速率低于TiAl3，且当＞200 K后，熵增速率比较恒定。从900~1200 K高温区内变化情况来看，TiB2的熵值大于AlB2，且两种硼化物的熵值与温度基本呈线性增加的关系。900 K时，TiB2、AlB2和TiAl3的熵分别为102.367、101.191和187.088 J/(mol∙K)。

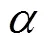
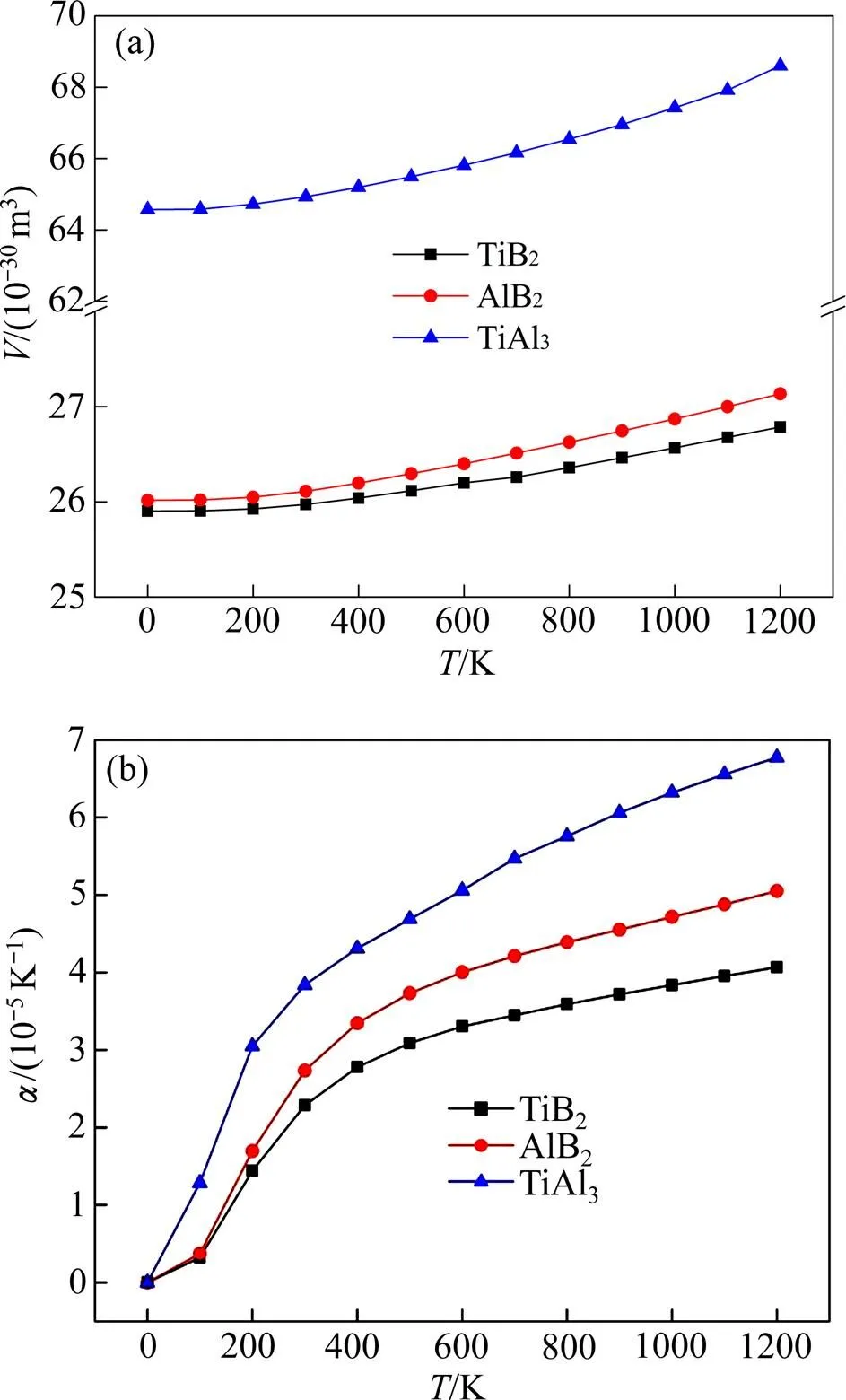
图4 TiB2、AlB2和TiAl3的热平衡体积V与热膨胀系数随温度的变化

采用氟盐法制备Al-Ti-B时，铝熔体与混合氟盐(K2TiF6和KBF4)之间发生的反应以及最终得到的物相组成可以从以上计算结果加以分析：低温熔炼时，具有较高热容与熵值的TiAl3需要一定的过热度才能形成，而K2TiF6加入铝熔体后立即与铝发生铝热反应并大量放热，使得熔体温度迅速升高，有利于大量生成TiAl3[34]。随着反应进行，熔体温度逐渐升高，呈金属键与离子键混合键合特性的TiAl3热稳定性较差而易熔解于铝液中，并使铝液中Ti的浓度升高，熔体中将存有大量的TiAl3块状小晶体；高温熔炼时，TiAl3熔解速率加快，少量未彻底溶解的TiAl3受到铝熔体中Ti元素的长程扩散的影响而择优生长，从而长大成为杆状或针片状。

TiB2的热容与熵值均高于AlB2，生成TiB2的自由焓更低，氟盐与铝液反应首先生成TiB2，剩余的KBF4与Al熔体才会生成AlB2，同时，高温条件下AlB2的热稳定性差于TiB2而处于亚稳定状态，由于Ti的存在，Ti将置换AlB2中的Al原子而逐渐形成(Al, Ti1−x)B2复合相直至TiB2[9]。因此，在高(Ti)/(B)的Al-Ti-B中间合金中AlB2含量远低于TiB2含量；在制备低(Ti)/(B)的Al-Ti-B(如Al-1Ti-3B)时，由于Ti含量相对较少，且Al熔体中添加过多的KBF4后黏度增大，在局部区域内Ti分布不均匀，因此，AlB2不能完全转化TiB2而存在部分AlB2在凝固过程中保留下来。

3 结论

1) 形成热与结合能的计算结果表明：3种金属间化合物的稳定性由大到小依次为TiB2、AlB2、TiAl3。TiB2的结合能低于AlB2，表明在Al-Ti-B中间合金中TiB2更加稳定；

2) 电子结构分析表明：3种物相的离子性与金属性由大到小依次为TiAl3、AlB2、TiB2。TiAl3与AlB2的键合特性以离子键为主，而TiB2键合特性以B 2p与Ti 3d轨道态电子杂化的共价键为主；

3) 准简谐德拜模型计算显示：TiB2、AlB2和TiAl3的定容摩尔热容与熵随温度升高而不同程度地增大，通过计算热膨胀系数发现3种物相的热稳定性由大到小依次为TiB2、AlB2、TiAl3。

[1] AURADI V, KORI S A. Influence of reaction temperature and reaction time for the manufacturing of Al-Ti-B (Ti:B=5:1, 1:3) master alloys and their grain refining efficiency on Al-7Si alloys[J]. Transactions of the Indian Institute of Metals, 2012, 65(6): 637−645.

[2] BIROL Y. An improved practice to manufacture Al-Ti-B master alloys by reacting halide salts with molten aluminium[J]. Journal of Alloys and Compounds, 2006, 420(1/2): 71−76.

[3] JONES G P, PEARSON J. Factors affecting the grain-refinement of aluminum using titanium and boron additives[J]. Metallurgical and Materials Transactions B, 1976, 7(2): 223−234.

[4] 李 贺, 柴丽华, 马腾飞, 陈子勇. 高温熔体反应法制备Al-5Ti-1B细化剂[J]. 材料工程, 2017, 45(2): 39−45. LI He, CHAI Li-hua, MA Teng-fei, CHEN Zi-yong. Synthesis of Al-5Ti-1B refiner by melt reaction method[J]. Journal of Materials Engineering, 2017, 45(2): 39−45.

[5] KORI S A, MURTY B S, CHAKRABORTY M. Development of an efficient grain refiner for Al-7Si alloy and its modification with strontium[J]. Materials Science and Engineering A, 2000, 280(1): 58−61.

[6] YU L, LIU X. The relationship between viscosity and refinement efficiency of pure aluminum by Al-Ti-B refiner[J]. Journal of Alloys and Compounds, 2006, 425(1/2): 245−250.

[7] 肖政兵, 邓运来, 唐建国, 陈 祺, 张新明. Al-Ti-C与Al-Ti-B晶粒细化剂的Zr中毒机理[J]. 中国有色金属学报, 2012, 22(2): 371−378. XIAO Zheng-bing, DENG Yun-lai, TANG Jian-guo, CHEN Qi, ZHANG Xin-ming. Poisoning mechanism of Zr on grain refiner of Al-Ti-C and Al-Ti-B[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(2): 371−378.

[8] 廖成伟, 陈闻天, 陈 欢, 付建平, 潘春旭. 原料添加顺序对氟盐法制备Al-Ti-B中间合金的影响[J]. 中国有色金属学报, 2016, 26(1): 204−211.LIAO Cheng-wei, CHEN Wen-tian, CHEN Huan, FU Chun-ping, PAN Chun-xu. Effect of feeding order on preparation of Al-Ti-B master alloy by fluoride salt method[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(1): 204−211.

[9] FJELLSTEDT J, JARFORS A. On the precipitation of TiB2in aluminum melts from the reaction with KBF4and K2TiF6[J]. Materials Science and Engineering A, 2005, 413(6): 527−532.

[10] MIRKOVIC D, GROEBNER J, SCHMID-FETZER R, FABRICHNAYA O, LUKAS H L. Experimental study and thermodynamic re-assessment of the Al-B system[J]. Journal of Alloys and Compounds, 2004, 384(1/2): 168−174.

[11] HERRING C. A new method for calculating wave functions in crystals[J]. Physical Review, 1940, 57(12): 1169−1177.

[12] KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects[J]. Physical Review, 1965, 140(4A): A1133/A1138.

[13] XIE Y P, WANG Z Y, HOU Z F. The phase stability and elastic properties of MgZn2and Mg4Zn7in Mg-Zn alloys[J]. Scripta Materialia, 2013, 68(7): 495−498.

[14] PERDEW J P, BURKE K, ERNZERHOF M. ERRATA: Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865−3868.

[15] MONKHORST H J. Special points for Brillouin-zone integrations[J]. Physical Review B Condensed Matter, 1976, 16(4): 1748−1749.

[16] BLANCO M A, FRANCISCO E, LUAÑA V. GIBBS: Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model[J]. Computer Physics Communications, 2004, 158(1): 57−72.

[17] FLÓREZ M, RECIO J M, FRANCISCO E, BLANCO M A, PENDÁS A M. First-principles study of the rocksalt-cesium chloride relative phase stability in alkali halides[J]. Physical Review B, 2002, 66(14): 144112−144123.

[18] WANG M. The investigation of dependences of mechanical and electronic properties of TiB2on pressure using the first-principles method[J]. Physica Scripta, 2014, 89(11): 115702−115714.

[19] DUAN Y H, SUN Y, GUO Z Z, PENG M J, ZHU P X, HE J H. Elastic constants of AlB2-type compounds from first-principles calculations[J]. Computational Materials Science, 2012, 51(1): 112−116.

[20] DUAN Y H, SUN Y, LU L. Thermodynamic properties and thermal conductivities of TiAl3-type intermetallics in Al-Pt-Ti system[J]. Computational Materials Science, 2013, 68(2): 229−233.

[21] MEDVEDEVA N I, GORNOSTYREV Y N, NOVIKOV D L, MRYASOV O N, FREEMAN A J. Ternary site preference energies, size misfits and solid solution hardening in NiAl and FeAl[J]. Acta Materialia, 1998, 46(10): 3433−3442.

[22] WU M M, JIANG Y, WANG J W, WU J, TANG B Y, PENG L M, DING W J. Structural, elastic and electronic properties of Mg(Cu1−xZnx)2alloys calculated by first-principles[J]. Journal of Alloys and Compounds, 2011, 509(6): 2885−2890.

[23] FJELLSTEDT J, JARFORS A E W, SVENDSEN L. Experimental analysis of the intermediary phases AlB2, AlB12and TiB2in the Al-B and Al-Ti-B systems[J]. Journal of Alloys & Compounds, 1999, 283(1/2): 192−197.

[24] KELLY P M, REN H P, QIU D, ZHANG M X. Identifying close-packed planes in complex crystal structures[J]. Acta Materialia, 2010, 58(8): 3091−3095.

[25] VAJEESTON P, RAVINDRAN P, RAVI C, ASOKAMANI R. Electronic structure, bonding, and ground-state properties of AlB2-type transition-metal diborides[J]. Physical Review B, 2001, 63(4): 33−41.

[26] BURKHARDT U, GURIN V, HAARMANN F, BORRMANN H, SCHNELLE W, YARESKO A, GRIN Y. On the electronic and structural properties of aluminum diboride Al0.9B2[J]. Journal of Solid State Chemistry, 2004, 177(2): 389−394.

[27] ZHANG M X, KELLY P M, EASTON M A, TAYLOR J A. Crystallographic study of grain refinement in aluminum alloys using the edge-to-edge matching model[J]. Acta Materialia, 2005, 53(5): 1427−1438.

[28] ZHANG H L, HAN Y F, WANG J, DAI Y B, SUN B D. An Ab initio molecular dynamics study on the structural and electronic properties of AlB2, TiB2and (Al,Ti(1−x))B2in Al-Ti-B master alloys[J]. Journal of Alloys and Compounds, 2014, 585(3): 529−534.

[29] LI Y, GAO Y, XIAO B, MIN T, FAN Z, MA S, XU L. Theoretical study on the stability, elasticity, hardness and electronic structures of W-C binary compounds[J]. Journal of Alloys and Compounds, 2010, 502(1): 28−37.

[30] SPOOR P S, MAYNARD J D, PAN M J, GREEN D J, HELLMANN J R, TANAKA T. Elastic constants and crystal anisotropy of titanium diboride[J]. Applied Physics Letters, 1997, 70(15): 1959−1961.

[31] LOA I, KUNC K, SYASSEN K, BOUVIER P. Crystal structure and lattice dynamics of AlB2under pressure and implications for MgB2[J]. Physical Review B, 2002, 66(13): 134101.

[32] GHOSH G, WALLE A V D, ASTA M. First-principles phase stability calculations of pseudobinary alloys of (Al,Zn)3Ti with L12, D022, and D023structures[J]. Journal of Phase Equilibria and Diffusion, 2007, 28(1): 9−22.

[33] OKADA Y, TOKUMARU Y. Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K[J]. Journal of Applied Physics, 1984, 56(2): 314−320.

[34] EL-MAHALLAWY N, TAHA M A, JARFORS A E W, FREDRIKSSON H. On the reaction between aluminium, K2TiF6and KBF4[J]. Journal of Alloys and Compounds, 1999, 292(1/2): 221−229.

First principle study of AlB2, TiB2and TiAl3in Al-Ti-B alloy

HUANG Yuan-chun1, 2, 3, SHAO Hong-bang1, XIAO Zheng-bing1, 2, 3, REN Xian-wei1, GUO Xiao-fang1

(1. Light Alloy Research Institute, Central South University, Changsha 410083, China; 2. State Key Laboratory of High Performance and Complex Manufacturing, Central South University, Changsha 410083, China; 3. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

The crystal structure, heat of formation, cohesive energy and electronic properties of AlB2, TiB2and TiAl3in Al-Ti-B system under 0 K condition were investigated by using first principles based on density functional theory, and the quasi-harmonic Debye model was performed to calculate the thermodynamic properties of these phases. The results show that the heat of formation and cohesive energy of AlB2, TiB2and TiAl3are both negative, which indicate that these phases possess structural stability, and the structural stability decreases in the order from big to little of TiB2, TiAl3, AlB2. The iconicity and metallicity of these compounds increase in the following sequence from big to little of TiAl3, AlB2, TiB2, and the dominant bonding in TiAl3and AlB2is ionic, while the bonding in TiB2is mainly covalent. The thermodynamic calculation results show that the thermal stabilities of the three phases decrease in the order from big to little of TiB2, AlB2, TiAl3, which can be used to illustrate the reactions between Al melt and fluoride salts when preparing Al-Ti-B by fluoride salt process.

Al-Ti-B alloy; first-principles; quasi-harmonic Debye model; structural properties; thermodynamics properties

Project(2015CB057305) supported by the National Basic Research Development Program of China

2017-06-05;

2017-09-20

HUANG Yuan-chun; Tel: +86-13507315123; E-mail: science@csu.edu.cn

10.19476/j.ysxb.1004.0609.2018.08.01

1004-0609(2018)-08-1491-08

TG146.2

A

国家重点基础研究发展计划资助项目(2015CB057305)

2017-06-05；

2017-09-20

黄元春，教授，博士；电话：13507315123；E-mail: science@csu.edu.cn

(编辑 李艳红)