基于机器视觉的河水表面流速估计

冯 全，张彦洪，赵晓刚



基于机器视觉的河水表面流速估计

冯 全1，张彦洪2，赵晓刚1

（1. 甘肃农业大学机电工程学院，兰州 730070；2. 甘肃农业大学水利水电学院，兰州 730070）

为了解决河水流速的视频测量需要投掷浮标、效率低等问题，提出了基于机器视觉的河水表面流速测量方法。采用高清摄像机拍摄河水流动视频，捕捉河水流动时表面产生的波浪运动。为了凸显这些细微的水面运动，利用帧差法计算运动显著性图。提取相邻2帧显著性图的SURF特征点，通过特征点匹配法找出相邻2帧的匹配点，将匹配点间的距离作为特征点在2帧图像间的运动距离。计算了多帧图像间特征点运动距离的直方图，该直方图具有单峰特征；通过对直方图进行曲线拟合准确地找到峰值对应的距离，将其作为最优的运动距离。最后结合帧间时间和根据小孔成像原理导出的速度公式估计出河水表面流速。为了验证该方法的有效性，用流速仪和该方法进行了对比试验。结果表明，该方法具有精度好、稳定性高和运算速度快的优点。在低、中速河流速度估计时，该方法最大变异系数为1.63%，与流速仪测量结果的最大相对误差仅为3.12%。对2组数据的一致性分析表明，2组数据的皮尔逊相关系数和斯皮尔曼相关系数分别为0.998和0.990，显示了该方法的速度估计值与流速仪实测值有良好的一致性。与已有的图像处理方法相比，不仅更为准确，而且耗时更短。研究可为用其他机器视觉处理算法估计复杂水面和高速水流提供参考。

河流；速度；视频；SURF特征；水流；帧差

0 引 言

人眼通过观察河水表面纹理细节的运动变化，可以察觉到水的流动，有经验的水文工作者甚至可以较精确地估计出河水的流速。流速测量是水文监测的重要工作之一，目前的流速测量依赖于各种仪器。常用的河水流速测量方法主要分为3类[1-4]：第1类是传统的流速仪测量法，其主要原理是通过水流带动旋桨转动，记录旋桨转速，通过一定的映射关系可算出流速；第2类是通过声学多普勒效应来测量流速，主要用于测量船，存在着设备和人力投入大、成本高的问题；第3类是非接触式，如微波多普勒测速仪，适合于测量流速较高的河水。近年来，一些研究者采用基于视频处理的流速测量方法[5-6]，如文献[6]通过跟踪水流视频中浮标的运动轨迹，结合摄像机标定来计算流速。但该类方法需要投掷浮标，无法对流速进行不间断实时监测。

传统模拟摄像机分辨率不高，加之要受到电磁传输干扰、A/D转换、D1画面的合成反交错等视频损伤，使得图像细节纹理丢失严重。用此类摄像机拍摄的流水视频中，流水运动产生的细节变化在视频上往往观察不清，因此传统的方法需要借助浮标或者示踪子，通过观察浮标的运动才能在图像中分析流水的运动。近年来，数百万乃至千万分辨率的高清数字摄像机在运动检测和目标跟踪方面应用越来越多，目前主要用于车辆违章抓拍[7-12]和行人跟踪[8-17]方面。借助高分辨率的摄像机也能较好地观测到水面波动的纹理细节，特别是含有泥沙的河水，水流表面运动模式比较明显。本文在利用高清摄像头拍摄序列图像（视频）的基础上，提出了基于机器视觉的非接触河水表面流速估计方法，通过在运动显著性图像上提取关键点的SURF特征来描述河水流动过程中产生波动的运动特征，然后通过特征点匹配的方法找到对应的运动点，计算出这些特征点的运动距离，以此估计水面的实际运动速度。

1 测量原理

摄像机最常用的模型是小孔成像模型。在该模型中，景物通过摄像机光轴中心投射到成像平面，如图1所示，采用三参数模型时，景物点（,,）投影到成像平面为成像点（,），再转换为图像点（p, p），则[18]：

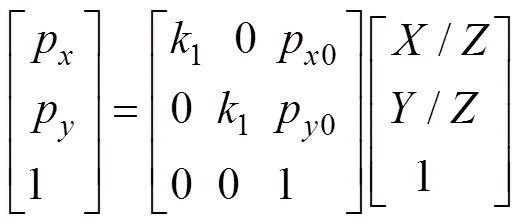
式中1=，是成像平面到图像平面的放大系数,为摄像机焦距；(p0,p0)是光轴中心在成像平面的交点的图像坐标。式（1）中的3个参数可以通过摄像机标定得到[18]。

注：为景物点，为其在图像平面的像点，为摄像机焦距。

Note:,anddenote object point, image point and focal length, respectively.

图1 小孔成像原理

Fig.1 Principle of pinhole imaging

由文献[18]可知，当景物点在垂直于光轴的景物平面时（该平面平行于图像平面），景物平面的一点从1(1,1,)运动到2(2,2,)时，在图像平面上对应点从1(p1,p1)运动到2(p2,p2)，其关系满足：

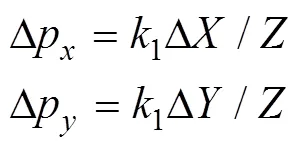
在测量河水表面流速时,摄像机镜头垂直于水面,水面可视为一平面。通过测量流水视频中的特征点的运动速度、水面到摄像机距离以及参数1可估计出河水表面的实际流速。

2 基于视频的表面流速估计

文献[19]采用模板匹配的方法来估计流速，需要先在前一帧图像上提取大小合适的区域作为模板以便在后一帧图像上进行模板匹配。但这种方法提取的模板数量和匹配上的区域数量较少，水面波动较大、流速较高时流速估计的偏差与方差都比较大。而本文提取图像的局部特征点来匹配，在各种流速的视频上均能提取出更多数量特征点，匹配点数量也较多；本文还采用特征点运动距离的众数而不是距离平均来求流速。这些措施使得流速估计结果更加可靠。图2给出了本方法估计河水表面流速时的流程图。

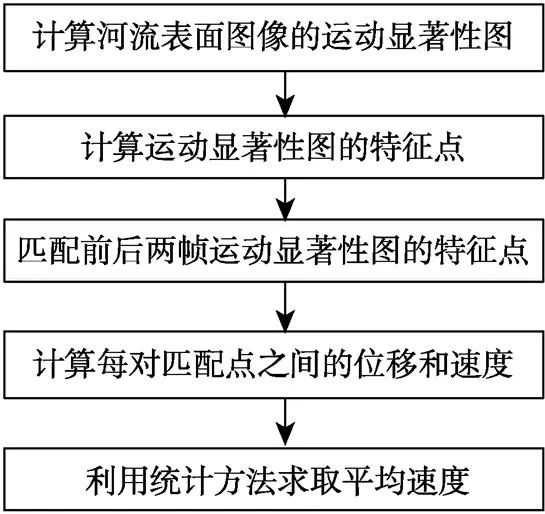
图2 河水表面流速估计的流程图

2.1 运动帧差图

车辆或行人运动检测时，运动目标和背景差异非常大，因为作为背景的路面或建筑是不动的，且颜色、形状与待检的运动目标也有很大差别。但在河流表面，水面作为整体是一起运动的，在完全平静而清澈的水面，视觉几乎无法察觉出水的运动。只有在河水有一定含沙量且水流运动不稳定，能够形成一定波浪，它们与周围均匀水面对光照有反射差异时，才能通过视觉感知水的流动，从而判断流速。波浪与周围均匀水面属于同一物质，很多情况下，即便是在高清摄像机拍摄图像中其差异也不是很明显，图3a和3b分别给出了这样的例子（视频的一帧原图和对应的灰度图）。这种情形给从河面图像中检测运动特征点造成了很大困难，如图3d中计算SURF特征点时，只能找到很稀疏的若干点，造成在相邻帧上进行特征点匹配时数量太少，无法鲁棒地估计运动速度。本文的解决思路是利用波浪运动造成连续2帧图像的差异放大运动区域，生成运动帧差图。设视频中当前帧为I（灰度图，=1,2,…），前一帧为I-1，则时刻的运动帧差图M计算如下：

（3）

式中2、3为预设系数，1为预设阈值。通过给2设置大于1的值，可给予运动显著区域的像素较大的系数，突出运动部位。

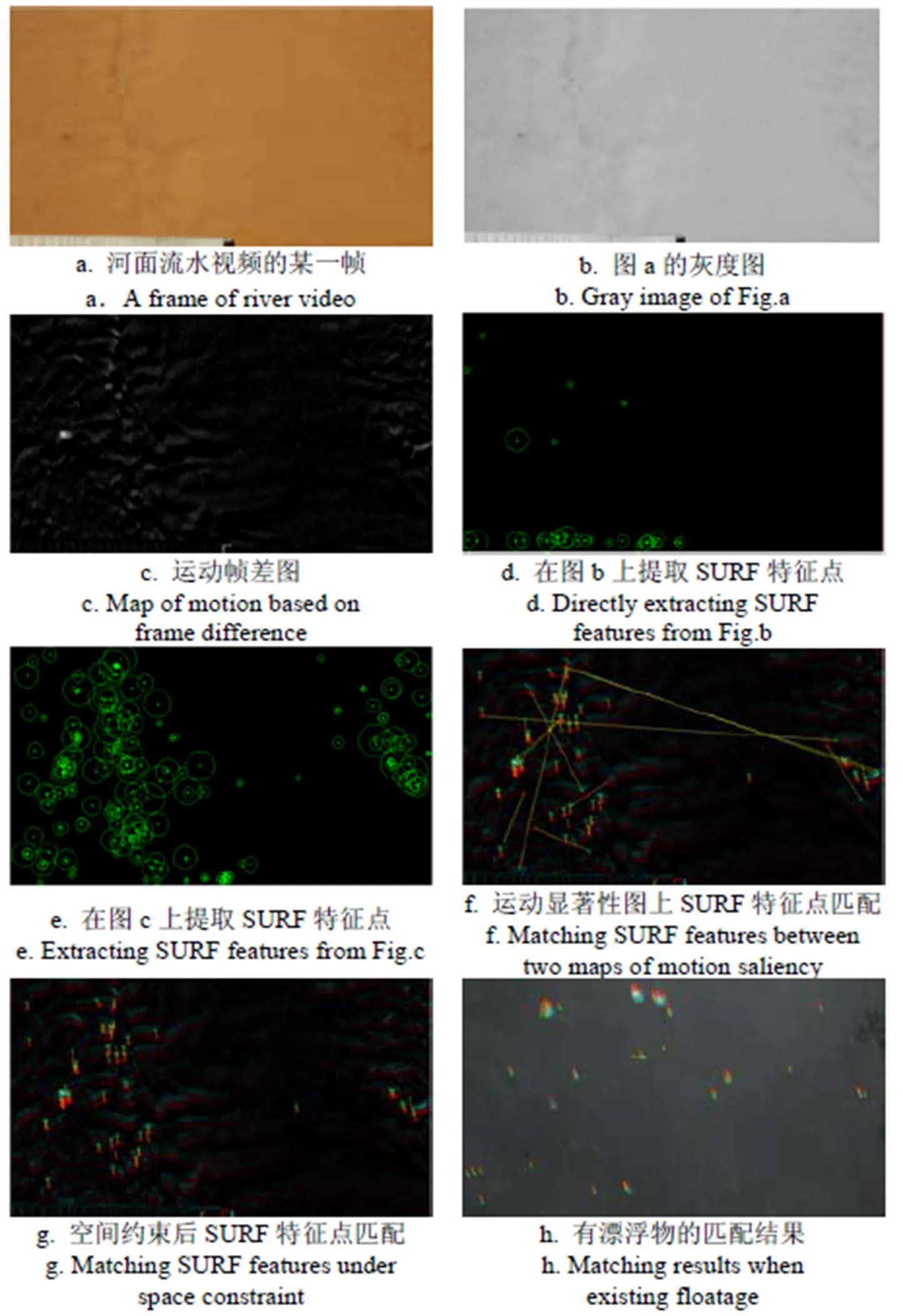
图3 SURF特征点的提取与匹配实例

2帧图像相减后，对于视觉无法感知运动的均匀水面，其对应值接近于0；对于视觉可以感知的运动波浪，由于连续2帧图像中其位置不同，其对应值较大。这种差异的增大为后续鲁棒地提取更多数量的特征点提供了基础。图3c是在图3b上计算出的运动帧差图，可以看出图中对应于原图，运动的波浪部分被很好地凸显出来。

2.2 运动特征点的提取与匹配

在机器视觉的文献中已经提出来很多特征点（关键点）的提取方法以及特征描述方法[20]，如SIFT描述子[21]、SURF描述子[22]、GIST算子[23]等。其中SURF是机器视觉中一种常用的局部特征描述算子[24-26]，用来描述某点周围空间的特征，将特征表述为一个特征向量，具有对图像缩放、旋转、甚至仿射变换保持不变性的图像局部特征描述算子的特点。试验表明SURF特征描述算子能很好地描述河流运动所产生的波纹，并且计算速度快。故本文在运动显著性图中提取特征点的SURF特征描述算子来表示运动特征，基本计算步骤如下：

1）通过Hessian矩阵，找出图像上的特征点；

2）构建尺度空间，定位特征点；

3）基于Harr小波提取特征点描述子。

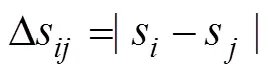
图3f给出了相邻运动显著图上特征点匹配的例子，其中2个有连线的点表示一对匹配点，可以看到出现了部分长距离匹配点，显然这是错误的匹配。为了进一步提高匹配的可靠性，还应考虑运动的空间约束。因为流水的速度通常并不很快，图像中的特征点在有限时间内的运动位移是有限的，因此m的对应点m位置只能出现在其周围一定空间内。这样，可根据预先设定的空间约束条件进一步删除部分错误匹配的点。若记d=|m-m|为2匹配点的坐标距离，则它们之间的空间约束条件为：2≤d≤3，2和3为预设的阈值，其值与流速、图像分辨率、摄像机高度等有关，在本文的试验条件下，2和3分别为设定为5和100像素，能满足滤去部分误匹配点，而基本不会丢掉正确匹配点的要求。图3g给出了在空间约束条件下计算出的匹配情况，可以看出效果比图3f好，更符合人的视觉感知。

河面中常有一些漂浮物，可以近似为刚体，在运动跟踪时起到了示踪子的作用，其运动形态比波浪更好检测。图3h给出了有漂浮物时运动点匹配的例子。

2.3 表面流速的估计

在相邻2帧运动显著性图上可以找到多对运动匹配点，每对点的运动距离并不相同，说明各点速度并不相同，这反映了摄像机视场内河面各点运动并不是一致的。此外，从图3g也可以看出，在2帧运动显著性图上找到的匹配点对在视场中分布并不均匀，它们能否代表整个视场的流速并不确定。但是如果在一段时间内将多帧图像上的匹配点对累积绘制在1张图上，则可以看出视场中匹配点对是基本均匀分布的，图4绘制了某段视频多帧运动显著性图上的匹配点对的累积分布情形。为了得到可靠的流速，本文并不计算单个特征点在2帧之间的速度，而是求视场内河面一段时间的平均流速的最优估计。即按照2.2节的方法估计出（试验中取100）帧运动显著性图以及所有相邻2帧上匹配特征点的最优运动距离后*后，在图像上平均流速的最优估计值*为

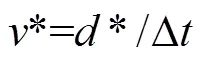
注：图中的大方框区域是对小方框区域的放大。

Note: In the figure, the large box area is an enlargement of the small box area.

图4 多帧运动显著图上SURF特征点累积分布图

Fig.4 Accumulated distribution of SURF features through multiple maps of motion saliency

为了得到*，以运动距离为横轴，落在某段距离范围内的点对数为纵轴，进行直方图统计。发现一段时间内各特征点对的运动距离密集分布在一定范围内，直方图通常呈现单峰分布，接近于正态分布。图5绘出了在某段河流视频中连续100帧运动显著性图上的相邻图匹配点位移－频次直方图，横坐标的单位是像素。本文取直方图中峰值处对应的横坐标距离为运动距离的最优估计，这相当于采用距离的众数作为估计依据。对大量直方图的观察发现，虽然大部分直方图呈单峰性，但会出现下面的3种情形：1）部分直方图的偏度不为0；2）有些直方图峰值处较为平坦；3）有些可能出现相邻双峰。此外受直方图坐标横轴统计间隔精度影响，即便是单峰，也不能在直方图上对峰值处准确定位。为了解决以上问题，本文采用了曲线拟合，即计算出直方图后，再用如下高斯曲线对其进行拟合：

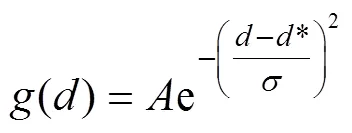
式中为匹配特征点的运动距离（像素），()表示对直方图的拟合高斯曲线，为其标准差，是其高度。

通过曲线拟合得到运动距离最优估计*后，代入式（4）可计算出视频中特征点的平均运动速度，也就是图像上流速的估计值。再利用式（2）和摄像机参数可以计算实际流速。由于运动距离是相对位移，且本文不考虑运动方向，故河水表面平均流速*（m/s）估计公式可简化为：

*=*/1（6）

式中为摄像机镜头到水面距离，m。

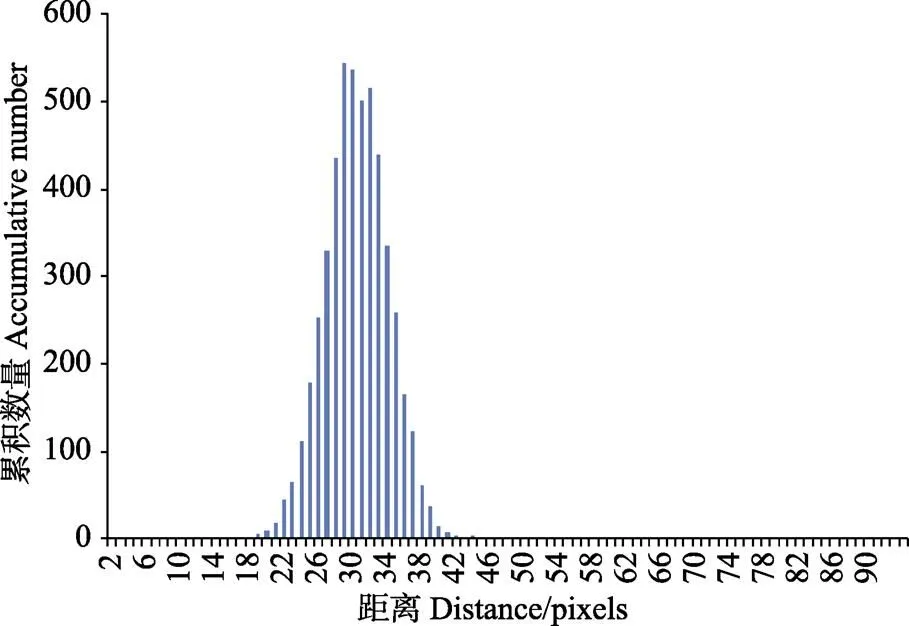
图5 距离直方图示例

3 案例及结果分析

3.1 试验设备及参数设置

试验中视频采集使用的摄像机为佳能公司EOS1200D，镜头采用EF 75-300 mm Ⅲ，拍摄视频的图像尺寸为1920×1088像素，帧率为25。视频图像处理过程是在惠普笔记本上完成（Intel i5-5200U CPU，@2.20 GHz，2 201 MHz，双核，4 GB内存，windows10操作系统），算法运行环境是matlab 2016a。水流测量仪型号为LS1206B型旋浆式流速仪（生产厂家：北京宏信恒测科技有限公司），涉水测量方式为侧杆安装，液晶屏读数，测速范围0.05～8 m/s，相对误差的绝对值≤5%，全线相对均方差的绝对值≤1.5%。

试验中参数1需要通过摄像机标定计算得到。2取1.5，3设置为1，即对运动显著区域的像素值给予一定放大，而对于非显著性区域的像素值则保持原值。为了选择合适的阈值1，本文在8次试验拍摄的视频中随机挑选8帧图像，对人工判断图像中没有明显运动的区域进行截图，计算出这些截图的像素平均标准差=1.04，将1设置为3。由于试验中摄像机高度距水面实际距离大约在2～3 m之间，在设定的不同焦距下，从视频计算出的运动显著性图中，特征点在2帧之间运动距离的众数基本在20～60像素，简单地将空间约束条件的2个阈值设为：2=5像素，3=100像素，以滤除部分违反空间约束的错误匹配点对。

3.2 河流速度测试与数据分析

为验证本方法的有效性，从2016年7月—2017年10月间的晴朗天气条件下，在黄河兰州段的河口至七里河黄河大桥之间的不同地点，拍摄了8段不同流速的水流视频，流速范围从低速到中速，并用流速仪同步测量了视场中心的流速作为基准。选择视场中各点水流方向一致、稳定的河面进行拍摄，河面没有漩涡和耀斑。摄像机固定在倒L型悬臂的顶端，支架高度1.8 m，拍摄时支架固定于岸边，镜头光轴垂直于水面，摄像机距离水面的实际高度用悬臂上的铅垂线测定，用0.4 m×0.4 m的轻质方框对摄像机进行标定[18]。测量时，每隔1 min用流速仪记录1次摄像机视场中央的流速，共测10次。流速仪完全浸没于水中但尽量接近水面。为了不干扰摄像机视场，每次测量完，迅速将流速仪拽离。用于流速估计的视频只取水面没有流速仪的部分。视频序列图像分析时，每100帧运动显著性图计算1次流速，即每4 s输出1次估计值；每1 min为1个周期，输出15个估计值；10 min为1次完整测量，得到150个流速估计值。表1给出了8次测量中流速仪和本文的视频测量结果的对比。本文方法测定的8种流速值与流速仪测定值的相对误差（RE，见表1）在1.39%～3.12%之间，2组测定结果比较接近。本文方法的最大CV为1.63%，可见流速估计法数据分散性小、精密度高。在本文的测试范围内，随着流速的加快，本方法的相对偏差和标准差有所增大的趋势。这可能与下述原因有关：1）流速仪测量的是单点流速，而本文是面流速的整体估计，两者之间本来有一定偏差。2）随着流速增大，水面波动增大，不稳定现象有所加剧，水面各点速度不同，导致标准差增加。

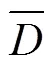
文献[30]采用模板匹配的方法来估计流速，需要先在前一帧图像上提取大小合适的区域作为模板以便在后一帧图像上进行模板匹配。表1给出了文献[30]和本文方法的比较，本文流速估计的CV和RE分别为1.46%和2.09%，而文献[30]分别为2.63%和2.88%，本文方法比文献[30]的方法分别减小了44.5%和26.9%。而在计算耗时方面，在本文计算的环境下，8次流速估计的平均时间为1.35 s，只有文献[30]（平均耗时30.3 s）的4.4%。本文方法与文献[30]相比有以下的优点：1）后者对作为模板的区域大小有一定要求，区域太大匹配速度慢，太小则不够稳定，故提取出的模板数量和匹配上的区域数量都较少，对于水面波动较大、流速较高时流速估计的偏差与方差都比较大；而本文方法是提取图像的局部特征点来匹配，在各种流速的视频上均能提取出更多数量特征点，匹配点数量也较多，故估计效果更加鲁棒。2）基于特征点的匹配比基于区域的模板匹配方法计算复杂度要小，这导致本文方法的计算速度得到了较大的提升，基本实现了流速的实时估计。3）后者对模板运动距离求平均来估计流速，对于有偏的距离分布，这种方法不够合理；本文对特征点运动距离直方图进行高斯曲线拟合后取高斯曲线的中心值作为最优运动距离，这相当于取多特征点运动距离的众数，更容易与流速仪的单点测量结果匹配。以上措施使得本文流速估计结果更加可靠，在表1的各项比较指标中，本文方法均优于文献[30]。

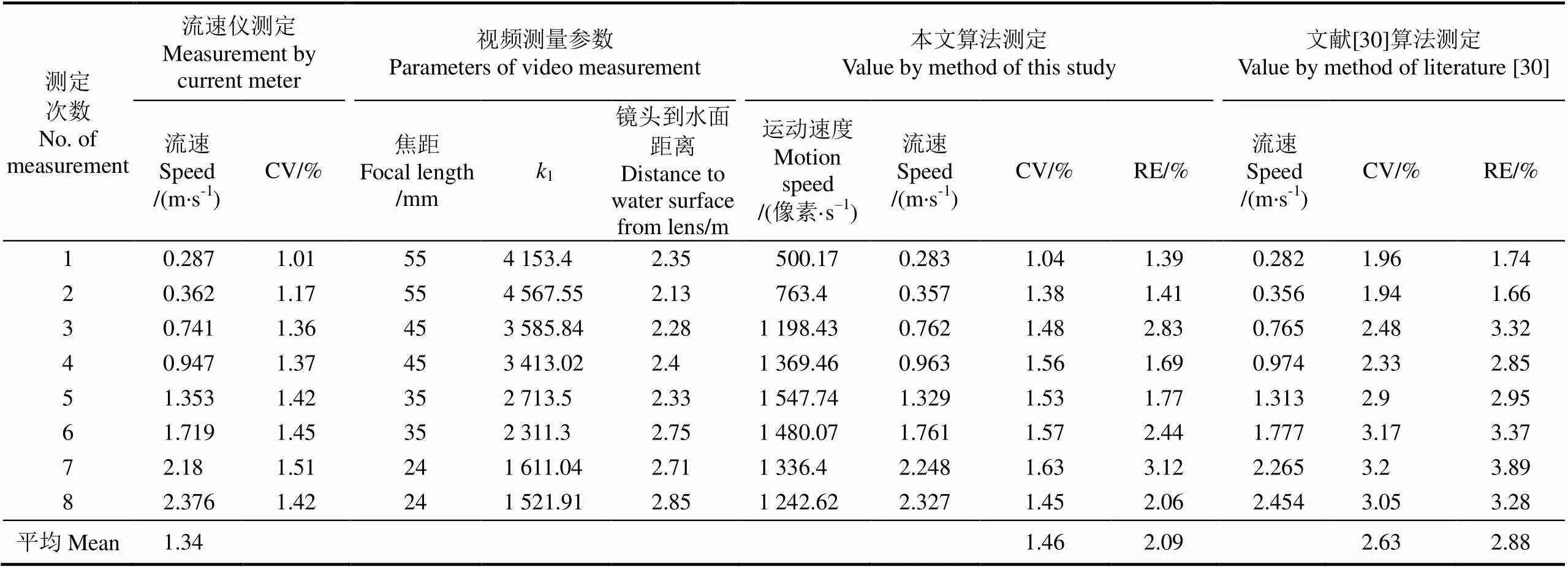
表1 流速仪与视频测量结果对比

注：流速仪流速为10 min测得流速的平均值；RE为估计值与流速仪测定值的相对误差；运动速度指图像平面上估计出的平均运动速度。

Note: Speed measured by current meter is average over 10 min; RE is relative error between estimator by this study and literature and that measured by current meter; Motion speed is the mean by the image plane.

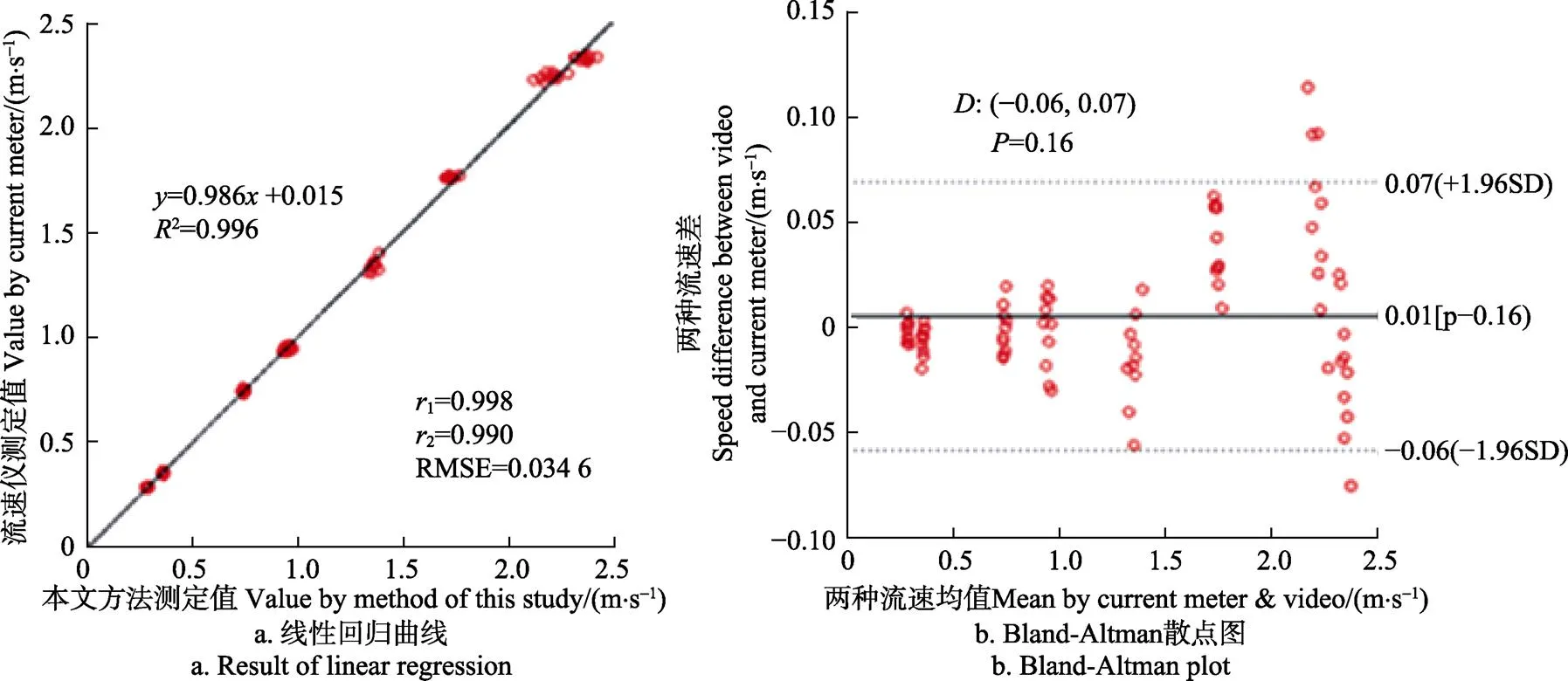
注：r1为皮尔逊相关系数，r2为斯皮尔曼相关系数，D为一致性限度，P为Bland-Altman回归显著性分析P值。

此外，本文还对文献[6]的浮子跟踪法的流速估计进行了试验，该方法采用卡尔曼滤波法跟踪浮子的轨迹，用若干帧间浮子的运动距离除以时间得到速度。试验条件和标定方法同前，为简单起见，本文用乒乓球代替浮子从摄像机镜头下漂过，重复5次，每次先用流速仪测得视场中心的流速，然后从视场外投掷乒乓球，使其自然漂入视场。试验中，选择从乒乓球完全进入视场对应的一帧到正要离开视场的那一帧来计算运动距离。流速仪5次实测的平均流速是0.315 m/s。本文算法的平均估计流速是0.319 m/s，变异系数为1.06%，与实测值的相对误差为1.27%；浮子法估计平均流速是0.321 m/s，变异系数为2.73%，与实测值的相对误差为1.90%。在浮子法测速试验中，无法控制每次测量时乒乓球的漂流路径，而乒乓球的不同漂流路径上的流速与视场中心流速差异会导致误差及变异系数增大。

本文虽然是对河水表面流速进行估计，其原理同样适用于明渠。但河水和明渠条件有所不同，通常河水携带泥沙量较多，浊度较大，水的波动比较明显，便于提取特征点。对于浊度类似的明渠，本方法有一定的实用性，但有些明渠中水较为清澈，肉眼难以观察明显波动，本文方法可能不适用。在以后研究中可以就什么浊度下的水流可以用本方法进行探讨，将本方法应用于明渠水流的测定。

4 结 论

传统的视频河水表面流速估计需要投掷示踪子来指示水流，费时费力，无法连续测量。本文采用高清摄像机捕捉河水流动时水面波动纹理的细节，通过计算视频的2帧图像之差获得运动显著性图，突出波动水纹的细节。在运动显著性图上计算特征点的SURF特征描述算子后，对前后2帧图像的特征点进行匹配，以获得特征点的运动距离；在获得大量运动数据后，采用统计方法估计出视频中特征点的最优运动速度，再联合摄像机标定来测算河水表面的实际流速。通过试验发现：本文方法的估计流速与流速仪实测结果相比，最大相对误差仅为3.12%，最大变异系数1.63%；采用多种一致性分析方法的得出本文的估计结果与实测值具有良好的一致性；与现有河水流速的视频估计方法相比，本文估计精度提高，计算时间仅为对比方法的4.4%。以上说明本文流速估计精度高，数据的一致性好，计算速度快。与传统方法相比，本方法的优点是不需要投掷浮标，可实现实时、连续测量，人力和设备成本低。

受条件限制，本文只在黄河兰州段部分河道上进行了试验，流速数据采集也只涵盖了低速到中速，对水面状态选择也有一定限制，如要求水流平稳，无耀斑和漩涡。这些限制条件主要为了减少噪声和程序的处理难度。不稳定水面上的耀斑，可在多帧图像中的某些区域来回闪动，会被程序误作为特征点；而水面漩涡内各点速度和方向都不相同，与无漩涡处的流速也不相同，可能在运动距离直方图上形成多个峰，而本文只拟合单峰，故可能导致曲线拟合时出现较大误差。但试验初步表明，本文提出的水流速度测量方法在受限条件下可以获得较高精度的测量结果，这为进一步采用其他机器视觉处理算法估计复杂水面和高速水流提供了参考。

[1] 盛森芝. 流速测量技术[M]. 北京：北京大学出版社, 1987.

[2] 王俊，熊明. 水文监测体系创新及关键技术研究[M]. 北京：中国水利水电出版社，2015.

[3] 于建华，杨胜勇，潘妮. 水文信息采集与处理[M]. 北京：中国水利水电出版社，2015.

[4] 王俊，陈松生，赵昕. 中美水文测验比较研究[M]. 北京：科学出版社，2017.

[5] 王兴奎，禹明忠，李丹勋, 等. 大范围表面流速场的图像处理系统及其同步实时测量方法: ZL 00130291. 4[P]. 2001-03-28.

[6] 韩予皖. 基于视频处理的河水流速监测系统设计[D]. 太原：太原理工大学, 2013. Han Yuwan. Velocity of River Flow Monitoring System Based on Video Processing[D]. Taiyuan: Taiyuan University of Technology, 2013. (in Chinese with English abstract)

[7] Cucchiara R, Piccardi M, Mello P. Image analysis and rule-based reasoning for a traffic monitoring system[J]. IEEE Transactions on Intelligent Transportation Systems, 2000, 1(2): 119－130.

[8] Schoepflin T, Dailey D. Dynamic camera calibration of roadside traffic management cameras for vehicle speed estimation[J]. IEEE Transactions on Intelligent Transportation Systems, 2003, 4(2): 90－98.

[9] Collins R T, Liu Y X, Leordeanu M. Online selection of discriminative tracking features [J]. IEEE Transaction on Pattern Anlysis and Machine Intelligence, 2005, 27(10): 1631－1643.

[10] 支晨蛟，唐慧明. 基于视频角点特征匹配的车速检测方法[J]. 计算机工程，2013，39(12)：176－180. Zhi Chenjiao, Tang Huiming. Vehicle speed detection method based on video corner feature matching [J]. Computer Engineering, 2013, 39(12): 176－180. (in Chinese with English abstract)

[11] Tran D, Yuan J, Forsyth D. Video event detection: From subvolume location to spatiotemporal path search [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(2): 404－416.

[12] 朱周. 复杂环境下基于视频的车辆跟踪算法研究[D]. 南京：东南大学，2015. Zhu Zhou. Research on Video Based Vehicle Tracking Algorithm in Complex Environment [D]. Nanjing: Southeast University, 2015. (in Chinese with English abstract)

[13] Munder S, Schnorr C, Gavrila D M. Pedestrian detection and tracking using a mixture of view-based shape-texture models[J]. IEEE Transactions on Intelligent Transportation Systems, 2008, 9(6): 333－343.

[14] Dollár P, Wojek C, Schiele B, et al. Pedestrian detection: an evaluation of the state of the art[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(4): 743－761.

[15] 苏松志，李绍滋，陈淑媛，等. 行人检测技术综述[J]. 电子学报，2012，40(4)：814－820. Su Songzhi, Li Shaozi, Chen Shuyuan, et al. A survey on pedestrian detection[J]. Acta Electronica Sinica, 2012, 40(4): 814－820. (in Chinese with English abstract)

[16] 吕敬钦. 视频行人检测及跟踪的关键技术研究[D]. 上海：上海交通大学，2013. Lü Jingqin. Research on Important Issues of Video Pedestrian Detection and Tracking [D]. Shanghai: Shaihai Jiao Tong University, 2013. (in Chinese with English abstract)

[17] 文嘉俊. 运动目标检测及其行为分析研究[D]. 哈尔滨：哈尔滨工业大学, 2015. Wen Jiajun. Research on Moving Object Detection [D]. Haerbin: Haerbin Institute of Technology, 2015. (in Chinese with English abstract)

[18] 徐德，谭民，李原. 机器人视觉测量与控制[M]. 第3版. 北京：国防工业出版社，2016.

[19] Tuytelaars T, Mikolajczyk K. Local invariant feature detectors: A survey [J]. Computer Graphics and Vision, 2007, 3(3): 177－280.

[20] Lowe D G. Distinctive image features from scale-invariant key points [J]. International Journal of Computer Vision, 2004, 60(2): 91－110.

[21] Bay H, Ess A, Tuytelaars T, et al. Speeded up robust features [J]. Computer Vision and Image Understanding, 2008, 110(3): 346—359.

[22] Oliva A, Torralba A. Modeling the shape of the scene: A holistic representation of the spatial envelope[J]. International Journal of Computer Vision, 2001, 42(3): 145—175.

[23] 张志斌，赵帅领，罗锡文，等. 基于SURF算法的绿色作物特征提取与图像匹配方法[J]. 农业工程学报，2015，31(14)：172—178. Zhang Zhibin, Zhao Shuailing, Luo Xiwen, etc. . Matching method of green crops based on SURF feature extraction [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(14): 172－178. (in Chinese with English abstract)

[24] 罗天健，刘秉瀚. 融合特征的快速SURF配准算法[J]. 中国图象图形学报，2015，20(1)：95—103. Luo Tianjian, Liu Binghan. Fast SURF key-points image registration algorithm by fusion features [J]. Journal of Image and Graphics, 2015, 20(1): 95—103. (in Chinese with English abstract)

[25] 邓集洪，魏宇星. 基于局部特征描述的目标定位[J]. 光电工程，2015，42(1)：58—64. Deng Jihong, Wei Yuxing. Location of object based on local feature descriptor [J]. Opto-Electronic Engineering , 2015, 42(1): 58—64. (in Chinese with English abstract)

[26] Bunce C. Correlation, agreement, and Bland-Altman analysis: Statistical analysis of method comparison studies [J]. Am J Ophthal, 2009, 148(1): 4—6.

[27] 李镒冲，李晓松. 两种测量方法定量测量结果的一致性评价[J]. 现代预防医学，2007，34(17)：3263—3266. Li Yichong, Li Xiaosong. Evaluation on different assessment methods of consistency of quantitative measurements [J]. Modern Preventive Medicine, 2007, 34(17): 3263—3266. (in Chinese with English abstract)

[28] Zaki R, Bulgiba A, Ismil N. Testing the agreement of medical instruments: overestimation of bias in the Bland-Altman analysis [J]. Prev Med, 2013, 57(3): S80—82.

[29] Shao Jun. Mathematical Statistics Second Edition [M]. NewYork: Springer, 2009.

[30] 赵晓刚，冯全，王书志. 一种基于帧间差分与模板匹配的河水表面流速测量方法[J]. 计算机应用与软件，2017，34(9)：68－71. Zhao Xiaogang, Feng Quan, Wang Shuzhi. Measuring surface velocity of river flow based on images of frame difference and template matching[J]. Computer Applications and Software, 2017, 34(9): 68－71. (in Chinese with English abstract)

Estimation of surface speed of river flow based on machine vision

Feng Quan1, Zhang Yanhong2, Zhao Xiaogang1

(1.730070,; 2.730070,)

The wave represents the motion of river flow. The surface speed of river can be estimated through motion analysis for the wave. In the paper, a method was proposed based on computer vision to estimate the surface speed of river directly. The method tried to capture the motion of wave caused by flowing river from the video. However, even taken by HD camera, the contrast between moving waves and even surface in an image is still not obvious since they are homogeneous and all moved as a whole. In order to enlarge details of the motion of waves, the map of motion saliency was calculated by the way of frame difference method. In the map, the key points were extracted and characterized by SURF features. These key points represented the most salient positions of waves. Through the point matching algorithm, a key point in one map and its counterparts in next map were searched. The correspondence between the 2 matched points indicated the motion of wave in the video and the distance between them was computed. In principle, with this distance and the parameters of camera, we could estimate the immediate speed of flow. However, the distance was noisy essentially. For robust and accurate estimation, we estimated the average speed instead of immediate speed. So, we calculated the histogram of the distances during the period of time. We found that most of these histograms appeared as uni-modal distribution. However, there existed some histograms which appeared with 2 adjacent peaks, or appeared with a flat peak. This resulted in the difficulty for estimation of distance accurately. To address the problem, we utilized the Gaussian curve to fit the histogram. The peak of the fitted curve could be searched accurately and its corresponding distance was viewed as the optimal estimation of average distance. Finally, with the speed formula derived from pinhole model, the optimal distance and the time between 2 maps, we could estimate the average surface speed of the river flow. To validate the availability of the proposed method, we compared the speeds estimated by our method with the baselines measured by the current meter. In our experimental setting, we selected gently surface for measurement task, without whirlpool and reflection. We conducted 8 measurements, with the speeds being limited between low and middle range. The experimental results showed that maximal relative error of speed between ours and the baseline was 3.12% while the min relative error only 1.39%, indicating good accuracy of our method. The min and max coefficient of variation was 1.04% and 1.63% respectively, showing high reliability. The correlation coefficients of Pearson and Spearman between our estimators and measured values were respectively 0.998 and 0.990. Bland-Altman regressionis 0.16, higher than 0.05 and in Bland-Altman scatter plot, most of points fell into the limits of agreement. These results showed that the flow speed estimated by our method had a good consistency with the baselines. In addition, our method was compared to the image processing method by previous literatures, the results showed that the time consumption was shortened by our study, which was only 4.4% of that of the literature, indicating that our method is faster than the previous method. In sum, this study provides an effective method for the estimation of flow speed of rivers with complex background.

rivers; speed; video; SURF feature; flow; frame difference

10.11975/j.issn.1002-6819.2018.19.018

TP391.41

A

1002-6819(2018)-19-0140-07

2018-02-04

2018-08-10

国家自然基金资助项目（61461005）；甘肃省水利厅科技计划项目（201776）

冯 全，四川隆昌人，教授，博士，研究方向：计算机视觉，农业工程。Email：fquan@sina.com

冯 全，张彦洪，赵晓刚.基于机器视觉的河水表面流速估计[J]. 农业工程学报，2018，34(19)：140－146. doi：10.11975/j.issn.1002-6819.2018.19.018 http://www.tcsae.org

Feng Quan, Zhang Yanhong, Zhao Xiaogang. Estimation of surface speed of river flow based on machine vision[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 140－146. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.19.018 http://www.tcsae.org