关于一道不定积分习题的多种解法分析

李媛媛

(江苏省南京林业大学应用数学系 210037)

大学数学教育阶段，高等数学是一门重要的基础课.课程一般分为三个部分：微积分学、解析几何和常微分方程.对于理工科学生来说，学好高等数学，理解透高等数学，才能在之后的专业学习中事半功倍.

不定积分是高等数学的一个教学重点和教学难点.不定积分的计算，方法灵活，技巧性强，解法多种多样.不定积分的计算中，我们主要使用的是第一类换元法，第二类换元法和分部积分法.学生在学习中往往感觉不定积分的计算很难掌握.教师在教学时，对某些例题采用多个解法来讲解，有利于学生的思维开拓，也使其能更好地理解解题的思路.同时我们对学生在做题时常常忽略的问题将着重分析，达到灵活使用多种积分方法的目的.

一、问题及解法

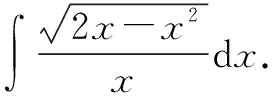
1.解法一 第二类换元法中的根式换元法的应用

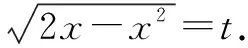
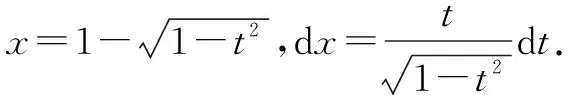
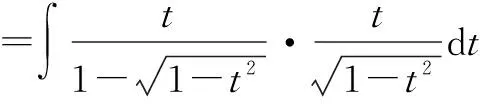
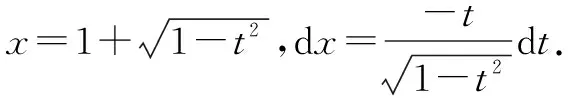
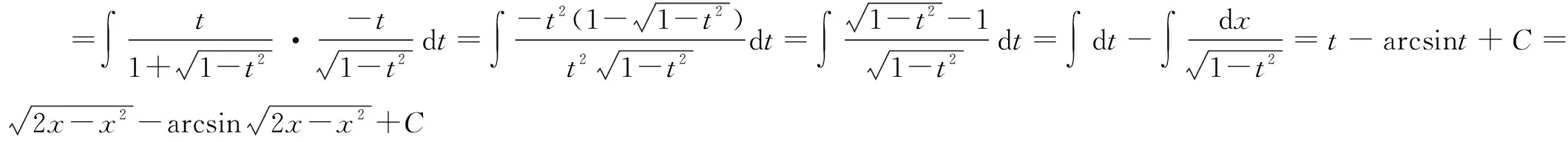
分析在含有根式的被积函数情况下，我们往往考虑第二类换元法中的根式代换法.我们知道换元法是不定积分计算时一个重要的工具.在使用换元法时，被积函数的定义域往往被忽略考虑.我们在求不定积分的时候，应该求得是被积函数在定义域上的不定积分，不能只考虑定义域的部分区间上的不定积分.在解法一中，我们发现被积函数的定义域需要被分割为两个区间去考虑.在不同的区间中，自变量x的表达式是不一样的.学生在考虑这个问题往往会只考虑解法中的一种情况，而忽略另一种.

2.解法二：第二类换元法的根式换元法与第一类换元法的综合运用

令：2x-x2=t.

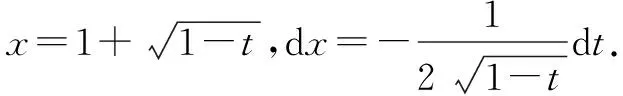
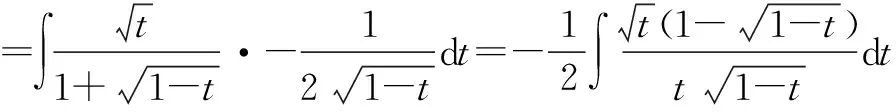
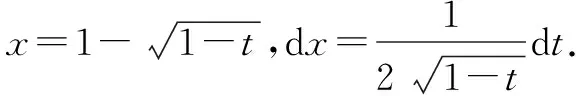
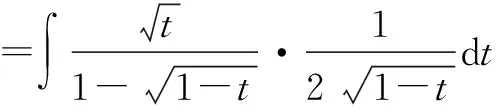
分析我们看到解法一与解法二都是同一个类型的根式换元法.学生在做不定积分的计算题时，时常会问这个问题：不定积分的计算太难了！使用换元法时，到底应该拿哪一部分的表达式来换元呢？我的回答是，多尝试！把你觉得可能的换元情况自己拿起笔算一算，看看能不能再继续算下去，能不能在换元后得到的被积函数是原函数容易计算的形式了.多动笔，多练习，才是学好不定积分的计算的必经之路.

3.解法三：第二类换元法的三角换元法的应用

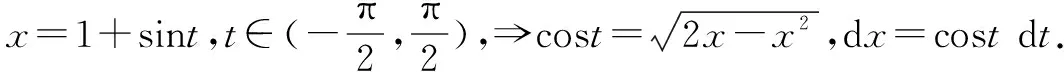
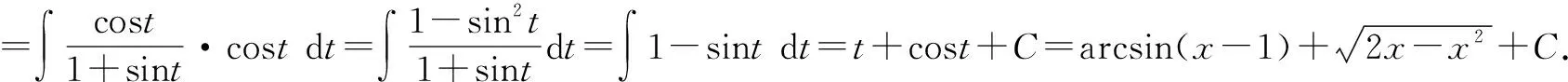
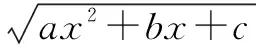
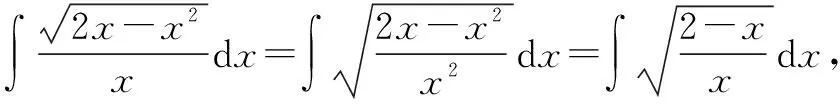
4.解法四：第二类换元法的根式换元法与分部积分法的综合应用

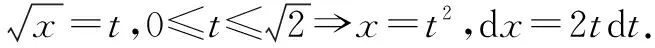
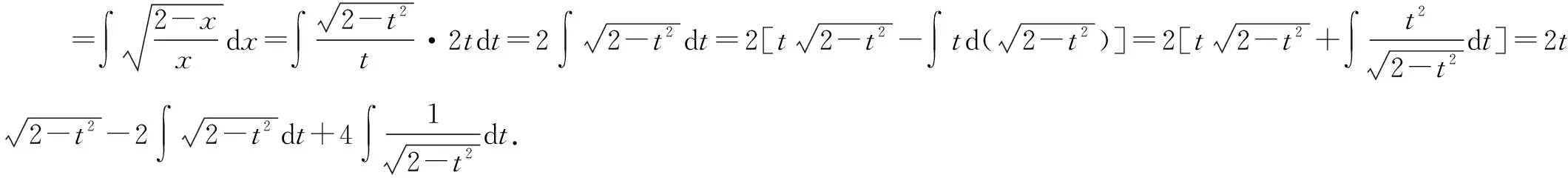
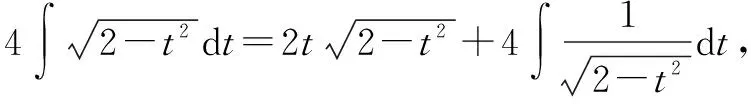
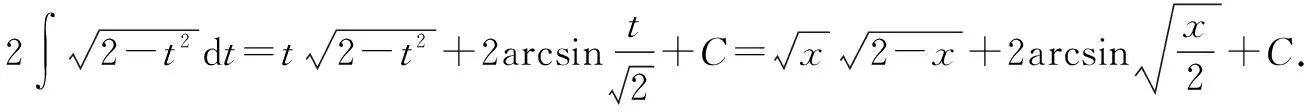
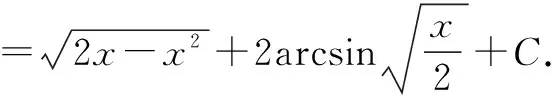
分析(1)在不定积分计算中，我们往往会对被积函数变形，以起到简化被积函数的目的.在函数的变形时，我们要使用的是恒等变换.恒等变形时需要大家注意前后函数的一致性，特别是在定义域上需要保持一致，必要时需要分情况考虑.

(2)不定积分计算的一个重要方法：分部积分法.其原理是函数四则运算求导法的逆运用.分部积分法的适用的被积函数有部分具体的情况.例如：幂函数和正(余)弦函数的乘积、幂函数和指数函数的乘积、幂函数和对数函数的乘积、指数函数和正(余)弦函数的乘积、幂函数和反三角函数的乘积等.我们在使用分部积分的方法时，要注意是否会出现循环形式.如果有循环公式出现，则可以使用解方程的方法将不定积分求出.解法四中便是使用了分部积分后，出现了循环形式，再求解不定积分.

5.解法五：第二类换元法的根式换元法和三角换元法的综合应用

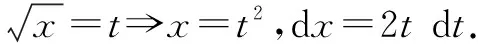
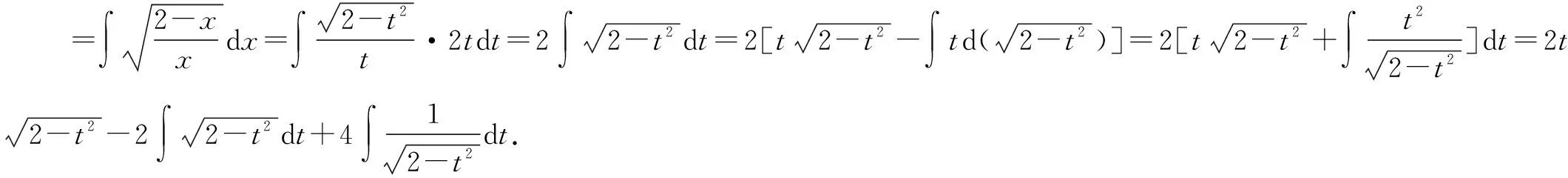
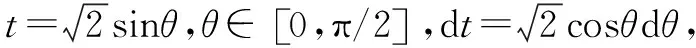
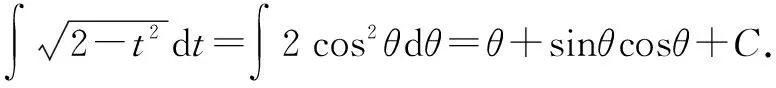
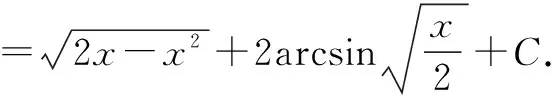
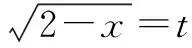
二、总结

本文给出了一道不定积分的多种解法.这些解法中结合了多种积分的方法.第一类换元法(凑微分法)、第二类换元法(根式换元法，三角换元法等)与分部积分法都融入解法中，充分体现了积分法的综合应用，拓宽了解题思路，对灵活掌握不定积分的计算方法有一定的启发作用.

我们在讲解不定积分的计算时，往往会采用一题多解的形式，来启发学生.但是要指出的是，我们的教学目标还是学生自己能解决不定积分的计算问题.我们讲授多种解题思路并不是要求学生每一种解法都会做，而是希望学生在拓宽思路的同时，能够选择自己“顺手的”，也就是熟练的方法来处理不定积分的计算.我们并不是要求大家寻求“新奇特”的解法，而是希望大家对常规的经典的不定积分计算，至少要能熟练掌握一到两种的常规做法.对于学生来说，掌握不定积分的计算最根本的还是充足的练习量.在练习中，体会多种解法的应用，从而才能灵活掌握多种积分的方法.

同时，我们也指出在计算不定积分的过程中，大家容易忽略的一些问题所带来的错误.一般容易出现的错误都在于换元法和函数变形时，对被积函数的定义域没有充分考虑，从而造成了被积函数的定义域的改变.所以在计算不定积分时，要注意在变量替换和函数变形时，要保证前后被积函数的定义域是前后对应的，不能扩大或是缩小了被积函数的定义域.