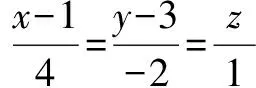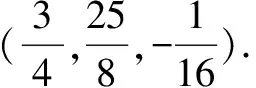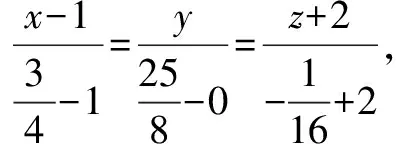一题多解及变式在解析几何教学中的应用

赵 燕

(江苏泰州学院数理学院 225300)

关于空间直线与平面的相关位置，两直线的相关位置及两平面的相关位置的题目千变万化，一般都可以一题两解，甚至一题多解.下面我们就书上的例题和课后习题来探究求解的一般思路及特殊方法，从而说明了在实际教学过程中，教师应该注重培养学生思维的广阔性和深刻性.

首先给出一道求平面方程的题目，见《解析几何》书上第134页的例1.

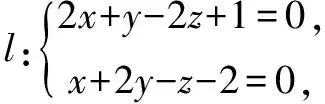
解设所求平面方程为l(2x+y-2z+1)+m(x+2y-z-2)=0，

即(2l+m)x+(l+2m)y+(-2l-m)z+(l-2m)=0.

由两平面垂直的条件得(2l+m)+(l+2m)+(-2l-m)=0，即l+2m=0，因此l∶m=2∶(-1).

所求平面方程为：2(2x+y-2z+1)-(x+2y-z-2)=0，即3x-3z+4=0.

可以发现，书上第120页的第3题的2小题事实上是上述例题的变式.

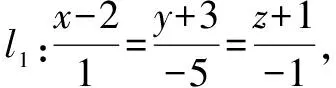
分析方法1： 类似于例1的解法，写出所求平面的方程，再利用所求平面的法向量与l2的方向向量垂直.

方法2：设所求平面π的法向量为n，利用点法式写出通过直线l1上一点(2,-3,-1)的所求平面π的方程，再利用π的法向量n与l1和l2的方向向量均垂直.

接下来探究求直线方程的题目，见《解析几何》书上第132页的第9题.

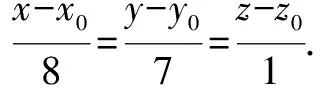
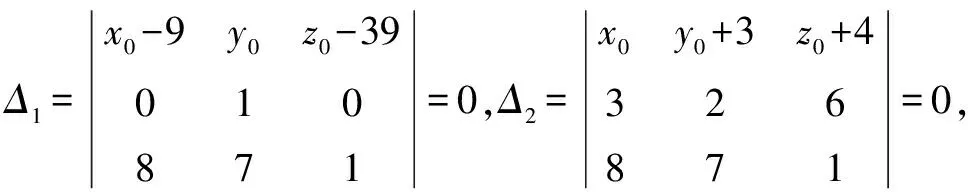
方法2： 设所求直线为l，因为l与直线l1平行，可设l的方向向量为v={8,7,1}.直线l2与l3的方向向量分别为v2={0,1,0}，v3={3,2,6}.在直线l2上设y=0，解得x=9,z=39.那么(9,0,39)为直线l2上一点.在直线l3上设x=0，解得y=-3,z=-4.那么(0,-3,-4)为直线l3上一点.因为所求直线l可以看作两平面的交线，其一是l与l2决定的平面，其二是l与l3决定的平面，所以两平面的方程分别为

《解析几何》书上第132页的第7题事实上是例2的变式.

分析设所求直线l的方向向量为v，直线l1的方向向量为v1={4,-2,1}，且过点M1(1,3,0)，平面π的法向量为n={3,-1,2}.

解方法1：所求直线l可以看作两平面π1和π2的交线，π1是通过点P(1,0,-2)且与平面3x-y+2z-1=0平行的平面，π2是P与l1决定的平面(过P点，以M1P和v1为方位向量)