含参不等式求解的思维方向
郭洪林
(黑龙江省哈尔滨市第三中学 150001)
含参不等式恒成立问题常与函数、方程、数列等知识交汇,又涉及到诸多的数学思想和数学方法,一直是解题的难点.本文根据自己对此类题型的求解体会,归纳出以下几种求解方法,希望提高学生解答此类问题的能力.
一、最值法
我们知道,要使不等式f(x)≥0恒成立,只要f(x)的最小值f(x)min≥0即可.因此问题转化为求出f(x)的最小值,再继续求解,得出参数的值(或范围).
例1 (2017全国卷Ⅱ21题(1))已知函数f(x)=ax2-ax-xlnx,且f(x)≥0,求a的值.
解易见f(x)的定义域是(0,+∞),因此f(x)≥0等价于g(x)=ax-a-lnx≥0恒成立.
观察易见g(1)=0,故x=1应是g(x)的一个最小值点.
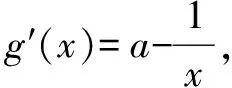

可见x∈(0,1)时,g′(x)<0,g(x)递减;x∈(1,+∞)时,g′(x)>0,g(x)递增.因此x=1是g(x)的最小值点,则有f(x)≥g(1)=0.
综上知a=1.
点评本解法中观察出g(1)=0是解题的关节点.上述求解的前半部分,利用特殊的g(1)=0是最小值,求出a=1;后半部分论证了a=1时,f(x)≥0恒成立.因此a=1是f(x)≥0的充要条件.
本例若观察不到g(1)=0,也可采用将a分类讨论来求f(x)的最小值,但是过程比较复杂.
二、分离参数
对于含参数a的不等式f(x,a)≥0,若能设法分离出参数a,化成a≥g(x)或a≤g(x)恒成立的问题,那么只要求出g(x)的最大值或g(x)的最小值,从而得到参数a的取值范围.
例2 (2008江苏卷14题)f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0成立,则a=____.
分析本题中参数a的“系数”x3的符号不确定,为了分离出参数a,需对x的符号进行分类讨论.
解(1)若x=0,则f(x)=1,显然对任意a的值,f(x)≥0恒成立.
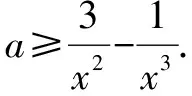
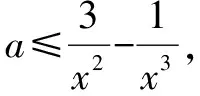
综合上述三种情况,要使x∈[-1,1]时不等式f(x)≥0都成立,得a=4.
三、变更主元
在含参数m的不等式f(x,m)>0中,受常规思维的影响,往往把它看成关于变元x的不等式来考虑,而这样的思维方式常常难以寻得解题思路,或囿于思路的复杂而陷入困境.此时若能及时调整思维方向,视已知范围的量为主元,常可使思维豁然开朗.
例3 若函数f(x)=mx2-mx-6+m对任意x∈[-2,2]都有f(x)<0成立,求x的取值范围.
分析本题所给是关于x的函数f(x),常规思路是首先要分m=0,m≠0考虑f(x)是否二次函数;而m≠0时,又要按m<0,m>0两种情况考虑相应抛物线开口方向;接着还要考虑对称轴、最值点位置情况.简直是太复杂了.注意到本题中的条件是m的范围[-2,2]是已知的,应充分利用这个条件,把已知函数式视为关于m的函数,就容易把握问题了.
解把题设函数视为关于m的函数,即g(m)=f(x)=(x2-x+1)m-6,m∈[-2,2].

四、数形结合
将不等式转化为形如f(x,m)>g(x,m),然后考察该式左、右两个函数图象之间的上下位置关系问题,使解题直观而易操作.
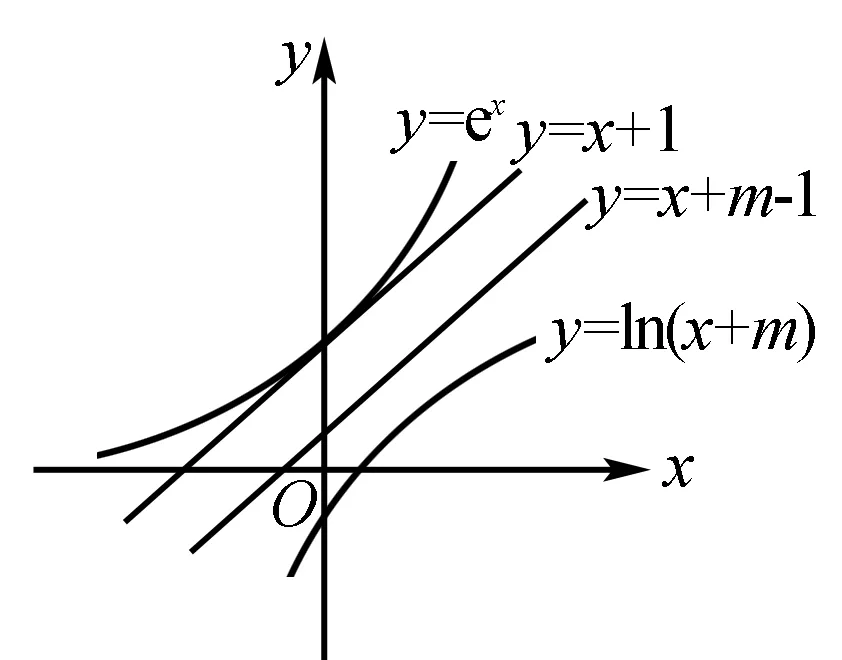
例4 (2013全国Ⅱ卷21题)已知函数f(x)=ex-ln(x+m).(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(2)当m≤2时,证明f(x)>0.
解(1)略.
分析要证f(x)=ex-ln(x+m)>0,即证ex>ln(x+m).
联想到课本上的两个不等式ex>1+x,lnx 证明设g(x)=ex-(x+1),g′(x)=ex-1.当x<0时,g′(x)<0;当x>0时,g′(x)>0.因此x=0是g(x)的最小值点,即g(x)≥g(0)=0,得ex≥x+1(取“=”时,x1=0)①. 当x<1-m时,h′(x)>0;当x>1-m时,h′(x)<0.因此x=1-m是h(x)的最大值点,有h(x)≤h(1-m)=0,也即ln(x+m)≤x+m-1(取“=”时,x2=1-m)②. 而当m≤2时,有x+1≥x+m-1,则由①和②有ex≥ln(x+m). ①和②同时取“=”的条件是x1=x2,即1-m=0,m=1;且x+1=x+m-1,得m=2.但m=1与m=2不能同时满足,故有ex>ln(x+m),即f(x)>0. 说明本例中的①和②两个不等式,其实就是人教版《数学选修2-2A》第32页B的1(3)、(4)两个不等式的变形推广.因此熟悉课本中的典型题目,并且明了题目的图形背景,这对我们开拓思维,理解题意,构建解题思路十分有益,常可化隐为显,化难为易.