苏通GIL综合管廊声传播特性仿真研究

李永亮，唐俊，党冬，闫晔，刘之方



苏通GIL综合管廊声传播特性仿真研究

李永亮1，唐俊2，党冬1，闫晔1，刘之方1

(1. 中国电力科学研究院有限公司，北京 100192；2. 苏州静声泰环保科技有限公司，江苏苏州 215638)

苏州-南通气体绝缘金属封闭式输电线路(Gas-Insulated metal-enclosed transmission Line, GIL)综合管廊工程是目前世界上电压等级最高、输送容量最大、技术水平最高的超长距离GIL创新工程。通过分析管廊内部结构，建立了其物理模型，根据声学理论，结合管廊布置方式提出两种计算模型，采用有限元方法对苏通GIL综合管廊的声场分布进行计算，并能为管廊内的故障声波定位提供参考。研究结果表明：对于非均匀声源，管廊的平面波截止频率在15 Hz附近。若声源频率低于15 Hz，声波在传播过程中快速转化为一维平面波，可采用“到达时间差法”(Time Difference of Arrival, TDOA)进行定位；如果声源频率高于15 Hz，则需对声波信号做进一步的时域和频域分析以确定适合的定位算法。

苏通GIL综合管廊；气体绝缘金属封闭式输电线路；电击穿；故障定位；有限元法

0 引言

气体绝缘金属封闭输电线路(Gas-insulated Metal-enclosed Transmission Line, GIL)是一种采用六氟化硫(SF6)或其它气体绝缘、外壳与导体同轴布置的高电压、大电流、长距离电力传输设备，具有输电容量大、损耗小、占地少、运行可靠性高、维护量小、寿命长、环境影响小等显著优点，尤其适合作为架空输电方式或电缆送电受限情况下的补充输电技术[1]。

苏州-南通(简称苏通)GIL综合管廊工程是淮南-南京-上海1×106 V特高压交流输变电工程的重要组成部分，也是华东特高压交流环网合环运行的“咽喉要道”和控制性工程。工程起于南岸(苏州)引接站，止于北岸(南通)引接站，经由长达5.5 km的江底隧道穿越长江。管廊上层敷设两回1×106V GIL，单相长度达5.8 km，是世界上电压等级最高、输送容量最大，技术水平最高的超长距离GIL创新工程，下层预留两回5×105 V电缆以及通信、有线电视等市政通用管线[2]。

苏通GIL综合管廊工程是世界上首次在重要输电通道中应用特高压GIL技术，因此对其运行可靠性的要求极高。但是在制造、运输和现场组装等环节中都可能导致GIL内部产生绝缘缺陷，造成GIL带电调试或运行时发生电弧击穿故障。由于管廊内空间小，同时由于特高压GIL气室大、管道长，进一步增大了故障点排查和修复的难度。为了提高特高压GIL故障检修效率，保障其长期安全稳定运行，亟需开展特高压GIL电弧击穿故障定位技术研究。当GIL内部发生电弧击穿时，通常会在GIL筒体的击穿点上产生声源激励，进而形成声波在管廊内的传播。因此可将电弧击穿部位作为声源，采集管廊内的声波信号，然后采用适当的分析算法实现电弧故障点的准确定位。

综上所述，电弧击穿所产生的声波可作为对其进行定位的依据，因此，研究管廊的声传播特性可对GIL电弧击穿故障定位起到指导作用。对于管道内的声传播特性计算，常用的有解析方法和数值仿真方法。解析方法[3]通常适用于管道外形简单且内部截面规则的管道，这样可以推导出管廊内的声传播方程，进而快速地计算声场分布。数值仿真方法通常有边界元方法 (Boundary Element Method, BEM)[4-6]和有限元方法 (Finite Element Method, FEM)[7-8]。使用BEM首先需要推导出声场分布的基本函数，即格林函数，通常复杂模型对应较复杂的格林函数，因此增加了BEM的使用难度。FEM的优势在于其灵活性和适应性，但其网格量通常要多于其它方法。

苏通GIL综合管廊内包含两回GIL线路，每回GIL有三根管道，模型比较复杂。因此，本文采用FEM计算管廊内的声场分布，分析其声传播特性。

1 GIL综合管廊的物理模型和有限元模型

1.1 物理模型

苏通GIL综合管廊的纵断面如图1所示，管廊随江底地形高低起伏，长度约为5.5 km，GIL在两岸的接引站经过竖井后与地面的架空线相连。管廊的横断面布置情况如图2所示，两回特高压GIL布置在管廊上层，因为特高压GIL外壳尺寸较大，其对声波传播的影响不可忽略。GIL管道和管廊沿轴线平行布置，因此声波传播的管道截面是不变的，根据声波导管理论，管廊内存在一个截止频率。当GIL内部发生电弧击穿时，会在GIL筒体上产生声源，随后声波将通过管廊内的空气向周围传播。研究声波在管廊内的传播问题属于考虑了空气介质的声场求解和分析问题，对管廊内的声波传播特性分析应集中在低频段，因此在对管廊声场分布进行计算时，只需考虑在管廊内连续分布且几何尺寸较大的结构，即管廊壁和GIL筒体。管廊被分隔为上下两层，隔板地面提供硬壁反射边界，因此计算管廊的声场分布只需考虑上层部分。简化后的管廊模型由管廊壁、隔板地面和GIL筒体组成，其横断面如图3所示，管廊壁、隔板地面和不被内部力源激励的GIL筒体均提供硬壁反射边界。

图1 GIL综合管廊纵断面图

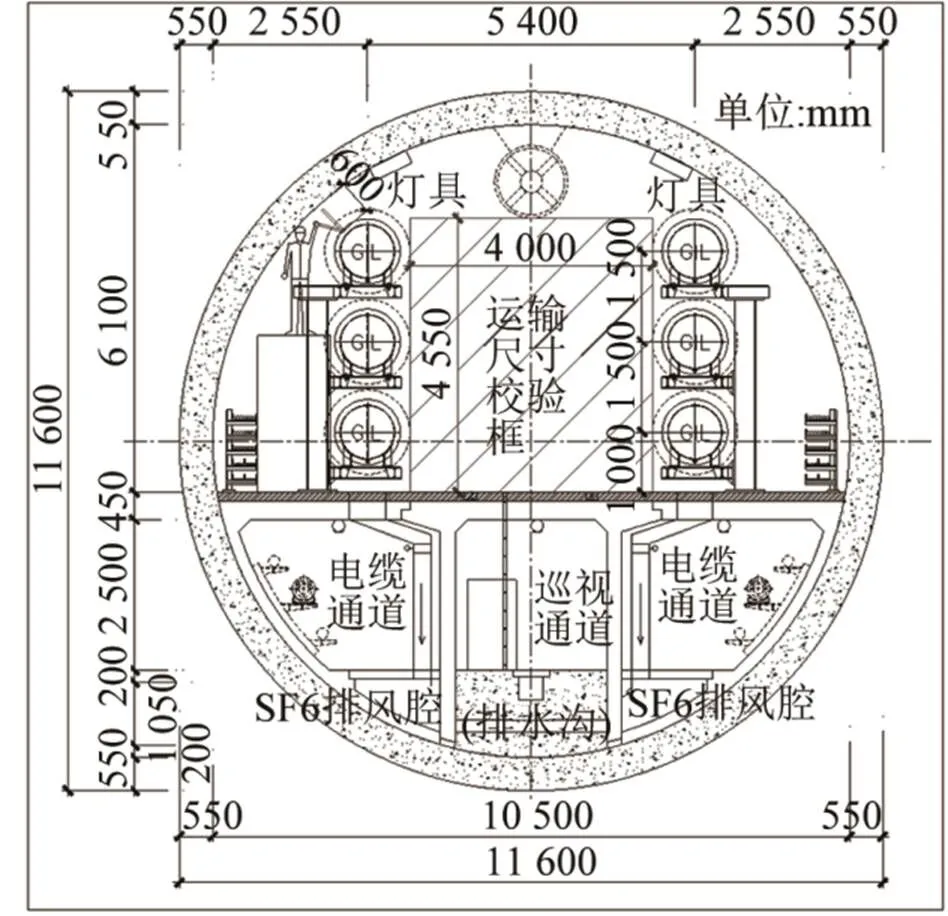
图2 GIL管廊横断面布置图

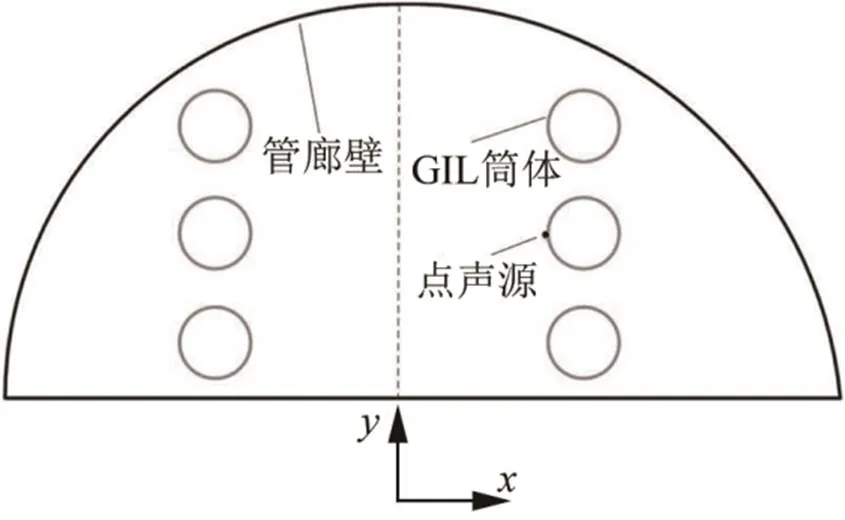
图3 计算管廊模型横断面示意图

1.2 有限元模型

由于管廊长达5.5 km，因此将有限元模型分为两种，一是远离接引站端面的模型，二是接引站端面附近的模型。第一种FEM计算模型如图4(a)所示，计算所用管廊长度设定为200 m，声源位置在100 m处，管廊两端均假设为无限远边界，两端设置为吸声匹配层(Perfectly Matched Layer, PML)来模拟无限远边界条件。第二种FEM计算模型如图4(b)所示，计算所用管廊总长以及声源位置同第一种计算模型，模型的一端是无限远边界条件，用PML吸声匹配层来模拟；另一端是管廊接引站端面，其相对于空气为硬壁边界。图中仅示出轴向坐标值，径向坐标参考图2中管廊的横断面尺寸。

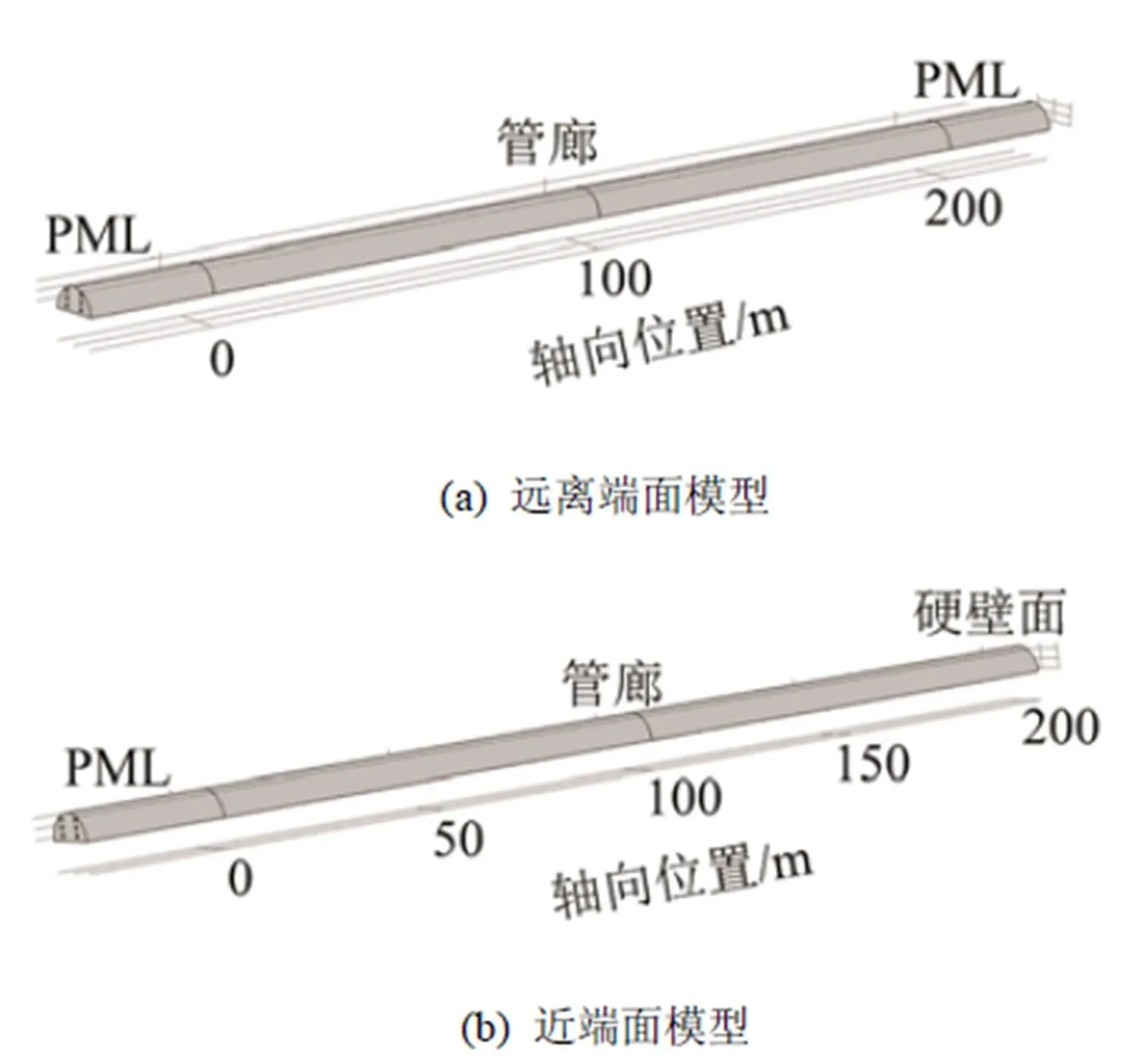
图4 管廊有限元计算模型

1.3 有限元方法基本理论

采用FEM求解模型的性能最后都归结于求解离散化的有限元方程，也即是有限元矩阵方程。这里需要求解的声学有限元方程为[8]

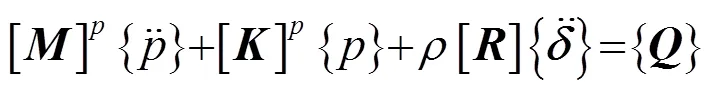
2 声场计算

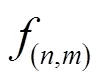
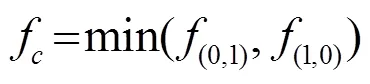
假设管廊内空气温度为20℃，空气密度=1.21 kg·m-3，空气介质中声传播速度为=343 m·s-1。计算模型中6路GIL的筒体半径均为1 m，将6路GIL筒体均设为硬壁边界，参照图2所示的尺寸设置6路GIL的空间位置以及管廊尺寸，建立如图4所示的两种FEM计算模型，并分别进行计算。

2.1 远离端面模型

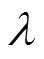
每一回GIL由三条线路组成，两回GIL在空间上是对称分布的，因此只需对其中一回GIL进行计算分析。

图5 计算模型有限元网格图沿xoy面投影

将点声源放置在中间GIL外壳的左端，对其产生的管廊声场分布特性进行研究。此处给出了点声源频率为1、15、16、20 Hz时的管廊内声压场幅值分布沿面的投影，分别如图6～9所示。

由图6～9可知，频率为1、15 Hz的点声源所引起的管廊内声场在远离点源位置为一维平面波场。虽然在点声源附近有非均匀的高次波存在，但它们在传播过程中迅速衰减，只剩下(0,0)次波传播。频率为16 Hz时，除了点声源附近有明显的高次波，在远离点声源的位置也有部分高次波存在，但高次波幅值不太大；点声源频率为20 Hz时，在整个管廊内有明显的高次波存在。

图6 由模型(a)计算的点声源频率为1 Hz时管廊内声场分布

图7 由模型(a)计算的点声源频率为15 Hz时管廊内声场分布

图8 由模型(a)计算的点声源频率为16 Hz时管廊内声场分布

图9 由模型(a)计算的点声源频率为20 Hz时管廊内声场分布

在管廊正中轴向切面与管廊顶部圆弧面的交界线上取点，画出管廊内声压幅值随轴向位置的分布曲线，鉴于对称性，这里只给出了100～200 m范围内的声压幅值曲线。点声源频率为1 Hz和15 Hz对应的曲线分别如图10和图11所示。由两图中的曲线可知，声场中的高次波在向远处传播时，首先经历一个衰减过程，频率越低，衰减越快，对应在管廊中形成一维平面波所需的时间也越短。

图10 频率为1 Hz的点声源对应管廊内声压幅值随轴向位置变化曲线

图11 频率为15 Hz的点声源对应管廊内声压幅值随轴向位置变化曲线

由于GIL各条线路所处的空间位置不同，它们单独发生故障时所产生的声场可能不同，因此需要对每条线路发生故障时产生的声场分别进行计算；另外，GIL筒体的直径较大，其影响因素不可忽略，本文对每个筒体的上、下、左、右等位置布放点声源时所产生的声场也进行了计算。结果表明，各条GIL线路及其位于各处的声源所产生的声场分布特性相似。因此，本文分析了位于管廊右侧中间的GIL线路筒体左端位置的声源产生的声场分布特性，其他情况不再赘述。

2.2 近端面模型

计算模型如图4(b)所示，计算所用的管廊长度取200 m，点声源布置在轴向位置100 m处，即GIL中部，如图3所示，从截面上看位于GIL筒体的左端，其振动幅值设置为1 N·m-1，管廊一端假设为无限远边界，将其设置为PML吸声匹配层来模拟无限远边界条件，另一端为硬壁反射边界。同样对多个典型位置的点声源产生的声场分布进行了计算和分析，发现了和远端面模型相似的声场分布规律，即点声源作用的近端面模型满足均匀截面的声波导管理论。因此，这里只给出了其中一个点声源位置的声场计算结果进行代表说明。

点声源位于右侧中间GIL筒体的左端。声源频率为1、15、16、20 Hz时的管廊内声压场幅值分布沿面的投影，分别如图12、图13、图14、图15所示。

由图12～15可知，频率为1、15Hz的点声源所引起的管廊内左半部分声场在远离点源位置为一维平面波场；虽然在点声源附近有非均匀的高次波存在，但它们在传播过程中迅速衰减，只剩下(0,0)次波传播。由于右端面是硬壁反射面，声场在声源的右半部分远离声源区域形成标准的驻波场，平面驻波场的声压幅值沿轴向是变化的。频率为16 Hz时，除了点源附近有明显的高次波，在远离点源的位置也有高次波的存在，但高次波的幅值不大；点声源频率为20 Hz时，整个管廊内有明显的高次波存在。

图12 由模型(b)计算的点声源频率为1 Hz时管廊内声场分布

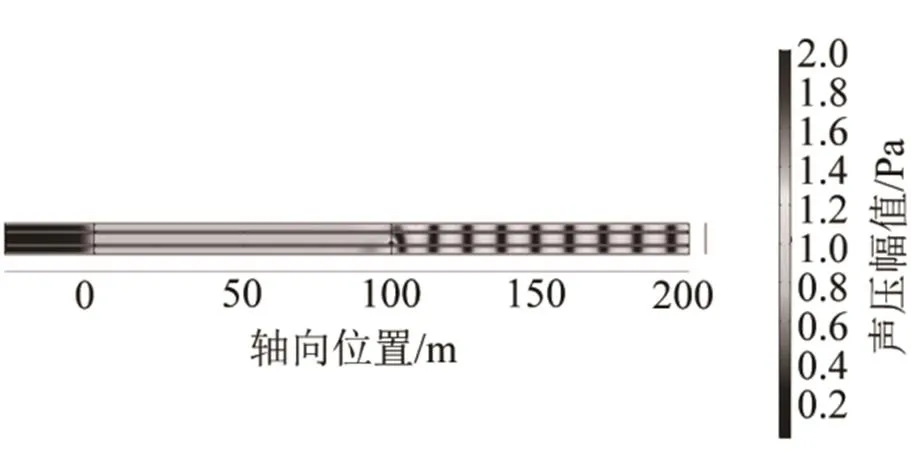
图13 由模型(b)计算的点声源频率为15 Hz时管廊内声场分布

图14 由模型(b)计算的点声源频率为16 Hz时管廊内声场分布

图15 由模型(b)计算的点声源频率为20 Hz时管廊内声场分布

点声源对应的平面驻波场中，相邻波节或波腹之间的距离是一致的，仍满足为声波波长的1/2。以15 Hz为例，因第一个波节与声源距离太近，波形受到影响，因此用其它波节计算。图13中驻波第二个波节的位置为120.7 m，第三个波节的位置为132.1 m，两波节之间的间距为11.4 m。

3 结语

GIL内部发生电弧击穿故障时，会在GIL筒体的击穿点位置产生强烈的瞬态冲击噪声，因此可根据其在管廊内的传播特性开展故障定位技术研究。本文从重大工程技术需求出发，根据管廊结构特点，提出了两种简化的计算模型，采用FEM对各条GIL线路及不同位置点声源所产生的声场分布进行了计算和分析。结果表明，管廊中GIL线路以及点声源的位置对于声波传播特性的影响不大；对于非均匀声源，苏通GIL综合管廊的平面波截止频率在15 Hz附近。如果声源频率低于15 Hz，高阶模态声波快速衰减消失，声波在传播过程中会快速转化为一维平面波，可直接采用时延(Time Delay of Arrival, TDOA)算法基于直达声传播路径进行声源定位；如果声源频率高于15 Hz，冲击噪声由声源点经过多次壁面反射后到达接收点，声传播路径增加，且不同频率分量的声波具有不同的传播途径，采用TDOA算法无法直接进行声源定位，需对采集到的声波信号做进一步的时域和频域分析，分析管廊中不同频率声波的传播特性，根据响应时间计算声波在管廊中的传递函数，从而确定声源信号在管廊中的传播途径。根据声源传播途径修正定位算法，从而实现声源准确定位。

通过对苏通GIL综合管廊声波传播特性的仿真研究，初步掌握了管廊内的声波传播规律，为电弧故障定位技术提供了理论依据和工作方向，为下一步开展基于声波传播特性的GIL电弧击穿故障定位技术可行性论证和后续方案设计具有重要的指导意义。

[1] 李鹏, 颜湘莲, 王浩, 等. 特高压交流GIL输电技术研究及应用[J]. 电网技术, 2017, 41(10): 3161-3167.

LI Peng, YAN Xianglian, WANG hao, et al. Research and application of UHVAC gas-insulated transmission line[J]. Power System Technology, 2017, 41(10): 3161-3167.

[2] 佚名. 特高压苏通GIL综合管廊工程[J]. 电力工程技术, 2017, 36(1): 2.

ANON. Suzhou-Nantong UHV GIL multi-utility tunnel project[J]. Electric Power Engineering Technology, 2017, 36(1): 2.

[3] 管莹, 王同庆, 王利. 流管实验装置中声传播计算的模态方法[J]. 工程热物理学报, 2006, 27(4): 595-597.

GUAN Ying, WANG Tongqing, WANG Li. A mode matching method for calculating sound propagation in flow duct equipment[J]. Journal of Engineering Thermophysics, 2006, 27(4): 595-597.

[4] MYERS M K. Boundary integral formulations for ducted faradization calculations[J]. CEAS/AIAA Paper, 1995, 14: 69-76.

[5] 袁亮, 倪樵, 刘攀, 等. 用有限元/边界元方法计算U型管振动声辐射[J]. 华中科技大学学报, 2006, 23(1): 39-42.

YUAN Liang, NI Qiao, LIU pan, et al. Calculation of vibration acoustic radiation of U tube by finite element method/boundary element method[J]. Journal of Huazhong University of Science and Technology, 2006, 23(1): 39-42.

[6] 王同庆, 张莉爽, 杨兵, 等. 变截面风扇管道快速声散射计算[J]. 航空动力学报, 2011, 26(7): 1569-1574.

WANG Tongqing, ZHANG Lishuang, YANG bing, el al. Aeroacoustic scattering via the fast scattering method[J]. Journal of Aerospace Power, 2011, 26(7): 1569-1574.

[7] 张乃龙, 杨文通, 费仁元. 基于ANSYS的抗性消声器性能仿真分析[J]. 计算机仿真, 2006, 23(8): 306-310.

ZHANG Nailong, YANG Wentong, FEI Renyuan. Simulation and analysis of reactive muffler based on ANSYS software[J]. Computer Simulation, 2006, 23(8): 306-310.

[8] 郭金泉, 杨晓翔. 管道振动引起辐射噪声场的有限元分析[J]. 力学与实践, 2006, 28(1): 36-40.

GUO Jinquan, YANG Xiaoxiang. Finite element analysis of radiated noise field in pipes vibration[J]. Mechanics in Engineering, 2006, 28(1): 36-40.

[9] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2012.

DU Gonghuan, ZHU Zhemin, GONG Xiufen. Acoustic foundation[M]. Nanjing: Nanjing University Press, 2012.

Simulation study of acoustic propagation characteristics in Suzhou-Nantong GIL multi-utility tunnel

LI Yong-liang1, TANG Jun2, DANG Dong1, YAN Ye1, LIU Zhi-fang1

(1.China Electric Power Research Institute, Beijing 100192, China; 2. Suzhou Sound-Tech Environment Technology Co., Ltd, Suzhou 215638,Jiangsu,China)

The Suzhou-Nantong GIL multi-utility tunnel is an innovative engineering project using super long distance GIL with so far the highest voltage level, the largest transmission capacity and the highest technological level in the world. By analyzing the internal structure of the multi-utility tunnel, the physical model of the multi-utility tunnel is built, and two calculating models are put forward based on the acoustic theory and the layout mode of the multi-utility tunnel. The finite element method is applied to calculating the sound field distribution of the multi-utility tunnel, and it can provide a reference for locating the fault position in the tunnel. The results show that for nonuniform sound source, the cut-off frequency of the plane wave in the multi-utility tunnel is around 15 Hz. If the frequency of sound source is below 15 Hz, the sound wave can be rapidly transformed into plane wave during its propagation. Therefore, the fault position can be simply located by TODA (Time Difference of Arrival) method. If the frequency of sound source is higher than 15 Hz, the sound signal should be further analyzed in time domain and frequency domain to determine the appropriate location algorithm.

Suzhou-Nantong GIL multi-utility tunnel; Gas-Insulated metal-enclosed transmission Line (GIL); electric breakdown; fault location; finite element analysis

O241.82 O422.1

A

1000-3630(2018)-04-0297-06

10.16300/j.cnki.1000-3630.2018.04.001

2018-02-26;

2018-04-15

李永亮(1982－), 男, 山西大同人, 硕士, 高级工程师, 研究方向为高电压技术、输变电设备运维检修技术。

李永亮,E-mail: lily82@epri.sgcc.com.cn