关于I2上的max-drast矩阵的特征空间

陈伟

(闽南师范大学数学与统计学院,福建 漳州 363000)

1 引言

模糊矩阵的特征向量对应于一个复杂的离散事件系统的稳定状态,由给定的矩阵和模糊状态向量决定.因此,寻找所有可能的稳定状态就相当于描述矩阵A的所有特征向量.这个问题已经在一些模糊代数中得到解决,例如max-plus代数,min-plus代数,max-prod代数和max-min代数,详见参考文献[1-9].

Imran Rashid等学者在文献[1]中研究了I=[0,1]上的max-drast代数模糊矩阵的特征空间.他们给出在I上对于一个给定的矩阵它的递增特征向量非空的充分必要条件,描述了I上的递增特征空间的结构.

本文主要把文献[1]的主要结果推广到I2=[0,1]×[0,1],定义了带有两个二元运算的代数 (I2,⊕,⊗),其中 ⊕=max,⊗=drast,研究了在I2上的矩阵的特征空间,刻画了对于阶数一定的矩阵的特征空间的组成结构,还得到了对于给定的矩阵的严格递增的特征空间存在的充分必要条件.

本文用I2[n,n](I2[n])来表示定义在I2上的所有给定阶数n×n(n×1)的方阵(向量)的集合.⊕,⊗是通过形式化的方法类似地扩展到矩阵和向量的运算.max-drast代数中一个给定矩阵A∈I2[n,n]的特征问题在于找到一个特征向量X∈I2[n]使得A⊗X=X,其中

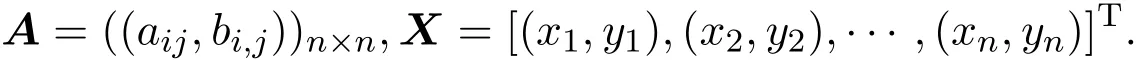
可以把X 简单记为[x,y],一个矩阵A∈I2[n,n]的特征空间记为:

2 max-drast代数的特征空间

本文接下来定义在I2上的偏序关系≤,max加法运算⊕和drast乘法运算⊗:对任意 (xi,yi),(xj,yj)∈I2,有:

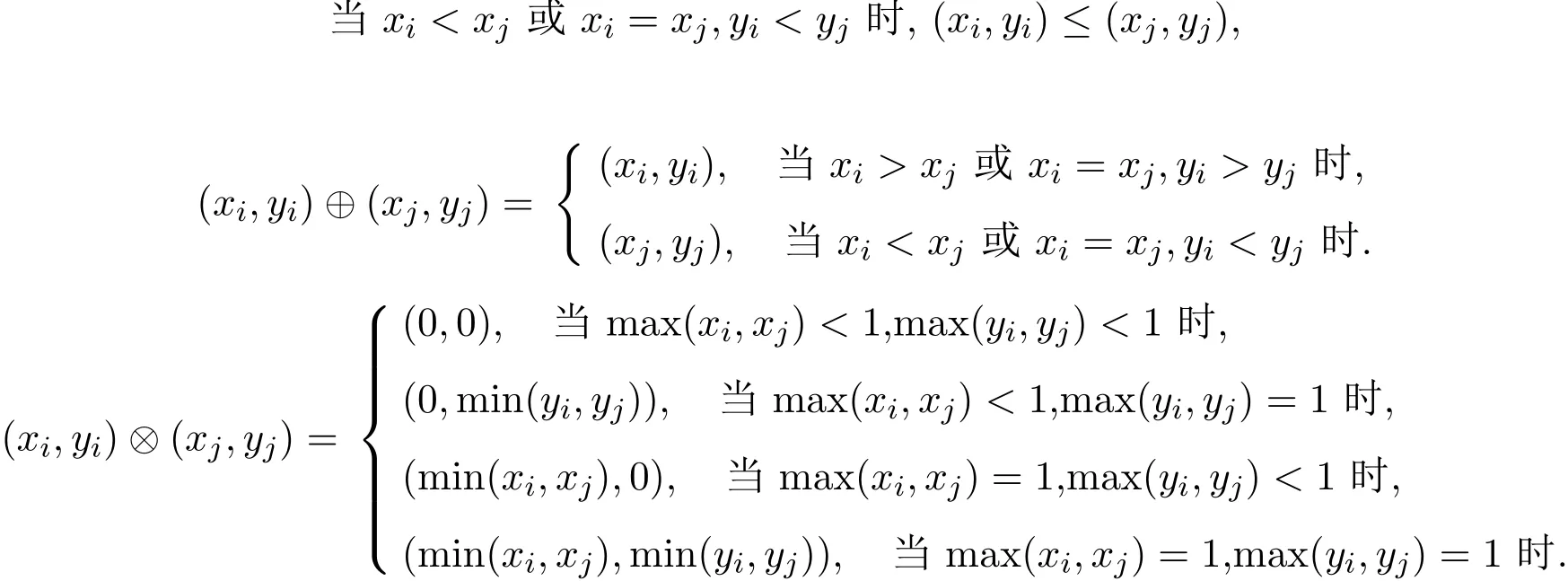
用F<(A)表示矩阵的严格递增的特征空间.其中

类似地,可以给出I2<[n]的定义.

下面给出在 I2上的 max-drast矩阵的特征空间及特征向量的刻画,这些结果推广了文献 [1]中的命题3.1-命题3.3.

命题 2.1 令A∈I2[n,n],[x,y]∈I2[n].则[x,y]∈F(A)充分必要条件是∀i∈N满足下面两个条件:

命题 2.2 令A∈I2[n,n],[x,y]∈I2<[n].则[x,y]∈F<(A)充分必要条件是∀i∈N满足下面两个条件:

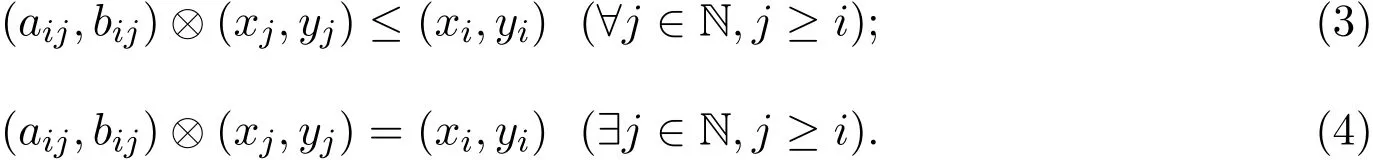
证明 因为[x,y]∈I2<[n],所以可知[x,y]是严格单调递增的.又因为

于是

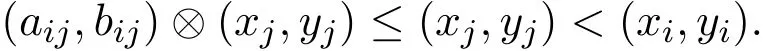
因此由命题2.1可得此结论.

命题 2.3 令A∈I2[n,n],[x,y]∈I2<[n].则[x,y]∈F<(A)充分必要条件是∀i∈N满足下面三个条件:

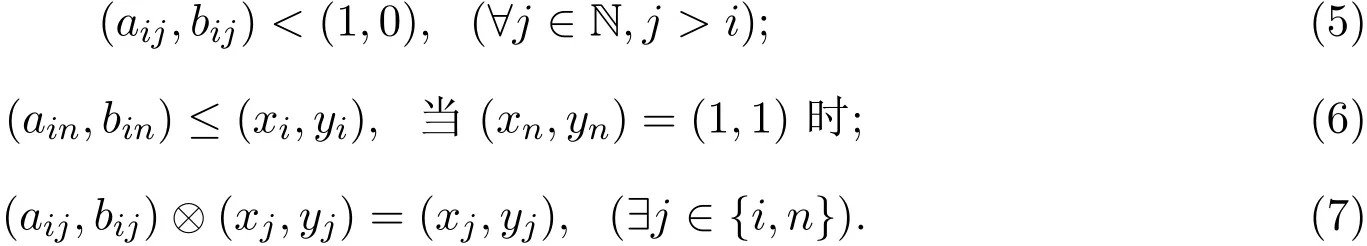
证明 设 [x,y]∈F<(A).假设 ∃j>i使得 (aij,bij)=(1,bij),那么

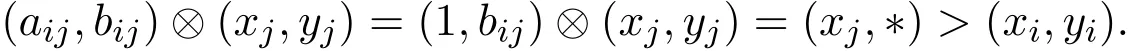
这与条件(3)矛盾.所以,条件 (5)成立.假设(xn,yn)=(1,1)时,有 (ain,bin)>(xi,yi).那么 (ain,bin)⊗(xn,yn)=(ain,bin)⊗(1,1)=(ain,bin)>(xi,yi),这与条件(3)矛盾.因此,条件(6)成立.由条件(5)可知对于每个j∈N,i

下面给出一个方阵有严格递增的特征向量的充要条件.

定理 2.1 令A∈I2[n,n].则F<(A)̸=∅充分必要条件是满足下面的条件:

(i)∀i,j∈ N,当i

(ii)∀i∈ N{1},且(aii,bii)<(1,1)时,(ain,bin)>(0,0);

(iii)∀i,k ∈ N,k

(iv)(ann,bnn)=(1,1).

证明 首先,证明必要性.设 F<(A)̸=∅.则存在 [x,y]∈F<(A).于是对每个 i∈N,条件(3)-条件(7)都成立.

①事实上,条件(i)与条件(5)是等价的.

② 设 i∈N{1}且 (aii,bii)<(1,1).则 (aii,bii)⊗(xi,yi)<(xi,yi).其次,由条件 (7)可以得到 (ain,bin)⊗(xn,yn)=(xi,yi).但当 (ain,bin)=(0,0)时,这个结论就不成立,所以(ain,bin)>(0,0).即条件(ii)成立.

③ 设i,k∈N,k

所以(xn,yn)=(1,1).由条件(3)可得

又因为xk

由条件(7)可知:

必成立,但(ann,bnn)<(1,1)时,(ann,bnn)⊗(xn,yn)=(xn,yn)不成立.所以

即条件(iv)成立。

接下来证明命题的充分性.设矩阵满足条件(i)-条件(iv).通过循环使用以下规则1-规则3,可得到递增的向量[x,y]∈I2[n].

规则1:若i

规则2:若i

(a)xi−1

(b)(ain,bin)≤(xi,yi)<(1,1);

(c)∀k∈N,k>i,(akk,bkk)<(1,1)有 (xi,yi)<(akn,bkn)(不适用于对任意的 k>i时都有(akk,bkk)=(1,1)).

规则3:对i=n,选择的(xn,yn)∈I2要满足:

(a)xn−1

(b)若(a11,b11)<(1,1),(0,0)<(a1n,b1n),则(xn,yn)=(1,1);

(c)若 ∃k∈N,k>1使得 (akk,bkk)<(1,1),则 (xn,yn)=(1,1).

根据上述的规则,可以得到满足条件的[x,y]∈I2[n].

由条件 (i)得到的准确的 [x,y]∈I2[n],可以验证条件 (7)是正确的.因此,可以证明条件(i)-条件(iv)也是充分的.

下面给出一个给定的max-drast矩阵特征空间的结构.从而推广了文献[1]中的定理3.5.

定理 2.2 设 A∈I2[n,n]满足定理 2.1中的条件 (i)-条件 (iv).令 [x,y]∈I2<[n].则[x,y]∈F<(A)充分必要条件是满足以下条件:

(v)∀i∈ N,且(aii,bii)<(1,1)时,(xi,yi)=(ain,bin);

(vi)若(xn,yn)=(1,1),则∀i∈N{n},且(aii,bii)=(1,1)时,(xi,yi)≥ (ain,bin);

(vii)若(a11,b11)<(1,1),(0,0)<(a1n,b1n),则(xn,yn)=(1,1);

(viii)若∃i∈ N{1}使得 (aii,bii)<(1,1),则(xn,yn)=(1,1).

证明 由命题2.3和定理2.1的证明中容易得到.