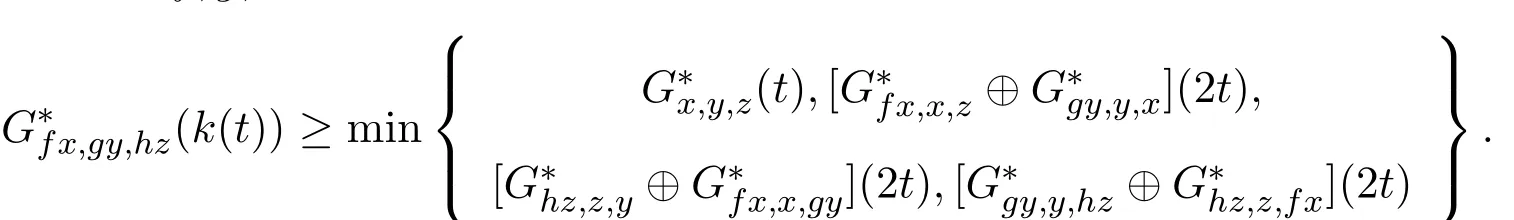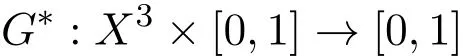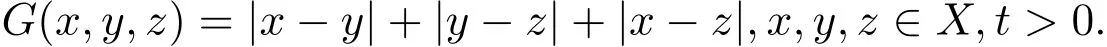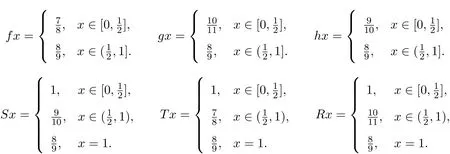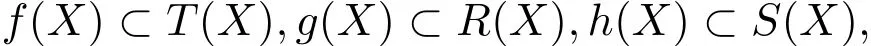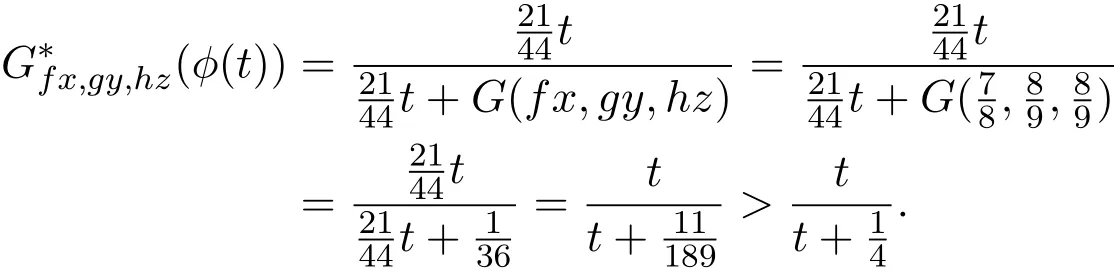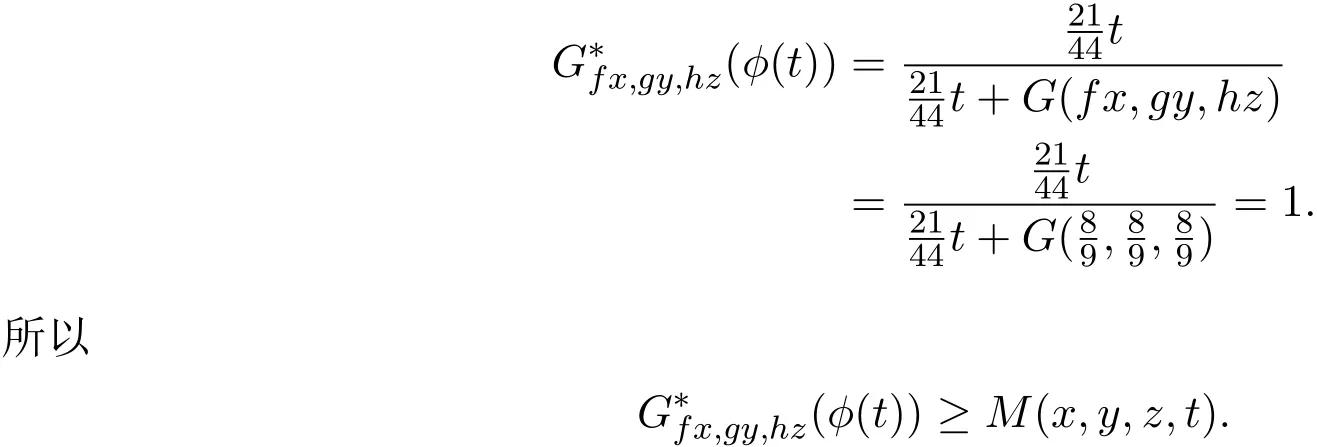Menger PGM-空间中弱相容映射对的公共不动点定理
张倩雯,谷峰
(杭州师范大学数学系,浙江 杭州 310036)
1 引言
1960年,文献 [1-2]使用 t-范数,引进了 Menger概率度量空间的概念(简称为Menger PM-空间),并讨论了该空间的一些基本性质.1994年,文献[3]对Menger PM-空间的一些重要成果进行了总结.2006年,文献[4]提出了G-度量空间的概念,它是度量空间的一个推广.2014年,文献 [5]在 G-度量空间和 Menger PM-空间的基础上,引入了 Menger概率 G-度量空间(简称为Menger PGM-空间)的概念.之后,文献[6-7]在 Menger PGM-空间中引入了ϕ-压缩条件和映射对弱相容的概念,证明了几个公共不动点定理.
2016年,文献[8]在G-度量空间中证明了几个弱相容映射对的公共不动点定理.本文受其启发,在Menger PGM-空间中证明了弱相容映射对的几个新的公共不动点定理,并给出了一个用以说明新结果有效性的实际例子.本文的结果完全不同于已有文献中的结果.
在介绍主要结果之前,先给出Menger PGM-空间的一些相关概念.
设R表示一切实数的集合,R+表示一切非负实数的集合,Z+表示所有正整数的集合,N表示所有自然数的集合.
定义 1.1[3]称映射F:R→ R+为分布函数,如果它是单调不减的、左连续的,且满足 inft∈RF(t)=0,supt∈RF(t)=1.
用D表示一切分布函数的集合,D+={F∈D:F(t)=0,∀t≤0},H(t)表示一特殊的分布函数,其定义如下:

定义 1.2[1]若映射∆:[0,1]×[0,1]→[0,1],且∀a,b,c,d∈[0,1],有下列条件被满足:
(∆-1)∆(a,1)=a;
(∆-2)∆(a,b)=∆(b,a);
(∆-3)a≥b,c≥d⇒∆(a,c)≥∆(b,d);
(∆-4)∆(a,∆(b,c))= ∆(∆(a,b),c).
则称∆为三角范数(简称为t-范数).
三个典型的连续t-范数是:
∆1(a,b)=min{a+b−1,0},∆2(a,b)=ab,∆m(a,b)=min{a,b},其中 a,b∈[0,1].
定义 1.3[3]Menger PM-空间是一个三元组(X,F,∆),其中X 是一个非空集合,∆是一个连续的t-范数,F:X×X→D是满足下面条件的映射:
(PM-1)Fx,y(t)=H(t)当且仅当x=y,t=0;
(PM-2)Fx,y=Fy,x对任意的x,y∈X;
(PM-3)Fx,y(t+s)≥∆(Fx,z(t),Fz,y(s))对任意的x,y,z∈X,s,t≥0都成立.
其中Fx,y表示F在点(x,y)处的值.
定义 1.4[4]设X是一个非空集合,G:X×X×X→R+为一函数,且满足以下条件:
(1)G(x,y,z)=0⇔x=y=z;
(2)G(x,x,y)>0,∀x,y∈ X 且 x ̸=y;
(3)G(x,x,y)≤ G(x,y,z),∀x,y,z∈ X 且 z̸=y;
(4)G(x,y,z)=G(x,z,y)=G(y,z,x)= ···,∀x,y,z ∈ X;
(5)G(x,y,z)≤ G(x,a,a)+G(a,y,z),∀x,y,z,a∈ X.
则称函数G是X 上的一个广义度量,简称为X上的一个G-度量,并称(X,G)是一个广义度量空间,简称为G-度量空间.
定义1.5[5]Menger概率G-度量空间(简称Menger PGM-空间)是一个三元组(X,G∗,∆),其中X是非空集合,∆是连续的t-范数,G∗:X×X×X→D是满足下列条件的映射:
(PGM-2) ∀x,y,z ∈ X,z ̸=y,t>0,
(PGM-4) ∀x,y,z,a ∈ X,s,t≥ 0,
例 1.1[5]设 X=R,G(x,y,z)=|x−y|+|y−z|+|x−z|,∀x,y,z∈X.则(X,G)是一个G-度量空间.令

则 (X,G∗,∆m)是一个 Menger PGM-空间.
定义 1.6[5]设 (X,G∗,∆)是一个 Menger PGM-空间,x0∈X.∀ε>0,0< δ<1,定义 x0的 (ε,δ)-邻域如下:
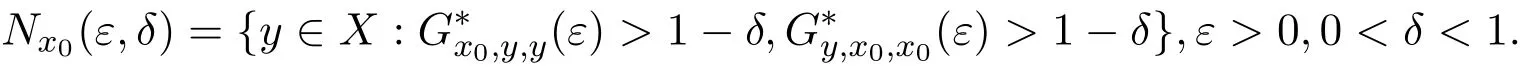
这意味着Nx0(ε,δ)是X 中满足x0到 y的距离小于ε的概率大于1−δ的所有 y的集合.
定义 1.7[5]设(X,G∗,∆)是一个Menger PGM-空间,{xn}是X 中的序列,x∈X.
(1) 若对任意的 ε>0,0< δ<1,存在正整数 Mε,δ,使得当 n>Mε,δ时,xn∈ Nx(ε,δ),则称{xn}收敛于点x,记为=x或者xn→x(n→∞).
(2)若对任意的 ε>0,0<δ<1,存在正整数 Mε,δ,使得当 n,m,l>Mε,δ时,

则称{xn}是X中的一个柯西列.
(3)若X 中所有的柯西点列都收敛于X 中的某点,则称(X,G∗,∆)是完备的.
引理 1.1[6]设(X,G∗,∆)是一个Menger PGM-空间,{xn}是X 中的序列.则以下叙述等价:
(1){xn}收敛于x∈X;
引理 1.2[6]设 (X,G∗,∆)是一个具有连续t-范数∆的Menger PGM-空间,{xn},{yn}和{zn}是X 中的三个序列,x,y,x∈X.如果xn→x,yn→y,zn→z(n→∞),则有

特别的,如果t0是函数Gx,y,z(·)的连续点,则
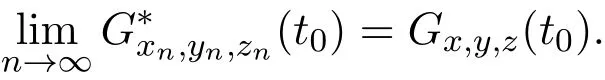
定义 1.8[9]∆ 称为是一个 H-型 t-范数,若函数族在 t=1处是等度连续的,即对任意 ε∈(0,1),存在 δ∈(0,1),使得 t>1−δ⇒ ∆n(t)>1−ε,n∈Z+.其中 ∆1(t)= ∆(t,t),∆m(t)= ∆(t,∆m−1(t)),m=2,3,···,t∈ [0,1].
引理 1.3[10]设 (X,G∗,∆)是一个 Menger PGM-空间.对任意 λ∈(0,1],定义函数如下:

则以下结论成立:

定义 1.9[13]设ϕ:R+→R+,满足下述条件:
(1)ϕ是非减的;
(2)ϕ是右上半连续的;

记Φ为所有满足上述条件(1)-条件(3)的函数ϕ的集合.
定义 1.10[12]设F1,F2∈D,F1和F2的代数和F1⊕F2定义为:
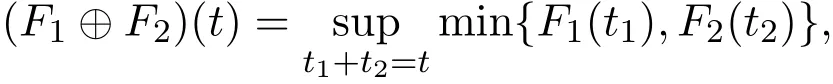
其中t∈R.
定义 1.11[6]设S和T是Menger PGM-空间(X,G∗,∆)中的自映射.S和T称为是弱相容的,如果S和T在重合点处是可交换的,即{u∈X:Tu=Su}⊂{u∈X:TSu=STu}.
引理 1.4[6]设(X,G∗,∆)是一个Menger PGM-空间,x,y,z∈X.如果存在ϕ∈Φ,使得

则x=y=z.
引理 1.5[13]设 (X,G∗,∆m)是一个 Menger PGM-空间,x,y,z∈X.如果存在 ϕ∈Φ,使得
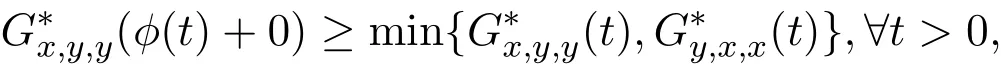
则x=y.
引理 1.6[10]设(X,G∗,∆)是一个Menger PGM空间,∆是连续的t-范数,则下面两个叙述等价:
(1)序列{xn}是柯西列;
(2)对任意ε>0,0<λ<1,存在M ∈Z+使得(ε)>1 − λ,n,m>M.
2 主要结果
引理 2.1 设 (X,G∗,∆)是一个 Menger PGM-空间,{G∗λ}λ∈(0,1]是由 (1)式所定义的 X上的函数族.如果∆是H-型t-范数,则对任意λ∈(0,1],存在µ∈(0,λ],使对任意m∈Z+,x0,x1,···,xm∈ X,有

证明 由 ∆ 是 H-型 t-范数,故对任意 m∈Z+,x0,x1,···,xm∈X,存在 µ∈(0,λ],使得

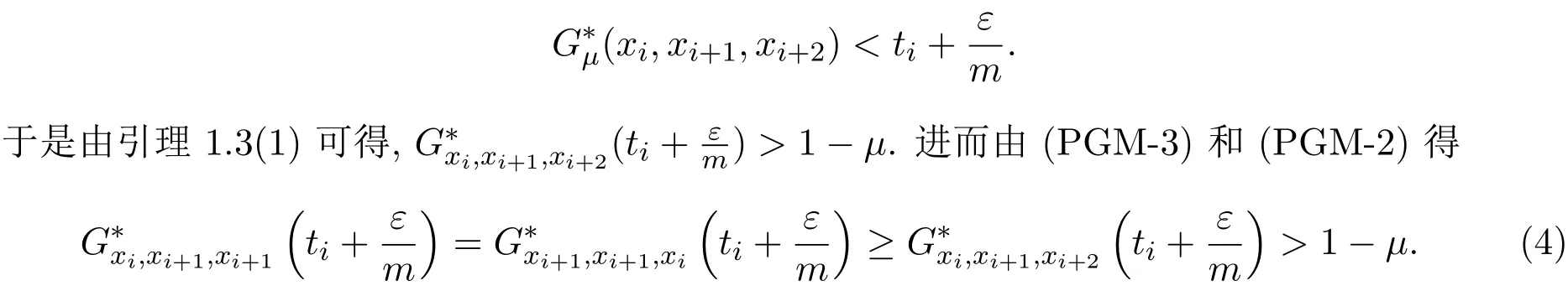
使用(3)式-(4)式和(PGM-4)可得


引理 2.2 设 (X,G∗,∆)是一个 Menger PGM-空间,其中 ∆ 是连续的 H-型 t-范数,{yn}⊂X.若存在函数ϕ∈Φ,使得
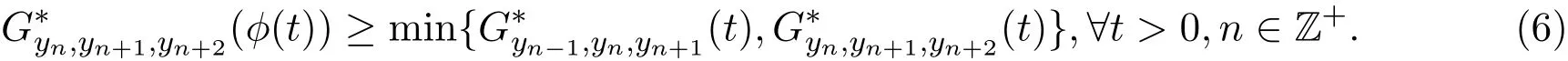
则{yn}是X中的柯西列.
证明 设 {G∗λ}λ∈(0,1]是引理 1.3中所定义的函数族,对任意 λ∈(0,1],n∈Z+,令

下面证明:

由于ϕ是右上半连续的,所以对∀ε>0和每个an,存在pn>an,使得ϕ(pn)<ϕ(an)+ε.由引理 1.3(1) 和.因此,由(6)式可得

于是,由引理1.3(1)可得
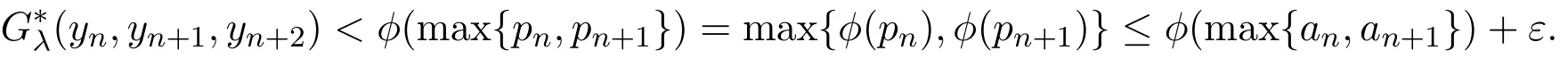
再由ε的任意性,可知

(7)式得证.
重复使用(7)式,对任意n∈Z+,有

由 ∆ 是H-型t-范数和引理 2.1可知,对任意λ∈(0,1],存在µ∈(0,λ],使得
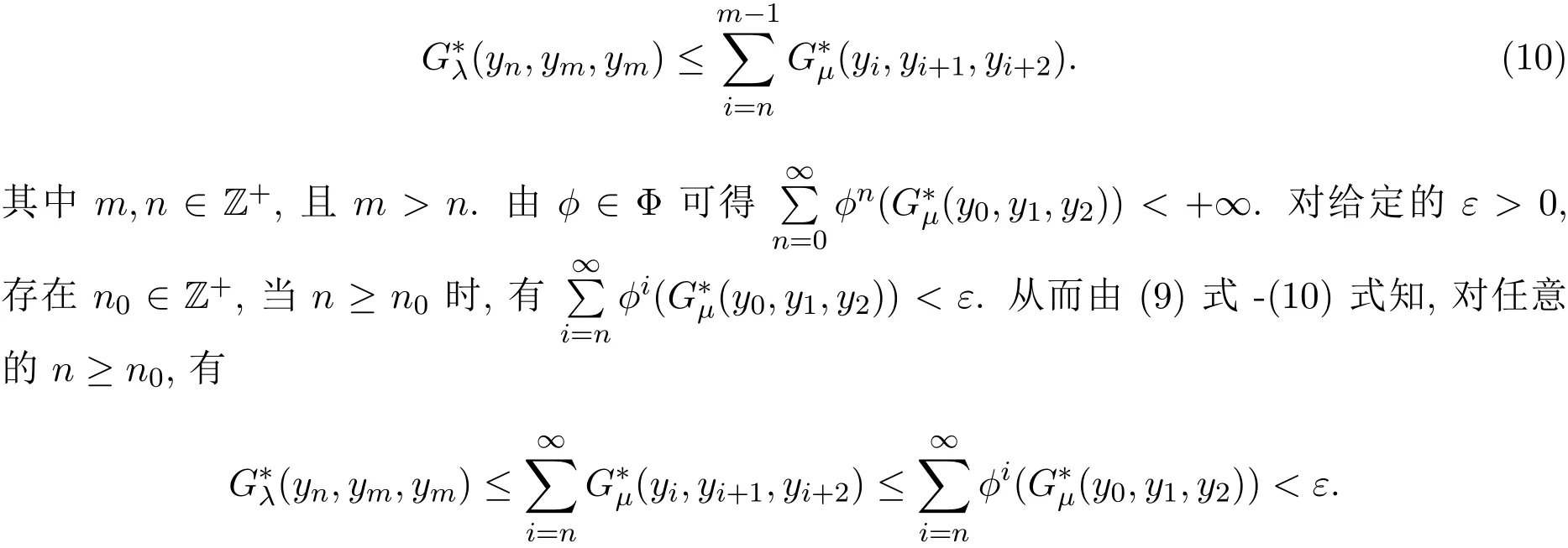
所以,由上式知,对任意m,n∈Z+,m>n≥n0,有(ε)>1− λ. 再由引理 1.6可知{yn}是X中的柯西列.
定理 2.1 设(X,G∗,∆m)是一个Menger PGM-空间,其中∆是连续的H-型t-范数,假设映射f,g,h,R,S,T:X→X满足下列条件:

∀x,y,z∈X,t>0,其中ϕ∈Φ.如果下列条件被满足:
(i)f(X)⊂T(X),g(X)⊂R(X),h(X)⊂S(X);
(ii)S(X),T(X)和R(X)是X的完备子空间.
则映射对(f,S),(g,T)和(h,R)在X 中有公共重合点.进一步,若映射对(f,S),(g,T)和(h,R)是弱相容的,则f,g,h,R,S和T在X中有唯一公共不动点.
证明 任取x0∈X,由条件(i)知,存在x1,x2,x3∈X,使得

反复使用(i),可得X 中的序列{xn}和{yn},使得
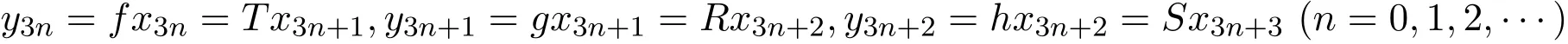
若 y3n=y3n+1,则有 gx=Tx,其中 x=x3n+1.若 y3n+1=y3n+2,则有 hx=Rx,其中 x=x3n+2.若 y3n+2=y3n+3,则有 fx=Sx,其中 x=x3n+3.因此,不失一般性,可令 yn̸=yn+1,∀n ∈ N.
接下来证明{yn}是X 中的柯西列.事实上,由(11)式可得

同理可证

组合(12)式 -(13)式和(4)式,可得

再由引理2.2可得{yn}是X中的柯西列.
下面证 (f,S)有重合点.不妨设 S(X)是 X的完备子空间.因为 {yn}是 X中的柯西列,则存在 p∈X,使得 yn→ p,进而 y3n→ p,y3n+1→ p,y3n+2→ p(n→ ∞).由 y3n+2=Sx3n+3→p,所以存在t∈X,使得p=St.由 (11)式得

令n→∞,则可得

则由引理1.4可知St=ft=p.
下证(f,S)有不动点.因为St=ft=p且(f,S)是弱相容的,所以有fp=Sp.由(11)式可得
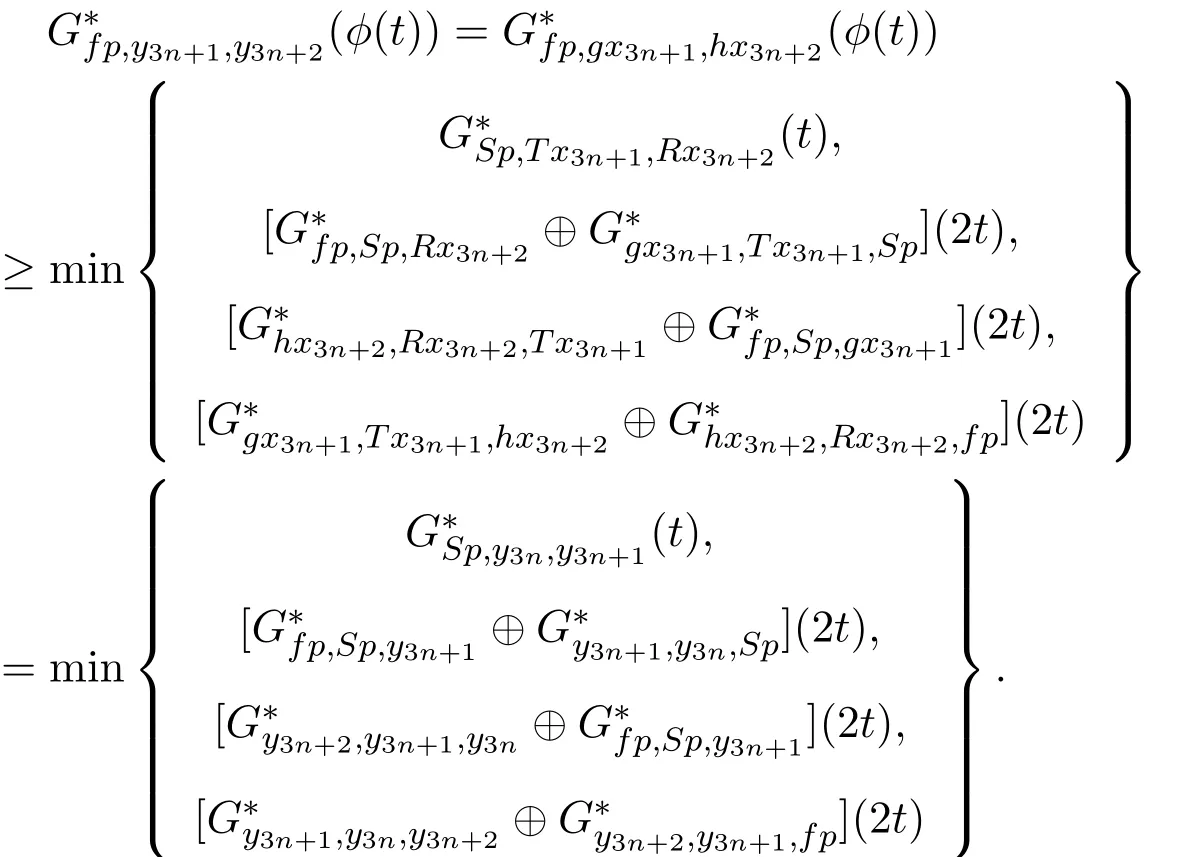
下证 (g,T)有重合像.因为 f(X)⊂T(X)和 p=fp⊂f(X),所以存在 v∈X,使得 p=fp=Tv.由(11)式可得

下证(g,T)有不动点.因为gv=Tv=p且(g,T)是弱相容的,所以有gp=Tp.由(11)式可得
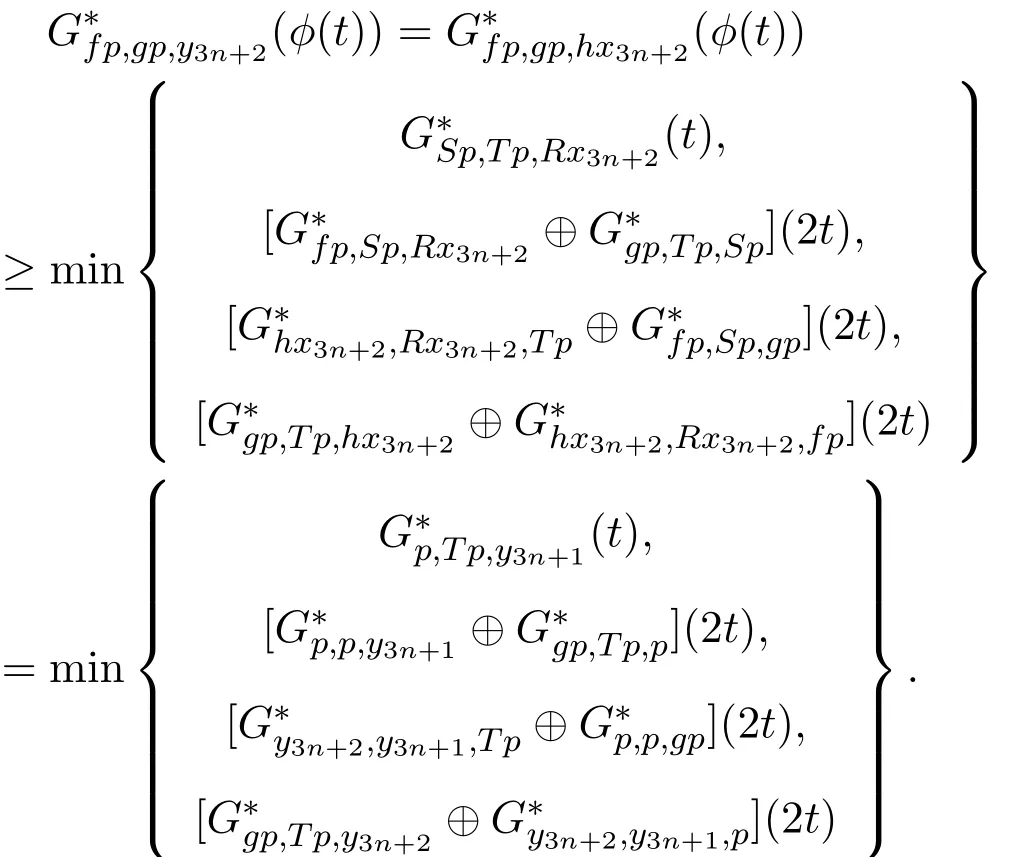
令n→∞,则可得到

则由引理1.5可知p=gp,因此gp=Tp=p,即p是(g,T)的不动点.
同理可得:hp=Rp=p.因此有fp=Sp=Tp=gp=hp=Rp=p.即f,g,h,S,T和R有公共不动点p.
下证唯一性.假设q是f,g,h,S,T和R的另一个公共不动点.由(11)式可得
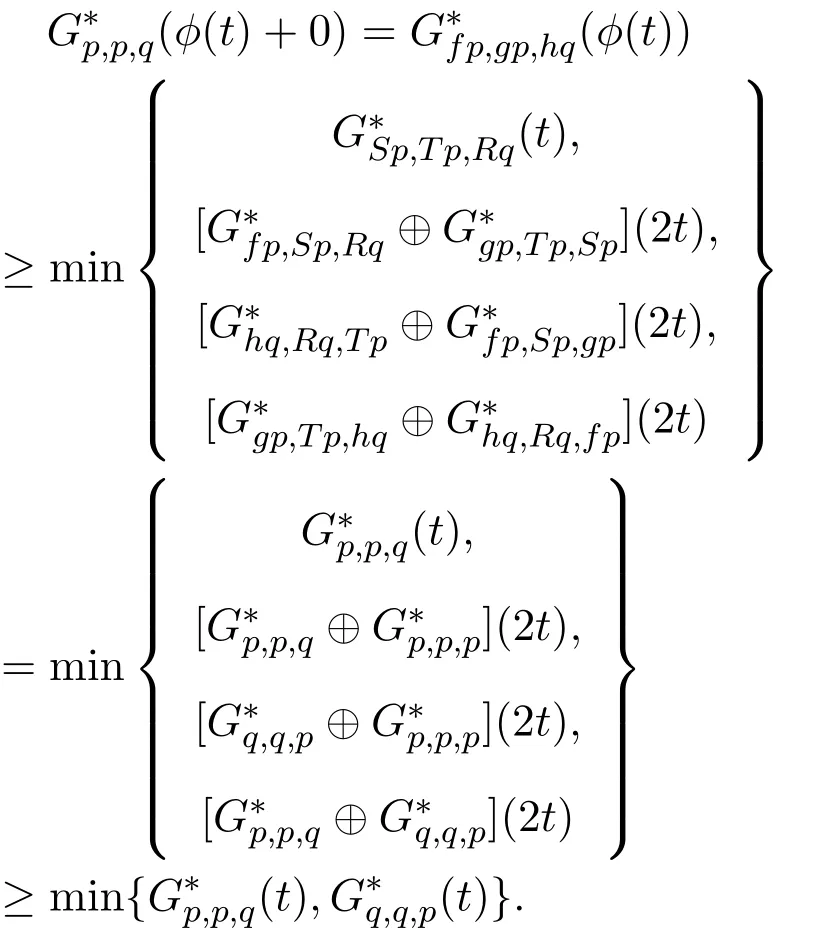
则由引理1.5可知p=q,因此p是f,g,h,S,T和R的唯一的公共不动点.
若T(X)或R(X)是X 完备子空间,证明过程相似.
例 2.1 设 X=[0,1],定义函数 G∗:X3×[0,1]→[0,1]为

其中 G(x,y,z)=|x−y|+|y−z|+|x−z|,x,y,z∈X,t>0.容易证得 (X,G∗,∆m)是一个 Menger PGM-空间,令 ϕ(t)=t,ϕ∈Φ,又定义f,g,h,S,T和R:X →X 如下:

容易得到f,g,h,S,T和R在X中不是G-连续的,f(X)⊂T(X),g(X)⊂R(X),h(X)⊂S(X),
S(X),T(X)和R(X)都是X的完备子空间.
下面证明映射f,g,h,S,T和R满足定理2.1中的(11)式,设





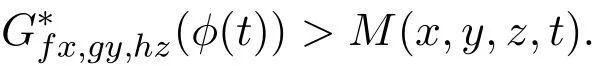

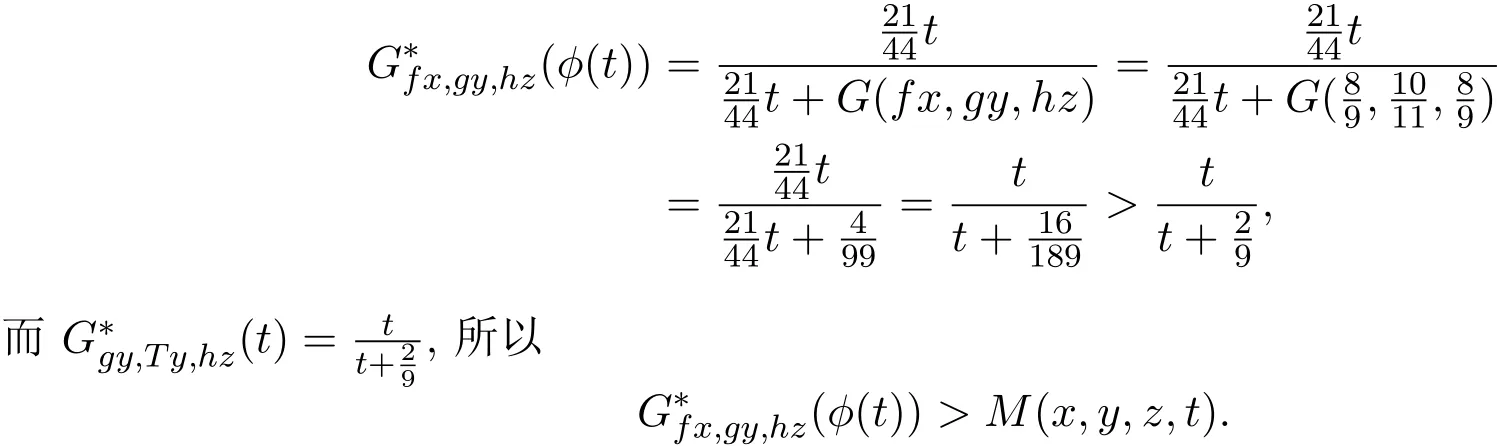
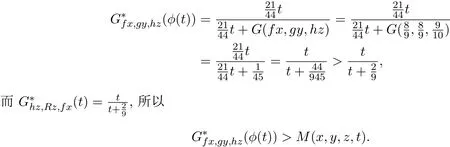

因此,定理2.1的所有条件全部满足,从而由定理2.1知,f,g,h,R,S和T在X中有唯一的公共不动点.事实上,可以验证:是它们唯一的公共不动点.
在定理2.1中,令S=T=R=I,I是恒等映射,则可得到如下推论.
推论 2.1(X,G∗,∆m)是一个完备的 Menger PGM-空间,其中 ∆ 是连续的 H-型 t-范数,假设自映射f,g,h:X→X满足下列条件:

其中x,y,z∈X,t>0,且ϕ∈Φ.则f,g和h在X 中有唯一的公共不动点.
在定理2.1中,令 ϕ(t)=kt,0 推论 2.2(X,G∗,∆m)是一个Menger PGM-空间,其中 ∆是连续的H-型t-范数,假设自映射f,g,h,R,S,T:X→X满足下列条件: (i)f(X)⊂T(X),g(X)⊂R(X),h(X)⊂S(X); (ii)S(X),T(X)和R(X)有一个是X的完备子空间. 则映射对(f,S),(g,T)和(h,R)在X中有存在公共的重合.更进一步的,若映射对(f,S),(g,T)和(h,R)是弱相容的,则f,g,h,R,S和T在X中有唯一的公共不动点. 在推论2.2中,令S=T=R=I,I是恒等映射,则可得到如下推论. 推论 2.3(X,G∗,∆m)是一个完备的 Menger PGM-空间,其中 ∆ 是连续的 H-型 t-范数,假设自映射f,g,h:X→X满足下列条件: 注 2.2 本文定理2.1与文献[6]的定理3.1相比,主要创新在于:文献[6]的定理3.1要求三对映射中至少有两对满足公共(E.A)性质,而本文定理2.1的条件中并不需要映射对满足公共(E.A)性质.另外,本文定理2.1的压缩条件也不同于文献[6]的定理3.1. 下面给出一个不能使用文献[6]的定理3.1,但可以使用本文定理2.1的例子,用以说明本文定理2.1的重要性. 例 2.2设X=[0,1],定义函数 为 其中 容易证得 (X,G∗,∆m)是一个 Menger PGM-空间,令 ϕ(t)=,ϕ∈ Φ,又定义 f,g,h,S,T和R:X→X如下: 容易得到映射对(f,S)和(g,T),(g,T)和(h,R),(f,S)和(h,R)都不满足公共(E.A)性质,因此不满足文献[6]中定理3.1的条件. 显然,映射f,g,h,S,T和R在X中不是G-连续的, 且S(X),T(X)和R(X)都是X的完备子空间.因此满足定理2.1中的(i)(ii). 下面证明映射f,g,h,S,T和R满足定理2.1中的(11)式,设 因此,满足定理2.1的(i)(ii)和条件(11),从而由定理2.1知,映射对(f,S),(g,T)和(h,R)在X中有公共重合点.事实上,易知1就是它们的公共重合点.