关于黑体辐射曲线顶点问题的讨论*
韩克祯 耿雪 张芳 葛筱璐 刘晓娟 秦华
(山东理工大学物理与光电工程学院 山东 淄博 255049)
物理学家Max Planck 于1901发表在德国《物理年鉴》的论文中,提出了与经典电磁场理论完全不同的辐射能量量子化假设[1](网络上有英文翻译版,如加拿大英属哥伦比亚大学的网页[2]),得到了在低频和高频电磁波段都与实验结果符合的黑体辐射公式,成功地开启了物理学的新纪元.Planck黑体辐射公式在原子物理学[3]、量子力学[4]和激光原理[5]等本科课程中都有提及,是本科阶段教学中一个重要的知识点,在从经典电磁学到现代物理学的过渡中起到了承上启下的衔接作用.
1 普朗克黑体辐射曲线顶点对应的频率和波长的困惑
Planck黑体辐射公式中,黑体辐射能量体密度按照频率分布和波长分布的公式分别为
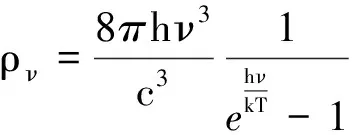
(1)
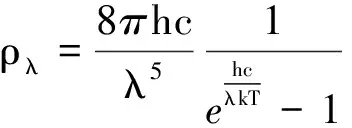
(2)
ρν(ρλ)的物理意义为:热力学平衡状态下,热力学温度为T时,黑体的电磁辐射在频率ν处(波长处)、单位频率间隔内(单位波长间隔内)的能量体密度.因此,式(1)和式(2)可以写为
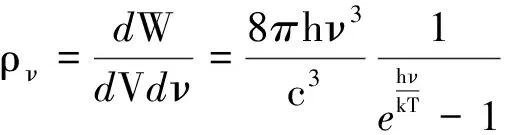
(3)
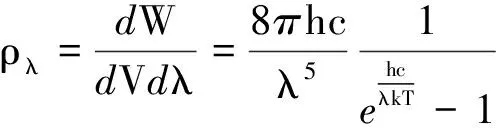
(4)
以温度为3 000 K为例,处于热平衡状态的黑体,其辐射能量体密度按照频率分布和波长分布函数ρν和ρλ的曲线如图1所示.
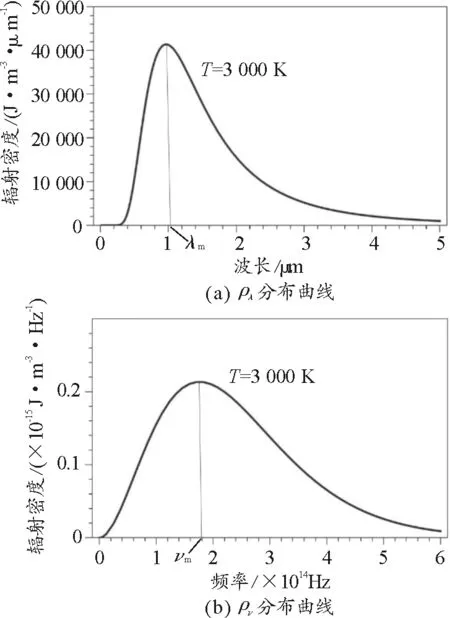
图1 黑体辐射能量体密度分布(T=3 000 K)
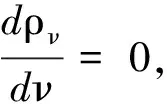
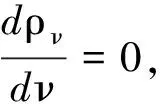
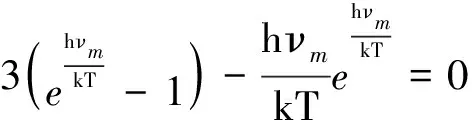
这是一个超越方程,其数值解为
即黑体辐射能量密度极大值对应的频率
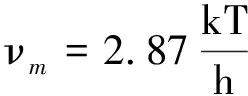
(5)
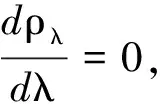
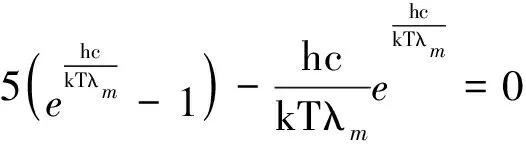
这也是一个超越方程,其数值解为
即黑体辐射能量密度极大值对应的波长
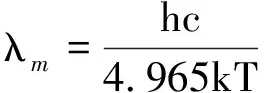
(6)
从上式可以得到
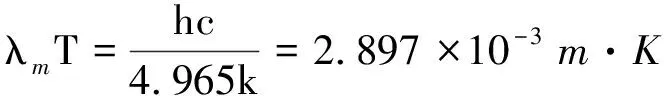
(7)
式(7)正是著名的维恩位移定律[3]. 很明显
即
乍看之下,该结果令人疑惑:对于给定的热力学温度T,黑体辐射能量密度取极大值时的νm和λm竟然不是对应的?
2 人们对该问题的认识现状
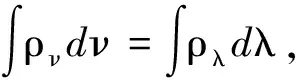
3 本文的分析讨论
我们经过思考分析之后,关于这个问题得到以下几点认识.
(1)ρνdν=ρλdλ是正确的.
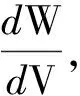
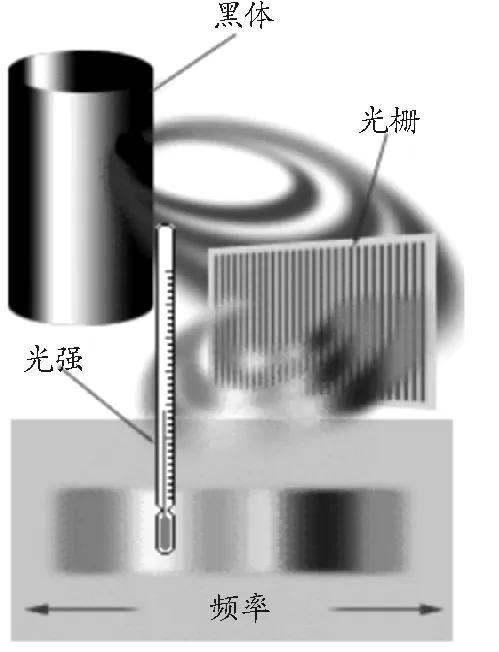
图2 黑体辐射能量体密度分布函数测量过程示意图[9]
因此,我们认为文献[7]是不合适的. 实际上,我们可以通过关系式
以及
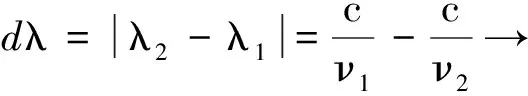
这两个关系式,从表达式(3)得到式(4),或者从表达式(4)得到式(3).
(2) 我们认同文献[8]的观点,黑体辐射能量密度取极大值时的νm和λm不相对应的根源来自于波长和频率不是线性关系. 鉴于文献[8]仅一句带过,本论文中我们进行详细说明如下.
我们利用Mathematica软件作图进行辅助说明,如图3所示.
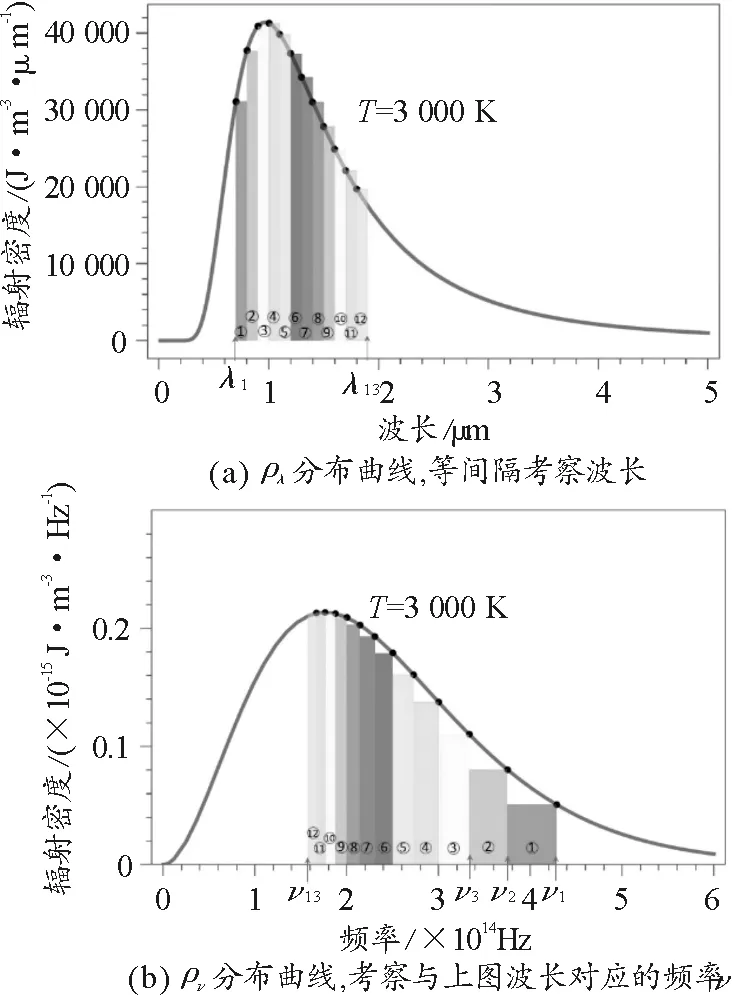
图3 黑体辐射能量体密度分布的深入理解(T=3 000 K)
在波长表示的ρλ分布曲线上,取等间隔分布的13个波长,从小到大依次为λ1,λ2,…,λ13,相邻两个波长之间的柱状图依次用1~12表示,如图3(a)所示. 容易发现,图3(a)的曲线顶点对应的波长在λ4附近. 根据黑体辐射体密度波长表示的定义
以及
与λ1,λ2,…,λ13对应的频率ν1,ν2,…,ν13则是不等间隔并且是从大到小反向排列的,这一点在图3(b)中有明显体现. 根据黑体辐射体密度频率表示的定义
我们发现,由于ν1,ν2,…,ν13是不等间隔的,其曲线顶点对应的频率不是在ν4附近,而是在ν11附近.
(3) 结合上面(1)和(2)的说明可以发现,维恩位移定律对应于黑体辐射能量密度的波长表示. 并且为了避免引起困扰,建议以后对黑体辐射的Planck公式加上说明,分别为“波长表示的黑体辐射公式”和“频率表示的黑体辐射公式”.
4 结论
本文揭示了黑体辐射曲线顶点在频率表示和波长表示下看似矛盾的根源所在,并结合Mathematica作图进行了直观详细地说明,有助于学生深刻理解黑体辐射能量密度ρν和ρλ的物理意义并培养学生精准理解物理概念的习惯和科学素养.我们希望本文能够给该问题带来的困扰画一个明了的休止符.

