基于风电的两种概率潮流计算的比较与分析
蒋炜华,赵 斌
(河南工学院, 河南 新乡 453003)
引言
随着风力发电在我国的大力推广,风电机组在并网运行时除了给电力系统带来如电压波动、谐波污染等问题外,还会影响电网运行的稳定性。许多大型风电场直接接入到电力系统中,不但使得线路之间的传输功率发生改变,还增加了节点电压的越限概率。这些不确定的因素会给电力系统规划和运行带来很多的问题。目前常用的概率潮流评估方法可分为两类[1-3]:解析法(point estimate method,PEM)和模拟法(Monte Carlo simulation,MCS)。蒙特罗法只有在大规模采样的条件下才能提高精度,而且计算量较大,不能节省成本。解析法得到输出变量的随机变量波动部分与输入变量波动之间的近似线性关系,快速地给出输出随机变量的分布。因此本文将基于半不变量法Gram-charlier相结合的方法,从而解决蒙特卡洛存在的问题,并带入IEEE-14节点验证此方法的正确性。
1 蒙特卡罗概率潮流计算法
蒙特卡罗法是根据抽样统计量或参数的值,用计算机产生抽样的结果,随着样本次数的增多,得到的各次统计量或者参数的估计值求得的平均值才能稳定。
基于蒙特卡罗法的概率潮流计算方法如下:

Pij、Qij分别为节点 i和 j注入有功和无功;Gij、Bij分别为系统导纳矩阵元素的实部和虚部;θij为节点i和j的相角差,可以概括为:

式中为 W=[w1,w2,…wn,]节点注入量,包括节点注入的有功功率和无功功率,X=[x1,x2,…xn,]为节点的状态变量,包括各节点的电压幅值和角度,f为潮流计算的方程组。
设节点i注入功率wi的概率分布函数为:

得到采样规模为m阶的系统节点注入功率样本矩阵如下所示:
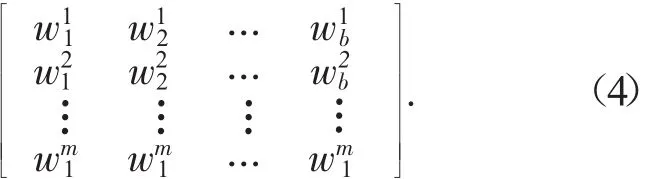
设系统有l条支路,采用上式对系统状态矩阵的每一行元素进行计算。支路矩阵可以概括为:

Z为支路潮流(包括有功,无功),g为支路潮流方程。
通过对系统矩阵和支路矩阵进行数字统计得到它们的概率分布和数字特征。当采样规模越大时,拟合度才会越高,但是计算量大,耗费时间多。
2 Gram-Charlier级数
2.1 半不变量法
半不变量γk又称累积量[4-5],是通过随机变量的特征函数取对数而得到的。式中αk,βk为随机变量x的阶原点和k阶中心矩,k=1,2,…,分别定义为xk和(xk-α1)的数学期望,一阶原点矩 α1,即变量均值 μ,二阶中心矩β2即变量方差σ2。
半不变量具有可加性,若有m个相互独立的随机变量,它们r阶半不变量都存在。当和Gram-Charlier(C-GC)相结合时:已知随机变量x的μ和σ的值,利用对其进行标准化,则z的概率密度函数可表示为标准正态分布概率密度函数φ和它的各阶导数线性组合,即Gram-Charlier级数,系数Ak表示如下:
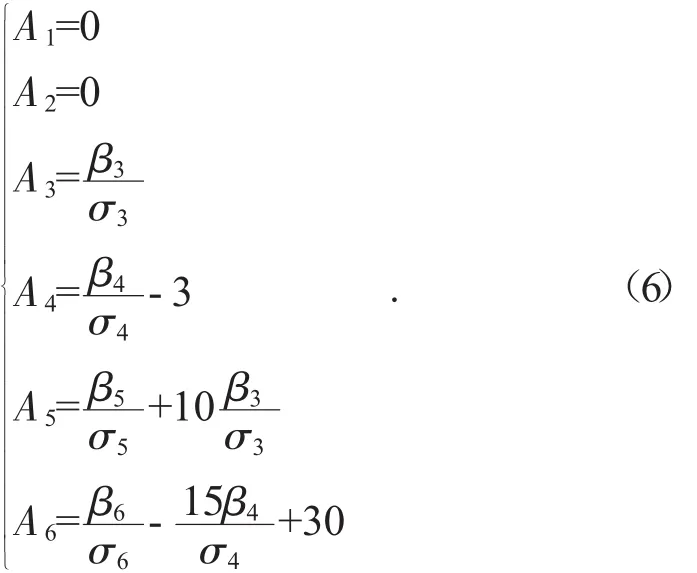
在精度范围内,可对级数进行截尾,可得到起分布的近似表述,如本文算例取到k=6。
得到随机变量z的概率分布近似表达式f(z)后,可以由x与z的关系x=σz+μ,求得随机变量x的概率密度函数:

2.2 Gram-charlier级数展开
Gram-charlier[6]根据Hermite多项式的正侥幸展开,因而又称正交展开式。根据Gram-charlier级数展开,随机变量的累积分布函数可表示为:

3 随机潮流的系统模型
在确定性潮流计算中,已知的量包括平衡节点外所有的有功注入量、所有的PQ节点i的无功注入量,所有的PV节点的电压幅值。待求得量包括平衡节点的有功和无功注入量,所有PQ节点的电压幅值和相角,所有的PV节点的无功注入量和电压相角。其中潮流方程表示为:

其中,δi为节点的电压相角,i=1,2,…,n;设 S=[P1,…,Pn,Q1,…,Qn]T,X=[U1,…,Un,δ1,…,δn]T,则式可表示为:

采用牛顿-拉夫逊法,经迭代求解后,可以得到初始状态变量和初始注入功率值X0初始值S0.
式中经过泰勒级数化简得到如下形式:

忽略式中的最高项,可得

其中:ΔZ=[ΔP,ΔQ]T。

此时,定义K0为K0=D0J-10,D0是一个2m×2n阶的矩阵,m为支路数。由于J0和D0均为常数矩阵,因此K0亦为常数矩阵,即线路输送功率和节点注入之间存在线性关系。
4 仿真算例及结果讨论
本例算例以改进后的IEEE-14节点系统作为研究对象和采样值10 000次的蒙特卡罗作比较。在系统节点IEE-14中加入风电系统,分析该方法的有效性,具体分布如图1所示:

图1 IEEE-14节点系统图
4.1 风速模型
本文采用其函数表达式为:

式中:v为随机风速;k,c分别为Weibull分布的形状和尺度参数。
4.2 负荷的模型
母线负荷可以用正态分布表示:

式中:x表示节点负荷;μ和σ2表示该分布的期望和方差。
4.3 算例比较
为了验证GSLHS的有效性,本文将GSLHS和G-CG以及CSMCS进行PLF计算结果进行对比;假设采用10 000次的CSMCS方法进行PLF计算得到的结果是精确的,输出随机变量的期望值和标准差分别用μacc和σacc表示。类似地,将上述几种方法在小规模采样情况下进行PLF计算得到的输出变量的期望值和标准差分别用μsim和σsim表示,用输出变量的期望值和标准差的相对误差和表征PLF结果的精度,计算公式为:

在PLF的输出结果中,每类变量的数量都不止一个,例如不同节点的电压幅值、有功功率。为了表示算法的收敛情况,将每种输出变量的相对误差的平均值ζμ和ζσ来表示输出变量的误差情况。此外,由于PLF计算过程是波动的且具有随机性,为了准确评价本文提出的PLF评价本文提出的PLF计算方法的性能,取100次PLF计算结果平均值作为最终计算结果。

图2 支路9-10有功功率的CDF曲线对比
本文采用GSLHS,G-CG的概率潮流计算和蒙特卡洛概率法进行比较,G-CG和GSLHS在采样400次和蒙特卡洛法10 000次的精度相同,所以GSLHS在相同采样规模下,能够达到更好的效果。
由图2和图3中得出,相对于半不变量法,拉丁超立方法(GSLHS)得到的电压概率密度函数和有功功率密度函数得到的图像和蒙特卡洛模拟10 000次相比更加吻合,所以验证得出此方法是有效的,因此次方法可以作为概率潮流的方法之一。

图3 支路9—10有功功率的PDF曲线对比
5 结论
本文通过拉超立方的方法和半不变量法相比较,得出该方法能在相同规模下,能够更好地降低采样规模,提高精度。在较短的时间内得出各节点的电压越限概率以及支路的潮流分布情况,因此可以作为计算概率潮流的有效方法之一。

