基于混合范式多任务学习的图像稀疏表示

宋正丹, 崔荣一, 怀丽波, 金小峰

(延边大学 工学院, 吉林 延吉 133002)

0 引 言

评价机器学习算法的优劣主要考察其在处理未知样本时的泛化能力。传统机器学习算法主要是针对单任务学习, 然而当实际应用中遇到训练样本不足, 往往会出现欠拟合现象。在机器学习和计算机视觉领域中, 如果可以学习到多个任务中的共享隐藏信息, 利用这些任务之间的相关性可以大大提升算法的学习性能[1]。

生物视觉认知研究发现并证明, 人类在接收自然图像时, 视觉系统总是在已知的视觉字典中, 利用少数元素, 寻找一个最近邻的基的稀疏表示, 因此, 稀疏表示问题可以被看作为是通过线性回归模型对特征的稀疏选择[2]。这种对查询的重构稀疏线性表示方法在信号处理和计算机视觉中引起广泛关注。近年来, 稀疏和组稀疏已经被成功应用于机器视觉和图像处理的稀疏表示中[3-6]。

正如Wright等[7]在人脸识别中证明的, 只要训练样本特征足够, 通过对训练样本特征的线性组合, 测试图像则可以被稀疏表示。传统的多任务学习模型是基于任务相关假设为前提, 但在实际应用中, 不可能每个任务都与所有任务紧密相关, 在这种情况下, 与无关任务共享信息可能会降低模型的性能, 这种现象称为负迁移(Negative Transfer)[8]。目前也相继出现提取任务之间负相关信息的方法[9], 证明了互斥的稀疏性可以提高特征在分类中的竞争性。然而Lasso模型忽略了任务之间的潜在关系, 选择产生太多的冗余信息, 容易引起数据的过度拟合； L2,1范式正则化的多任务模型, 太过于严格要求所有任务之间的共享关系, 忽视了少数任务之间不相关却具有共同有用信息。文献[10]认为任务之间存在聚类或组关系, 但忽略了组与组之间的互斥互补关系, 从而损失了特征选择的更多判别性。

针对以上不足, 笔者将多特征稀疏表示的可行性推广于多任务学习, 提出一种联合稀疏表示的去相关多任务学习框架(DMTJSR: Decorrelating Multi-Task Learning Joint Sparse Representation), 方法的核心思想是使不同特征之间对整幅图的表示不仅具有互补性能, 而且不同特征之间相对独立, 去除任务之间的冗余关联。不同于传统多任务学习, 严格地要求所有不同任务要保持统一的关联性, 在此框架下, 笔者将同一种类型的特征视为具有组关系的任务： 组内提取同种特征任务的共享相关信息, 即特征只共享相同稀疏模式, 但稀疏系数不同； 组间去相关, 增加不同种类特征选择的竞争性, 即组间选择互斥, 具有不同的稀疏模式, 由此, 同时保证了特征的局部性信息和判别性, 为图像分类提供了有用信息。

1 多任务学习模型

笔者在实验部分作为对比基准的两种经典方法; 一种是单任务的稀疏表示Lasso(Least absolute shrinkage and selection operator)模型; 另一种是L2,1范式多任务组稀疏模型。

1.1 稀疏表示Lasso模型

在Wright等[7]的SRC(Sparse Representation Classification)中, 测试样本由训练样本近似线性表示,W为系数。假设Y是一个N维的特征提取描述子,Y=[y1,…,yM]∈RN×M,i∈1,…,M,D∈RN×Q为视觉字典基集合, 目标函数被定义为

(1)

其中W=[w1,…,wM]∈RQ×M,wi是对yi的编码,λ是正则化参数, 保证稀疏度。式(1)的第1项为损失函数, 即反映了原始特征与重构特征的均方误差, 它衡量了编码描述的好坏程度, 这里设定为最小二乘损失函数, 第2项‖W‖1是凸正则稀疏约束项, 为目标函数的惩罚函数, 它保证了整个模型可以很好的得到近似稀疏解, 也就是保留了最具有竞争力的特征。L1范式是对0范式的放宽处理, 使函数变成了最优凸近似, 通过惩罚函数项λ‖W‖1可以看到,W的每列wi将会在L1范式的约束下变得稀疏。

1.2 L2,1范式多任务组稀疏模型

不同于Lasso模型, L2,1模型则更严格要求提取所有任务的共享模式。在多任务框架下, 模型由K个任务组成, 认为训练样本X=[X1,…,XK],k=1,…,K,Xk∈RNk×Q,Q为样本维度,Nk为样本数量,Y=[y1,…,yK],yk∈RNk×1是由Xk内每列原子线性组合对应的响应。多任务目标函数被表示为二次损失函数的最小化问题为

(2)

其中W=[w1,…,wK],W的每列wk∈RNk×1为系数,λ同样为正则化参数。前1项是由最小二乘函数构成的损失函数, 第2项正则化稀疏约束项‖W‖2,1采用的是一个L1和L2范式的混合范式作为惩罚函数, 它先通过对W的行向量计算L2范式, 得到列向量v=(a1,…,aQ)T, 再对其求L1范式, 使W矩阵中只能有很少的非零行存在, 由此保证了特征共享信息[11], 此外, 向量v也体现了每个特征的重要性。

2 联合稀疏表示的去相关多任务学习框架

2.1 DMTJSR学习模型

当训练样本不足时, 多任务学习可以充分发挥任务之间的关联, 提高泛化能力, 然而对于小样本分类问题, 系数的稀疏性对分类准确率并没有实质的帮助。因此, 为得到既保证稀疏性同时也能保证不破坏图像的本质信息, 提高图像表示性能, 利用先验信息, 指出相关任务和不相关任务。笔者所利用的先验信息希望做到： 同一种特征是相关任务, 在学习过程中能尽量提取出相关任务的相关信息； 不同种类特征之间是不相关任务, 尽量避免不同任务所带来的冗余影响, 在不同任务间去相关。基于此物理意义, 混合L1范式和L2,1范式, 定义了一种折中式(1)和式(2)方法的目标函数。此方法更具有语义信息和物理意义, 它不仅保留了L1范式的更具有竞争力诱导[12], 同时也在每个任务组中使用L2,1范式, 提取同种特征的共享信息。目标提取效果如图1中W效果, L2,1范式组内约束使得出现了一整行保留, L1组间约束使得出现不同组互补交叉的现象。

图1 DMTJSR的工作机理Fig.1 Mechanism of DMTJSR

假设从一幅图片中提取了K种特征(如颜色, 纹理), 定义D=[D1,…,DK],k=1,…,K,Dk∈RNk×Q为每种特征相应的字典集合,Nk为每种特征描述子的维度,Q为固定字典规模, 图像提取K类特征描述子集合Y=[Y1,…,YK],Yk∈RNk×Mk,M=M1+…+Mk+…+MK,Mk为每种特征描述子集合矩阵大小, 则DMTJSR的目标优化函数为

(3)

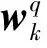
2.2 优化方法

笔者中由于不同特征数据结构、数据大小分布不同, 采用不同稀疏约束参数μk调整稀疏程度。μk约束了每个特征组任务内稀疏度, 提取组内共享信息；λ′约束组间稀疏度, 由此达到不同特征之间的竞争性。

采用文献[13]中组稀疏迭代方法作为式(3)的优化方法。因此, 式(3)可被改写成

(4)

DMTJSR中的L2,1,1混合范式虽然是凸函数, 但在式(4)中仍是非光滑, 且是非平凡的[14]。将式(4)中混合范式L2,1,1平方部分近似为其上限[11], 由于

(5)

(6)

则目标模型(4)被改写为凸光滑函数

(7)

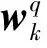
输入： 测试图像多种特征描述子Y=[Y1,…,YK], 多特征训练字典D=[D1,…,DK]。

初始化：Z(0)=Z(1)=W(0)=D-1×Y,t0=0,L0>0,η>1.

迭代：i=1,2,…,Li=ηLi-1直到W收敛:

更新W(i),k=1,…,K,W(i)=Z(i)+(t(i-1)-1)(Z(i)-Z(i-1))/t(i)

输出：W=Z(i+1)。

式(8)可由软阈值操作法[16]按照近似

W=sign(w)max(0,|w|-λ/L)(9)

对Z按任务(K)和行(Q)逐步求得, 此方法最大的优势就是, 可以很快地提取到稀疏解。对于每次迭代, 计算耗时主要是在损失函数的梯度求解和式(8)最小化求解上。计算梯度的时间复杂度为O(Q2M), 式(8)的时间复杂度为O(QK2), 因此DMTJSR整体运算时间复杂度为O(Q2M+QMK2)。在笔者多特征提取中M≫Q≫K。

3 实验结果及分析

笔者进行了多组分类实验来评价DMTJSR稀疏表示的性能, 同时, 为了证明多任务学习在样本不充分条件下的优势, 实验选择了小样本数据集caltech101。实验中, 对每类样本集中随机选取1/2用于训练, 余下的再随机取1/4分别作为验证集和测试集。

3.1 多特征提取

对于整个数据集笔者提取了SSIM[17], Dense SIFT[18], LAB颜色特征和GB[19]四种特征。除颜色特征外, 其余特征提取方法均在灰度图像上进行操作, 全局特征选择在像素10×10, 步长为8的图像网格计算。通过K-means算法, 对所得到的整幅图像提取到的每种特征集合聚类, 聚类中心作为视觉词汇, 分别形成对应不同特征的字典Dk。由于此方法所获得的视觉特征存在一词多义的情况, 字典大小太大会增加字典的过多冗余信息, 太小会导致信息不足, 综合以上两点笔者根据训练样本大小, 选择较合适的500作为字典默认大小[20]。

3.2 特征选择

特征的稀疏表示, 可以看作是对特征的稀疏选择, 参照人视觉系统, 如何利用尽量少的特征能最好地表达出原始图像是图像稀疏表示的关键。

在使用多特征混合进行分类时, 由于各个特征对于图像的贡献不同, 其权值也应该不同, 如何确定各个特征的参数也是其中重要一步。针对不同结构的特征数据, 统一λ时, 特征选择时很难达到同时稀疏, 这是由于若某一特征数值过大会直接全部抑制另一特征, 使模型失去了竞争关系的物理意义, 也就是在稀疏条件约束时, 特征之间不存在公平竞争； 归一化λ时, 虽可以达到公平性, 但其容易影响损失函数的准确度从而降低分类性能。因此, 笔者设置相对应的正则化参数μk, 以此达到4种特征可同时稀疏的效果, 同时也保证特征选择的有效性。μk和λ′的选择采用交叉验证获得, 初始化为1, 从1～10, 以步长为0.2增加, 寻找最优参数, 通过对比实验结果最终确定。

采用相同的实验数据, 分别对比了DMTJSR、 Lasso和L2,1模型的稀疏化效果。部分截图参见图2～图4, 其中矩阵由黑色矩形表示, 非零元素用白色块表示。

图2 统一λ稀疏效果 图3 归一化λ稀疏效果 Fig.2 Unified λ sparsity Fig.3 Normalized λ sparsity

图2和图3分别为DMTJSR统一λ和归一化的稀疏效果。前者稀疏效果并不理想, 而后者在使数据结构归一化后相同的情况下, 则可以达到较理想稀疏状态。

图4比较了不同多任务模型的提取效果, 图4a为DMTJSR调节μk的稀疏效果, 达到了笔者理想稀疏效果, 即多特征之间彼此不相交且互补。Lasso模型主要是为了去除少部分多余可能特征的选择, 没有借鉴任务之间的有利相关信息, 可看出图4b中仍具有太多冗余信息, 同时过度强调特征之间的竞争关系, 损失了许多有用信息； L2,1模型则硬性要求所有任务中所有特征参与共享信息的提取, 即如果一种特征的某一视觉词汇被选择, 则其他种类的特征都要选择这一位置的视觉词汇, 导致图4c中的很多直线部分。相比而言, DMTJSR是寻找相关任务之间的共享信息同时保证尽量选择更少的重复相关特征, 在特征选择上更具有互补性, 在拥有了多特征组结构的先验知识, 可以很清晰地在图4a中看到它抑制了不同组之间的相关性。

a DMTJSR稀疏效果 b Lasso模型稀疏效果 c L2,1模型稀疏效果图4 部分W矩阵在不同模型中的特征提取效果Fig.4 Part of matric W on different models about extracting features

3.3 分类性能

稀疏表示已成功的被用于图像重构、 压缩、 修复等应用中, 却对图像分类没有很好效果, 因此笔者利用分类效果作为评价方式, 为更好地说明算法的有效性。

当K=1时, DMTJSR直接退化为SRC, 因此, 直接使用SRC的类似分类方法, 计算测试样本与重构值的损失函数, 最后将测试样本分为损失函数最小的类别中。分类准则即为

(10)

本节采用固定字典, 只针对图像稀疏系数的学习。将传统经典分类方法SVM、 LDA和SRC作为笔者算法的分类准确率评价基准, 进行了单任务之间、 单任务与多任务之间和多任务算法之间的对比实验。参数设置采用交叉验证获得[7,21]。

表1为在DMTJSR多任务学习框架下4种多特征联合与单任务在SRC模型中实验结果对比, 可以观察到多种特征任务联合学习的性能都要超过单个特征任务, 并且在特征具有足够代表性的情况下, 分类性能会大幅度提升。实验结果证明, 多种特征对学习图像的特征表示都具有一定的贡献, 可以充分提高特征表示能力, 多特征联合图像表示性能明显优于单特征。同时验证了DMTJSR模型学习算法的有效性, 可以充分利用多特征间的有效信息学习到图像特征表示。

表1 单任务与多任务分类精度对比

为了证明并验证DMTJSR的分类有效性, 笔者进行了两组对比实验, 一组是通过与SVM, LDA, ScSPM[22]和LLC[23]以及多类别分类算法KMTJSRC[8]几种经典方法对比多特征情况下的分类性能, 对于单任务分类器多种特征选择直接串联方法； 二组是对比在ScSPM和LLC单任务时的最佳性能, 验证多任务对分类的必要性。从表2对比实验结果可知, 一组： 笔者实验结果超过了目前经典方法, L2,1,1多任务学习模型的有效性在对比中有很明显的优势, 准确率高且方法简单, 同样在时间复杂度方面, L2,1,1多任务学习模型算法效率更高； 二组： ScSPM和LLC稀疏编码与金字塔匹配结合, 大幅度提高了图像分类性能, 在分类领域内得到了广泛关注, 由于二者都是在提取单任务特征dense sift的情况下就可以得到较好的分类准确率, 因此为证明多任务的必要性和算法的优势与单任务的ScSPM和LLC做了对比, 实验结果证明此两种方法不适合多特征应用, L2,1,1多任务学习模型相比于二者单任务下较高的分类准确率都有所提升, 鲁棒性更强, 说明了多特征有效联合的必要性, 它可有效提高图像表示能力。另外, 此分类方法格外优于ScSPM和LLC算法的是无需学习分类器, 很容易扩展类型和添加新样本, 特别是增量学习框架, 可以扩展到其他各类特征。

表2 不同分类方法性能对比

在学习样本稀疏性时往往会损失掉图像的有用信息, 从而导致在图像分类性能上的不足, 在与多任务Lasso模型和L2,1模型对比中, 前者会提取出过多冗余信息, 后者则过于严格要求所有特征参与共享同一种稀疏模式, 这些不足都影响了分类精度。DMTJSR是二者的折中方法, 充分了提取出了不同种类特征的各自有优势, 使特征表示更具有鲁棒性, 对比实验结果如表3所示, 体现了DMTJSR既保证了样本的稀疏表示的优点, 也提高了图像分类的准确性, 保留了图像有用信息, 证明了DMTJSR的优势。

表3 多任务模型性能对比

表3中Lasso模型和L2,1模型的损失函数(误差函数)远远大于笔者算法, 由此可以得出DMTJSR对图像重构也具有积极作用。这是因为, 要得到模型的全局最优解需要数百次的迭代, 而DMTJSR算法收敛时不需要每次都迭代到全局最优解, 只要满足分类条件即可, 即损失函数最小, 因而算法时间效率高, 重构误差小, 这也是其他分类器, 如SVM(Support Vector Machine)、 Logistic regression等都不具备的。

4 结 语

笔者提出了一种基于混合范式多任务学习的图像稀疏表示学习框架, 算法将不同种类特征归为任务组, 实现组内共享信息, 组间最大竞争。它是一种简单而有效地联合多特征的视觉特征提取方法, 并且提高了分类准确率。为了评估性能, 笔者做了多组对比实验, 在单任务之间、单任务与多任务之间以及多任务之间, 笔者方法都优于现已成熟算法, 足以证明联合稀疏表示的去相关多任务学习框架DMTJSR的有效价值。

在以后的研究中将扩展如何能自适应的调节字典, 使得字典特征更具有判别性和局部性。并扩展到其他类型数据中和方法研究中。