矿井下分布式光纤定位精度及感测距离研究

郭继坤, 陈司晗

(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)

0 引 言

中国是世界产煤大国, 同时煤炭行业属于高危行业, 煤矿重大特大事故时有发生, 如何快速有效地解救被困人员对煤矿安全生产有重要意义[1,2]。光纤因其无源、 抗电磁干扰等优点被广泛应用于井下定位问题[3-6], 煤矿井下分布式光纤定位系统, 通常采用的定位方法是基于双Mach-Zehnder干涉仪的分布式光纤定位技术, 并通过时延估计的方法进行定位。由于瑞利反向散射(RB: Rayleigh Backscattering)噪声严重降低了信号的信噪比(SNR: Signal Noise Ratio), 导致定位精度较低, 限制了定位感测距离[7-9]。为提高井下定位精度和感测距离, 笔者提出了一种基于非对称双Mach-Zehnder干涉仪的分布式光纤振动传感技术, 利用DFB(Distributed Feedback )和DWDM(Dense Wavelength Division Multiplexing), 并通过SVD的互相关时延算法, 实现精准定位和扩大感测距离。

1 系统结构及原理

笔者研究的非对称双Mach-Zehnder分布式光纤振动(ADMZI: Asymmetric Mach-Zehnder; Inter-ferometer)传感系统, 其结构与改进前的双Mach-Zehnder分布式光纤振动(DMZI: Mach-Zehnder; Inter-ferometer)传感系统, 区别在于光源(Source)采用分布反馈激光束(DFB: Distributed FeedBack), 在光环形器(C)和光电探测器(PD: PhotoDetector)之间接入密集波分复用(DWDM: Dense Wavelength Division Multiplexing), 结构如图1所示。

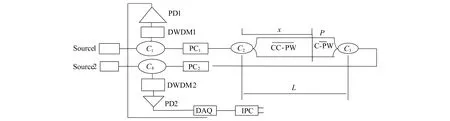
图1 ADMZI感应系统Fig.1 ADMZI sensing system

在图1中, ADMZI系统由数据采集卡(DAQ: Data Acquisition)、 工业个人电脑(IPC: Industrial Personal Computer)、 3 dB光纤耦合器(C2,C3)、 光环行器(C1,C4)、 极化控制器(PC1,PC2)、 密集波分复用器(DWDM1,DWDM2)、 光电探测器(PD1,PD2)等组成, C-PW, CC-PW为顺时针和逆时针传播的主波。两台Mach-Zehnder干涉仪在两个不同的波长λ1和λ2下工作并且波长差值大于0.8 nm, 波长都接近1 550 nm, 并通过PC1和PC2进行可见性补偿[4]。在CCW方向的传感光纤中, 光信号通过C4-C3-C2-C1的传播过程到达PD1, 并经DWDM1滤波。DWDM1对λ1的后向瑞利散射有去噪作用, 使λ2的逆时针光波信号能顺利通过, 可获得逆时针方向的高信噪比, 提高定位精度。

将光纤铺设于巷道, 假设振动发生在P点。由于从点P到PD1(CCW)和PD2(CW)的距离通常不同, 因此会有时间延迟d[10-13]。因为输出的两波长不同, 为避免错误估计, 所以假定观察时间很短, 环境噪声几乎不变。振动定位解调的关键是估计来自两个信道的信号之间的时间延迟[4]。

由图1可知, 时间延迟d可表示为

d=2n(L-x)/c(1)

其中x是扰动位置,c是真空中的光速,n是光纤中的有效折射率,L是感测长度。因为c,n和L都是常数, 所以,x可以由d推出[14-16]。用上述方法求取的时间延迟d误差较大, 为减小误差常采用互相关时延算法求取时间延迟d。

2 互相关时延算法

设y1(t)和y2(t)为两个信号,n1(t)和n2(t)为噪声[4], 则y1(t)和y2(t)的互相关函数可以表示为

Rxy(τ)=E[y1(t)y2(t+τ)](2)

则两个探测器输出的实际信号为

y1(t)=I1{1+cos[φ0+(1-K)Δφ(t-τ1)]}+n1(t)(3)

y2(t)=I2{1+cos[φ0+(1-K)Δφ(t-τ2)]}+n2(t)(4)

令s(t)=I1{1+cos[φ0+(1-K)Δφ(t-τ1)]}, 则式(3), 式(4)可化简为

y1(t)=s(t)+n1(t)(5)

y2(t)=ms(t-d)+n2(t)(6)

其中m=I2/I1, 将式(5), 式(6)代入式(2)得

Rxy(τ)=mRss(τ-d)+mRsn1(τ-d)+Rsn2(τ)+Rn1n2(τ)(7)

其中Rn1n2(τ)、Rsn2(τ)和Rsn1(τ-d)分别为噪声与噪声, 噪声与振动之间的互相关函数[17,18]。假设Rn1n2(τ)、Rsn2(τ)和Rsn1(τ-d)都为零, 则有

Rxy(τ)=mRss(τ-d)≤mRss(0)(8)

由式(8)可知, 互相关函数最大值处的τ即为所求的时延d。通过式(8)可知该算法的延时性能与信号的信噪比有关, 为最大限度地提高定位精度[4], 必须提高所获取信号的信噪比。为此, 笔者通过SVD(Singular Value Decomposition)算法对信号进行降噪处理, 提高SNR(Signal Noise Ratio), 结合互相关时延算法, 提高定位精度。

3 基于SVD的时延算法

3.1 基于SVD的信号降噪原理

由于外界环境的影响, 导致所测得的信号会受到不同程度的噪声污染[19-22]。通过采用SVD算法提取信号, 提高信噪比达到降噪的目的, 进而提高定位精度。

根据奇异值分解理论, 设矩阵m×n(m>n)为A, 秩为r, 存在m阶矩阵U和n阶矩阵V, 使

∑=UTAV(9)

其中∑为m×n非负对角阵, 且

(10)

其中σ1,σ2,…,σr和σr+1=…=σn=0为A的奇异值。若A为信号和噪声共同组成的矩阵, 则A有n个非负奇异值。即式(10)中的对角元素均为非负。保留前q个有效奇异值, 通过奇异值分解逆运算重构Am, 最后对Am的反对角元素求平均就可得到降噪信号。

基于SVD降噪原理实现步骤如下。

1) 构造一个由实测信号组成的矩阵, 设为

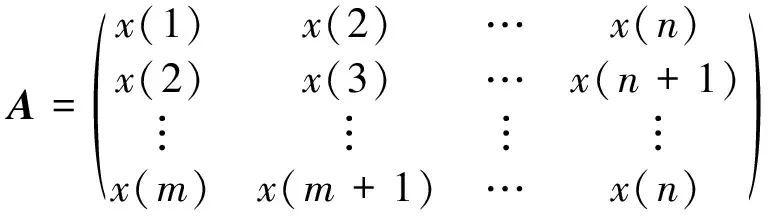
(11)

并对其进行奇异值分解得到U,V和Σ。其中m=N-n+1。

2) 保留Σ中的前q个有效奇异值, 其余奇异值置0, 得到Σ′。

3) 通过Am=UΣ′,VT进行奇异值分解逆运算, 得到重构矩阵Am。

4) 对Am中的反对角元素求平均得到降噪信号。

3.2 基于SVD的时延估计

基于SVD时延估计的基本方法是：

1) 对探测器接收到的两路信号进行SVD降噪, 提高SNR;

2) 将降噪后的信号通过互相关算法求时延。

流程如图2所示。

图2 基于SVD的时延估计流程图
Fig.2 Flow chart of time delay estimation based on SVD

4 实验与分析

本次实验的光源线宽为50 kHz, 分布式反馈激光束功率为5 mW。波长λ1和λ2分别为1 549.77 nm和1 550.89 nm。DWDM1和DWDM2的中心波长分别1 550.06 nm和1 550.85 nm, 通带宽度为±0.25 nm。在光纤某一位置施加振动信号作为振动源, 图3和图4分别给出了采用DMZI和经SVD降噪后ADMZI的振动位置信息。

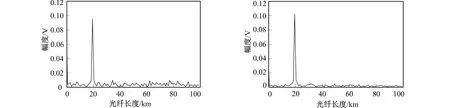
图3 DMZI振动曲线 图4 ADMZI振动曲线 Fig.3 DMZI vibration curve Fig.4 ADMZI vibration curve

由图3和图4可知, 在对振动事件的识别方面, 经SVD降噪后的ADMZI(Asymmetric Double Mach-Zehnder Inter-ferometer)分布式光纤振动传感技术与传统的DMZI(Double Mach-Zehnder Inter-ferometer)分布式光纤振动传感技术相比, 有较高的灵敏度, 更容易获取振动信息, 进而实现定位。

另外在上述实验的基础上光信号通过循环器(C1,C4)和偏振控制器(PC1,PC2), 再经耦合器C2和C3(均为3 dB耦合器)从相反方向耦合到马赫曾德干涉仪中。两路光纤检测器分别检测出两路输出干扰, 通过数据采集采样, 采样速率为10 MS/s。然后将数据用SVD进行降噪处理, 通过时延计算扰动位置。光纤干扰区域L的感测长度由1 km的一根光缆和5 km的裸光纤组成, 距离从1～61 km, 间隔为5 km。振动是通过敲击距C2(x=0.8 km)0.8 km处电缆产生的。ADMZI和DMZI都使用相同的器件和传感光纤。比较ADMZI和DMZI中的平均SNR和定位MSE(Mean Square Error), 如图5、 图6所示。

图5比较了在不同感测长度L处的SNR, 由图5可知, DMZI中的SNR总是较小, 比ADMZI下降得快。当L为61 km时, ADMZI情况下的SNR仅为9.91 dB, 比DMZI的情况SNR高20 dB。

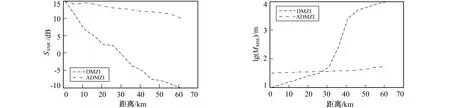
图5 DMZI和ADMZI不同距离的SNR 图6 DMZI和ADMZI不同距离的MSE Fig.5 SNR of different distances Fig.6 MSE of different distances between DMZI and ADMZI between DMZI and ADMZI

图6比较了在不同感测长度L处的MSE。当感测长度L小于26 km时, DMZI在MSE中表现更好, 在L=1 km时达到最小9.31 m。但当L大于26 km时, ADMZI的性能要高于DMZI。前一种情况下的MSE仅随L轻度增加, 而后者的MSE随L迅速恶化。当L为61 km时, ADMZI的定位MSE为51.2 m, 对于实际应用已经足够准确。从上述实验中得到的定位精度统计如表1所示。

表1 定位精度统计

由表1可知, 定位误差分布在0～20 m范围内的数据占51.6%, 分布在0～50 m范围内的数据占30.4%, 少数数据的定位误差大于50 m。定位误差的平均值和标准偏差分别为33.82 m和40.713 9 m。因此, 经SVD降噪后的ADMZI时延估计系统的定位误差基本可以达到0～50 m的范围。

5 结 语

针对矿井下分布式光纤定位精度低和感测距离短的问题, 笔者采用了DFB激光器和DWDM的非对称双Mach-Zehnder干涉测量结构(ADMZI), 利用SVD时延估计算法, 扩大了分布式光纤定位的感测距离, 提高了定位精度。通过实验分析, ADMZI结构在远距离传感方面比DMZI更具优势并且有更高的灵敏度。在61 km的感测距离处, ADMZI系统的信噪比为9.91 dB, MSE为51.2 m, 相比改进前的DMZI, 在感测距离和定位精度上都有显著提高。