TV—MCP：一种新的脉冲噪音图像恢复方法

白敏茹 龚世欢

摘 要：对于被脉冲噪音污染的图像恢复问题，广泛使用的TVL1模型会偏离数据获取模型和先验模型，特别是对高水平噪音.针对这个问题，基于MCP函数，提出了一种新的图像恢复模型，称之为TVMCP模型，并给出了该模型的近似逼近方法，从理论上证明了该算法的全局收敛到TVMCP模型的稳定点.对于近似逼近子问题的求解，采用交替方向方法求解.通过对多组图像在不同噪音污染水平下的数值仿真实验，验证了本文所提出的模型和方法的有效性.实验结果显示， TVMCP模型比TVL1模型能够取得更好的恢复效果，尤其是在高噪音污染的图像恢复问题上，TVMCP恢复图像的SNR值最高可以达到TVL1恢复图像的SNR值的两倍.

关键词：图象恢复；TVMCP；脉冲噪音；交替方向方法

中圖分类号：TP751 文献标志码：A

Abstract：For the problem of image restoration of observed images corrupted by impulse noise， the widely used TVL1 model may deviate from both the data acquisition model and prior model， especially for high noise levels. To overcome this problem， based on MCP function， a new model called TVMCP and its approximation method were proposed. It is proved that the approximation method converges globally to a stationary point of TVMCP model. Alternating direction method of multipliers was applied to solve the approximation subproblem. In the numerical experiments， TVL1 and TVMCP were applied to the problem of image denoising and deblurring in the presence of impulse noise， which verifies the effectiveness of the proposed model and method. The results show that TVMCP outperforms TVL1， especially for the high noise level image denoising. The maximum SNR value of TVMCP image restoration can reach 2 times that of TVL1 method.

Key words：image restoration；TVMCP； impulse noise； alternating direction method of multipliers

随着数字成像仪器的快速发展，智能手机、数码相机和各种监控设备等的普及，数字图像处理越来越靠近人们的生活.由于数字成像系统、感光元件、工作环境和处理手段的不完善，图像在生成、采集、处理和传输过程中受到损伤， 如低光照环境下长时间曝光过程中照相机抖动导致图像的模糊不清；高感光度引起的噪点；目标与成像器材间的相对运动产生的运动模糊；数字图像在生成、采集、数字化和处理过程中引入的噪声等，都将导致实际得到的图像出现图像模糊化、噪声污染甚至部分图像信息的缺失等问题.

根据噪音的统计分布特征，噪音可以分为脉冲噪音、高斯噪音和瑞丽噪音等，其中脉冲噪音是十分常见的一种，它通常在数字图像的存储和传输的过程中产生.脉冲噪音又分为椒盐噪音和随机值噪音.

对于被脉冲噪音污染的图像恢复问题，广泛使用的模型是由l1范数度量的数据保真项和全变分度量正则化项组成的模型（简称TVL1）[1-2].TVL1模型能够有效地保存图像的边界信息，能够有效地消除异常值的影响，对处理脉冲噪音等非高斯的加性噪音特别有效，在医学图像和计算机视觉等研究领域有广泛而成功的应用.然而，Nikolova[3]从统计的角度指出，广泛使用的TVL1模型会偏离数据获取模型和先验模型，特别是对高水平噪音.为克服这个问题，Cai等[4]提出了两阶段方法，第1阶段探索损坏的像素，第2阶段使用剩下没有被污染的像素恢复图像.数值实验表明两阶段方法优于TVL1模型，特别是对于90%的椒盐噪音和55%的随机噪音.然而，两阶段方法仍然不能有效解决高水平的随机噪音.

本文针对高脉冲噪音图像恢复开展研究，主要贡献有两个：一是提出了TVMCP模型用于高脉冲噪音图像的恢复，二是构造了近似逼近方法，从理论上证明了该方法收敛到TVMCP模型的稳定点.仿真实验验证了本文所提出模型和方法的有效性，结果显示，对于被在高水平下随机值噪音或椒盐噪音污染的图像，TVMCP方法都能取得比TVL1模型和两阶段方法更好的恢复效果.

1 TVL1模型

5 仿真实验

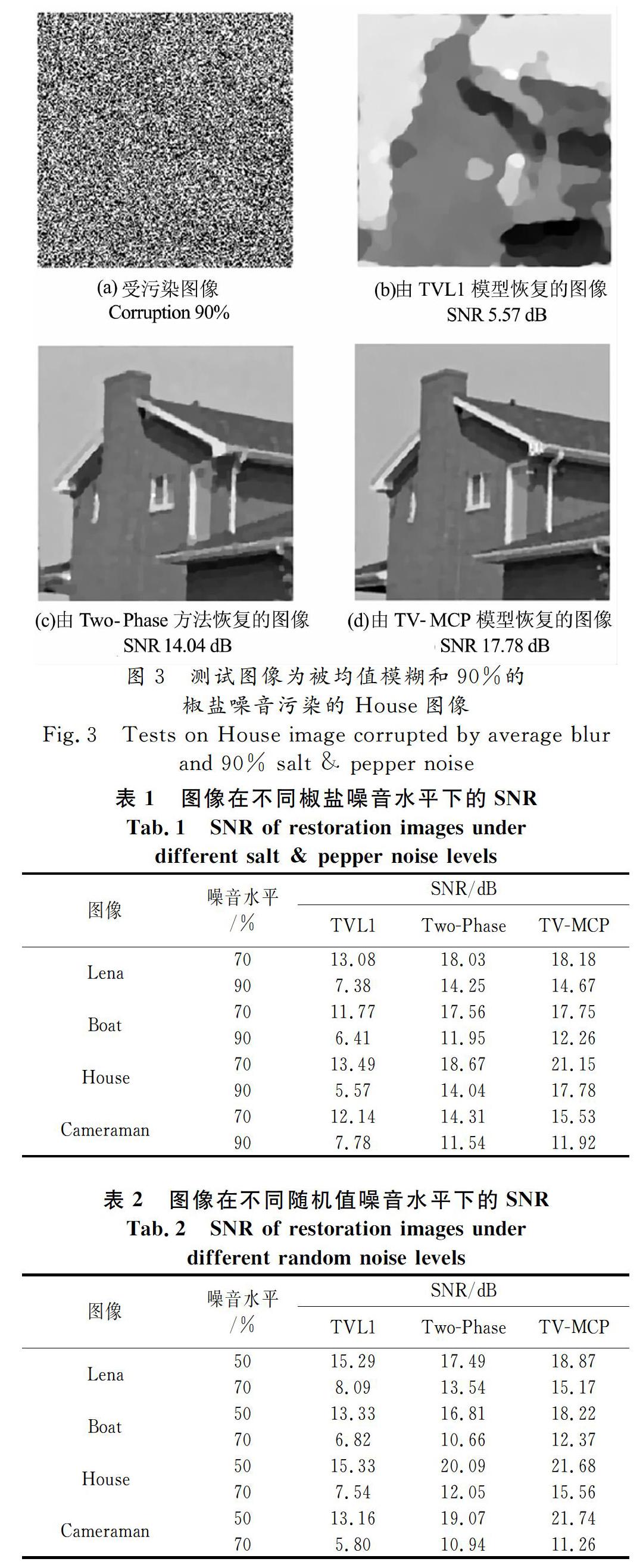
本节针对带模糊的高脉冲噪音图像的恢复问题，对TVMCP模型进行仿真实验，同时与TVL1模型和两阶段方法（Twophase）进行对比仿真实验.测试的图像包括Lena、House、Boat和Cameraman（大小均为512×512）.而模糊算子则采用9×9的均值模糊.TVL1和TVMCP模型均采用ADMM算法求解，并给出仿真结果，所有实验都是在1.6 GHz Intel Core i5 的CPU及8 G内存的OS X系统下的MacBook Air笔记本中运行MATLAB R2016b计算得出.我们采用信噪比（SNR）来评估图像恢复的效果.

在參数选取上，基于实验，（βω，βz）=（5，20）.在处理椒盐噪音污染图像时（γ1，γ2）=（1，0.15），处理随机值噪音污染的图像时（γ1，γ2）=（13.5，0.35）.

图1展示的是Lena图像和House图像的原图；图2展示的是受到70%的随机值噪音水平污染的Lena图像，用TVL1模型、TwoPhase方法和TVMCP模型的视觉恢复效果对比；图3表示House在90%的随机值噪音水平下用TVL1模型、TwoPhase方法和TVMCP模型的视觉恢复效果对比.从SNR值和视觉恢复效果对比中，可以发现本文提出的TVMCP模型能得到更好的恢复效果.

6 结 论

针对高脉冲噪音图像恢复问题，本文提出了TVMCP模型，并给出了求解TVMCP模型的ADMM算法，从理论上证明了该算法的收敛性.仿真实验的结果验证了TVMCP模型的有效性，结果表明，TVMCP模型明显优于TVL1模型和两阶段方法，能够获得更好的恢复图像，尤其是在高噪音污染的图像恢复问题上.能否将该模型和算法推广到其他噪音污染下的图像恢复问题？这个问题值得进一步研究.

参考文献

[1] CHAN T F， ESEDOGLU S. Aspects of total variation regularized L1 function approximation[J]. SIAM Journal on Applied Mathematics， 2005， 65（5）：1817-1837.

[2] YANG J， ZHANG Y， YIN W. An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise[J]. SIAM Journal on Scientific Computing， 2009， 31（4）：2842-2865.

[3] NIKOLOVA M. Model distortions in Bayesian MAP reconstruction[J]. Inverse Problems and Imaging， 2007， 1（2）：399-422.

[4] CAI J F， CHAN R H， NIKOLOVA M. Twophase approach for deblurring images corrupted by impulse plus Gaussian noise[J]. Inverse Problems & Imaging， 2008， 2（2）：187-204.

[5] ZHANG C H. Nearly unbiased variable selection under minimax concave penalty[J]. Annals of Statistics， 2010， 38（2）：894-942.

[6] GASSO G， RAKOTOMAMONJY A， CANU S. Recovering sparse signals with a certain family of nonconvex penalties and DC programming[J]. IEEE Transactions on Signal Processing， 2009， 57（12）：4686-4698.

[7] ATTOUCH H， BOLTE J， SVAITER B F. Convergence of descent methods for semialgebraic and tame problems： Proximal algorithms， forwardbackward splitting， and regularized GaussSeidel methods[J]. Mathematical Programming， 2013， 137（1）：91-129.

[8] LI G， PONG T K. Calculus of the exponent of KurdykaLojasiewicz inequality and its applications to linear convergence of firstorder methods[J]. Foundations of Computational Mathematics， 2018（online）： 1-34.