风电塔筒爬壁机器人吸附结构设计分析*

侯嘉瑞，万 熠*，孙立新

(1.山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，山东 济南 250061;2.河北工业大学 机械工程学院，天津 300132)

0 引 言

目前，风力发电已在世界各地广为应用。作为风能收集的载体—风电塔筒而言，由于制造、装配等过程存在的问题，以及长时间使用后塔筒疲劳，容易出现塔筒裂纹、表面锈蚀等状况，不及时实施对应的检修措施将会引发塔筒坍毁的严重事故[1-2]。

目前常见的人工检修法存在诸多弊端：(1)检修人员需要携带大量工具从高度极高的塔筒内攀爬到顶部；(2)检修人员悬吊在塔筒外壁工作时，由于高空风力较大，极易出现晃动，威胁检修人员的安全；(3)由于塔筒外表面面积较大，人工检修的方式容易出现漏检的情况，对于一些裂缝、锈蚀得不到完全检修，存在后续的安全隐患[3-4]。

针对上述问题，本文将设计一种能够替代人力进行风电塔筒检修的辅助工具。

1 爬壁机器人结构方案设计

1.1 整体方案布局

设计风电塔筒爬壁机器人目的是为了能替代人工进行对风电塔筒的检修，因此要求爬壁机器人能够安装不同检修装置，并通过在工作表面进行运动，完成检修任务。

综合现有研究成果及生产需求[5-6]，要求爬壁机器人能够达到的基本技术指标如表1所示。

表1 爬壁机器人性能指标

同时，考虑应用场景，该爬壁机器人应由以下功能部分组成，其主要功能分解图如图1所示。

图1 爬壁机器人主要功能分解图

常见爬壁机器人吸附方式分为：负压吸附、真空吸附、以及磁吸附[7]，以上3种吸附方式优缺点如表2所示[8]。

表2 常见爬壁机器人吸附方式

根据爬壁机器人应用场景，磁吸附结构对于运动表面的材料要求较高，需要为能被吸附的磁性材料；同时这种方式设计简单，相对其他吸附方式而言吸附力明显较大，对运动面形状要求不高。

磁吸附包括永磁体和电磁体两种吸附方式，前者结构简单、可靠性高。使用永磁吸附的设备，不会因断电等意外情况出现吸附力的消失，导致设备从工作面坠落[9]，因此设计采用永磁吸附方式。

考虑风电塔筒塔筒曲率半径不断变化的特点，以及需要较大的吸附力等因素，爬壁机器人采用履带式行走方式，通过两台驱动电机驱动状态的不同，实现爬壁机器人直线及转弯运动[10-11]。

1.2 旋转吸附机构模型的建立

由于风电塔筒外壁面曲率是变化的，不同高度直径不同，常见风电塔筒高约80 m，塔筒整体呈锥形，最窄端口直径2 800 mm，最宽端口直径3 500 mm，若考虑爬壁机器人最大设计尺寸，采用双铰链旋转结构[12]，则极端爬行位置沿塔筒切线方向贴合偏移约7.24°。根据风电塔筒高度、直径等参数计算，可得到爬壁机器人沿塔筒轴线方向贴合偏移约0.2°，该方向偏移可忽略不计。

因此，沿塔筒切线方向，爬壁机器人需要具备在一定范围内实现吸附半径变化的能力。考虑机器人在塔筒外壁转弯时，存在前端吸附结构翘起，并远离塔筒的情况，应减小吸附机构与塔筒的距离变化，要求机器人吸附结构具备旋转自由度。

根据以上分析结果，爬壁机器人需要具备两个旋转自由度。旋转吸附机构模型如图2所示。

图2 两自由度旋转吸附机构模型

2 爬壁机器人吸附状态受力分析

本文主要设计爬壁机器人吸附机构，因此在进行受力分析时主要进行静力学分析，从吸附结构的稳定吸附方面进行分析。在静止吸附状态下，造成爬壁机器人失稳的方式主要包括滑移下落、纵向翻转以及横向翻转[13]。

2.1 滑移下落

假设爬壁机器人静止，且吸附力是均匀的，则爬壁机器人静力学受力分析如图3所示。

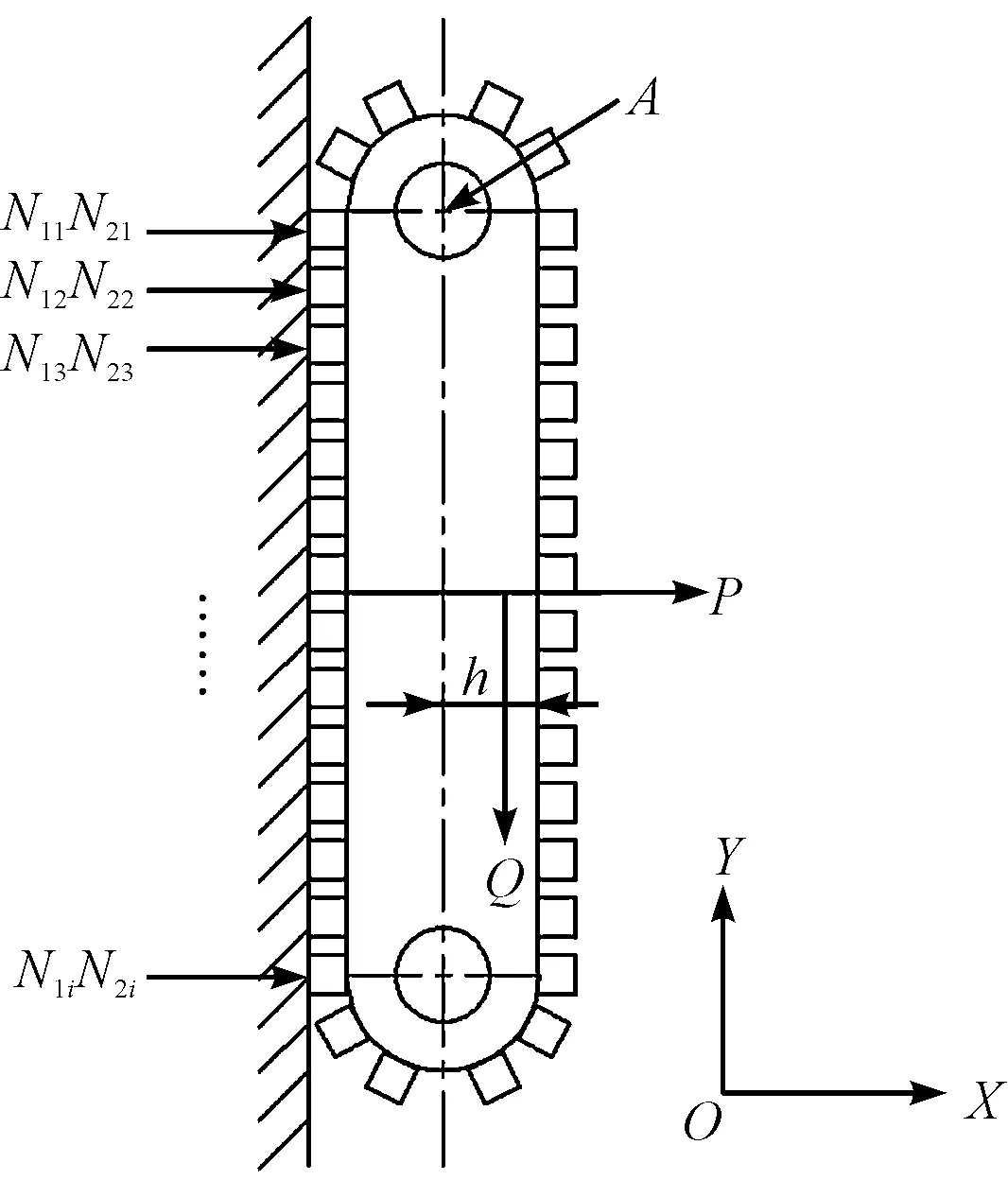
图3 爬壁机器人纵向吸附受力分析图N1iN2i-两条履带各永磁体与壁面作用力;P-永磁吸附装置在墙壁上提供的吸力;Q-爬壁机器人总重;h-爬壁机器人重力偏移轴线距离;A-爬壁机器人纵向翻转极限点

则根据受力分析可得：

(1)

(2)

F1i≤f静·N1i

(3)

F2i≤f静·N2i

(4)

式中：n—单条履带与壁面同时吸附的永磁体数量；f静—静摩擦系数。

假设各永磁体吸附力均相同，则可令：

N11=N12=…=N1i=N1

(5)

N21=N22=…=N2i=N2

(6)

由公式(1～4)可得出：

nN1·f静+nN2·f静≥Q

(7)

且N1=N2，则可得：

2nN1·f静≥Q2i

(8)

式中：N1—滑移失稳极限状态下单个永磁体吸附力。

得到结果：

(9)

2.2 纵向倾覆

爬壁机器人本体不发生纵向倾覆(即爬壁机器人在纵向静止吸附状态下不脱离墙壁)的条件为：∑MA≥0(各参数如图3所示)，通过计算可得：

2×(N×0+N×p′+N×2p′+
…+N×n-1p′)-Q·L≥0

(10)

(11)

(12)

式中：N2—纵向倾覆失稳极限状态下单个永磁体吸附力。

2.3 横向倾覆

爬壁机器人本体不发生横向倾覆(即爬壁机器人在横向静止吸附状态下，不会出现脱离墙壁的情况)的条件为：∑MB≥0。

受力分析如图4所示。

图4 爬壁机器人横向吸附受力分析图N1iN2i-单条履带各永磁体与壁面作用力;b-爬壁机器人两履带吸附中心距离;B-爬壁机器人横向翻转极限点

根据图4参数可得：

n×N×0+n×N×B-Q·L≥0

(13)

n·N·B-Q·L≥0

(14)

(15)

式中：N3—横向倾覆失稳极限状态下单个永磁体吸附力。

2.4 静止吸附状态失稳极值计算

根据以上爬壁机器人常见失稳状态分析，考虑安全系数，爬壁机器人所需最大吸附力为：

(16)

式中：K—安全系数。

根据设计参数可得：Q=400 N,L=60 mm,p′=33 mm,n=11,B=30,f静=0.4,K=1.5。将参数代入式(16)可得：N≥68.18 N。

可见，要实现爬壁机器人的稳定吸附，其与壁面贴合吸附的每个吸附单元所需提供的吸附力N≥68.18 N。

3 永磁吸附结构设计与仿真分析

3.1 方案设计

根据上述分析计算可知，每个吸附单元应具备至少“68.18 N”的吸附力，同时考虑吸附单元外部需要嵌套防磨橡胶，因此设备吸附单元选用稀土永磁材料钕铁硼(Nd-Fe-B)，这种永磁材料磁能积较大，现已在相关领域得到了的广泛应用[14]。

永磁体单元的布置主要有：“单块永磁体与两块分离永磁体”、“有无扼铁”等方式。本文经过试验仿真得出，选用两块分离永磁体，添加扼铁的方案产生的相对吸附力最大。

吸附方案如图5所示。

3.2 磁力仿真

常见风电塔筒的壁厚约为15 mm，同时本研究根据传动部分设计结果，及计算得到的永磁体吸附力，初步确定单块永磁体尺寸为8 mm×22 mm×30 mm。由此可通过Maxwell软件进行磁铁吸附力的仿真。

图5 吸附单元方案1-橡胶隔套；2-隔磁体；3-永磁体；4-轭铁

令永磁体距壁面的距离、轭铁的厚度为变量，本研究观察不同参数下吸附力的变化情况(仿真采用2D模型，数据中对壁面产生吸附力为永磁体厚度为30 mm时，不同参数变化产生的吸附力大小)。

综合分析曲线如图6所示。

图6 吸附力综合分析曲线

4 实验及结果分析

根据综合分析曲线结果以及制造难易程度，可得到相对最优目标点：即当永磁体距壁面距离为3 mm，轭铁厚度为2.5 mm时，所求永磁体吸附力仿真结果为70.42 N。此结果最接近计算结果68.18 N。此时的吸附单元的磁力仿真如图7所示。

图7 设计仿真结果分析图

实验结果表明：在该实际应用条件下，爬壁机器人吸附能力符合稳定吸附要求，说明该爬壁机器人结构可以稳定吸附于风电塔筒外壁面。

根据吸附单元仿真结果，结合吸附单元结构设计方案及整机设计方案，最终可得到一种适用于风电塔筒外壁检修的爬壁机器人三维模型，如图8所示。

图8 爬壁机器人结构三维模型

通过在该机器人上安装不同工具，操作人员即可完成对风电塔筒的检测、清理、修复等任务。

5 结束语

针对风电塔筒的检修工作，通过对爬壁机器人的结构设计分析，本文借助Solidworks、Maxwell等软件，设计了一种双旋转自由度的爬壁机器人结构：

(1)该结构灵活度高，通过双旋转自由度可使吸附单元自主贴合风电塔筒外壁轮廓，保证机器人吸附爬行的稳定性；

(2)进行了爬壁机器人静止状态下的受力分析，考虑不同情况下的失稳边界条件，根据给定参数计算得到吸附单元相对最优吸附力N≥68.18 N，并在确定吸附单元构型后进行磁力仿真，得到实际情况下吸附力N=70.42 N；

(3)仿真结果表明：采用该吸附单元的爬壁机器人结构，可以稳定吸附于风电塔筒外壁面。