基于缺口疲劳理论的曲轴结构疲劳特性研究*
李建锋,钟剑锋,刘震涛*
(1.潍柴动力股份有限公司 内燃机可靠性国家重点实验室,山东 潍坊 261061;2.浙江大学 动力机械及车辆工程研究所,浙江 杭州 310027)
0 引 言
对于曲轴等工作环境较为恶劣的发动机零部件而言,疲劳极限载荷是其重要的性能参数之一。传统工程当中,该参数往往通过对曲轴进行标准疲劳试验获取。该方法能够对曲轴的疲劳特性进行较为准确的评价,但成本较高,且无法在曲轴的设计阶段完成[1]。因此如何快速准确获取曲轴的疲劳极限载荷,是曲轴疲劳研究的重点问题[2]。
针对该类问题,近年来国内外学者做了大量的研究工作。其中,TAYLOR[3-6]提出了裂纹模拟技术,通过构造与构件应力梯度一致的标准裂纹体,对同样材料属性、不同结构的曲轴的疲劳极限载荷进行预测,但是由于二者之间应力状态的本质差异,预测结果有时会导致较大的误差;针对这一不足,陈晓平[7]提出了利用等效缺口件预测曲轴的疲劳极限载荷的方法,取得了更准确的预测结果;陈渊博、郑康[8-9]采用多体动力学计算了曲轴和轴承座在循环工况内的复合载荷作用下的疲劳寿命,取得了更具指导意义的结论。
在实际工程当中,相比较曲轴这样的发动机零部件,一些缺口件的疲劳极限载荷预测已经有了较为成熟的方法。相关研究者提出了相应的经验公式,可以对缺口件的疲劳强度进行准确预测[10]。另一方面,曲轴在弯矩载荷作用下时,疲劳失效发生在应力集中的曲柄销圆角区域,这一现象与缺口件疲劳失效过程相类似。同时在曲轴发生疲劳失效的圆角部位,也有类似于三维缺口件的缺口的变截面结构。
基于该宏观现象,本研究中尝试将曲轴作缺口件处理,并利用现有的缺口件疲劳极限载荷预测模型,对曲轴的疲劳极限载荷进行预测研究。
1 曲轴缺口疲劳模型
疲劳缺口系数反映了缺口对缺口件疲劳强度的影响,被认为是能够准确预测缺口件疲劳强度的参数之一,其具体的定义形式为[11]:
(1)
式中:Se,SN—标准光滑试件与缺口件的疲劳强度。
而在实际工作过程中,缺口件因为其缺口部位的结构特性,往往会存在应力集中现象,其真实的疲劳强度为:
(2)
式中:Kt—缺口件的应力集中系数;σmax,σn—构件在外载作用下的真实应力和名义应力。
目前,针对疲劳缺口系数,国内外学者进行了大量的研究,并提出了相应的预测模型。对于这些疲劳缺口系数模型,当它们在实际工程中的研究对象不同时,其适用性和预测精确度也会有所不同。对于曲轴而言,其在实际工程当中的疲劳失效问题一般都是属于高周疲劳。相关的预测模型中,Peterson模型被认为是能够准确预测构件高周疲劳强度的模型之一[12],并得到广泛应用,其表达形式为:
(3)
式中:ρ—缺口件的缺口半径,参照曲轴的结构特点,可以认为当利用该方法对曲轴的疲劳特性进行研究时,该参数就是曲轴的圆角半径;a—材料特征长度,一般被认为是只与材料属性有关的常数。
该模型由Peterson提出,认为对于任意结构形式的缺口件,当它在外载作用下时,应力从缺口根部向内线性减小。同时考虑应力相对较低的材料对高应力材料的支撑效应,认为缺口根部长度一定范围内的平均应力等于或大于光滑试件疲劳强度时,缺口件就发生疲劳破坏现象。该模型因为其表达形式比较简单,在实际工程中得到了广泛应用。本文基于该模型,对曲轴的疲劳极限载荷进行预测研究。
2 曲轴疲劳极限载荷预测方法
2.1 曲轴应力集中系数计算方法
由Peterson模型的定义可知,构件的疲劳缺口系数可以由其应力集中系数计算获取。其中,σmax可以由曲轴有限元模型计算获取,σn是构件弯矩与抗弯截面的商,因此抗弯截面的准确获取是应力集中系数、疲劳缺口系数计算的基础。
目前,曲轴的抗弯截面主要存在3种定义方式。其中高镇同[13]认为曲轴在受到弯矩载荷作用时,其抗弯截面就是曲轴的曲柄销的圆截面,如图1所示。

图1 曲轴抗弯截面第一定义
当基于该方法定义曲轴的抗弯截面时,其抗弯截面是规则圆截面。由材料力学相关理论可知,该截面在受到弯矩作用时,其抗弯模量I为:
(4)
式中:d—曲轴曲柄销的直径。
而在实际工程当中,曲轴在受到交变弯矩载荷作用时,裂纹通常是由曲柄销圆角处萌生,沿着曲柄销圆角至主轴颈圆角方向扩展,因此Ricardo公司认为该裂纹扩展面即为曲轴的抗弯截面[14],如图2所示。

图2 曲轴抗弯截面第二定义
当基于该方法定义曲轴的抗弯截面时,该截面并非规则截面,因此相应的抗弯模量I2无法直接利用公式计算获取,可以利用三维CAD软件读取截面参数。而AVL公司认为,曲轴的抗弯截面为该截面的水平投影,该截面的截面模量为:
I3=I2cos2α
(5)
式中:I3—基于抗弯截面第三定义的抗弯截面模量;I2—基于抗弯截面第二定义的抗弯截面模量;α—曲轴的裂纹扩展面与水平线之间的夹角。
2.2 曲轴疲劳极限载荷预测方法
目前,在实际工程当中,这3种定义方法都得到了一定的应用。本文分别基于这3种定义方式,通过对某批次曲轴在极限载荷作用下的应力状态进行分析,在此基础上计算相应的Peterson模型中参数a值,并对结构不同、材料属性相同的曲轴的疲劳极限载荷进行预测,具体方法为:
(1)利用有限元法对某批次曲轴在弯矩载荷作用下的应力状态进行分析,载荷大小为该款曲轴的标定载荷,并利用最小二乘法对计算结果和标定的圆角应力值进行拟合,获取曲轴在该载荷下的真实应力值σrmax1;
(2)对比曲轴在疲劳极限载荷作用下的真实应力值σrmax、名义应力值σnom1以及材料的疲劳强度,就可以获取该曲轴的疲劳缺口系数值,并在此基础上利用公式(2,3)推算得到Peterson模型参数a值;
(3)对另外一款结构不同、材料属性一致的曲轴施加的1 000 N·m的弯矩载荷,利用有限元法对该曲轴的应力集中系数进行计算,并结合已知的Peterson模型参数对其疲劳缺口系数进行计算,在此基础上预测该曲轴的疲劳极限载荷,预测结果为:
(6)
3 曲轴算例
3.1 曲轴算例一
本研究建立曲轴的简化模型,如图3所示。

图3 曲轴简化有限元模型
基于上述方法,本研究选择编号为No.0的某款曲轴,对其进行仿真计算和试验结果的对比分析,结果如表1所示。

表1 No.0曲轴圆角最大主应力应力值对比
表1中数据表明:当利用有限元法对曲轴的圆角应力进行仿真计算时,计算结果与实际的应力测量值之间存在一定的误差,但相应的误差范围都控制在10%之内,这对于一般工程应用来说,已经可以满足精度方面的要求。利用最小二乘法对二者之间的关系进行拟合,则有:
σr=0.973σFE-1.8
(7)
式中:σr—曲轴的真实应力值;σFE—有限元法获得的应力值。
将有限元计算的相关结果代入式中,可得曲轴在其极限弯矩载荷作用下的真实应力值为475 MPa。分别基于不同的抗弯截面定义方法对No.0曲轴在极限载荷作用下的名义应力进行计算,相应的结果如表2所示。

表2 No.0曲轴基于不同抗弯截面定义的名义应力(极限载荷作用下)
该算例中,曲轴材料为42CrMo,其疲劳强度为386 MPa,同时No.0曲轴的曲柄销圆角半径为5 mm,对比该参数以及No.0曲轴在其极限载荷下的名义应力值,就可以得到该曲轴基于不同抗弯截面定义方法的应力集中系数及疲劳缺口系数(计算公式见式(2,3)),并对Peterson模型参数a进行推算,结果如表3所示。

表3 Peterson模型参数a计算结果(基于不同抗弯截面定义方法)
对与No.0曲轴材料属性一致,但是结构不同的No.1曲轴施加大小为1 000 N·m的弯矩载荷,本研究利用有限元法计算该曲轴在该载荷下的最大主应力值,结果为234 MPa。基于不同的抗弯截面定义方法计算该曲轴的名义应力值及应力集中系数,相应的计算结果如表4所示。

表4 No.1曲轴基于不同抗弯截面定义的名义应力(1 000 N·m载荷作用下)
本研究中,No.1曲轴的圆角半径为3 mm,代入该参数及曲轴在不同抗弯截面定义方式下的应力集中系数,就可以推算得到相应的疲劳缺口系数及极限名义应力值,结果如表5所示。
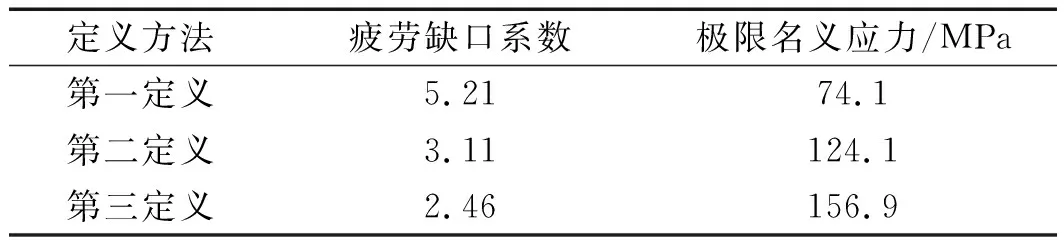
表5 No.1曲轴极限名义应力计算结果(基于不同抗弯截面定义)
对比该极限名义应力值和表4中曲轴在1 000 N·m弯矩载荷作用下的名义应力,可得基于不同的抗弯截面定义方式的疲劳极限载荷为:
3.2 曲轴算例二
基于同样的方法,笔者选择另外一组曲轴作为研究的对象,其疲劳极限载荷的中值为5 292 N·m。该批次的曲轴的编号为C0,相应的圆角应力标定结果如表6所示。

表6 C0曲轴圆角最大主应力应力值对比
利用最小二乘法对二者之间的关系进行拟合,则有:
σr=1.012σFE+9.7
(8)
笔者将有限元计算的相关结果代入式中,可得曲轴在其极限弯矩载荷作用下的真实应力值为475 MPa。笔者分别基于不同的抗弯截面定义方法对C0曲轴在极限载荷作用下的名义应力进行计算,该算例中,C0曲轴材料的疲劳强度为396 MP,其曲柄销圆角半径值为5 mm,对该曲轴的应力集中系数、疲劳缺口系数以及Peterson模型参数进行推断。在完成上述分析的基础上,与算例1类似,对与C0曲轴材料属性一致,但是结构不同的C1曲轴施加大小为1 000 N·m的弯矩载荷,利用有限元法计算该曲轴在该载荷下的最大主应力值,结果为234 MPa。基于不同的抗弯截面定义方法计算该曲轴的名义应力值及应力集中系数,相应的计算结果如表7所示。

表7 C1曲轴基于不同抗弯截面定义的名义应力(1 000 N·m载荷作用下)
本研究中,C1曲轴的圆角半径为3 mm,代入该参数及曲轴在不同抗弯截面定义方式下的应力集中系数,结果如表8所示。

表8 C1曲轴极限名义应力计算结果(基于不同抗弯截面定义)
对比该极限名义应力值和表8中C1曲轴在1 000 N·m弯矩载荷作用下的名义应力,可得基于不同的抗弯截面定义方式的疲劳极限载荷为:
4 疲劳试验验证
本研究采用机械谐振式曲轴弯曲疲劳试验装置对这两款曲轴进行弯曲疲劳试验。试验过程中载荷的控制以及失效判定参照文献[15-16]。这两种曲轴的疲劳试验数据如表(9,10)所示[17]。
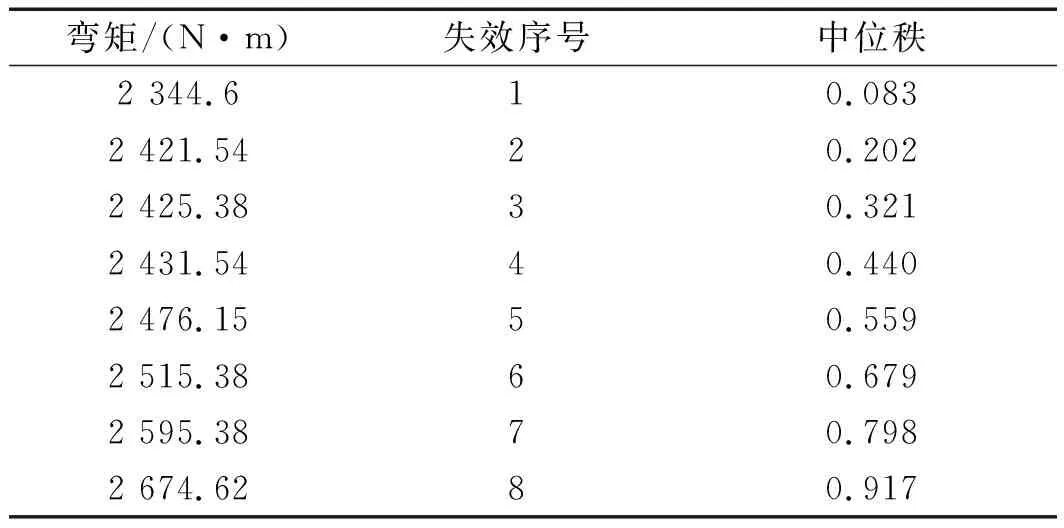
表9 No.1曲轴疲劳极限中位秩(失效概率)估计

表10 C1曲轴疲劳极限中位秩(失效概率)估计
文献[18]研究了构件疲劳极限载荷的分布规律,提出可以利用正态分布函数统计曲轴的疲劳极限载荷。采用该方法,对No.1与C1曲轴的疲劳极限载荷进行分析,可得这两款曲轴的疲劳极限载荷分别为2 481 N·m与2 565 N·m,相应的误差如表11所示。
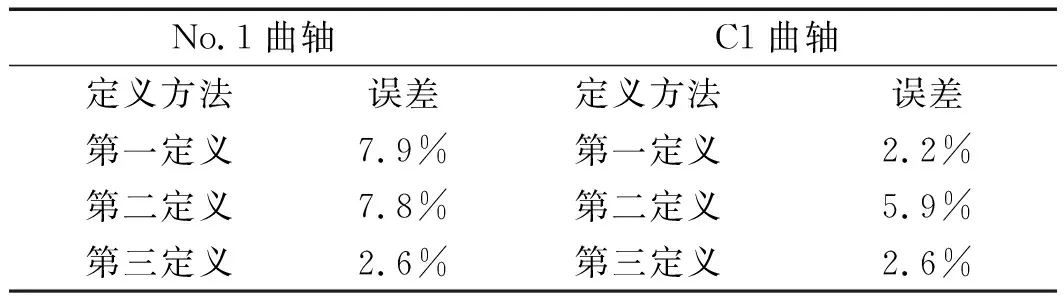
表11 No.1&C1曲轴疲劳极限载荷预测误差
由表11可以看出:在基于不同抗弯截面定义及疲劳缺口系数理论对这两款材料属性相同、曲拐结构不同的曲轴的疲劳极限载荷进行预测时,所有预测结果的误差都控制在10%之内,其中基于第三定义的结果误差最小,这样的精度已经可以满足一般实际工程的需求。
5 结束语
基于缺口疲劳理论,本研究对曲轴的疲劳极限载荷进行了预测,并利用标定数据对曲轴的圆角应力进行了修正,结合曲轴自身的结构特性推算得到了相应的Peterson模型参数。
基于3种不同的抗弯截面定义方法,本研究对曲轴的应力集中系数的计算以及疲劳极限载荷的预测方法进行了系统研究。在上述研究的基础上对两款同种材料、不同结构的曲轴的疲劳极限载荷分别进行预测,通过与试验数据对比分析发现预测结果具有一定的精度,3种不同定义方法的最大误差都小于10%,其中基于第3种抗弯截面定义方法的预测误差最小(最大误差≤2.6%),说明对于曲轴疲劳极限载荷预测,该方法具有更高的工程适用性。

