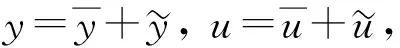一类耦合含梯度项的退化抛物方程组的近似可控性
杜 润 梅
(长春工业大学 基础科学学院, 长春 130012)
考虑如下耦合系统:
其中:QT=Ω×(0,T),Ω是n中的非空有界区域, 其边界∂Ω分片光滑,T>0;h∈L2(QT);χ是特征函数;ω是Ω中的非空开子集;bj,cj∈L∞(QT),j=1,2;y0,u0∈L2(Ω); 函数满足条件a(x,t)>0, (x,t)∈QT,Σ定义为
由于a(x,t)可能在Ω的边界处为零, 因此方程组(1)-(2)是边界退化的抛物方程组[1-2]. 目前, 关于退化抛物方程可控性的研究已有很多结果: 文献[3-6]研究了如下退化抛物方程:
其中b,c∈L∞(QT), 在相应的初边值条件下, 证明了该系统的近似可控性; 文献[7]研究了当b1=b2=0时, 耦合系统(1)-(4) 的近似可控性. 本文利用文献[7]的方法, 通过对共轭系统的研究, 证明问题(1)-(4)的近似可控性. 即证明对任意允许误差ε>0和任意给定的(yd,ud)∈L2(Ω)×L2(Ω), 存在控制函数h, 使得问题(1)-(4)的解(y,u)在时刻T处可近似达到(yd,ud), 即
(5)
定义1如果对任意满足φt,ψt∈L2(QT)和φ(·,T)|Ω=ψ(·,T)|Ω=0的φ,ψ∈C([0,T];L2(Ω))∩B, 有
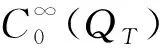
类似文献[3]中引理2.1, 可以证明系统(1)-(4)的适定性:
定理1系统(1)-(4)存在唯一弱解(y,u), 且满足
其中C>0是一个仅依赖于Ω,T,‖b1‖L∞(QT),‖b2‖L∞(QT)‖c1‖L∞(QT),‖c2‖L∞(QT)的常数.
考虑系统(1)-(4)的共轭系统:
定义映射

命题1共轭系统(6)-(9)具有唯一延拓性, 即若z在Qω上几乎处处为0, 则z和v在QT上几乎处处为0.
证明: 由方程(6)及z在Qω上几乎处处为0, 可知v在Qω上几乎处处为 0. 对充分小的δ>0, 记Ωδ={x∈Ω: dist(x,∂Ω)>δ}. 在Ωδ×(0,T)上, 方程(6),(7)是非退化的. 由一致抛物方程的唯一延拓性[8]可知,u和v在Ωδ×(0,T)上几乎处处为 0. 再由δ的任意性可知,u和v在QT上几乎处处为0. 证毕.
对于(z0,v0)∈L2(Ω)×L2(Ω), 定义泛函
类似文献[7]中命题2.2, 可得如下结论.
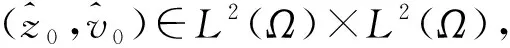
定理2当(y0,u0)=(0,0)时, 系统(1)-(4)是近似可控的, 即对任意给定的yd,ud∈L2(Ω)和ε>0, 存在函数h∈L2(QT), 使得系统(1)-(4)的解(y,u)满足式(5).
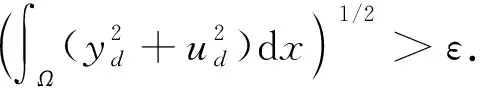
(10)
由(y,u)是系统(1)-(4)的弱解可知,
由(θ,ψ)是系统(6)-(9)当(z0,v0)=(θ0,ψ0)时的解可知,
由式(11)-(14), 可得
(15)
由(θ0,ψ0)的任意性可知式(5)成立. 证毕.
定理3对任意的(y0,u0)∈L2(Ω)×L2(Ω), 系统(1)-(4)是近似可控的.
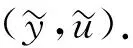
(16)