基于最小生成树的多层次k-Means聚类算法及其在数据挖掘中的应用

金晓民, 张丽萍

(1. 内蒙古大学 交通学院, 呼和浩特 010021;2. 内蒙古自治区桥梁检测与维修加固工程技术研究中心, 呼和浩特 010070;3. 内蒙古师范大学 计算机科学技术学院, 呼和浩特 010022)

数据挖掘就是从大量随机的、 模糊的、 有噪声的、 不完全的数据中, 提取潜在的、 未知的、 隐含的、 有应用价值的模式或信息的过程[1-3]. 数据挖掘中重要的步骤是聚类[4], 聚类将数据分为多个簇或类, 使相似度较高的对象在一个类中, 不同类别中的数据相似度较低[5]. 对稀疏和密集区域的识别通过聚类完成, 并通过聚类发现数据属性和分布模式间存在的关系[6]. 数据聚类广泛应用于医疗图像自动检测、 客户分类、 卫星照片分析、 基因识别、 空间数据处理和文本分类等领域[7].

在低维情况下, 数据挖掘方法通过人眼进行模式识别及SOM(self organizing maps)可视化功能确定聚类的数目, 完成数据的挖掘, 该方法存在挖掘时间长和挖掘结果不准确的问题[8]. Means算法是数据聚类分析中常用的划分方法, 以准则函数和误差平方作为数据聚类的准则, 可快速、 有效地完成大数据集的处理. MFA算法是一个优先考虑边权值进行社团划分的算法, 同时也继承了通过优化Q值进行社团划分的特点. 文献[9]提出了一种基于改进并行协同过滤算法的大数据挖掘方法, 通过分析协同过滤算法的执行流程, 针对传统协同过滤算法的不足, 从生成节点评分向量、 获取相邻节点、 形成推荐信息等方面对传统协同过滤算法进行改进, 得到了从运行时间、 加速率和推荐精度三方面均运行效率较高的改进并行协同过滤算法.k-means算法依赖于数据输入的顺序和初始值的选择, 通过准则函数和误差平方对聚类效果进行测度, 各类的大小和形状差别较大[10]. 为了优化挖掘过程, 本文提出一种基于最小生成树的多层次k-means聚类算法对数据进行挖掘.

1 数据类型与聚类准则函数设计

1.1 聚类分析中的矩阵类型选取

1) 数据矩阵. 数据矩阵表示一个对象的属性结果, 是数据之间的关系表, 每列都表示对象的一类属性, 每行表示数据对象, 如通过m个属性对数据对象进行描述, 属性一般为种类、 高度等.n个对象中存在m个属性可通过n×m矩阵表示为

(1)

2) 差异矩阵. 数据对象之间的差异性用差异矩阵进行储存, 差异矩阵用n×n维矩阵表示, 其中d(i,j)为差异矩阵中的元素, 表示数据对象i和j之间存在的差异程度, 表达式为

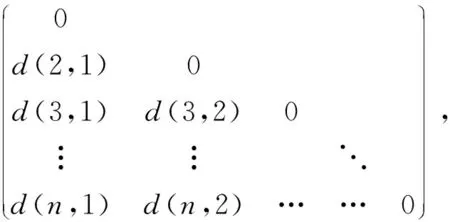
(2)

差异矩阵中的元素d(i,j)≥0, 数据对象间的相似度越高, 该数据越接近于0； 数据对象之间的相似度越低, 该数据越大.

1.2 聚类准则和加权平均平方距离计算函数设计

1) 误差平方和准则函数设计. 设X={x1,x2,…,xn}表示混合样本集, 通过相似性度量将混合样本集聚类成C个子集X1,X2,…,XC, 每个子集都表示一个数据的类型, 分别存在n1,n2,…,nC种样本. 采用准则函数和误差平方对数据聚类的质量进行衡量, 表达式为

(3)

其中：mj表示数据样本在类中的均值；JC表示准则函数, 是聚类中心和样本的函数,JC值越大, 表示聚类过程中存在的误差越大, 得到的聚类结果较差.

2) 加权平均平方距离计算. 数据聚类过程中的加权平均平方距离和准则的表达式为

(4)

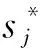
(5)

用数据的类间距离和准则Jb2及类间距离和准则Jb1对聚类结果类间存在的距离分布状态进行描述,Jb1和Jb2的计算公式为

其中：mj表示样本在数据类别中的均值向量;m表示数据样本全部的均值向量; pj表示数据类别的先验概率[11].

2 算法设计

2.1 基于最小生成树的初始中心点选取

各矩形单元中存在的数据对象个数用最小生成树分割, 计算公式为

(8)

其中：RecU表示矩形单元;DataN表示样本数据的总数; SF表示细分因子; k表示聚类数. 最小生成树分割得到的矩形单元均值计算公式为

(9)

其中: S表示数据对象在矩形单元中的线性和; W表示矩形单元权重. 数据对象在各矩形单元中密集程度的计算公式为

(10)

其中： vi表示每个矩形单元的面积; ni表示数据对象在每个矩形单元中的数量; dmin和dmax分别表示矩阵单元中最小数据和最大数据的距离值.

用最小生成树对样本数据X={x1,x2,…,xn}进行划分,CenterRecU表示分割后得到的矩形单元RecU, 其反映了样本数据集的分布状况. 采用数据集X′对集合CenterRecU进行表示, 用矩形单元密度对数据集X′进行降序排序, 初始聚类中心在数据集X′中选取, 记C={C1,C2,…,Ck}, 用矩形单元中心对数据集X′进行聚类, 得到k个类, 原始样本数据集的初始中心点通过在矩形单元中进行操作获得[12].

2.2 算法描述

设X1和X2表示样本的数据集,Dist(Ci,Cj)表示样本簇与样本簇之间的距离, 函数Dist(Ci,Cj)的表达式为

(11)

其中： Ci和Cj分别表示含有xi和xj的两个不同聚类簇； xi和xj分别表示数据集Xi和Xj中的样本点； 用欧氏距离计算函数Dist(xi,xj)中数据间的距离； n1和n2表示数据对象在两个样本簇中的个数. 平均簇间距定义为

(12)

其中, Ci和Cj表示两个不同的聚类簇. 如果AvgDist(C)大于两个簇间的距离, 则不处理这两个簇, 继续比较, 直到AvgDist(C)小于两个簇之间的距离为止. 算法步骤如下：

1) 通过k个中心点集C={C1,C2,…,Ck}构建最小生成树.

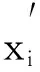
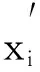
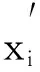
(13)

6) 用式(12)比较k个聚类簇之间的距离, 如果平均簇间距AvgDist(C)大于两个簇之间的距离, 则对两个簇进行合并, 直到平均簇间距AvgDist(C)小于两个簇之间的距离为止. 用最小生成树得到的增量数据与初始聚类中心建立最小生成树, 用最近邻搜索方法将增量数据依次划分到相应的聚类中, 完成数据的聚类, 并根据类间的平均距离对聚类结果进行完善和修正, 获得最优的聚类结果, 完成数据挖掘.

基于最小生成树的多层次k-means聚类算法流程如图1所示.

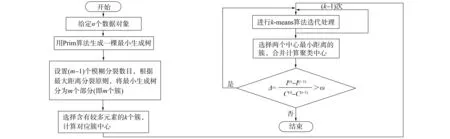
图1 多层次k-means聚类算法流程Fig.1 Flow chart of multi-level k-means clustering algorithm

3 算法应用

实验1为了验证基于最小生成树的多层次k-means聚类算法对数据挖掘的有效性, 下面对该算法进行测试, 操作系统为Windows7.0. 基于聚类结果越精准得到的数据挖掘结果越准确的原则, 分别采用基于最小生成树的多层次k-means聚类算法与传统k-means算法进行测试, 对比两种不同算法对数据挖掘过程中的聚类结果, 测试结果如图2所示, 图2中不同形状表示不同类别的数据.

由图2可见: 采用基于最小生成树的多层次k-means聚类算法对数据进行聚类时, 可准确地对不同类别的数据进行划分; 采用传统k-means算法对数据进行聚类时, 得到的分类中存在不同类别的数据, 聚类结果不准确. 因此, 基于最小生成树的多层次k-means聚类算法可准确地对数据进行挖掘.

实验2在k-means算法中, k值决定在该聚类算法中所要分配聚类簇的多少, 同时影响算法的聚类效果和迭代次数, 因此利用Canopy算法先进行粗略的聚类, 产生簇的个数为6, 即k-means算法的k=6.

图2 两种不同算法的聚类结果Fig.2 Clustering results of two different algorithms

在k=6的条件下, 为进一步验证本文算法的优越性, 在分类簇的划分过程中, 可用挖掘数据对象到簇中心的距离衡量算法的优劣. 聚类过程中, 距离计算次数能很好地衡量挖掘算法的相关性能. 通过对本文改进k-means算法和传统的MFA算法的距离计算次数进行比较, 完成性能对比, 对比结果如图3所示. 由图3可见, 本文提出的改进k-means算法得到的距离计算次数比传统MFA算法少, 随着计算挖掘控制维度的不断增加, 这种优势对比越来越明显. 与MFA算法相比, 在数据维度不断增加的集合中, 本文算法的效率提升约50%. 利用本文提出的改进k-means算法和MFA算法在运行实际效率上进行实验对比, 结果如图4所示. 由图4可见, 本文算法在每次迭代过程中, 在时间效率上都优于传统MFA算法, 且维度越大, 效果越明显.

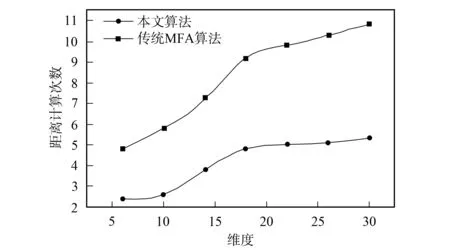
图3 不同算法的数据点距离计算数比较Fig.3 Comparison of calculation number of data points distance of different algorithms

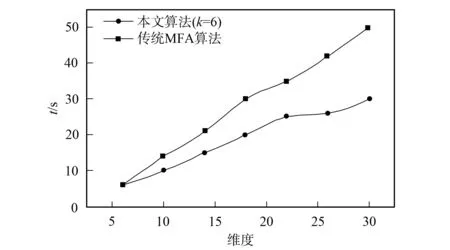
图4 不同算法迭代阶段的运行时间比较Fig.4 Comparison of running time of different algorithms in iterative stages

由以上分析可知, 当k=6时, 本文提出的算法在时间效率上优于传统的MFA挖掘算法.

图5 不同算法的效率测试结果比较Fig.5 Comparison of efficiency test results of different algorithms

实验3选择初始点和聚类迭代次数在数据挖掘中均较耗时的两个阶段, 分别采用基于最小生成树的多层次k-means聚类算法、 文献[9]算法及传统MFA算法对数据进行挖掘, 对比不同算法进行数据挖掘的效率, 结果如图5所示.

由图5可见, 采用基于最小生成树的多层次k-means聚类算法对数据进行挖掘时, 在选择初始点阶段的迭代次数较多, 在聚类阶段中的迭代次数较低. 采用其他算法对数据进行挖掘时, 在选择初始点阶段的迭代次数较少, 但在聚类阶段中的迭代次数较多. 对比基于最小生成树的多层次k-means聚类算法其他和算法的迭代次数可知, 基于最小生成树的多层次k-means聚类算法的总体迭代次数少于其他算法的总体迭代次数, 因此基于最小生成树的多层次k-means聚类算法对数据进行挖掘时迭代次数较少, 挖掘所用时间较短.

综上可见, 针对传统聚类算法挖掘数据时, 存在挖掘结果不准确、 挖掘时间长的问题, 本文提出了一种基于最小生成树的多层次k-means聚类算法, 解决了目前数据挖掘效率低的问题, 可有效提高信息检索率.