采用混合粒子群算法的四杆机构参数优化与轨迹误差研究*

王亚茹，李 静

(1.吉林工程职业学院 机电工程学院，吉林 四平 136001；2长春理工大学 机电工程学院，长春 130022)

0 引言

平面四杆机构是多杆机构中比较常见的一类机构，是复杂多杆机构研究的基础[1]。四杆机构不但能够在机器中加工各种生活产品，而且具有制造容易、结构简单、传递力大及润滑方便等优点，广泛应用于机器人、汽车、航空及农业等许多领域。在四杆机构的实际应用中，运动轨迹产生的误差是许多研究者常常遇到的问题。而多杆机构由四杆机构和几种基本杆件组合。因此，也是导致多杆机构运动轨迹产生误差的根源。

当前，已有学者对四杆机构几何参数进行优化，并对优化后的运动轨迹误差进行了仿真研究，形成了一系列理论和方法。例如：文献[2]采用了遗传算法优化四杆机构几何参数，并且对优化参数进行误差仿真，降低了四杆机构横向和纵向误差，但是采用单一的遗传算法优化的结果并非全局最优值。文献[3]采用高斯-牛顿迭代算法优化四杆机构几何参数，并且对四杆机构运动轨迹进行了仿真验证，降低了横向或纵向运动轨迹误差，但是不能同时降低横向和纵向误差。文献[4]将四杆机构角位移问题转化为从动件铰链点的坐标计算问题，为了降低求解难度，建立线性方程求解，结合VB语言进行机构的运动仿真，但是要学习复杂的编程语言，运动轨迹误差也较大。文献[5]采用修正误差函数构造运动轨迹误差，通过Matlab工具箱软件直接优化修正误差函数，得出最优几何参数并进行误差仿真，降低了四杆机构横向和纵向误差，但是选择优化的等价因数和指定的运动轨迹点比较片面。对此，本文对四杆机构几何参数引入混合粒子群算法进行优化。创建平面四杆机构连杆尺寸及运动角度模型简图，通过向量关系式求解运动轨迹点的横向和纵向方程式。分析四杆机构可变参数变量，构造运动轨迹横向和纵向误差函数，对四杆机构运动条件进行约束。采用混合粒子群算法搜索四杆机构几何参数最优值，将优化前与优化后几何参数结果输入到Matlab软件中，对四杆机构运动轨迹误差进行仿真结果对比，为深入研究多杆机构运动轨迹误差提供了理论依据。

1 四杆机构运动分析

具有四个构件(包括机架)通过低副连接组成的机构称之为四杆机构，四杆机构平面示意图，如图1所示。

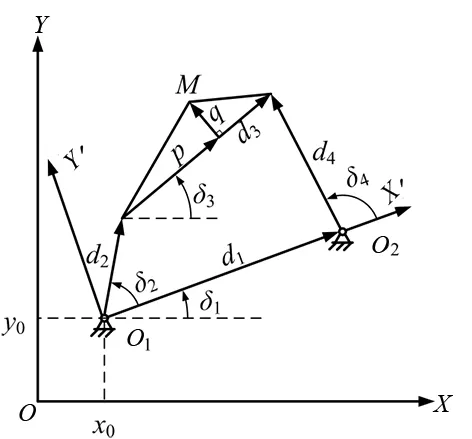
图1 四杆机构平面示意图

根据闭合矢量关系可知，四杆机构连杆尺寸满足以下方程式[3]：

d2+d3=d1+d4

(1)

式中，d1、d2、d3、d4分别表示四杆机构机架长度、主动连接杆长度、连接杆的长度及被动连接杆长度。

假设机架开始处于水平位置，则公式(1)可以转换为：

(2)

式中，δ1、δ2、δ3、δ4分别表示机架初始位置角度、主动连接杆旋转角度、连接杆运动角度及被动连接杆旋转角度。

方程组(2)的等价方程组为：

(3)

式中，L1=d1/d2，L2=d1/d4，L3=(d22-d32+d42+d12)/2d2d4，L4=d1/d3，L5=(d42-d12-d22-d32) /2d2d3。

求解方程组(3)得到δ3和δ4，其表达式为：

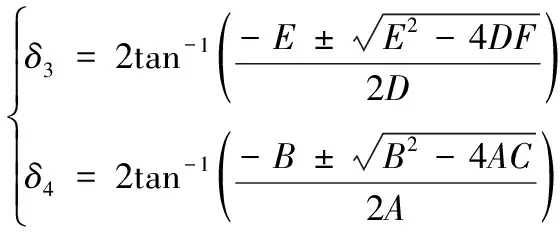
(4)

式中，A=cosδ2-L1-L2cosδ2+L3，B=E=-2sinδ2，C=L1- (L2+1)cosδ2+L3，D=cosδ2-L1+L4cosδ2+L5，F=L1+L5+ (L4-1)cosδ2。

M点横坐标和纵坐标在图1中的数学方程式分别为：

(5)

式中，(x0，y0)表示相对坐标系O1-X′Y′在绝对坐标系O-XY中的位置点，MX、MY分别表示四杆机构运动轨迹点在绝对坐标系中的横坐标和纵坐标，M1=d2cosδ2+pcosδ3-qsinδ3，M2=d2sinδ2+psinδ3-qcosδ3。

2 构造误差函数

2.1 几何参数设计变量

四杆机构几何参数尺寸变化时，其M点的运动轨迹也会随之发生改变。因此，优化参数变量选择d1、d2、d3、d4、p、q、x0、y0、δ1和δ2。由以上参数构成的设计变量为：

(6)

式中，δ2n表示主动连杆旋转角度δ2的n等份。

2.2 构造误差函数

(7)

主动连杆旋转角度的变化会导致四杆机构运动轨迹的变化，从而生成一系列运动轨迹点Mi，运动轨迹点Mi与δ2的关系式为：

(8)

因此，实际运动轨迹与理论运动轨迹所累积的误差函数为：

(9)

式中，N表示指定运动轨迹点的总数目。

四杆机构在实际应用中，通常将机架固定在某种机器中，其运动轨迹必然会受到额外条件的约束。通过约束条件构造出四杆机构运动轨迹最终误差函数，主动杆旋转过程，必须满足的约束条件如下：

(1)主动杆必须要能够作整周运动，由格拉晓夫准则[6]可知，四杆长度约束不等式如下所示：

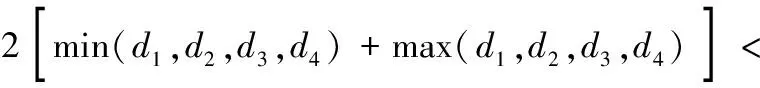
(10)

(2)必须按照从小到大或者从大到小顺序将主动连杆输入角度δ2i进行有序排列，取值范围[0,2π]。

(3)设计变量属于限定范围内，四杆尺寸为正值。

由理论与实际误差和额外约束条件误差两个部分最终构造出误差函数为：

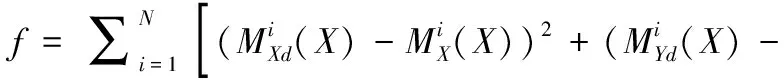
(11)

式中，h1(X)=0表示四杆机构主动连杆能够作整周运动，h1(X) =1表示四杆机构主动连杆不能作整周运动，h2(X)=0表示主动连杆输入角按照顺序排列，h2(X)=1表示主动连杆输入角不按照顺序排列，u1和u2表示约束因子。

3 混合粒子群算法

3.1 粒子群算法

粒子群算法是模拟动物群体觅食，通过迭代寻找最优解，从而构造出一种新的智能优化算法[7]。在粒子群算法求解过程中，根据群体极值G和个体极值Pi，粒子作出判断后，决定是否更新自身的速度和位置。粒子更新速度和位置方程式[7]为：

(12)

(13)

为了调节局部搜索能力和全局搜索能力二者的比例，惯性权重系数ω采取线性递减方程式[8]为：

(14)

式中，ω0表示初始权重，ω1表示最终权重，t表示当前迭代次数，T表示最大迭代次数。

3.2 混合粒子群算法

粒子群算法迭代次数越多，各个粒子相似度就会增大，容易产生局部最优解。因此，在粒子群算法的基础上增加遗传算法，把粒子个体和群体极值进行交叉和变异，从而搜索出全局最优值。具体操作步骤如下：

(15)

式中，r表示[0,1]区间内的随机数。

(2)变异。变异操作是为了保持种群的多样性，在个体中某点进行变异生成更优秀的个体，变异操作方程[10-11]为：

(16)

f(t)=1-r(1-t/T)a

(17)

式中，Amax，Amin分别表示个体的上界和下界，t表示当前进化代数，T表示最大进化代数，a表示可调参数。

4 误差仿真及分析

本文采用混合粒子群算法对四杆机构几何参数进行优化，初始条件设置如下：种群大小为100，迭代次数为300，惯性权重ω0=0.9、ω1=0.4，学习因子c1=c2=2，变异概率为0.6，交叉概率为0.01。采用混合粒子群算法优化后参数如图2、图3所示。

图2 连杆长度及坐标

图3 主动连杆旋转角度

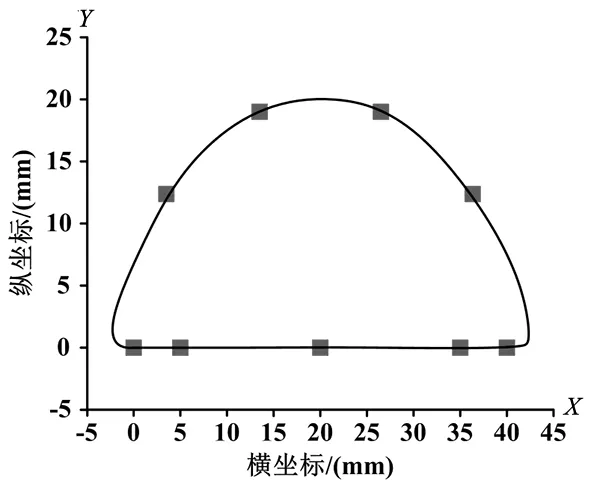
图4 目标点运动轨迹拟合曲线

M点实际运动轨迹误差采用Matlab软件进行仿真，横向误差优化前后仿真对比如图5所示，纵向误差优化前后仿真对比如图6所示。目标点运动轨迹横向和纵向误差优化前后数据对比如表1所示。

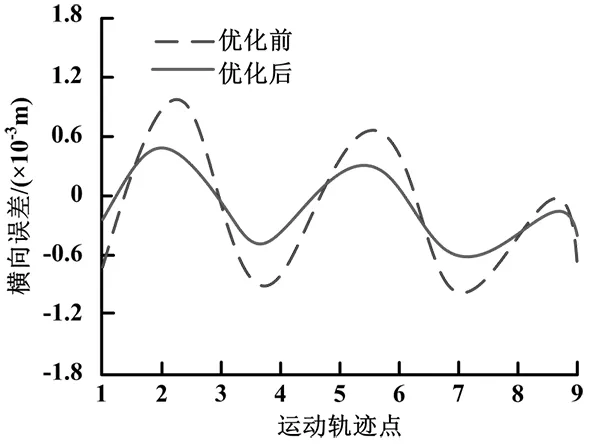
图5 横向误差优化前后仿真结果

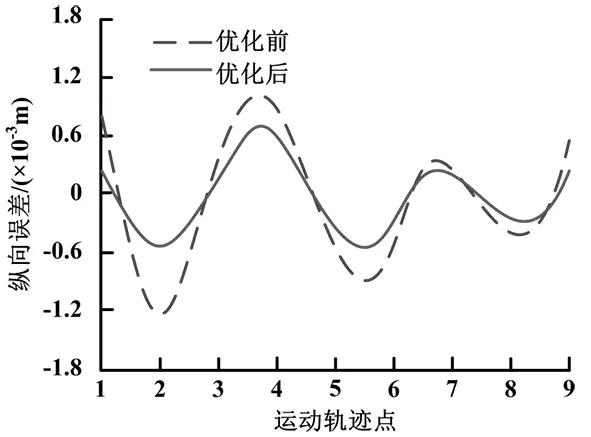
图6 纵向误差优化前后仿真结果

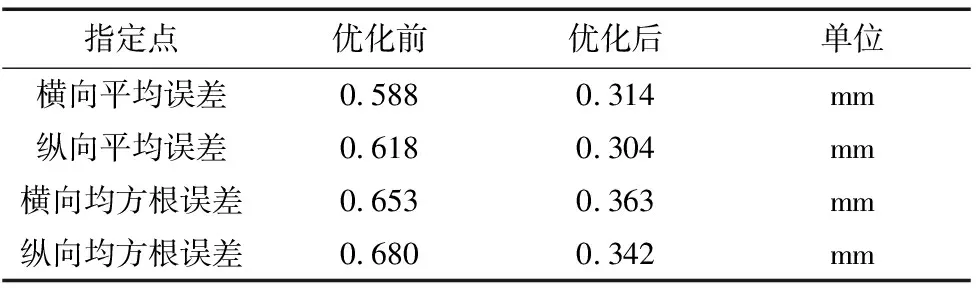
指定点优化前优化后单位横向平均误差0.5880.314mm纵向平均误差0.6180.304mm横向均方根误差0.6530.363mm纵向均方根误差0.6800.342mm

由图5、图6可知，横向和纵向优化后产生的误差峰值大幅度降低。由表1数据可知，横向和纵向平均误差在优化前分别为0.588mm和0.618mm，横向和纵向平均误差在优化后分别为0.314mm和0.304mm，横向和纵向平均误差优化后分别下降了46.6%和50.8%；横向和纵向均方根误差在优化前分别为0.653mm和0.680mm，横向和纵向均方根误差在优化后分别为0.363mm和0.342mm，横向和纵向均方根误差优化后分别降低了44.4%和49.7%。因此，四杆几何参数通过混合粒子群算法优化后，横向和纵向平均误差下降，误差波动程度也有所降低，四杆机构运动精度较高。

5 结束语

本文采用混合粒子群算法研究四杆机构实际运动轨迹的精度。在二维坐标系中建立了四杆机构示意图，采用矢量关系式推导运动轨迹坐标方程式。定义了四杆机构运动条件和设计参数变量，采用混合粒子群算法优化参数变量，将优化结果输入到Matlab软件中进行仿真验证。仿真数据表明，在相同条件下，优化后运动轨迹平均误差明显降低，误差波动幅度相对稳定，从而提高了四杆机构在实际应用中的运动精度，为多杆机构运动精度的研究提供了参考价值。