基于斜角切削理论铣削功率动态模型研究*

张学豪，赵 刚，王 强，阮 丹

(武汉科技大学 a.机械自动化学院；b.冶金装备及其控制教育部重点实验室；c.机械传动与制造工程湖北省重点实验室，武汉 430081)

0 引言

铣削功率动态预测模型是能耗评估不可忽略的重要环节，并且对于机床能耗评估具有重要意义[1-3]。目前铣削功率动态预测模型研究主要从两个方面着手：①单位体积切削能，②铣削力。文献[4]首先从单位体积切削能的角度很方便地求解出铣削功率，但是结果与实际情况差距很大,平均相对误差达到了16.06%，其次从铣削力入手建立的铣削功率模型精度明显得到了提高，平均相对误差减小到了3.7%。从铣削力入手研究动态铣削功率又可以细化为两类方法：①基于实际加工数据运用数学拟合方法建立材料去除功率动态模型，②基于材料去除机理的铣削功率模型。邵华等从铣削力的角度出发，以实际加工数据拟合铣削功率模型，建立了考虑铣削参数与刀具状态的铣削功率模型[5]。这种基于实际加工数据运用数学方法拟合得到的铣削功率经验模型精度很高，但是模型中的系数的确定是非常困难的，加工条件的多样性导致系数也是不一样[6]，并且模型适用范围很小，同时也体现不出铣削过程中的铣削机理[7]。

为了进一步克服上述困难,本文基于材料去除机理建立铣削功率模型。建立的铣削功率动态模型不仅考虑了铣削用量、刀具参数影响，同时也考虑了材料、摩擦和温度的重要影响。

1 铣削功率动态模型

1.1 铣削功率模型基础理论

由能量守恒定律可知,在铣削材料的过程中铣削功率由空载功率与材料去除功率组成：

P=Pmat-cut+Pemp

(1)

铣削功率P为铣削所需总功率，空载功率Pemp包括主轴旋转时消耗的功率、进给运动时消耗的功率、照明装置工作时消耗的功率和机床的基本模块工作时消耗的功率。空载功率Pemp与铣削功率P通过功率分析仪可直接测量得到，从而可以间接得到实际铣削材料过程中的材料去除功率Pmat-cut。

根据切削力计算铣削过程材料去除功率的表达式为：

P理论=Fτ·v+Fa·vz

(2)

式中，Fτ为切向铣削力，N；v为切向铣削速度，m/min；Fa为轴向铣削力，N；vz为轴向铣削速度，m/min。

切向铣削速度的表达式为：

(3)

式中，n为主轴转速，r/min；d为铣刀刀刃直径，mm。

轴向铣削速度的表达式为：

(4)

式中，β为螺旋角。

铣削功率动态模型是关于时间t的函数P=F(t)。每一时刻，通过沿轴向积分和对每个刀齿求和，得到作用于整个铣刀上切向、径向和轴向瞬时铣削力，然后将各方向上的铣削力与其对应的速度作乘积再求和，得到铣削功率动态模型。

1.2 斜角切削理论计算动态切削力

斜角切削理论的基本原理是首先将螺旋立铣刀复杂的铣削刃离散成无限小的斜角铣削刃单元，建立流动应力关于应力、应变率和温度的方程，其次运用数值方法计算出每个离散铣削刃的流动应力，代入流动应力值计算出每个离散铣削刃的切向、径向和轴向的微元铣削力，最后运用数值积分求和得到整体立铣刀各方向的瞬时铣削力,建立了实时反映铣削力的微分方程。

1.3 动态功率的数值仿真方法

动态理论铣削功率P理论表达式为：

(5)

动态理论铣削功率的MATLAB程序结构包含顺序结构和循环结构。循环结构最外层为角积分循环，中间层为刀齿积分循环，最内层为轴向积分循环。刀具以小的增量角旋转，沿铣削刃从底部到轴向铣削深度对各个微元铣削力求和，得到各方向的瞬时铣削力，最后得到动态理论铣削功率。

整体螺旋立铣刀的动态铣削功率数值仿真流程如图1所示。

图1 铣削功率仿真流程

2 斜角切削理论计算铣削力

2.1 圆柱螺旋立铣刀几何建模

圆柱螺旋立铣刀几何模型见图2。

图2 立铣刀几何模型

点P可以通过瞬时径向接触角Φjs确定：

(6)

其中，θ为铣刀旋转角；z为轴向深度；r为刀具半径；λs为刃倾角；N为刀齿数。

瞬时铣削厚度表达式为:

t=ftsinΦjsΓjs

(7)

其中，ft为每齿进给量；Γjs为啮合判别系数。

啮合判别系数表达式为:

(8)

2.2 流动应力计算

(9)

剪应变γ表达式为：

(10)

T关于Ze表达式为：

(11)

其中，T为绝对温度；ρ为材料密度；c为材料比热容；τ为剪应力。

流动应力表达式为：

(12)

2.3 铣削力建模

圆柱螺旋立铣刀各方向分力的表达式为：

(13)

在切向力和轴向力的基础上乘以各自对应的速度得到铣削功率如式(5)：

动态理论铣削功率P理论通过MATLAB程序得到。

接下来进行铣削实验验证，根据式(1)利用实验测量得到的实验数据计算出各时刻材料去除功率值与数值仿真得到的对应理论功率值，进行多点误差分析，判断模型的有效性。

3 实验验证

3.1 实验方案设计

铣削实验在FV-5224数控加工中心进行，主轴最高转速为4000r/min，进给速度范围为1～5000mm/min。

工件材料为45#钢，Johnson-Cook材料常数为：A=507MPa，B=320MPa，C=0.064，n=0.28，m=1.06；Tr=Tw=300K，Tm=1500K，ρ=7850kg/m3，c=500J/(kg·K)[9]，其他已知参数为：h=0.025mm，μ=0.85，f0=0.704，p=-0.248[10]。

刀具几何参数为：硬质合金立铣刀；铣刀刀刃直径20mm；螺旋角为30°，前角10°，后角15°；刀齿数3。

铣削方式为逆铣，无切削液。

铣削过程中用WT1800功率分析仪测量铣削功率，功率采集系统如图3所示。

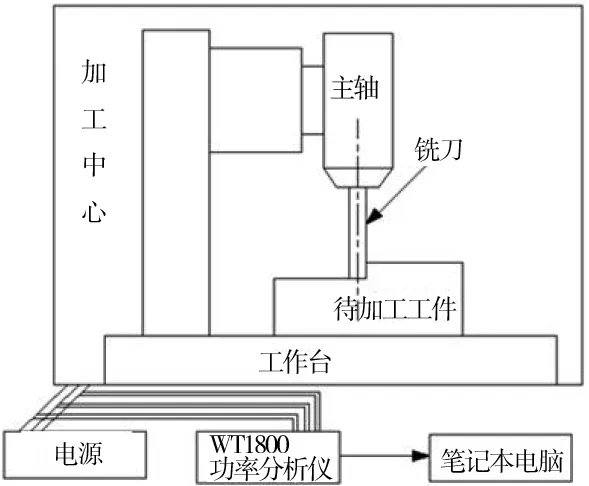
图3 功率采集系统

主轴转速、每齿进给量、铣削宽度和铣削深度为实验变量，如表1所示。

表1 铣削用量

每组实验分为3个工步，单个工步直线铣削120mm，铣削功率测试见图4，功率测量设备见图5。

图4 铣削功率测试

图5 功率测量设备

3.2 实验结果与讨论

由于第三组实验数据所得曲线特征较明显，以第三组实验第1次工步为例，对其实验曲线进行分析。铣削功率曲线如图6所示，材料去除部分(66s～137s)局部放大如图7所示。

图6 第3组实验第1次工步铣削功率曲线

将图7中各时刻测量得到的铣削功率减去机床的空载功率得到材料去除功率，然后与材料去除功率理论计算值进行对比分析，运用MATLAB软件得到理论与实测动态材料去除功率对比曲线，如图8所示。

图8 理论与实测动态材料去除功率曲线对比

从图8中可以看出，材料去除功率与理论铣削功率的变化趋势大致相同，但各个时刻对应的材料去除功率与理论铣削功率的差值不同，并且理论铣削功率数值小于材料去除功率的数值。

3.3 模型验证与计算误差

为了验证铣削功率动态模型的准确性，在铣削加工过程72s时间段内，随机选择第11s～25s,分别计算出每个时刻的材料去除功率，与其相应的材料去除功率理论计算值进行误差分析，判断铣削功率模型的准确性。

相对误差表达式为[11]：

其中，Ppred为理论铣削功率，W；Pmat-cut为材料去除功率，W。

11s～25s时间段，每个时刻材料去除功率与理论铣削功率的相对误差结果如表2所示。

表2 材料去除功率与理论铣削功率的相对误差

通过表2可以看出，最大相对误差为12.2%，最小相对误差为8.8%，误差分布在8.8%～12.2%区间，基本满足工程要求，验证了模型的可行性。铣削功率的理论预测值要小于实测值，主要由以下几个原因造成：①在铣削过程中，由于是干铣削，铣削过程中产生的高温会对刀具造成损伤，降低了刀具的铣削能力；②铣削过程中机床、刀具以及夹具都会产生较小幅度的振动，使铣削过程不稳定不利于铣削；③铣削功率模型没有考虑铣削刃与工件接触时产生的犁耕力作用。

4 结束语

本文建立了基于斜角切削理论的铣削功率动态模型。从铣削过程中材料的塑性变形和去除机理入手，分析了材料变形过程中应变、应变率和热软化效应对切削力变化的影响，结合铣削工艺参数如铣削用量、刀具角度等参数，建立实时反映切削力变化的微分方程，利用数值计算方法仿真斜角铣削过程的材料去除功率随时间的变化规律。并利用FV-5224数控加工中心干铣削45#钢进行的实验数据，在去除机床空载功率后与材料去除功率理论计算值进行多点比对，误差分布在8.8%～12.2%区间，基本满足工程要求。

铣削功率动态模型，不仅考虑到铣削用量、刀具参数影响，还考虑到材料、摩擦和温度的影响。未来要进一步做的工作是从振动的角度出发研究铣削功率动态预测模型。