北斗三频中长基线差分定位性能研究

于文浩,张云,韩彦岭,杨树瑚

(上海海洋大学 信息学院,上海 201306)

0 引 言

多频系统的发展和应用是各个卫星系统的研究热点,北斗卫星系统(BDS)能同时播发三个频点的信号,可以通过双频或三频信号的线性组合构成宽巷(WL)和超宽巷(EWL)组合,提高整周模糊度的解算性能,可在中长基线和长基线的差分定位解算中发挥优势。

三频模糊度固定算法简单并且可以避免复杂的搜索工作,被国内外学者广泛使用,并且对其做了大量研究工作。Teunissen等比较了不同的三频模糊度解算方法及其性能[1],包括利用宽巷组合逐步解算模糊度(TCAR)的方法[2-3],与TCAR类似的逐级整数解算(CIR)的方法[4],以及最小二乘模糊度解相关方法(LAMBDA)[5]。张云等针对不同长度基线评估了GPS三频模糊度解算性能[6]。冯延明提出了利用弱电离层组合虚拟观测量来评估GNSS三频模糊度解算性能并且使用该组合有效削弱了长基线电离层延迟误差[7]。李博峰等利用三频信号线性组合能组成超宽巷的优势,提出了一种长基线定位方法,深入分析了中长基线中的大气残余误差对定位精度的影响,还分析了三频电离层无关组合对模糊度解算的优势并提出一种窄巷模糊度解算方法并在后续的研究中将超宽巷直接应用到RTK定位解算中,而不进行窄巷模糊度的解算[8-10]。李金龙等将电离层无关组合应用到中长基线模糊度解算过程中[11]。唐卫明等提出针对三频最优组合方法,并通过不同长度基线评估三频模糊度解算性能[12]。黄令勇等利用北斗长基线三频数据,使用几何无关组合(GF)和电离层无关组合(IF)方法进行电离层延迟改正并评估模糊度解算性能[13]。赵齐乐等针对中长基线提出一种改进的三频模糊度解算方法[14]。张小红等使用北斗三频数据研究了LAMBDA算法、几何无关TCAR算法、几何相关TCAR算法以及无几何无电离层算法之间模糊度解算性能[15]。

上述研究主要运用了观测值线性组合并基于逐级解算思想进行模糊度求解,并且针对中长基线或者长基线主要分析电离层延迟误差对模糊度的影响,但是在中长基线的窄巷模糊度的研究中,将其构成卡尔曼滤波新息向量并且以此研究其对滤波性能影响的研究工作较少,本文将立足于此问题,并在上述逐级解算模糊度算法的基础上,使用相邻历元B3频段窄巷模糊度值构成卡尔曼滤波的新息向量,利用前一历元滤波值作为下一历元的预测值,通过整个滤波过程新息向量内积RMS值很容易分析出窄巷模糊度的误差对滤波性能的影响,并结合卡尔曼滤波的发散条件进行相关卫星历元筛选,最终可获得中长基线厘米级定位精度并有效缩短首次收敛时间,对北斗高精度差分定位有一定意义。

1 三频差分定位基本模型

本节简要描述三频观测值组合及模糊度解算,卡尔曼滤波新息矩阵分析等。

1.1 三频线性组合方程

Φr=ρ+cδT-rec-cδT-sat+δd-trop-δd-ion+

λBiNr+δΦ-hardware-delay+εΦr,

(1)

Pr=ρ+cδT-rec-cδT-sat+δd-trop+δd-ion+

δP-hardware-delay+εPr,

(2)

式中:Φr和Pr分别为北斗Bi(i=1,2,3)频点的载波相位和伪距的原始观测值(单位:m);ρ为卫星和接收机之间的几何距离;cδT-rec和cδT-sat分别为接收机和卫星钟差;δd-trop和δd-ion分别为对流层和电离层延迟误;λBi为北斗Bi频段的波长;δP-hardware-delay和δΦ-hardware-delay分别为伪距和载波相位的硬件延时;Nr为整周模糊度;εΦr和εPr分别为代观测误差量;xr,yr,zr为代接收机待求三维坐标;xs,ys及zs代表卫星位置。

考虑到中长基线大气误差的相关性减弱,容易受电离层,对流层影响,卫星i、j和移动站、基准站接收机r、b间的双差观测量为

(3)

(4)

使用北斗三频信号形成虚拟组合观测量,有助于整周模糊度的求解,基于原始观测方程,线性组合后的三频观测方程为[16]

P(l,m,n)=

(5)

Φ(i,j,k)=

(6)

式中:l,m,n及i,j,k分别为代伪距和相位的线性组合系数值；fB1,fB2及fB3分别为各个频点的频率；PBi和φBi分别为代双差观测值,线性组合后的虚拟频率值,波长及双差模糊度为

f(i,j,k)=i·fB1+j·fB2+k·fB3,

(7)

(8)

N(i,j,k)=i·NB1+j·NB2+k·NB3.

(9)

1.2 三频模糊度解算方法(TCAR)

三频模糊度解算方法(TCAR)是基于超宽巷和宽巷组合的一种逐级模糊度解算方法,本文采用两组超宽巷组合并结合电离层无关组合来解算窄巷模糊度。

本文选择几何无关电离层无关组合[P(0,1,1,φ(0,-1,1)]以及几何无关组合[P(1,1,0),φ(1,4,-5)]:

(10)

(11)

宽巷模糊度可以由两组超宽巷线性组合而成:

(12)

(13)

使用模糊度固定的超宽巷组合求解双差电离层残差值,因为线性组合形成比较大的组合观测噪声,通过多历元间平滑进行观测误差的削弱:

=K×[(ΔΦ(1,0,-1)+λ(1,0,-1)

λ(1,-1,0)ΔN(1,-1,0))],

(14)

基于伪距和相位的电离层无关组合解算模糊度:

(15)

最后通过上述宽巷模糊度NWL(1,0,-1),电离层无关模糊度值NIF以及窄巷波长λNL(1,0,1)计算B3相位观测值中的模糊度值:

(16)

1.3 卡尔曼滤波新息向量的构建

使用卡尔曼滤波算法,待求参数向量X如下:

(17)

(18)

式中: 将B3频段的窄巷模糊度之差作为卡尔曼滤波的新息向量；NNL为通过TCAR算法解算的B3频段的窄巷模糊度;Nestimated分为两种情况,对第一个历元进行解算时,Nestimated为通过最小二乘估计得到的B3频段模糊度初始值,后续的历元解算时,Nestimated为上一个历元的B3模糊度的滤波值,为了降低卡尔曼滤波对舍入误差的敏感性以及保证数值的稳定性,其待估参数的协方差矩阵Qt为下

(19)

本文中通过发散率以及新息矩阵的卡方均值来评估卡尔曼滤波的性能,发散率定义为发散历元数与总历元数的比例:

(20)

式中:Θ为卡尔曼滤波的发散率;Ndiverging为发散历元数;Nall为总历元数,判断卡尔曼滤波发散的标准如下:

(21)

式中:γ为发散系数(设γ≥1),如果上述判断不成立,表示滤波器的实际参数估值超过理论估值,滤波器发散,本文的研究中,设γ的值为1,并且假设噪声呈高斯分布,则当滤波模型构建适当的情况下,卡尔曼滤波的新息向量的二次型服从卡方分布,且卡方均值等于新息向量的维度,因此通过计算整个滤波过程的均值与其维度之比来判断卡尔曼滤波的精度,计算式为

(22)

2 实验设计

此次实验使用北斗三频实测数据进行中长基线RTK定位性能分析,移动站选择上海市张江高科技园区,基准站为上海海洋大学信息学院楼顶,基线45.5 km,使用两台北京和芯星通生产的UR370北斗三频接收机进行实地测量,采样频率为1 Hz.

图2示出了Google地图基线信息及移动站、基准站的相关配置,图3示出了移动站和基准站的天顶图信息,并且从图4中可以看到两站共同观测卫星数大部分为7颗卫星以上,可保证基本的定位性能,观测时间为UTC时间2017-04-24 03:00:01-09:30:00,卫星截止角设置为15°.

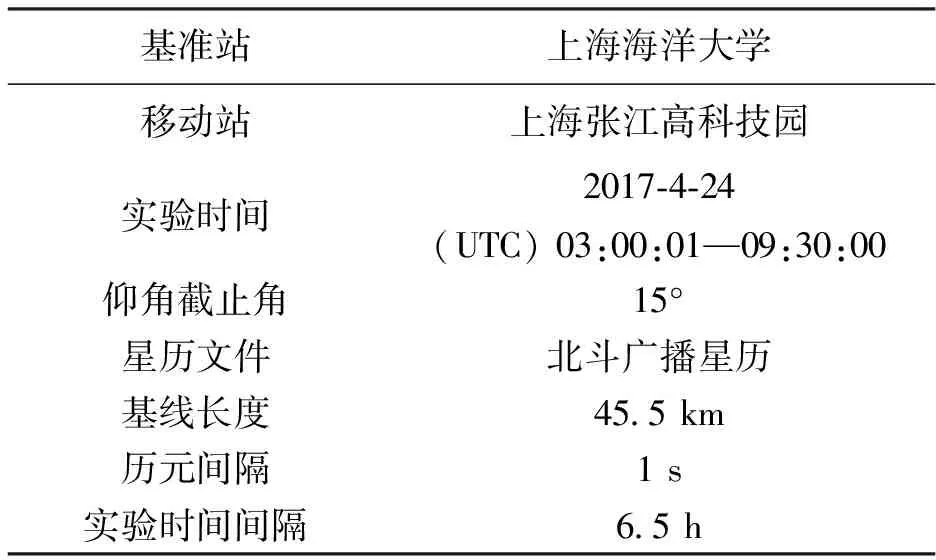
表1 实验基本信息

3 实验结果分析

3.1 双差电离层及对流层残余分析

双差大气残余误差是模糊度解算以及定位精度的制约条件,尤其是对于中长、长基线的差分定位中,因为其大气误差的相关性随着基线变长而减弱,采用Saastamoinen模型进行对流层误差改正并评估其双差残余量,通过图6可得其双差对流层残余量小于1.2 cm,因此本文忽略残余的双差对流层延迟及其对模糊度固定的影响,通过两组模糊度固定的超宽巷观测值组合(0,1,-1)和(1,4,-5)来求解双差电离层误差,通过图5(a)可得,因为组合观测带来的较大的观测噪声使得电离层误差被淹没在其中,对其使用多历元平滑方法,将电离层误差从混合的观测噪声中提取出来,可得其双差电离层误差集中分布在0.2 m,针对较大的双差电离层残余误差,使用电离层无关组合法并结合宽巷组合(1,0,-1)来解算B3频段原始双差模糊度。

3.2 卡尔曼滤波新息向量及定位结果分析

图7～9所示为每个卫星对(C01号卫星作为基准卫星)窄巷模糊度值所构成的卡尔曼滤波新息值,图7所示GEO卫星的新息值在一段时间内收敛,因此GEO卫星未作处理,图8(a)所示C06和C09号卫星的新息值逐渐发散可能会导致卡尔曼滤波发散,因此,将C06号卫星9550～10280号历元进行剔除,将C09号卫星11000～14621号历元进行剔除,C07,C08,C10号卫星不做处理,对MEO卫星使用相同的处理方法,图9(a)所示C12,C13号卫星的新息值跳变比较明显并且不易收敛,因此剔除C12号卫星3851～4129号历元,C13号卫星8524～8614号历元,C11和C14号卫星不做处理,图9(b)所示经过部分历元剔除后C12和C13号卫星新息值逐渐收敛。

为了评估卡尔曼滤波性能,分析了卡尔曼滤波新息向量内积RMS值,如图10(a)所示,很明显可以看出因为C06号卫星新息值的发散导致卡尔曼滤波发散,发散率为1.2%,因为C13号卫星新息值跳变比较明显,卡尔曼滤波新息内积出现相同的峰值,尚未发散,当进行部分IGSO和MEO卫星历元的剔除,如图10(b)滤波变得平稳且发散现象消失,另外模糊度固定成功的卫星对增加,如图11所示。

如图12所示,根据卡尔曼滤波新息值的异常变化将部分异常观测数据剔除后,窄巷模糊度浮点解和固定解之差主要集中在0.1周内,并且由表2可得大部分卫星的窄巷模糊度的固定率大于92%,然而C01-C03,C01-C14卫星对固定率较低，分别为64.81%和89.72%,由图13(a)可以看出卡尔曼滤波发散导致定位精度严重下降,其东向定位误差RMS值最大达到0.3 m,严重影响定位精度,当异常观测数据被剔除之后,其定位误差明显减小,如图13(b),但是因为C06号卫星的升降仍然呈现出定位结果跳变现象,表3所示为数据处理前后的定位精度相关指标,经过异常数据处理之后,东向定位误差RMS值由0.096 5 m降到0.058 4 m,北向定位误差RMS值由0.070 3 m降到0.046 9 m,天向定位误差RMS值由0.416 1 m降到0.324 3 m;固定率由95%提高到97.3%;卡尔曼滤波发散率由1.3%降到0.15%;定位首次收敛时间缩短近5 min;并且卡尔曼滤波的新息向量的卡方均值由0.768上升到0.992,更接近于1,使得滤波准确性得到保证。

表2 各个卫星对窄巷模糊度固定率

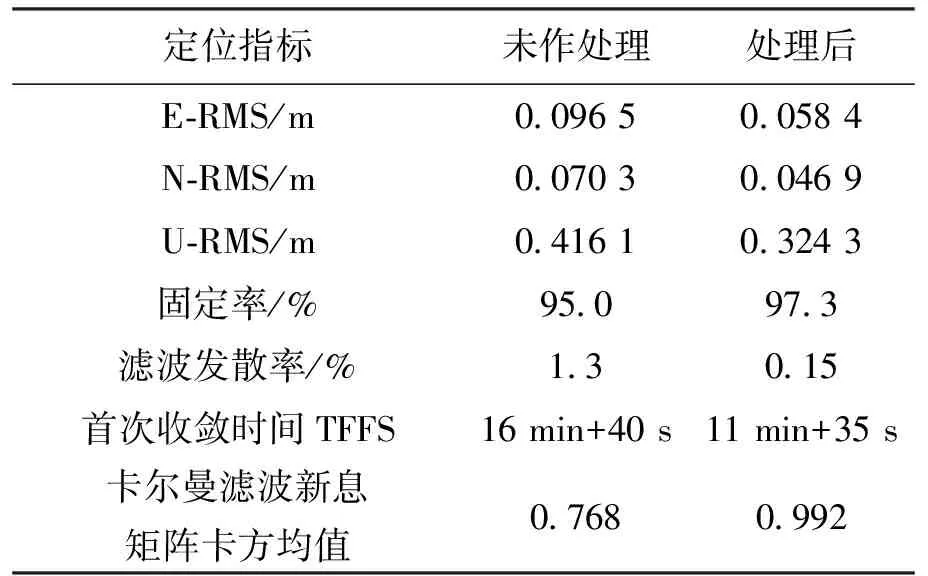
定位指标未作处理处理后 E-RMS/m0.096 50.058 4 N-RMS/m0.070 30.046 9 U-RMS/m0.416 10.324 3 固定率/%95.097.3 滤波发散率/%1.30.15 首次收敛时间TFFS16 min+40 s11 min+35 s 卡尔曼滤波新息矩阵卡方均值0.7680.992

4 结束语

本文主要分析了北斗卫星系统中长基线三频定位性能相关指标,包括使用两组超宽巷组合结合B3频段窄巷模糊度来评估双差电离层残差量;通过分析每个卫星对B3频段窄巷模糊度的新息向量来评估卡尔曼滤波的性能,并且通过滤波新息值内积均方根值容易判断窄巷模糊度的新息值是否逐渐发散从而可更方便地操作卡尔曼滤波过程,实验中检测到了部分IGSO和MEO卫星窄巷模糊度新息值的跳变现象，导致整个卡尔曼滤波发散以及定位精度的显著下降,通过剔除部分卫星观测历元解决了发散问题并且缩短首次收敛时间,提高了定位精度。