无人机软连接吊舱的伪卫星定位算法研究
荣凤娟,张清华,张杰,徐键卉
(陆军工程大学,江苏 南京 210007)
0 引 言
近年来,多旋翼无人机技术与装备发展迅猛,其灵活易操作特性使得许多科研项目选用它们作为载体[1-3],然而,某些科研仪器为了避免电磁干扰和物理震动,需与无人机机身保持距离,利用吊舱把科研仪器和无人机进行软连接是一种较好的选择[4-5]。通常情况下无人机自带有单频的卫星导航天线,但软连接情况,承载仪器的吊舱和无人机的相对关系受外界环境和风力影响,不能保持准确的相对位置关系,故需要对吊舱进行单独定位,以得到科研仪器的动态精确位置[6-7]。卫星定位为常见的实时高精度定位手段,但是在复杂环境下,如卫星可见性较差的,将无法定位,伪卫星是一种较好的可以灵活布设发射基站的定位设备,GPS作为常见定位手段,但在卫星可见性较差情况下无法定位,而伪卫星可以应对此类情况[8-9]。本文拟利用2.4 GHz无线测距装置作为伪卫星定位设备,在一定条件约束下对伪星的空间最优布设效果进行仔细深入的分析,并采用扩展卡尔曼滤波来应对伪卫星定位中的非线性问题,同时对定位结果与GPS进行了比较分析。
本论文的结构安排如下:第二章介绍了伪卫星定位设备的原理;第三章介绍了应用中伪卫星的定位算法,重点介绍了处理线性问题的扩展卡尔曼滤波算法,第四章为野外试验分析,包括现场的设置情况、空间星座分布的评估结果以及最重要的定位结果精度分析;第五章为总结和结论,从技术方法和工程试验效果等方面对本文的工作进行了评价,并分析了不足和下一步需要改进的技术方法。
1 伪卫星定位设备及定位原理
1.1 硬件组成
项目采用的是某公司提供的伪卫星系统,该系统的控制系统可以在一个标准笔记本电脑上流畅运行,它包含多个伪卫星发射装置(RN),并且具有测量距离的功能,同时还具有一个负责通信的终端(GW),测定两计算接收机(MN)的位置的距离,如图1所示。
在试验中采用了两种伪卫星发射终端,其中终端1既可以作为伪卫星发射基站,如图2(a)所示,又可以作为接收机使用,终端2只可以作为接收机使用,如图2(b)所示。
1.2 定位基本原理
与GPS定位的原理类似,该定位系统也是基于空间后方交会。伪卫星单点定位是以伪卫星发射基站和用户接收机天线之间的距离观测量为基础,并在已知精确伪卫星坐标的基础上来确定接收机天线所对应的观测点的坐标(x,y,z)。
则对于第i个伪卫星,它与接收机天线之间观测得到的距离量为
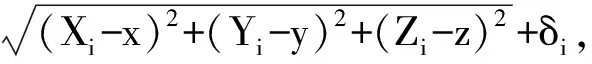
(1)
式中:Si为伪卫星和接收机之间的距离量,而第i个伪卫星的坐标(Xi,Yi,Zi)事先精确已知,则求解接收机坐标(x,y,z)至少需要三个以上的伪卫星。假设有三台以上的伪卫星同时对接收机观测(n≥3),则有以下线性化后的方程
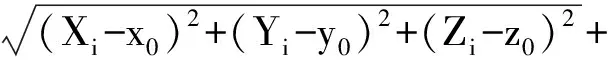
(2)

(3)
L=Hx+δ,
(4)
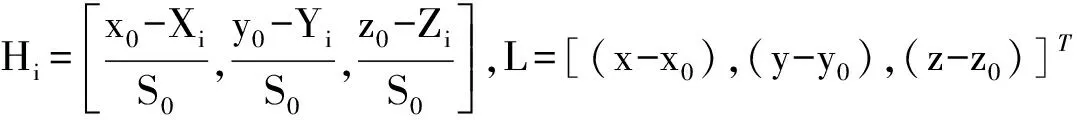
1.3 伪卫星空间分布评价(DOP)
DOP具有测量和代数的双重含义:在测量中代表GNSS卫星的几何结构所引起的伪距定位误差的比例,在代数中反映最小二乘平差权逆阵的迹特性。
在公式(4)中,设计矩阵为
(5)
式中:axi,ayi,azi(i=1,2,…,n)为接收机位置与伪卫星位置之间方向矢量的余弦,假设P为单位矩阵,则式(9)有如下形式
COV(x)=(HTH)-1σ2.
(6)
则PDOP、HDOP、VDOP可以由如下公式来表示
(7)
DOP值越小,则估计值x的协方差阵就越小,即具有更高的参数估计精度。
2 伪卫星动态定位的EKF算法
伪卫星定位系统与 GNSS 最大的不同点是伪卫星发射器一般距离用户接收机相对较近,这可能给定位过程带来一些有利的影响,例如不用考虑电离层对伪卫星观测量的影响,但是同时也会带来一些不利的影响,例如远近效应和线性化误差等。
在用滤波方法消除卫星定位数据中的随机误差时,可以使用最优估计的方法,将真实的状态(定位结果)从各种随机干扰中实时最优估计出来,但应用不同滤波器进行最优估计(滤波)时,需要建立较准确的系统模型和观测模型,而且要对各种随机误差进行准确地建模。目前国内外对将最优估计方法应用于滤波方面做了大量的研究,也取得了很多相应的成果。
通常最小二乘方法不考虑观测信号的统计特性,仅仅保证测量误差的方差最小。同时,最小二乘法的迭代仅仅考虑了当前的信号状况,没有涉及前面的信号状况。因此在伪卫星定位的过程中,对定位结果计算的稳定性估计不足。
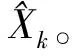
设动态系统的状态方程和测量方程分别为:
Xk=Φk,k-1Xk-1+Γk,k-1Wk-1,
(8)
Zk=HkXk+Vk.
(9)
为了减少线性化误差,学者们使用扩展卡尔曼滤波(EKF)。在考虑了泰勒展开的二阶项的条件下,二阶扩展卡尔曼滤波能使滤波性能得到改善。但是由于要同时计算雅克比矩阵和汉森矩阵,使得滤波计算量和不稳定性都大大增加。
EKF基于模型和观测模型统计信息,提供系统状态最小方差估计。状态方程和测量方程在其前一估计处进行线性化处理:
(10)
从而将非线性系统转换成线性离散系统形式,再利用线性卡尔曼滤波器进行估计。其算法具体实现如下[12]:
时间更新:
(11)
测量更新:
(12)
其中,Kk被称作卡尔曼滤波增益
(13)
虽然时间更新和测量更新中状态分别用非线性方程表示,但协方差阵使用线性化的方程进行传播。
3 野外试验分析
3.1 现场设置
为了对本试验中的六旋翼无人机软连接吊舱进行动态定位分析,本文的研究人员选取了位于南京汤山地区的一块平坦区域进行场地试验(如图3所示)。首先在场地的周围架设6个高度约15 m的铁塔,用于安装伪卫星基站的天线,而基站的初始位置由全站仪进行确定,其平面位置如图4所示,具体的基站坐标如表1所示。
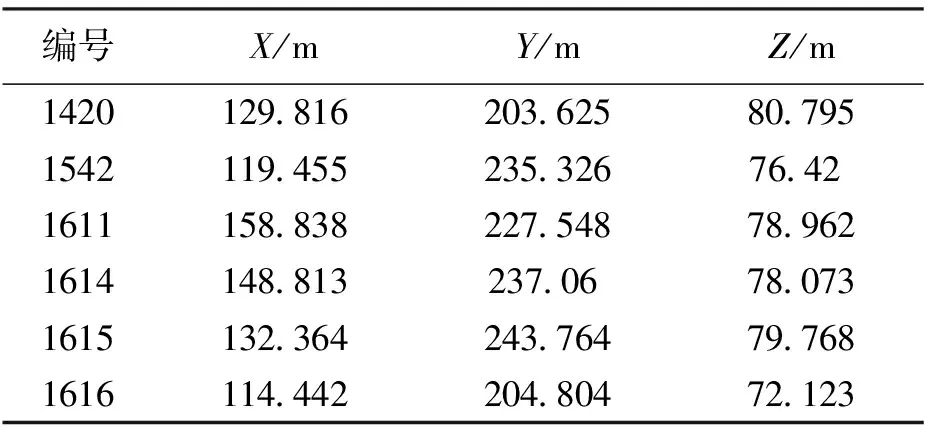
编号X/mY/mZ/m 1420129.816203.62580.795 1542119.455235.32676.42 1611158.838227.54878.962 1614148.813237.0678.073 1615132.364243.76479.768 1616114.442204.80472.123
为了对伪卫星定位的效果进行分析,试验采用GPS RTK 技术与伪卫星定位结果进行比对,以验证伪卫星定位的绝对精度。试验中将伪卫星观测站(OS)与GPS RTK天线采用捆绑的方式固定在一起,并利用软连接与无人机进行连接(如图5所示)。而图6为正在进行的动态定位试验,无人机飞行的范围在由铁塔围成的多边形区域内部。
3.2 空间星座构型
根据基站布设的位置,利用2.3节中的DOP值理论对试验场内的基站空间分布情况进行评价。其中图7(a)的浅色线条为无人机的飞行轨迹。图7(b)、7(c)和7(d)分别为PDOP、HDOP和VDOP的分布情况,可以发现,无人机的飞行区域基本位于DOP值较为理想的区域,非常有利于试验的开展。
3.3 定位结果分析
利用EKF算法对无人机软连接下的伪卫星观测站进行了动态定位,同时利用GPS RTK得到共位坐标。图8(a)~图8(d)分别表示了伪卫星和GPS定位三维和X、Y及Z方向的定位结果比较,通过比较可以发现,在绝大多数的时间内,二者定位的结果都比较吻合(如图8(a)所示),但在图8(b)的30~40 s的时间段内(灰色区域),伪卫星和GPSR TK的定位结果出现了较大的差异,此差异可能是由于无人机在X方向机动较快,而造成了伪卫星定位精度的降低。
为了进一步分析二者的差异,对伪卫星和GPS的定位结果进行差分比较,通过分析图9可以发现,伪卫星在X方向的定位结果比Y和Z方向略差,X方向是无人机行进过程的主要方向,相当于径向,其机动性最强。而且在X方向还存在数据跳变(Data jitter)的情况,这可能是伪卫星基站的不稳定造成的。对于误差分布,在X方向一定时间段内还存在着明显的误差漂移(Error drift),这可能是基站在X方向测距存在着累积误差。对于精度更好的Y和Z方向,其在无人机的起飞和降落阶段,同样存在着较大的误差(Larger errors),这可能是无人机初始运行的时候,机动性能较强且存在无固定规律的抖动造成的。
以GPS RTK测量结果为真值,对伪卫星定位误差绝对值的统计结果见表2.其中,X方向的最大误差为0.5 m左右,Y和Z方向的最大误差为0.2 m左右,三维方向的最大误差为0.5 m左右。三维平均误差优于0.2 m,标准差为0.15 m左右。伪卫星的定位精度基本可以满足未爆弹探测定位无人机对吊舱定位的需求。
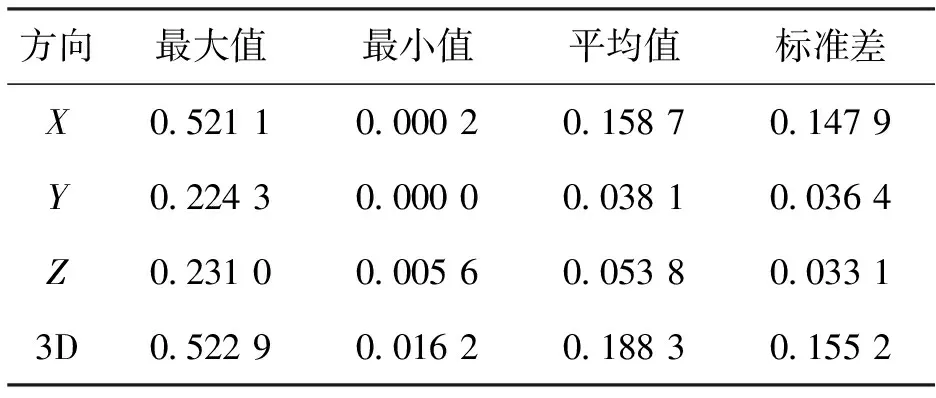
表2 定位误差绝对值统计
4 结束语
针对六旋翼无人机软连接吊舱的动态定位问题,论文在野外试验场地搭建了伪卫星定位系统,并利用EKF算法对吊舱的实时位置进行了估计。同时,试验中采用了GPS RTK定位的结果对伪卫星定位结果进行了评估,结果表明,采用此伪卫星系统及EKF算法可以在三维方向达到5 cm左右的精度,完全可以满足复杂条件下的无人机吊舱定位,可以很好地运用到实际工程中,为无人机定位提供了新的手段和方法,具有重要的意义。
但是,在无人机起降及机动性强的时间段,伪卫星的定位都存在较大偏差,需要在以后的研究中通过物理模型和数学加以改进。此外,伪卫星基站的持续稳定供电,也是下一步需要着重研究的工程化问题。

