制导火箭弹加速度信号处理及发射零时检测算法

袁毓雯，曹红松，程 炀

（1.中北大学机电工程学院，太原 030051；2.西北工业大学航天学院，西安 710072）

0 引言

制导火箭弹具有射程远、威力大以及精度高等优点，是对敌方进行火力打击的有效武器。制导火箭弹的发射零时作为靶场试验中的测量基准，对事后正确判定发射装置是否达到战术技术要求及弹丸飞行是否正常提供依据，为武器系统的后续改进和完善提供实际参考数据［1］。

用数值解法进行弹丸发射零时的检测是经典的作法，然而数值解法是建立在现有外弹道方程基础之上，发射零时判断精度过多依赖于弹载计算机的能力，且该方法数值计算量大、解算时间长和迭代过程中易产生大的累积误差［2］。近些年来，人们提出了5种发射零时检测方法：弹丸下方放置熔丝，起飞喷火时将熔丝熔断给出零时信号；导弹上方放置保险丝，起飞时撞断保险丝给出零时信号；导弹下方放置红外传感器，起飞喷火时红外传感器感应到温度的变化，温度上升到一定阈值给出零时信号；高速摄像机录像后，事后给出起飞的零时信号［3］；利用激光探测系统将经调制的激光照射在弹体上，一旦导弹起飞，离开发射座一定距离后，探测器探测不到（或探测到）反射光的这一时刻作为零时刻［4］。以上方法都或多或少地存在一些响应时间S级、误差大、实时性差、放置方式不够灵活等问题。本文针对此问题，给出数据信号处理的高可靠数学模型、求解算法及计算软件，利用施密特触发器原理的快速性等优点得到具有高精度的发射零时。

1 动态限幅法去除野值

火箭弹在实际飞行过程中，其加速度信息由弹载加速度计测量和保存。由于环境因素以及测量仪器的影响，导致收集到的加速度信号存在野值和噪声干扰。在进行后续的数据处理前，需要找到并修正野值点。

在火箭弹飞行过程中，弹载加速度计实时敏感和测量弹体运动的加速度，经过I/F变换电路实现将模拟信号数字化与弹载计算机相连［5］。本文通过数值模拟得到含有野值［6］和噪声的弹载加速度，如图1所示。

记采集到n个点的原始时间样本序列和加速度样本序列为ti0，ai0（i=1，2，…，n）；处理后的样本序列为ti1，ai1。通过采用动态限幅的算法查找并修正野值，递推公式如式（1）：

若动态限幅的阈值Δ取值过大，部分野值不能被有效地找到并修正，处理后仍存在；若Δ取值过小，会修改正常波动的数据。通过对原始样本数据分析可知，加速度在上升段最大变化值为194 m/s2。欲使原始数据不失真且能修正一定范围的野值，确定Δ=194 m/s2，处理结果如图2所示。

2 滑动窗口方式滤波

原始样本数据修正野值后，需要对新得到的样本数据进行滤波降噪处理。通过线性滑动窗口构造滤波器，可以很好地降低环境因素以及测量造成的随机波动对实测数据的影响［7-9］。记滑动窗口滤波处理后样本序列为ti2，ai2（i=1，2，…，n），滑动窗口滤波的模型如下：

式中，L为滑窗长度，Si为L个样本数据的和，averi为L个样本数据的算术均值。令L=2N+1，则滑窗长度的取值为奇数。在递推关系中，Si只需加上新的样本数据并去除x1i，即可得到Si+1，从而形成滑窗长度为L的环形缓冲队列。

2.1 均值处理

为了得到滑动窗口滤波处理后新的样本序列，有以下3种方案对averi的值进行处理。第1种为均值前置，将每次滑窗得到的averi赋给；第2种为均值后置，将averi赋给；第3种方法为均值中置，将每次滑窗得到的averi赋给。3种方案的处理结果（在加速度上升段）如图3所示。

显然，均值中值方案处理得到的结果和原始样本数据比较吻合。

2.2 滑窗长度L的确定

在选定方案3均值中置方案后，需要从滤波后样本数据的平滑度和灵敏度两方面分析滑窗长度L对数据处理结果的影响。分别取 L=3，5，7，9，11，13，15，分析滑窗长度L对滤波结果的影响。在水平段，经动态限幅修正野值后的样本幅值正常变化范围为0～170 m/s2。记滤波处理后水平段的样本幅值正常变化范围为δ，平滑度为S。处理后的结果见表1。

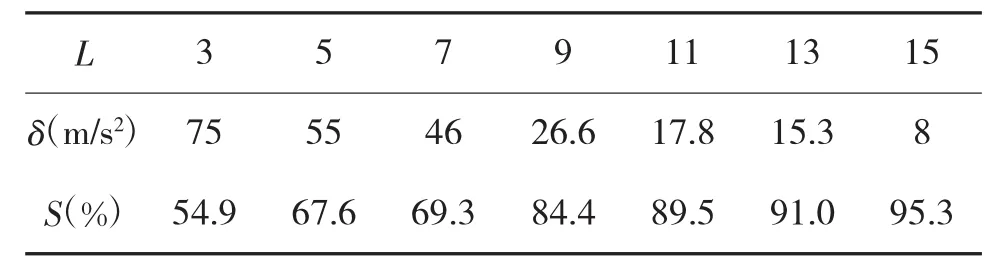
表1 滑窗长度L取值对平滑度S的影响

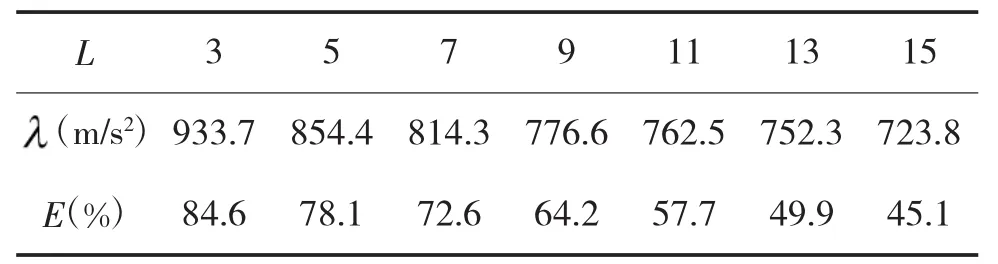
表2 滑窗长度L取值对灵敏度E的影响

由表1和表2知，L的取值与平滑度S正相关，与灵敏度E负相关，如图4所示。综合考虑，当L=7时，滤波的效果较好。因此，选择滑窗长度L=7。

原始采集的加速度样本序列经过动态限幅去除野值、滑窗滤波降噪处理后，结果如图5所示。

3 0状态线的确定

在发射前弹载加速度样本采集时，由于环境以及采集仪器等因素的影响，导致采集的样本值出现正常的波动。记发射前所在的状态为0状态，对处于0状态的序列做均值处理，随着序列长度M的增加，均值μ会趋于一个确定的值，即为0状态线。

4 发射零点判断

原始的加速度样本序列经过动态限幅去除野值、滑窗滤波降噪处理后，能准确地反映火箭弹加速度变化规律。在此基础上，运用施密特触发器原理进行发射零时判断。施密特触发器是特殊的门电路，具有两个阈值电压，分别称为正向阈值电压UT+和负向阈值电压UT-，两者的差值为回差电压。当输入电压从低电压上升到正阈值电压或从高电压下降到负阈值电压时，电路的高低电位状态将发生变化，如图6所示，uI增大时与正向阈值电压UT+比较，uI减小时与负向阈值电压UT+比较。

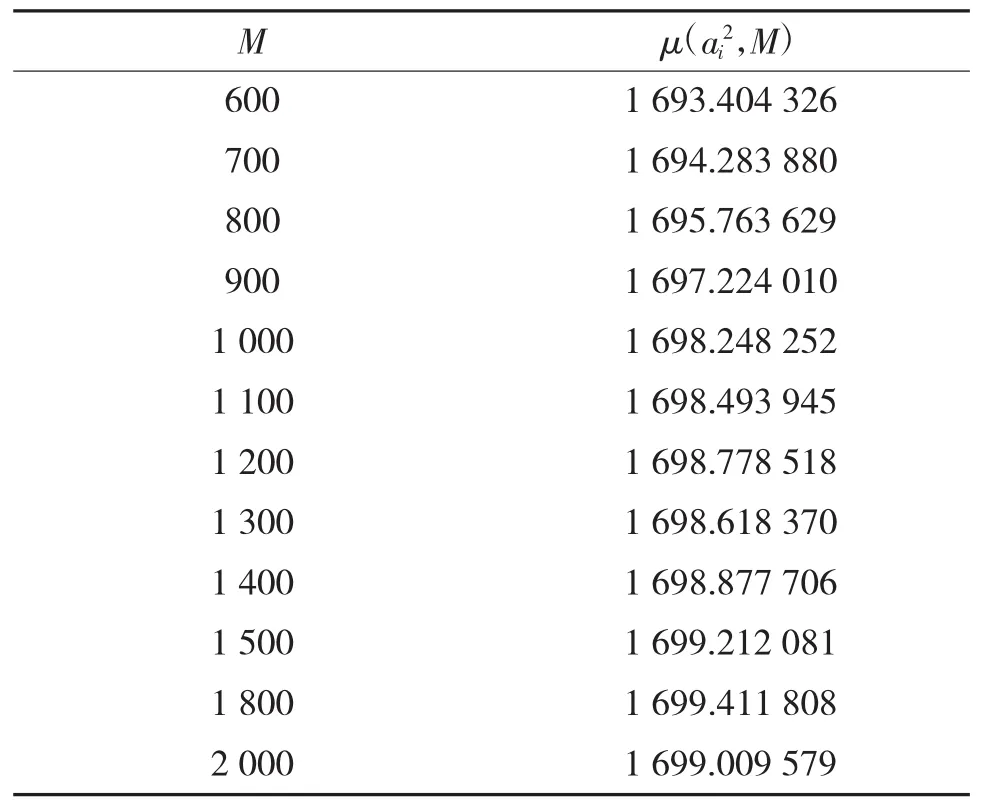
表3 不同M下的基线数值

利用该原理，若弹丸加速度由0状态线上升到正阈值加速度，且持续一段时间未下降，则可以确定制导火箭弹已经发射。记加速度样本采样时间为Δt，延迟判断的持续时间为T，触发时间为Ts，发射后第一次下降处最低点的加速度值为A*，正阈值加速度值为A+，则：

取延迟判断的持续时间为T=0.5 s，在T=3.006 s时触发，则真正的发射时间为3.006 s。结果如图7所示。

5 结论

为了快速高精度地判断弹丸发射零时，本文提出了基于施密特触发器原理的检测方法。以制导火箭弹为例，通过数值模拟得到含有野值和噪声的弹载加速度样本序列，经过动态限幅去除野值、滑窗滤波降噪和基线估计确定0状态后，能准确地反映制导火箭弹加速度变化规律。在运用施密特触发器原理进行发射零时检测时，对检测结果有影响的变量为限幅的阈值、滑窗长度、序列长度、判断延迟时间及正向阈值加速度值。采用控制变量的方法对以上变量进行分析，发现这些因素对发射点的判断没有较大的影响。因此，该程序算法能够有效地剔除测试过程中粗大噪声、过程干扰及环境噪声的影响，为武器检测系统快速提供高精度的发射零时，具有一定的通用性和稳定性。