基于截断奇异值低秩矩阵恢复的Canny边缘检测算法*

郭 伟，董宏亮，赵德冀

(辽宁工程技术大学软件学院，辽宁 葫芦岛 125105)

1 引言

边缘特征作为图像的底层特征，是图像分割、模式识别、计算机视觉等领域的研究基础，边缘检测结果的好坏直接影响着后续高层次的图像处理和分析。近年来，越来越多的新技术引入到了边缘检测算法中，如水平集[1]、距离图[2]、遗传算法、神经网络、Gabor滤波器[3]等。Canny是基于最小二乘法推导出来的多级边缘检测算子，因具有较好的信噪比和较高的检测精度而被广泛应用。由于经典的Canny边缘检测算法中使用的高斯滤波器是线性滤波器，在对图像进行平滑处理时，只考虑到像素间的空间距离关系，而没有考虑像素值之间的相似性，是从图像的整体结构来修改图像，使得图像变得模糊，边缘信息被平滑处理，因而定位精度和信噪比下降，在很大程度上影响了后续的工作。因此，许多研究者提出了改进型的边缘检测算法[4 - 14]，并取得了较为理想的效果。Canny算法虽然应用广泛，但也存在着不足，尺度较小的各向同性高斯核可以提取图像的细节变化，但对噪声非常敏感，而尺度较大的高斯核有较好的鲁棒性，但定位精度较低。由此，李德军等人[4]提出了基于双边滤波的图像边缘检测算法，不仅考虑了图像空间上的邻近关系，同时也考虑到了图像灰度上的相似性。此算法对于受低密度高斯噪声干扰的图像有很好的平滑效果，而对于受到椒盐噪声干扰的图像检测效果却不理想。考虑到脉冲信号对边缘检测的影响，戚晓伟等人[5]提出了改进的双边滤波算法，首先对图像进行中值滤波，在一定程度上减小了椒盐噪声的影响，由于中值滤波的效果受滤波窗口大小的影响，因此采用固定大小的滤波窗口很难达到理想效果。张洁等人[6]采用各向异性扩散方程来进行滤波操作，该算法虽然有效地去除了伪边缘，但对椒盐噪声的处理结果仍然不理想。马蒙蒙等人[7]采用空间尺度自适应的各向同性高斯滤波算法，自适应地获取空间尺度。凌凤彩等人[8]设计了新的梯度算子以及非极大值抑制的条件。李敏花等人[9]在Canny算法的基础上设计了自适应的高斯滤波器尺寸和滞后阈值，提高了边缘检测算法参数设定的灵活性，但该算法在含有脉冲信号噪声干扰的情况下仍存在着不足。而在实际生产应用中，由于传感器故障、光照等原因，会造成图像中出现噪声点或者离群点，这时传统边缘检测算法就显得无能为力。Thombare等人[10]结合分割所具有的广泛适用性和抵制噪声的优点，且基于块统计来计算阈值，提出了基于阈值分割的分布式Canny边缘检测算法。Canny算法敏感于噪声，在滤除噪声时容易失去弱边缘信息，且固定参数降低了算法适应性。针对这些问题，Rong等人[11]用重力场强度的概念代替图像梯度，并获得了引力场强度算子，提出一种改进的Canny算法。冯珂等人[12]首先利用非线性扩散滤波器有效去除噪声，保持图像的边缘信息；其次，在邻域梯度幅度的计算中考虑了像素对角线方向的梯度计算，进一步抑制了噪声的影响；最后，使用平均类间方差可以自适应地计算不同图像的双阈值。文献[13]对低秩矩阵恢复进行了理论分析，提出将矩阵分解为低秩矩阵和稀疏矩阵，由于其具有较强的鲁棒性，被广泛地应用于人工智能、图像处理、计算机视觉等领域。据此，牛发发等人[14]提出了基于鲁棒主成分分析法RPCA(Robust Principal Component Analysis method)的Canny边缘检测算法。将边缘检测算法作用于低秩矩阵上，从而实现对图像的边缘检测。RPCA应用于图像时，可以认为其将图像矩阵分解为无噪声图像矩阵和噪声图像矩阵之和，其中无噪声图像矩阵具有低秩性，噪声图像矩阵具有稀疏性。由于RPCA分解得到的主成分可以去除少量的椒盐噪声及离散噪声，所以在含有低密度椒盐噪声的情况下此算法得到了较好的检测效果。由于低秩矩阵数据具有较强的全局描述能力和抗干扰能力，能够更充分地利用相似块之间的非局部信息，更好地保护图像原有信息，因此，利用矩阵的低秩性可以较好地恢复出原数据矩阵，以达到较好的检测效果。

本文在研究了经典Canny算法以及低秩矩阵恢复相关知识的基础上，结合二者各自的优点，提出一种基于低秩矩阵恢复的Canny边缘检测算法，并提出一种新的凸优化模型及求解方法，将边缘检测算法直接作用于矩阵的低秩部分，既可以保留Canny边缘检测算法的优越性又能增强算法的抗噪抗干扰能力。

2 数学工具

本节简单地介绍一下本文与矩阵相关的基本概念。首先介绍一种非常重要的分解模式，即奇异值分解SVD(Singular Value Decomposition)。

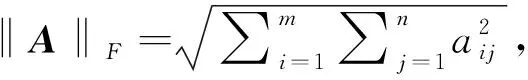
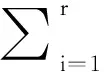
定义4[16,17]矩阵A∈Rm×n的奇异值分解为：A=USVT,S=diag({σi}1≤i≤min(m,n))，定义奇异值阈值算子：Θτ(A)=UΘτ(D)VT,Θτ(Σ)=diag(max{σi-τ,0})，其中σi是矩阵A中的第i个奇异值。

3 低秩矩阵恢复算法分析

低秩矩阵恢复又称鲁棒主成分分析或稀疏与低秩分解。从传统的主成分分析PCA(Principal Component Analysis)方法的角度来看待矩阵恢复问题，即传统的PCA方法是一种无监督的、使用SVD对复杂数据进行降维的方法，同时也可以认为其是一种去相关的方法，这种方法可以有效地找出数据中最“主要”的元素和结构，去除噪声及不相关部分，揭示隐藏在复杂数据背后的简单结构。PCA方法的本质是高维数据在其低维线性子空间上的投影，其目标就是使用另一组基去重新描述得到的目标空间，希望能尽量揭示原有的数据间的关系。可以表述成如下的数学模型：

min ‖S‖F,

s.t.rank(A)≤r,D=A+S

(1)

其中,D为输入的数据矩阵，S为误差项，‖S‖F表示矩阵的Frobenius范数，r为目标子空间的维数。通过上述的优化约束问题可以找到数据矩阵D在一个最近的r维的线性子空间上的投影，也就是说要估计这个低维子空间的数学模型就是要找到一个低秩矩阵A，使得其与观测矩阵D之间的差异最小化,称为损失最小化。当S服从Gaussian分布并且独立时，PCA方法可以通过一次SVD准确地找到最优逼近解A，此时PCA方法具有较好的表现。而当A受到稀疏噪声干扰时，PCA方法并不能很好地完成降维或者去相关操作，也就是说PCA方法对于离群点缺少鲁棒性，估计出的解往往不是最优解，并且PCA方法还需要预设目标子空间的维数r。于是Wright等人[18]提出了RPCA方法来解决矩阵中受到稀疏或者“污点”噪声干扰的情况。RPCA方法考虑的是这样一个问题：一般收集到的数据矩阵中包含结构信息的同时也包含噪声信息。那么，我们可以将这个矩阵分解为两个矩阵之和，一个是低秩的(由于内部有一定的结构信息，造成各行或列间是线性相关的)，另一个是稀疏的(存在的噪声是稀疏的)。与经典PCA问题一样，RPCA问题本质上也是寻找数据在低维空间上的最佳投影问题。对于低秩数据观测矩阵D，假如D受到随机(稀疏)噪声的影响，则D的低秩性就会破坏，使D变成满秩的。所以，就需要将D分解成包含其真实结构的低秩矩阵和稀疏噪声矩阵之和，以消除稀疏噪声的干扰。那么，RPCA可以描述成原始数据矩阵D由两个部分组成，即低秩矩阵A和稀疏矩阵S，原始数据矩阵可以表示为D=A+S。并且只要误差矩阵S是稀疏的，不论其大小，找到了低秩矩阵A，实际上就找到了数据的本质低维空间。那么,鲁棒主成分分析可以描述成如下的优化问题：

minrank(A)+λ‖S‖0,

s.t.D=A+S

(2)

其中,目标函数表示为矩阵A的秩函数及误差矩阵S的零范数，λ>0表示平衡因子，我们希望在合适的平衡因子λ的作用下能够精确地恢复出低秩矩阵A，然而，公式(2)的优化问题是一个NP-Hard非凸问题，在理论和实践过程中均只存在指数级复杂度的算法，并不能在多项式时间内直接求解。因此，需要寻找可以直接求解的优化问题来近似原问题。Candès等人[19]从理论上证明了L1范数最小化近似于L0范数最小化解，这样就可以将L0范数最小化问题松弛到L1范数最小化问题，而矩阵的rank()是非凸不连续函数，是奇异值的L0范数，而核范数是奇异值的L1范数，因此根据上述理论，可以采用凸松弛法，采用核范数来近似矩阵的rank()函数，L1范数近似L0范数。将式(2)转化为如下凸优化问题：

min‖A‖*+λ‖S‖1,

s.t.D=A+S

(3)

4 截断奇异值模型的提出

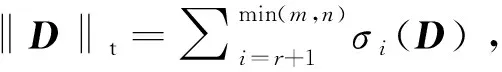
min ‖A‖t+λ‖S‖1,

s.t.D=A+S

(4)

然而，截断奇异值方法同样是非凸的，因此式(4)同样无法直接求解。根据矩阵相关知识，由定理1和引理1可以容易地推出如下结论：

(5)

因此根据式(5)，式(4)可以转化为求解如下优化问题：

s.t.D=Z+S

(6)

因此,本文根据截断奇异值模型提出基于截断奇异值的鲁棒主成分分析方法RPCA-TSV(Robust Principal Component Analysis method with Truncated Singular Value)。

5 新模型的提出及算法描述

根据文献[20]中相关介绍，用于求解鲁棒性主成分分析的方法是基于这样一个假设：原始数据矩阵由低秩矩阵部分和稀疏误差矩阵两部分组成。在现实中，图像在获取和传输的过程中往往会遭受到各种噪声的污染，尤其是高斯噪声，从而降低了图像的质量，给后续的图像处理带来诸多的不利影响。也就是说现实中的数据矩阵常常同时受到高斯噪声和稀疏噪声的干扰，使得算法受到噪声干扰而变得不准确。因此，本文提出一种新的凸优化模型，把原始数据分为低秩部分、稀疏噪声部分和高斯噪声三部分，并添加高斯正则化项，构造双噪声凸优化模型:

min ‖Z‖t+λ‖S‖1+β‖G‖F,

s.t.D=Z+S+G

(7)

其中,‖Z‖t表示截断奇异值，‖G‖F表示矩阵的Frobenius范数，作为高斯噪声的约束项，β为高斯噪声与低秩矩阵之间的权衡参数。

5.1 优化模型求解方法

求解凸优化模型的最优解是一个关键问题，实际上，各个模型均可以使用迭代阈值法[21]来求解，但其中存在着如何选取迭代步长和迭代次数的问题。针对迭代阈值法的缺陷，Lin等人[22]提出了加速近端梯度算法和对偶算法。加速近端梯度算法使用部分奇异值分解减轻了求解过程对奇异值分解的依赖，提高了求解鲁棒主成分分析问题时的收敛速度和精度，但是当奇异值个数小于某一阈值时，其收敛速度甚至比使用完整的奇异值分解还要缓慢。而对偶算法在求解的过程中只依赖于最大的奇异值相关主奇异空间，然而目前并不存在一个十分有效的方法来计算该主奇异空间。随后Lin等人[23]又提出了增广拉格朗日乘子法来求解优化问题，使得其迭代解能够收敛到该优化问题的精确解，并且耗时相对较少。

采用交替更新的方法，当更新矩阵Z时，固定矩阵S、Y和G，求解下面的优化模型：

(8)

其中,Θμ-1(D)为伸缩奇异值算子。当更新S时，固定其他三项Z、Y和G，求解下面的优化模型：

(9)

其中,δε(A)为伸缩绝对值算子。

当更新G时，固定其他三项Z、Y和S，求解下面的优化模型：

(10)

当更新Y时，固定Z、S和G，此时Y的更新公式为：

Yk+1=Yk+μk(D-Zk+1-Sk+1-Gk+1)

(11)

更新μ:

(12)

其中,ρ为大于1的常数，ε为大于0且比较小的正整数。文献[24]中给出ρ=1.5,ε=10-8。初始Lagrange惩罚因子μ=0.25/mean，其中mean是D中所有元素的平均值。

5.2 截断奇异值鲁棒主成分分析求解流程

交替迭代更新算法流程描述如下：

步骤1初始化数据矩阵以及迭代误差:

设定初始数据矩阵M=D，惩罚因子μ，迭代收敛误差eps=ε‖D‖F，终止误差ε。

步骤2计算中间变量Ak和Bk:

将初始化矩阵M进行奇异值分解即：[Uk,Σ,Vk]=svd(M)，其中Uk=(u1,u2,u3,…,um)∈Rm×n,Vk=(v1,v2,v3,…,vn)∈Rm×n，从而得到Ak=(u1,u2,u3,…,ur)T,Bk=(v1,v2,v3,…,vr)T。

步骤3使用交替更新方法求解式(7)的优化问题：

(1)用式(8)更新变量Z；

(2)用式(9)更新变量S；

(3)用式(10)更新变量G；

(4)用式(11)更新拉格朗日乘子Y；

(5)用式(12)更新惩罚因子μ。

直到内部算法收敛，即‖Zk+1-Zk‖F≤eps,‖Sk+1-Sk‖F≤eps,‖Gk+1-Gk‖F≤eps。

步骤4转到步骤2重复循环更新变量，直到外部算法收敛，即‖D-Z-S-G‖<ε‖D‖F。

5.3 本文边缘检测算法流程

本文算法首先求取输入图像的主成分部分，即低秩部分，然后将经典的Canny边缘检测算法作用于主成分上，最后输出边缘检测结果。算法流程如图1所示：

Figure 1 Algorithm flow chart图1 算法流程

6 实验结果与评价分析

6.1 算法评价指标

为了从客观的角度去评价一个算法的效果，本文采用以下评价标准。

6.1.1 峰值信噪比PSNR

采用峰值信噪比PSNR(Peak Signal to Noise Ratio)来评价图像的去噪效果，其定义如下[25]：

(13)

其中,L表示灰度等级的最大取值范围，本文中图像的灰度级为0～255;M，N分别表示图像的长度和宽度；i(x,y)表示原始图像;i′(x,y)表示去噪后的图像。PSNR越大表示去噪的效果越好。

Figure 2 Detection results of Lenna under salt noise of different densities 图2 Lenna图在不同密度椒盐噪声环境下的检测结果

6.1.2 品质因数FOM

品质因数FOM(Figure Of Merit)用于衡量边缘保存能力，其定义如下[26]：

(14)

其中,NID表示理想的边缘像素数目，NDE表示图像检测后的像素数目，di表示检测出的像素与离其最近的真实像素的距离，β是一个常量，一般取1/9。FOM是归一化的结果，其取值为0～1，与边缘的定位精度成正比，即FOM越大表示检测的边缘越准确。

6.1.3 边缘保持指数EPI

边缘保持指数EPI(Edge Preservation Index)用于评价边缘保持能力[27],其定义为:

(15)

其中,x表示无噪声原始图像，y表示去除噪声后的图像，Δ表示Laplacian算子。EPI的大小与边缘保持能力成正相关，其值越大表示边缘保持得越好。

6.2 实验结果分析

为验证本文算法的优越性，采用256×256像素的Lenna和Pepper标准图作为输入，由于各种算法在对无噪声图像进行检测时效果类似，而在处理含有椒盐噪声图像时，因较为敏感而没有很好的效果。因此，本文采用文献[5,14]以及本文算法对以下两种情况进行验证。

(1)仅受椒盐噪声干扰。

图2和图3分别显示了Lenna图和Pepper图在受不同密度(0.05和0.1)椒盐噪声干扰时各个方法的检测结果。图2中文献[5]的方法虽然可以很好地去除椒盐噪声的干扰，但是会丢失细节信息,其原因是文献[5]首先对图像采用固定大小窗口的中值滤波，然后再使用双边滤波进行处理，而造成了对图像的过度平滑，使得图像的检测效果下降。使用RPCA方法虽然可以得到较好的图像的边缘检测结果，同样也会把噪声当成边缘而进行误检，产生伪边缘。比如说图2中Lenna帽子上的伪边缘。而本文算法由于采用更加准确的表示方式来刻画模型中的秩函数而得到更加理想的边缘检测效果。表1显示了图2在不同密度椒盐噪声干扰情况下对应的评价标准结果，无论是在客观上还是在主观上，都可以看出本文算法的准确性较高、抗干扰能力较强。

(2)椒盐噪声和高斯噪声混合干扰。

为了验证本文算法的鲁棒性，针对椒盐噪声和高斯噪声混合噪声进行检测处理。图4和图5显示了受到椒盐噪声和高斯噪声混合噪声干扰时各个算法的边缘检测结果，检测图像中分别添加椒盐噪声(0.05)和高斯噪声(0.002)的混合噪声、椒盐噪声(0.1)和高斯噪声(0.002)的混合噪声。由于在鲁棒主成分分析过程中采用了更加精确的截断核范数形式来代替秩函数，因此本文算法的检测结果与RPCA方法相比更加准确；同时，本文方法增加了高斯噪声的约束项，使得在混合噪声干扰的情况下具有较好的检测效果。表2显示了图4所示的混合噪声情况下各算法对应的评价标准，从检测结果和评价标准可以看出，本文算法具有较好的检测结果，体现了本文算法的鲁棒性。

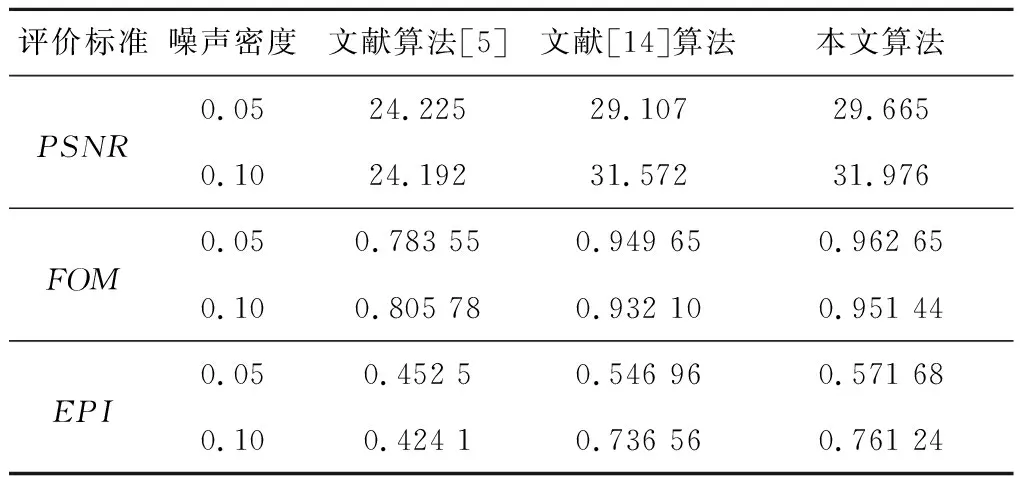
Table 1 PSNR,FOM,EPI of each algorithm under noise of different densities表1 不同密度噪声下各算法对应的PSNR，FOM，EPI

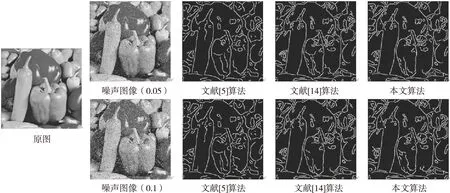
Figure 3 Detection results of Pepper under salt noise of different densities 图3 Pepper图在不同密度椒盐噪声环境下的检测结果

Figure 4 Detection results of Lenna in mixed noise environments with different densities图4 Lenna图在不同密度混合噪声环境下的检测结果

Figure 5 Detection results of Pepper in mixed noise environments with different densities图5 Pepper图在不同密度混合噪声环境下的检测结果

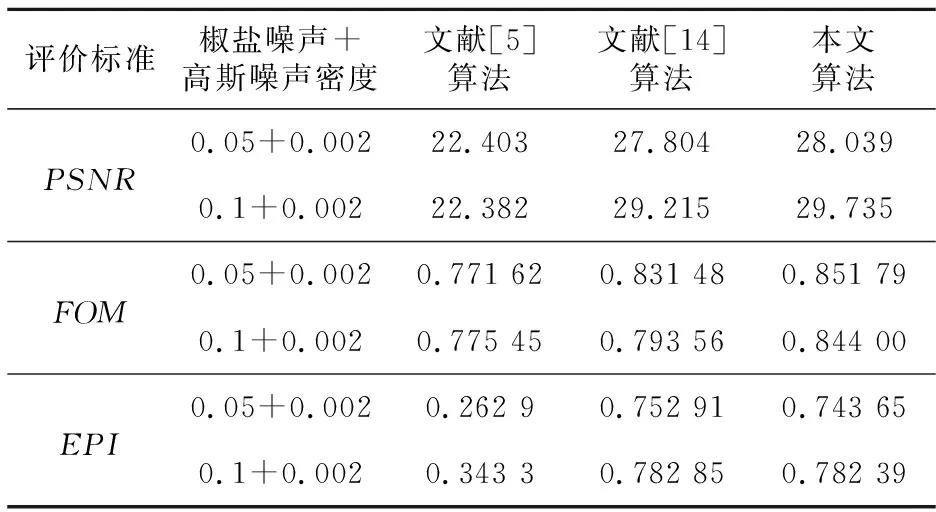
Table 2 PSNR,FOM,EPI of each algorithm under mixed noise environments with different densities表2 不同混合噪声密度下各算法对应的PSNR，FOM，EPI

7 结束语

针对图像边缘检测这一图像的底层特征提取问题，对于噪声图像，传统的边缘检测方法抗噪性能较差，往往不能很好地获取其边缘特征。本文通过改进的截断核范数鲁棒主成分分析方法将图像分解成低秩矩阵、稀疏误差矩阵和模拟的高斯噪声3个部分，去除原始数据矩阵中的稀疏噪声和冗余部分，起到增强原始数据矩阵的作用，有利于后续边缘信息的提取及图像处理工作。同时，结合经典Canny边缘检测算子的优点，将其作用于分解后的低秩主成分上。因此，本文算法可以很好地消除椒盐噪声以及混合噪声的影响，既能增加算法的鲁棒性，又能提高算法的去噪性能，提高边缘检测的准确性。