基于卷积神经网络的热轧带钢力学性能预报
胡石雄,李维刚,2,杨 威
(1. 武汉科技大学冶金自动化与检测技术教育部工程研究中心,湖北 武汉,430081; 2. 武汉科技大学高温材料与炉衬技术国家地方联合工程研究中心,湖北 武汉,430081)
当今钢铁市场竞争日益激烈,如何在不断改善钢铁产品组织性能的同时,缩短产品研发周期、降低生产成本,已成为钢铁企业亟需解决的问题。热轧带钢的力学性能预报是目前阶段钢铁冶金企业开发的重点技术之一,具有广阔的应用前景。现有的带钢力学性能预报模型的建模思路大致分为两种[1]:一种是机理建模,主要是基于实验室物理冶金学的实验结果,建立模型来预测产品的力学性能,如Irvine和Pickering提出了利用数学模型预测钢材组织演变及力学性能的方法;另一种是数据建模,根据实际生产数据,利用神经网络等智能算法来预测钢材的力学性能,如贾涛[2]、Bhattacharyya[3]等均建立了相应的性能预报模型。以上两种建模方法都取得了不错的成果,但也有不足之处:机理建模多以钢种为单位进行研究,局限性强;BP神经网络各层之间以全连接方式进行连接,不能很好地表达出影响因素之间复杂的交互作用关系。
卷积神经网络(Convolutional Neural Network,CNN)是近年来特别热门的深度神经网络模型。相比于传统神经网络,卷积神经网络采用的局部连接(Locally-connection)方式,有效减少了需要计算的参数个数。另外,权值共享方法可以使图像具有平移不变性,下采样操作可使图片具有一定的缩放不变性。目前,卷积神经网络结构已被广泛应用于自然语言分析、模式识别、图像处理等领域,但在工业生产领域内的研究应用尚不多见。
基于此,本文提出了一种将一维数值型数据转换成二维图像型数据的建模方法,并基于卷积神经网络结构LeNet-5和GoogLeNet,建立了热轧带钢力学性能预报模型,代入实际生产数据并通过对比实验对所建模型的有效性和准确性进行了验证。
1 相关工作
1.1 LeNet-5卷积网络结构
卷积神经网络LeNet-5[4]的基本结构如图1所示。由图1可知,该网络结构主要包括输入层、卷积层(Convolutional layer)、下采样层(Subsampling)、全连接层(Full connection)和输出层,其中卷积层和池化层(Pooling)交替出现,构成一个特殊的隐层。值得注意的是,输入图像需要经过大小归一化处理,每一个神经元的输入来自于前一层的一个局部邻域,并且被加上由一组权值决定的权重。提取到的这些特征在下一层相结合形成更高一级的特征,并且同一特征图的神经元共享相同的一组权值,次抽样层对上一层进行压缩,在减少数据处理量的同时保留了有用信息。

图1 LeNet-5卷积神经网络
1.2 GoogLeNet卷积网络结构
GoogLeNet[5]是2014年Christian Szegedy提出的一种全新的卷积神经网络结构,共有22个卷积层,相比于AlexNet[6]和VGG[7]等深度卷积神经网络结构,GoogLeNet在增加了网络深度和宽度的情况下,具有更少的参数和更小的计算量,其完整结构如图2所示。
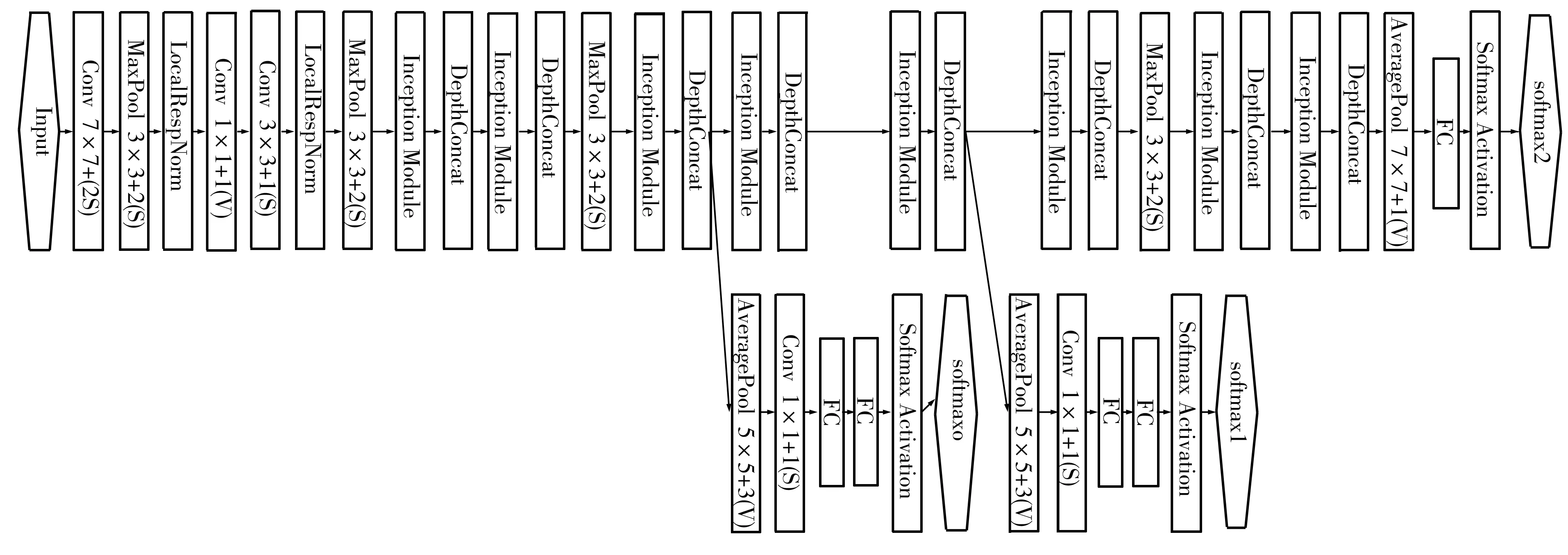
图2 GoogLeNet卷积神经网络
1.3 预测方法的融合
在LeNet-5和GoogLeNet网络结构基础上,本文提出了两点重要改进:一是将全连接甚至是一般的卷积均转化为稀疏连接[8],二是提出应用Inception结构于网络模型中,即在保证网络结构稀疏性的同时,又能利用密集矩阵的高计算性能。Inception结构模块如图3所示。在Inception结构中,笔者采用了不同大小的卷积核进行特征提取,最后将提取到的不同尺度特征进行堆叠(Concatenation)。相比于单一的卷积核,Inception结构具有更强的适应性。由于使用5×5的卷积核会带来巨大的计算量,故采用1×1的卷积核进行降维处理[8]。

图3 Inception模块结构示意图
2 带钢力学性能预报模型的设计
2.1 数据获取与预处理
获取某大型热连轧生产线的历史实际生产数据,基于随机森林算法和冶金机理筛选出重要影响因子,并剔除掉一些不可见干扰因素[9],最终得到44 760条带钢数据,每条数据中含20个影响因子和一个响应变量抗拉强度(Ts),所得实验数据集的具体组成如表1所示。
从表1中可以看出,具有不同特征维度的影响因子的表征含义、数量级及量纲单位不同,直接用于训练会影响模型精度,并且容易陷入局部最优解。因此,在开始训练前,需要对输入数据进行归一化处理,使各项数据指标之间具有可比性。原始数据经过标准化处理后,各指标处于同一数量级,模型收敛速度有所提升。
BP神经网络通常采用一维数值型数据进行建模,连接方式如图4(a)所示。由图4(a)可知,全连接层中每一个神经元均与输入数据中任一影响因子相连,无法表达出影响因素之间的局部交互作用关系,且需要计算的参数较多,故卷积神经网络采用如图4(b)所示的局部相连方式。
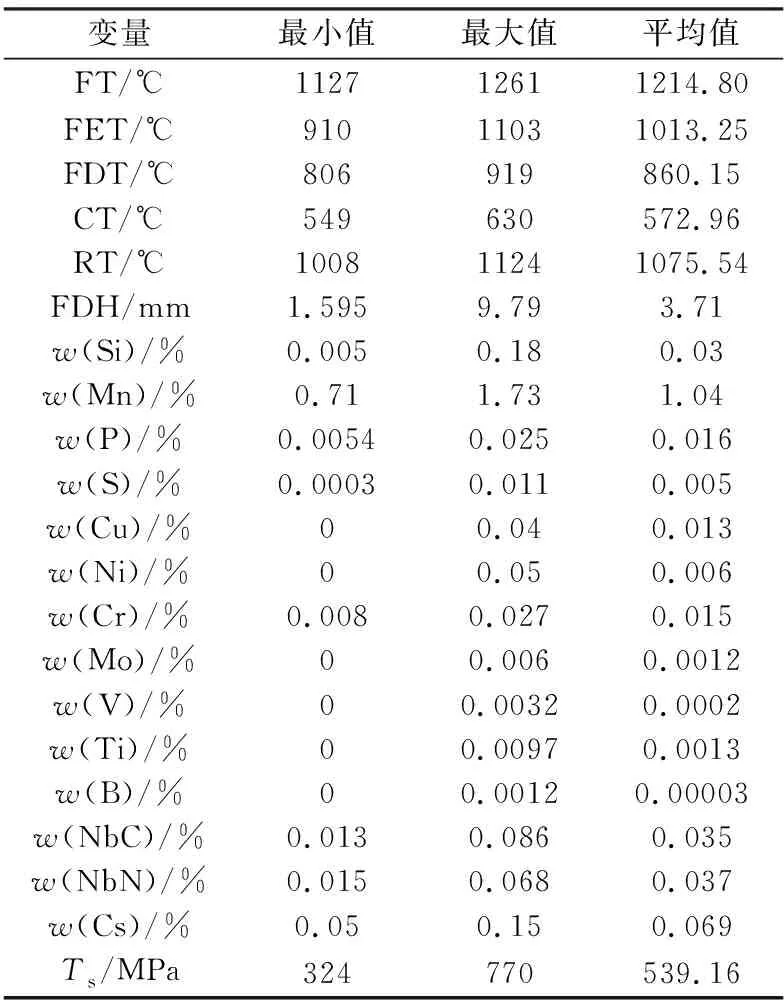
表1 实验数据集的组成
注:FT为出炉温度;FET为精轧入口温度;FDT为终轧温度;CT为卷取温度;RT为粗轧出口温度;FDH为终轧厚度。
在对图片进行卷积处理的过程中,影响因子通过不同大小的卷积核与周围其它影响因子局部相连,从而得到影响因子之间的局部交互作用关系。由于卷积核具有权值共享特性,故相比于BP神经网络,卷积神经网络具有更少的参数和更小的计算量。数字图像本质是一个多维矩阵,而传统的一维数值型数据表示的是一个一维矩阵,将一维数值型数据转为二维图像型数据实际是将多个一维矩阵进行拼接的过程。相比于一维数值型数据,二维图像型数据信息结构更为丰富,进行特征提取时能获取的有效信息更多。
在进行数据转换之前,首先需要确定图像的尺寸,即图像的高和宽。由于图像高和宽的乘积需要远远大于影响因子个数,故决定将一维数值型数据转换成大小为32×32的二维图像型数据,

(a)BP神经网络 (b)卷积神经网络
图4不同神经网络的连接方式
Fig.4Connectionmethodofdifferentneuralnetworks
其中共包含1024个像素点。依次将与带钢力学性能相关的20个影响因子填入1024个像素点中,每个像素点值的大小代表图片中该点位置颜色的深浅,每个影响因子被填入51次左右。该步骤主要是利用Python编程完成的,大致转换过程如图5所示。

图5 数值型数据转换成图像数据过程示意图
2.2 模型结构确定
由于本文所建立的热轧带钢力学性能预报模型的影响因子较少,直接使用较深的卷积神经网络结构难以取得好的效果,而使用太浅的模型结构精确度往往不高,故需要进行对比实验来确定模型中卷积层的层数。本研究利用Inception结构替代LeNet-5结构中的卷积层,选取均方根误差(RMSE)和平均绝对百分误差(MAPE)作为模型准确性的评价指标,即:
(1)

(2)

其余参数相同时,不同Inception结构数量下模型的计算偏差如表2所示,可以看出,当Inception结构个数选取为3时,模型具有较高的预报精度。
表2不同Inception结构个数的实验结果
Table2ExperimentalresultswithdifferentInceptionnumbers

编号Inception结构数量/个RMSE/MPaMAPE/%1131.463.492321.072.673524.482.794727.322.745929.103.12
图6即为本研究采用的卷积神经网络模型结构。考虑到输入图像尺寸(32×32)较小,故不适合使用太大的卷积核和步长,本文所用卷积核最大为5×5,步长均为1。输入图像经过Inception1进行特征提取之后,接一个最大池化层(Max pooling),卷积核大小为3×3,步长为2。该模型中的池化层均采用最大池化,这是因为相比于平均池化(Average pooling),最大池化能更有效地减少卷积层参数误差所造成的估计均值偏移,其原理如图7所示。
从图6中可以看出,模型经过Inception3之后接一个全连接层FC1,模型中最下方的FC2与输入图像直接相连,采用的是全连接方式,其能在一定程度上对卷积神经网络提取特征起到补充作用。最后将FC1和FC2提取到的特征进行融合,经过全连接层FC3后得到输出结果。

图6 本研究采用的卷积神经网络模型结构

(a)最大池化 (b)平均池化
图7最大池化和平均池化的原理示意图
Fig.7Schematicdiagramofmaxpoolingandaveragepooling
模型中采用的的激活函数均为ReLU函数,可表示为:

(3)
LeNet-5模型中,激活函数为Sigmoid函数,表示为:
(4)
相比于Sigmoid函数,ReLU函数有以下优点:①选取Sigmoid函数为激活函数,当Ni=f(Wi⊗Ni-1+bi)过大时,函数导数趋于0,这会造成信息丢失,降低模型的准确性。②当Ni=f(Wi⊗Ni-1+bi)<0时,ReLU激活函数的输出为0,在一定程度上造成了网络的稀疏性,这不仅减少了参数之间的相互依存关系,还缓解了过拟合问题;③ReLU函数的求导计算相对简单。
2.3 卷积神经网络模型训练
卷积神经网络模型不断通过训练样本进行学习,在信息的前向传播中求出预测值,并与实际值比较得到误差。若误差超过设定阈值,则进入误差反向传播阶段,在此阶段不断更新权重和偏置,直到预测值与实际值的误差低于阈值且误差不再下降时停止训练,得到最终需要的热轧带钢力学性能预报模型。
3 实验与结果分析
3.1 实验环境
本实验在Windows10 64bit 操作系统下进行,CPU为Intel(R) Core(TM) i7-6700,内存为16GBDDR4,GPU为NVIDIAGeForceGTX745(4 GB显存),显卡驱动为CUDA8.0+CUDNN5.1,编译环境为TensorFlow+Python3.5.2。采用开源深度学习工具TensorFlow作为卷积神经网络框架,并利用GPU加速整个训练过程。
3.2 参数选取
实验开始之前,需要配制卷积神经模型的相关参数,具体数值如表3所示。表3 中,Learning_rate表示学习率;Iteration_nums表示模型训练次数,如果模型的代价函数低于设定阈值且基本不再变化时,也可主动终止训练;Batch_size表示每次读入图片的批量,该值的选取需要根据实际输入图片的大小以及计算机内存和显存的大小关系来确定,本研究使用GPU加速训练,故需要保证每次读入批量图片小于显存大小;Dropout表示以一定概率舍弃神经元,其能有效防止过拟合的发生。

表3 模型参数
选取44 760条数据中的后4760条数据作为测试集,剩下的40 000条数据作为训练集。关于卷积核数目与神经元数目的选取,本文采用如表4所示的Inception模块参数以确定最优解。表4中Inception1、Inception2和Inception3的6个参数分别代表Inception结构中从上往下卷积核Conv1×1+1(S)、Conv3×3+1(S)、Conv1×1+1(S)、Conv5×5+1(S)、Conv1×1+1(S)和Conv1×1+1(S)的个数,FC1和FC2表示全连接层FC1和FC2的神经元个数,FC3中神经元个数为FC1和FC2中神经元数目之和。每次实验训练到代价函数趋于稳定才终止。从表4可以看出,采用第6组Inception参数的模型预测精度最高,模型MAPE值为2.49%,RMSE值为19.15 MPa。

表4 不同Inception参数下的测试结果
3.3 结果分析
选取第6组Incepion模块参数作为本文模型采用的参数,得到模型中损失函数值(Loss)与训练次数的关系如图8所示。从图8中可以看出,模型训练12 000次左右时已趋于稳定,在不增加数据量的情况下,模型的Loss值基本保持不变。故从测试集中取100条数据的预测值与实际值进行对比,结果见图9。由图9可知,基于本文所建模型的带钢抗拉强度预测值与实际值拟合情况较好,模型的适用性得到了验证。
为进一步验证所建模型的有效性,利用BP神经网络、LeNet-5和GoogLeNet三种模型分别对测试样本进行带钢力学性能预测,并选用均方根误差和平均绝对百分误差作为模型精度的衡量指标,结果如表5所示。由表5可见,本文所建模型的误差指标均低于其他模型的预测值,而直接利用卷积神经网络GoogLeNet模型的预测精度低于其他方法,尽管其深度优于LeNet-5和本文所建模型,表明在热轧带钢力学性能预报问题上模型的预测精度并不完全取决于模型深度。另一方面,LeNet-5模型中,卷积层数目较少且卷积核过于单一,模型的提取特征能力不够,适应性不强,导致其预测效果不佳。

图8 损失函数值随训练次数的变化
Fig.8VariationofLossfuctionvaluewiththeiterationtime

图9 带钢抗拉强度的预测值与实际值对比
Fig.9Comparisonbetweenpredictedandactualvaluesofstriptensilestrength

表5 不同预测方法的评价指标
4 结语
针对热轧带钢的力学性能预测问题,本文提出一种将一维数值型数据转换成二维图像数据用来建模的方法,相比于传统的一维数值型数据,二维图像型数据中结构信息更丰富,能提取到的有效信息更多。文中引入卷积神经网络来构建影响因子之间的局部相互作用关系模型,基于GoogLeNet和LeNet-5卷积神经网络结构的优点搭建带钢力学性能预报模型,并通过一个全连接层与输入层直接相连,将提取到的特征与卷积神经网络提取到的特征相融合。为验证该方法的有效性,文中代入某大型热连轧生产线的44760条历史实际生产数据进行测试,结果表明,与BP神经网络及单独的GoogLeNet和LeNet-5卷积神经网络结构相比较,本文所提方法的预测精度更高,本研究为热轧带钢力学性能预报建模提供了新的思路。

