基于MOEA和SE-DEA的四站器材应急供应策略研究

孟曦曦， 黄之杰

(空军勤务学院 a.航材四站系，b.基础部，江苏 徐州 221000)

0 引 言

航空四站保障主要为战机的地检与启动任务提供气、电产品和服务，是空军战斗力的重要组成部分。特殊任务下，在多机种保障机制、高强度保障任务以及复杂战场环境下，四站装备抢修器材的消耗量大幅上升，且要求的装备故障停机时间大幅缩短。因此，为四站抢修器材的应急供应提出了严格的要求。

针对该问题，①军内学者展开了相应的研究。陈卫华等[1]主要针对提升四站装备修理厂的应急保障和供应能力提出了相应建议；闫新丽等[2]对建立战时四站器材供应网络制定了详细的预案；许新明等[3]主要考虑了多机种保障时的战时四站抢修器材供应策略。②国内外有许多针对器材供应链的相关研究，Javid等[4]提出了一种随机供应链供应决策优化的模型。并将问题转化为一个混合整数凸程序，建立了一种基于禁忌搜索和模拟退火混合的启发式求解方法；Sepideh等[5]研究了在3级供应链中考虑选址和分配决策的供应模型，提出了一种有效的帝国主义竞争算法和一种禁忌搜索算法进行求解；Wilhelm[6]考虑了供应节点间存在横向供应的备件供应策略。

目前的研究仍存在几点问题，①军内研究以预案为主，缺少技术性研究。②地方研究与四站专业结合不紧密，未能满足紧急任务时特殊情况下的要求。在模型和算法上，①多以单目标优化模型为主，②多目标优化中产生的帕累托解集规模较大，不利于决策者的进一步决策。本文正是针对以上问题进行了相关研究。

1 四站抢修器材应急供应模型

1.1 问题描述

紧急任务环境下为保障多机种协同作战，四站保障涉及专业多，器材品种、型号多，电、气等需求量大，任务量大、出动频繁；同时，面临恶劣的战场环境，损伤大、故障多。为在最短时间内恢复四站保障分队战斗力，应建立3级供应网络，由战区四站厂和航材库联合作为后方仓库，根据仓储情况，向下一级仓库进行供应。同时成立中间支援点接收上级供应的器材，并组织运力将器材供应到各个需求点。各个作战单元作为需求点根据装备故障和损失情况，向基地级仓库提出需求。最终构成多资源点，多种器材的供应网络，如图1所示。

图1 四站抢修器材应急供应网络

1.2 建立模型

根据问题描述建立相应的供应模型。该模型须满足以下假设条件：

(1) 每个需求点器材需求量均可获得；

(2) 备件由后方仓库向中间支援点进行供应补充，再由中间支援点向装备使用分队进行供应；

(3) 各节点之间的路径信息已知；

(4) 各装备使用分队对器材的最低满足率给定。

在器材应急供应中，由于优先考虑的是在最短时间内最大限度满足作战的需要，而成本问题不作为必须的约束条件。因此，模型选用供应所需时间最短和需求点器材的满足度最大为两个目标函数，以时间和各个中间支援点的运力为约束构建如下模型。

(1)

(2)

式(1)表示供应时间应当最小，当两个节点之间没有供应关系时，决策变量的值为零，所用时间也为零。通过符号函数实现该功能。式(2)表示需求点的总器材满足率应当最大，即最大限度的满足作战单元的四站抢修器材。式(3)表示供应量约束，即对于每个中间支援点的供出量应当不大于供入量。式(4)表示每个中间支援点的供应量应当不超过其最大运力，最大运力通过器材的质量进行衡量。式(5)表示需求点四站器材供应满足率应当大于1而小于最大满足率。式(6)表示每个需求点的供应量应不小于其需求量。约束(7)指调度过程中的器材数量均为正整数。

2 多目标优化决策方法

2.1 多目标进化算法

进化算法被广泛用于解决多目标优化问题(multi objective problem, MOP)，被称为多目标进化算法(multi objective evolutionary algorithm，MOEA)。由于在多目标工程问题中，各个目标函数通常是相互冲突的，而不可能找到一个解，使得所有目标均达到最优。为解决这个问题，最常用的方式是求得帕累托非支配解集[7]。多目标优化问题中经典的进化算法包括SPEA2[8](Strength Pareto evolutionary algorithm 2)、PSEA-II[9](Pareto envelope-based selection algorithm II)、NSGA-II[10](Non-dominated sorting genetic algorithm II)等，其基本框架如图2所示。这些进化算法在解决一般低维多目标优化问题(目标数不超过3个)时具有良好的收敛性和分布性，即既能够比较好的逼近真实的帕累托最优前沿面，又能在真实帕累托最优前沿面上分布均匀[7]。

图2 进化算法基本框架

在多目标进化计算中，约束处理是学术界和工程界共同关注的热点研究课题，目前主流的一些智能约束处理技术包括罚函数法、基于多目标的方法和使用元启发式算法等,文献[11]中对这些方法的原理以及优缺点进行了详细的介绍。本文将采用文献[12]中距离量度和自适应惩罚函数相结合的约束处理技术。

2.2 超效率DEA决策模型

以多目标进化计算对供应模型运算所得方案为DMU，即DMU1～DMUn依次代表2.1部分求得的非支配解集所组成的方案集。根据输入指标越小越好，输出指标越大越好的原则，以为供应时间、供应成本为输入，以满足度为输出，建立超效率DEA模型。

在Charnes和Cooper提出的具有非阿基米德无穷小的对偶线性规划模型C2R模型基础上，超效率DEA模型在对第j0个DMU进行效率评价时将DMUj0排除在外，其输入和输出被其他所有决策单元的输入与产出的线性组合代替[13]。除评价效率指数不大于1的约束条件，效率值不再限制于0～1之间而是允许超过1[14]。因此，超效率DEA的C2R评价模型为：

(8)

设ε非阿基米德无穷小变量，且其最优解为λ0，s-0，s+0，θ0，则有[15]：

3 案例分析

3.1 案例描述

在某次西南战役阶段任务中，根据联合作战指挥部门预拟的作战方案，共有3个场站执行任务，预计完成该任务需消耗A、B两种关键四站抢修器材，其中单位数量器材A的质量m1为150 kg，单位数量器材B的质量m2为200 kg。为完成此次任务，由3个中间支援点对四站保障分队进行器材保障，并设立1个后方仓库对各中间支援点进行备件的后续补给，其具体的器材供应信息见表1～5。

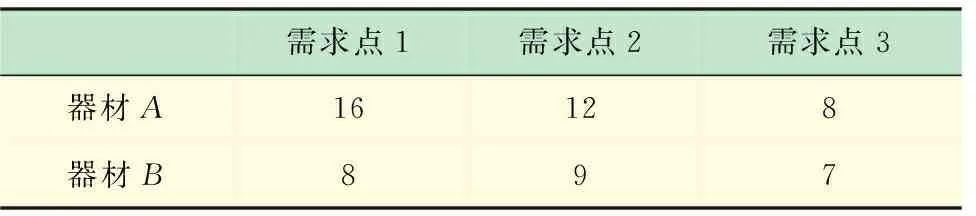
表1 四站保障分队器材需求数量(件)

表2 中间支援点最大运力(kg)

表3 后方仓库向中间支援点供应器材时间(h)

表4 中间支援点向需求点供应器材时间(h)

表5 四站保障分队器材满足率

3.2 求解初始供应方案

根据1.2建立的模型，分别选用MOPSO、NSGA-II、MOEA/D和NSGA-III算法进行求解。为了验证算法的有效性，需要选取一定的指标作为评判标准。MOEA中常用来作为算法性能的评判指标有IGD、SP、HV、RUNTIME等[16]。其中IGD反映了算法的收敛性，SP反映了算法的分布性，RUNTIME反映了算法的计算效率。但是IGD和SP均需要在已知真实帕累托前沿面(pareto front, PF)的前提下使用。而超体积(hypervolume,HV)指标不仅可以同时对解集的收敛性和分布性进行评价，还可以适用于未知真实PF的MOP。，其表达式如下：

(9)

式中:λ为勒贝格测度；xref为参考点。超体积表示帕累托非支配解集所支配的尺寸大小，其值越大，表示算法性能越好。

因此本文采用超体积HV作为算法的评判标准，对比检验不同算法在解决供应模型上的性能，从而选择最优算法的解作为下一步决策的备选方案。MOPSO、NSGA-II、MOEA/D和NSGA-III 4种算法的HV指标如图2所示。

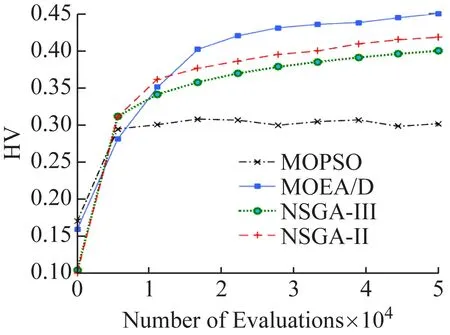
图3 不同进化算法求解时HV指标

通过HV指标可以看出，基于分解的多目标进化算法(MOEA/D)对于四站抢修器材供应多目标问题具有较好的适用性。因此，以MOEA/D算法的解集作为备选方案。由于进化算法的计算结果解集的规模取决于个体规模，通常会产生大量的解。而在这些解中并非所有解均为帕累托最优，所以需要对进化算法求得的方案集进行进一步评估，从而选出较好的方案。选用超效率数据包络分析法(SE-DEA)进一步对方案集进行处理，为决策者做出进一步决策。

3.3 供应方案评估决策

以MOEA/D算法求得的帕累托非支配解集构成初始供应方案，以各个方案为决策单元DMU；后方仓库向各中间支援点，以及各中间支援点向各需求点的供应时间为输入；以各需求点满足率作为输出，建立四站器材应急供应SE-DEA评价模型。以有效的方案作为最终的供应方案。

表6 供应方案SE-DEA评价结果

依据表6，通过对比评价效率θ0的值，可以将决策方案按照评价效率由大到小进行排序。但是，为了给决策者提供灵活的决策空间，通常不仅仅选择效率最大的方案为唯一的最终供应方案。而是将有效的决策变量作为最终的决策方案集。在最终决策方案集中，决策者还可以根据作战实际需要，而将各节点间供应时间以及各需求点的满足率赋予一定的权重，选择符合决策者偏好的供应策略。

4 结 语

本文为解决航空四站保障抢修器材的应急供应决策问题，首先建立了3级供应网络，并用数学模型进行描述，将其转化为多目标优化问题。其次，采用不同的进化算法对其进行求解，并对比了不同算法的性能和效果。最后，对方案集进行评估，从大量的非支配解集中筛选出有效解，大幅缩小了决策规模。结果表明，本文的研究内容可以有效地将智能计算方法和实际问题相结合，为四站器材的应急供应提供了思路，具有一定的学术和军事价值。