基于带符号滑动窗口的ECC抗功耗攻击算法

王 超

(南阳理工学院 软件学院，河南 南阳 473004)

0 引 言

椭圆曲线密码(Ellipse Curve Cryptography, ECC)在安全性相同的情况下，由于与其他公钥密码算法相比具有密钥长度短，处理速度快、存储空间小等优点，使得椭圆曲线密码非常适用于系统级芯片(System on Chip, SoC)等资源受限但安全性需求高的各类系统中[1-2]。但是由Kocher[3]于1998年提出的功耗攻击对基于ECC的SoC芯片带来了极大安全威胁，功耗攻击主要根据SoC芯片中密码算法运算泄露的功耗信息，通过统计分析出功耗和密钥的相关性来获取密钥。在椭圆曲线密码中实施抗功耗攻击最关键的运算是标量乘运算，然而采取抗功耗攻击措施会降低运算效率，但是可以通过对标量采用不同的编码方法来改进运算效率。其中，传统的二进制抗功耗攻击算法是通过添加伪操作来掩盖功耗差异，虽然该算法可以抵抗功耗攻击，但会大幅降低标量乘运算效率。近年来，一些研究人员提出了各种改进算法[4-6]。文献[7]中提出通过将密钥分解成长度相同的多组短密钥，然后在最优组合坐标系下计算标量乘算法，可以保证安全性的情况下有效提升运算效率。文献[8]中提出了一种基于带符号双基数系统的抗功耗攻击方案，该方案主要是利用带符号双基数系统对标量重新编码，同时结合基点掩码技术，以达到保证安全效率和提升运算效率的双重目标。文献[9]中提出了一种基于带符号整数拆分形式的抗功耗攻击方案，该方案通过将标量进行带符号的整数拆分形式编码，并采用基点掩码和标量分割方法实现抗功耗攻击，同时运算效率也有了一定提高。

为解决基于ECC的SoC芯片存在安全和效率之间的矛盾问题，给出了一种基于带符号滑动窗口的ECC抗功耗攻击算法(resisting power attacks algorithm based on Signed Sliding Window for elliptic curve cryptography，SSW)，所给算法主要是利用带符号滑动窗口对ECC标量乘法中的标量进行重新编码，并利用预计算、基点掩码和底层域2kR+S方法，实现了在抗功耗攻击的同时提高标量乘运算的效率，可以很好地解决椭圆曲线密码标量乘算法存在安全与效率矛盾的问题，能够较好地应用在SoC芯片等各类资源受限的系统中。

1 带符号滑动窗口标量乘算法

标量乘运算是椭圆曲线密码中的关键运算，其计算式为：

(1)

式中:Q和P为椭圆曲线上的两个点;k为标量。

经典的标量乘算法一般采用二进制编码的方式，将标量乘运算分解为点加运算和倍点运算。基于二进制编码形式的标量乘运算为：

(2)

式中:n为二进制编码长度，单位为bit;ki为二进制编码系数，且有ki∈{0,1}。下面给出椭圆曲线密码基于二进制编码的标量乘算法:

算法1二进制编码的标量乘算法

输入：k，P；

输出：Q=kP。

(1) 令Q=O；//其中O无穷远点

(2) 对于变量i从n-1到0，则重复执行：

Q=2Q；

如果ki=1，则有Q=Q+P；

(3) 返回Q。

带符号的滑动窗口算法[10]主要是针对标量k的二进制编码，用宽度为w+1的窗口对其进行分组，如果窗口中的最高位是1时，则表示该窗口的值为负数，即此时窗口的值应采用补码表示(窗口中所有二进制位取反，末位加1)，同时需要产生一个进位。则标量k的带符号滑动窗口编码系数是由{-2w+1,…,-3,-1,0,1,3,…,2w-1}中元素组成。文献[11]中给出证明：采用带符号滑动窗口编码可将一个n比特二进制序列转化为具有最少非零个数的编码形式，且其非零位平均个数是n/(w+2)。则有标量k的带符号滑动窗口编码为：

2(2…(2(2·st-1+st-2)+st-3)…+s1)+s0

(3)

式中:sj为标量k的带符号滑动窗口编码;t为标量k的带符号滑动窗口编码长度。其中j∈{0,1,…,t-1}，且有sj∈{-2w+1,…,-3,-1,0,1,3,…,2w+1}。下面给出标量k的带符号滑动窗口编码算法:

输入：正整数k；

输出：(st-1,st-2,…,sj,…s1,s0)。

(1) 对于变量j从0到t-1，则重复执行：

如果sj=0，则执行j=j+1；

如果sj=1，则执行：

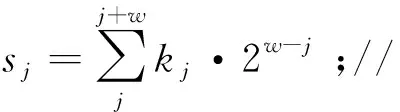
如果sj+w=1，则执行：

对于项目成本的控制，具体实施过程中不能只局限于纸上谈兵，或是以牺牲施工质量和安全为手段来达到降低项目成本的目的。在施工过程中，现场人员要进行现场蹲守，多观察，勤思考，多沟通，随时进行调整，达到创新的目的。应该根据合同要求的工程项目、质量、进度等指标，详细地编制好施工组织设计，作为制定计划成本的基础。对合同中的暂定项目和存在变更的分项工程，要进行严格审核，及时申报，避免返工、窝工以及浪费。

kj+w+1=kj+w+1+1；

对于j从j+1到j+w+1，则有sj=0；

j=j+w+1；

(2) 返回(st-1,st-2,…,sj,…s1,s0)。

根据式(3)标量k的带符号滑动窗口编码，则可得基于带符号滑动窗口的标量乘运算为：

(4)

式中,Pj=sj·P需要通过预计算求出，也即构造一个预计算表{(-2w+1)P,…,-3P,-P,3P,…,(2w-1)P}，可用于主运算执行时查询调用。由此可知，基于带符号滑动窗口的标量乘算法主要分为3个步骤：一是标量k的带符号滑动窗口编码；二是构造预计算表Pj；三是执行主循环运算，求出Q=kP。下面给出基于带符号滑动窗口标量乘算法的具体描述:

算法3基于带符号滑动窗口的标量乘算法

输入：k，P；

输出：Q=kP。

(1) 计算(st-1,st-2,…,sj,…s1,s0)；

(2) 构造预计算表Pj；

(3) 令Q=O；//其中O无穷远点

(4) 对于变量j从t-1到0，重复执行：

Q=2Q；

如果sj>0，则有Q=Q+Pj；

(5) 返回Q。

式中，预计算表Pj的生成方法如算法4所示。

算法4预计算表Pj生成算法

输入：w，P；

输出：预计算表Pj。

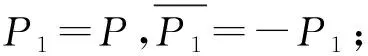
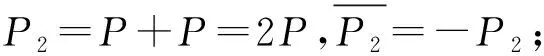
(3) 对于j从1到2w-1-1，则执行：

P2j+1=P2j-1+P2；

(4) 返回Pj。

2 功耗攻击及其防御

功耗攻击根据所采取的攻击手段不同[12]，主要可以分为简单功耗攻击(Simple Power Attack, SPA)与差分功耗攻击(Differential Power Attack, DPA)。其中，针对ECC的功耗攻击主要有零值点功耗攻击(Zero-value Power Attack, ZPA)与修正功耗攻击(Refined Power Attack, RPA)。目前，抵抗功耗攻击的防御措施主要有电路层级与算法层级两类。电路层级的抗功耗攻击措施[13]主要是功耗恒定和功耗互补技术，通过设计无功耗泄露的基本电路单元，或是增加一个互补的电路单元，来构建高安全性的密码模块。算法层级的抗功耗攻击措施包括添加伪操作、随机化密钥和基点掩码等。其中，基点掩码[14]是最为广泛的抗功耗攻击方法，其基本思想主要是通过引入一个或多个随机数与密码算法中生成的中间结果执行一定的算术或逻辑运算，以随机化加密算法中的所有中间结果以及泄露相关的功耗能量信息，实现对SoC芯片内部运算数据的掩盖，使得攻击者无法从外部可探测功耗信息与内部的中间运算数据的相关性，以实现抵抗功耗攻击的目标。

简单功耗攻击是通过测量密码算法的功耗信息来猜测在某时刻对应的运算过程及操作次数，以此判断该时刻所对应的密钥信息。目前抵抗简单功耗攻击的措施主要包括添加伪操作、归一化标量乘法和统一的点加和倍点操作等。

差分功耗攻击是通过测量密码算法的多次功耗曲线，然后对其进行统计分析来获取密钥，不需要考虑密码算法的具体实现细节。目前抵抗差分功耗攻击的措施主要包括随机化密钥、随机化基点、随机化曲线参数和随机化投影坐标等。

零值点功耗攻击是通过测量寄存器为0时所获得的有效功耗曲线，以此来区分标量乘运算中的点加和倍点运算，进而获取密钥信息。目前抵抗零值点功耗攻击的措施主要包括基点掩码和标量分割等。

修正功耗攻击是利用特殊点(x,0)或(0,y)使随机化投影坐标的方法无法起作用，进而可以使攻击者采用DPA攻击以获取密钥。目前抵抗修正功耗攻击的措施主要包括基点掩码和标量分割等。

3 基于SSW抗功耗攻击算法

所给基于SSW抗功耗攻击算法的基本思想是首先利用带符号滑动窗口编码算法对标量进行重新编码，以使编码形式的非零位个数最少；然后引入一个随机点R，用以实现随机盲化基点的目的，并将随机点结合在预计算中生成新的预计算表；最后利用底层域直接计算2kR+S的方法[15]执行标量乘运算，不仅可以归一化点加和倍点操作，同时还可以提高运算效率。下面给出基于SSW抗功耗攻击算法的具体描述过程，主要可以分为如下3个步骤：

步骤1利用算法2求得标量k的带符号滑动窗口编码形式，即:

sj∈{-2w+1,…,-3,-1,0,1,3,…,2w+1}

步骤2引入一个随机点R，令P1=P-R，然后利用算法4求得基点随机盲化后的预计算表Tj。

步骤3采用底层域直接计算2kR+S的方法来执行标量乘法运算，一方面不仅可以提升运算效率，另一方面也可以归一化点加和倍点操作，使得执行标量乘法运算时没有功耗差异。同时值得注意的是，在主运算中令Q=R，用以抵消在预计算中加入随机点的影响，恢复出真实的返回值。

下面给出基于带符号滑动窗口抗功耗攻击算法的具体描述，如算法5所示。

算法5基于带符号滑动窗口抗功耗攻击算法

输入：k，P；

输出：Q=kP。

(1) 计算(st-1,st-2,…,sj,…s1,s0)；

(2) 随机点R=random()；

(3) 构造预计算表Tj；

(4) 令Q=R；

(5) 对于变量j从t-1到0，重复执行：

如果sj>0，则有Q=2jQ+Tj；

(6) 返回Q。

其中，预计算表Tj生成算法的具体描述，如算法6所示。

算法6预计算表Tj生成算法

输入：w，P；

输出：预计算表Tj。

(1) 随机点R=random()；

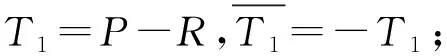
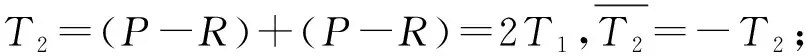
(4) 对于j从1到2w-1-1，则执行：

T2j+1=T2j-1+T2；

(5) 返回Tj。

4 算法性能分析

4.1 安全性分析

在所给算法5的步骤5中，由于采用了底层域直接计算2kR+S，使得在主循环运算中归一化了点加操作和倍点操作，其功耗曲线不会出现明显差异，因此所给基于SSW抗功耗攻击算法可以抵抗简单功耗攻击SPA。

在所给算法5的步骤4中，由于令Q=R，使得在执行主循环运算时掩盖了中间运算结果和功耗之间的差异，使得攻击者无法对所获取的功耗曲线进行统计分析，因此所给基于SSW抗功耗攻击算法可以抵抗差分功耗攻击DPA。

在所给算法5的步骤3中，预计算Tj时引入了一个随机点R，实现了对原始基点进行了盲化，使得在执行步骤5的主循环运算中无法找到特殊点(x,0)或(0,y)，同时也无法测量寄存器为0时的功耗曲线，攻击者无法利用特殊点或零值寄存器来获取有用的功耗曲线，因此所给基于SSW抗功耗攻击算法可以抵抗零值点功耗攻击ZPA和修正功耗攻击RPA。

4.2 运算效率分析

算法5的步骤1中，计算标量k带符号滑动窗口编码的运算量与标量乘的运算量相比可以忽略不计。算法5的步骤3中，构造预计算表Tj需要执行一次倍点运算和2w-1次点加运算，则构造预计算表Tj所需的运算量为DA+2w-1·AA(下标A表示是在仿射坐标下计算)。算法5的步骤5中，主循环运算需要执行n/(w+2)次底层域直接计算2kR+S，则主循环运算所需的运算量为n/(w+2)·DDAJA(下标JA是在雅克比坐标系+仿射坐标系下计算)。其中，A表示点加运算，D表示倍点运算，DDA表示底层域直接计算2kR+S。表1给出了算法5与二进制抗功耗攻击算法和基于密钥分解抗功耗算法的运算量比较。

表1 算法5与其他经典抗功耗攻击算法的运算量比较

通常认为椭圆曲线密码中512bit的密钥是安全的，即n=512。令采用的窗口宽度为4，则有w=3。其中，d表示密钥分段的个数，且取d=4。在仿射坐标系下，AA的计算量为S+2M+I，DA的计算量为2S+2M+I；在雅克比坐标系下，AJ的计算量为4S+12M，DJ的计算量为6S+4M；在仿射坐标系+雅克比坐标系下，AJA的计算量为3S+8M，DDAJA的计算量为(4w+3)S+(4w+9)M[16]，tJ→A的计算量为44M。其中，M表示模乘运算，S表示平方运算，I表示模拟运算，且有I=20M和S≈M。表2给出了算法5与二进制抗功耗攻击算法和基于密钥分解抗功耗算法的运算效率比较。

表2 算法5与其他经典抗功耗攻击算法的运算效率比较

从表2可以看出，所给算法5的总运算效率比二进制抗功耗攻击算法提升了71.47%，比基于密钥分解的抗功耗攻击算法提升了45.46%。同时可以看出，所给算法5所需的预计算运算效率比基于密钥分解抗功耗攻击算法的预计算运算效率提升了97.29%，这表明所给算法5在SoC芯片中占用的存储资源也较少。所以对于SoC芯片等资源受限的各类应用系统，所给算法5更加便捷高效。综上可知，所给基于带符号滑动窗口抗功耗攻击算法不仅可以抵抗SPA、DPA、RPA和ZPA等多种功耗攻击，而且运算效率也得到大幅提升，同时占用存储空间也较小。因此，所给算法5能够同时兼顾安全和效率两方面，可以较好地应用在各类资源受限的系统中。

5 结 语

功耗攻击由于其实现简单和成功率高等优点，使得椭圆曲线密码在抵抗功耗攻击的过程中面临着安全和效率矛盾的问题。标量乘法是椭圆曲线密码中的关键运算，通过进一步对标量进行带符号滑动窗口编码，大大减少了编码中的非零位个数，同时结合预计算、基点掩码和底层域直接计算，从而实现抵抗功耗攻击的目的。与二进制抗功耗攻击算法和基于密钥分解的抗功耗算法相比，所给基于带符号滑动窗口抗功耗攻击算法可以在确保相同的安全性情况下，进一步提升椭圆曲线密码标量乘法运算的效率，可以较好地应用在各类资源受限的系统中，具有较好的理论研究和实际应用价值。