音圈电机一维运动迟滞补偿教学平台

许泽宇， 周之泰， 李英姿， 陈毅夫， 张应旭

(北京航空航天大学 a. 物理科学与核能工程学院； b. 仪器科学与光电工程学院；c. 微纳测控与低维物理教育部重点实验室， 北京 100191)

0 引 言

迟滞现象，指一个系统下一时刻的状态，不仅与系统当下的输入有关，更会因其过去输入过程不同而产生不同的输出结果。换言之，一个系统经过某一输入路径运作后，即使返回与最初状态相同的输入值，输出状态也不能回到其初始。迟滞现象广泛存在于电磁驱动式电机中，音圈电机作为电磁驱动式电机的一种，运动过程存在明显的迟滞现象，该现象会严重降低系统的定位精度，造成运动轨迹的失真，也因此成为高精度控制的一个难点。音圈电机是一种直接将电能转换为机械能的直线电机，具有行程大、响应速度快、输出推力大、输出加速度大等优点，理论上，音圈电机可以实现无穷小分辨率[1-2]。因此，音圈电机在大范围高精度定位领域潜力巨大，受到了越来越广泛的关注，成为了研究的热点[3-10]。

作为一种电磁驱动器，音圈电机的迟滞现象是其固有性质。忽略这一现象对音圈电机进行控制，将导致整个定位系统发生震荡，降低音圈电机的定位精度，尤其当驱动频率较高、驱动范围较大时，迟滞现象导致的定位误差很大。因此，分析音圈电机的输入-输出特性，对理解其迟滞特性，设计合适的控制方法，从而在一定程度上消除其迟滞现象引起的定位误差具有重要意义。

为了描述音圈电机的输入-输出特性，近年来，国内外科学工作者们开展了大量研究工作。埃因霍芬理工大学的 Laurentiu Encica 等[11]和上海交通大学的王曦等[12]分别测量了圆柱型音圈电机和矩型音圈电机的力-位移关系。结果表明，音圈电机在工作过程中，其线圈在不同位置上受到的安培力不同，且当输入电流幅度较大时，音圈电机的推力和输出位移之间存在明显的非线性关系。

目前提出了很多模型用来描述迟滞现象，如Preisach模型[13]，Prandtl-Ishlinskii模型[14]以及Duhem模型[15]，这些模型可以看成是多个迟滞算子的加权叠加结果，其中，由于Prandtl-Ishlinskii模型可以解析反演而得到了广泛的接受和研究。

为了更好地帮助学生理解迟滞现象和迟滞补偿，本文建立了音圈电机一维运动迟滞补偿教学平台，使学生对迟滞特性的建模、求逆及补偿有直观的理解。本文基于搭建的音圈电机一维运动迟滞补偿教学平台，针对音圈电机的迟滞现象，采用广义Prandtl-Ishlinskii模型的表达式和反演算法来实现音圈电机的迟滞补偿。

1 教学平台搭建

为了消除音圈电机的迟滞现象，提高音圈电机的定位精度，从音圈电机的输入-输出特性入手，通过该平台得到其输入-输出数据，并绘制输入-输出特性曲线。选取合适的模型建立音圈电机迟滞模型，准确描述音圈电机的输入-输出特性，通过对该模型的分析和反演，设计音圈电机的控制算法，提高其输入-输出线性度，从而提高音圈电机的定位精度。

教学平台的工作原理图如图1所示。其中：x(t)为所求一维运动位移；u(t)为输入电机的电压；g[u](t)为反馈数据，即包括历史位移等数据的综合；h(t)为进入算法的原始数据；Δ-1[h](t)指代反演算法。由以上原理搭建教学平台如图2所示。

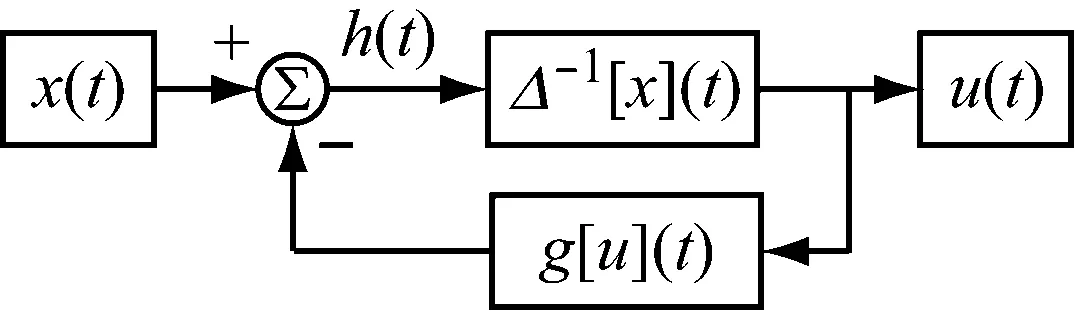
图1 教学平台工作原理图

①-函数信号发生器， ②-直流稳压电源， ③-音圈电机控制器； ④-音圈电机一维运动平台， ⑤-计算机

2 音圈电机迟滞模型的建立

在Matlab中，采用广义Prandtl-Ishlinskii迟滞模型对音圈电机迟滞现象进行建模，采用粒子群算法对待求参数进行识别。

2.1 广义Prandtl-Ishlinskii模型

在广义Prandtl-Ishlinskii迟滞模型中，广义迟滞算子Sr包含两个包络函数，随时间增加的输入函数v对应Sr中的包络函数γl；随时间减小的输入函数v对应广义迟滞算子Sr中的包络函数γr，由于两个包络函数可以为不同的表达式，因此广义Prandtl-Ishlinskii迟滞模型可以描述非对称和饱和的迟滞现象。图3为广义Prandtl-Ishlinskii迟滞模型的迟滞算子的输入输出关系示意图，从图中可以看出，包络函数γl和γr是严格增函数，并且满足γl-r≤γr+r的条件。对于任意v(t)∈Cm[0,T]，广义Prandtl-Ishlinskii迟滞模型的迟滞算子可以表示为

Sr[v](t)=z(ti+1)=

(1)

式中，r是阈值，由经典迟滞算子决定。如图3所示，广义迟滞算子在输出z(t)=0时对应的输入值v(t)为ζ1和ζ2，其中ζ1对应上升阶段，ζ2对应下降阶段，正是因为广义迟滞算子存在不同的ζ1和ζ2，使得广义Prandtl-Ishlinskii迟滞模型可以描述非对称的迟滞回线。其中包络函数γl和γr的表达式为

(2)

式中：a1,b1,c1,d1及a2,b2,c2,d2分别为上升和下降阶段包络函数的待确定参数，由粒子群算法辨识得到。

图3 广义Prandtl-Ishlinskii迟滞算子的输入输出关系示意图

广义Prandtl-Ishlinskii迟滞模型Φ通过多个迟滞算子Sr和密度函数pr(r)的加权叠加来描述相关材料或者驱动器的迟滞效应。广义Prandtl-Ishlinskii迟滞模型的输出具体定义为Φ[v](t)，在映射关系为C[0,T]→C[0,T]的前提下，广义Prandtl-Ishlinskii迟滞模型的表达式为

(3)

式中，η为n个广义Prandtl-Ishlinskii迟滞算子的加权输出结果；P(ri)和ri的表达式分别为

(4)

ρ为常数，τ和α为正数，三者均是迟滞算子模型中的待定参数。

由于广义Prandtl-Ishlinskii迟滞算子为Lipschitz连续，并且加权密度函数为可积的，所以可以得出广义Prandtl-Ishlinskii迟滞模型对于给定的v(t)∈C[0,T]是Lipschitz连续的。因为广义Prandtl-Ishlinskii迟滞算子Sr是单调的，并且密度函数是可积的正值函数，故广义Prandtl-Ishlinskii迟滞模型是单调的运算符。

2.2 粒子群算法

广义Prandtl-Ishlinskii迟滞模型的迟滞算子及密度函数的相关参数通常由已知的实验数据，采用合适的参数识别方法得到，在这里给出粒子群算法[16]，用于模型的参数识别，通过多个粒子向最优解不断逼近，每次取众多粒子中最优的粒子解，最终得到最接近实验数据的拟合参数。粒子群算法的基本过程如下：

(5)

步骤2求每个粒子的适度值。

(6)

(7)

gbest(k+1)=min{pbesti(k+1)}

(8)

步骤3更新每个粒子的速度向量和位置向量

vi(k+1)=w(k)vi(k)+c1r1[pbesti-xi(k)]+

c2r2[gbest-xi(k)]

(9)

xi(k+1)=xi(k)+vi(k+1)

(10)

式中：r1、r2为[0, 1]上随机数；w(k)=0.5+rand/2。

步骤4求各个粒子的适合度，见步骤2。

步骤5计算pbest和gbest，见步骤2。

步骤6若迭代次数大于itermax，终止计算保存gbest作为最优解，否则回到步骤3。

3 音圈电机的迟滞补偿

在Matlab中，对已建立的音圈电机迟滞模型进行反演计算，广义Prandtl-Ishlinskii模型的反演式为

(11)

分别对上升、下降阶段包络函数进行反演，迟滞算子,

(12)

(13)

式中,密度函数求解如下：

(14)

4 教学平台的实验验证

选取音圈电机一个运动周期的数据，采用粒子群算法识别得到参数如下：α=5.201 0,ρ=1.016 3,τ=16.965,a1=9.321 6,b1=1.657 2,c1=1.263 8,d1=-7.645,a2=11.541,b2=1.765 4,c2=-1.419,d2=9.945 0,n=50。得到的模型输出与实验数据的符合程度如图4所示。

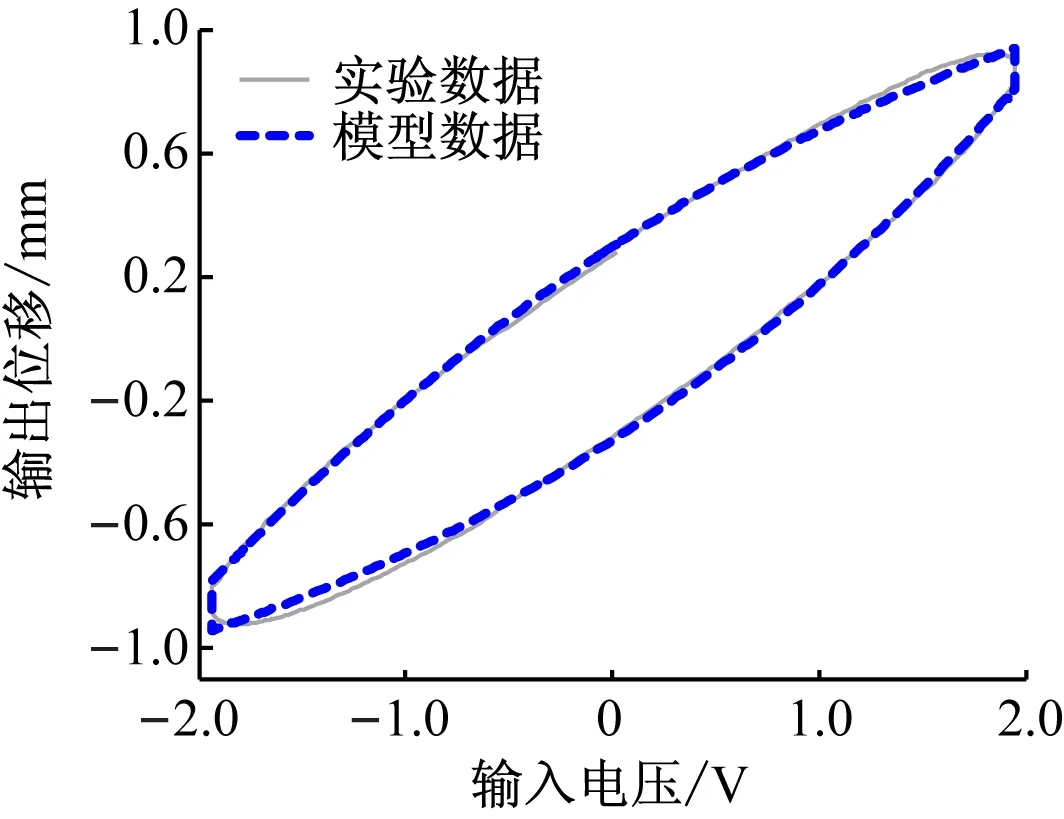
图4 音圈电机迟滞模型与实验数据对比图

相对均方根误差的计算结果为

接着使用Matlab结合反演算法对位移数据进行处理，得到一组输出值，将这组输出值作为新的输入信号输入到音圈电机中，实验得到的实际补偿效果如图5所示。图5中所示输入电压与输出位移曲线的线性度为2.52%。结果表明，广义Prandtl-Ishlinskii模型能够通过解析反演很好地校正迟滞现象。

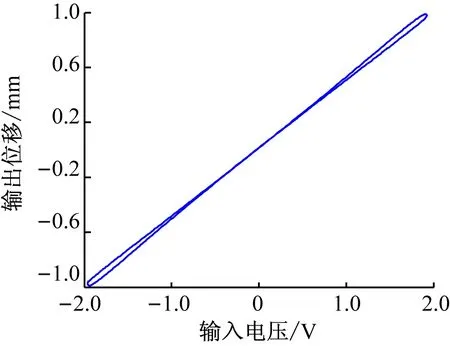
图5 音圈电机迟滞补偿实验结果

5 结 语

本文针对迟滞现象搭建了一套基于音圈电机的一维运动迟滞补偿教学实验平台，该实验采用广义Prandtl-Ishlinskii模型对搭建的音圈电机平台进行建模，并得到其反演模型。通过实验对迟滞现象及其补偿效果进行研究，使得学生对迟滞现象本身、建模及其补偿过程有直观的认识。