基于OMP-SLR的多跳频信号参数估计方法

张 伟，王 宇，乔玉龙，张朝柱

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

0 引言

跳频通信具有优良的抗干扰和多址组网性能，在通信中都得到了广泛应用，在非合作情况下估计跳频信号参数是通信侦察的一项重要研究内容[1-3]。本文主要研究对多个跳频信号的跳时刻、跳频图案等参数进行估计。

文献[4-9]运用时频分析估计跳频信号参数，但时频分析受测不准原理的限制，无法保证估计精度，其中非线性时频还存在交叉项干扰。文献[10-12]提出了一系列基于多维谐波恢复思想的方法，分离并估计出多个跳频信号参数，但是计算量巨大，不适用跳频信号较多和快速跳频的情况。文献[13-14]提出基于自回归滑动平均模型的分析方法，计算简单，但噪声适应能力太差。文献[15-17]提出基于稀疏贝叶斯学习框架的估计方法，但是由于其本身不能保证良好的收敛性能，计算量很大，且估计准确性受到噪声方差估计的严重影响。文献[18-19]提出基于SLR的估计方法，该方法不受测不准原理的限制，可以精确估计跳时和频率，但是需要多次迭代，计算量很大，不适用于大样本点数据。

针对SLR计算量大的缺点，借鉴文献[4,20-21]的思想，提出一种基于OMP-SLR的参数估计方法，该方法在保持SLR精确估计性能的同时，能显著降低计算量。

1 跳频信号稀疏表示模型

假设单通道接收机在观测时间T内接收到K个跳频信号，t时刻接收信号表示为：

(1)

式中，y(t)为接收到的K个跳频信号和噪声的叠加；v(t)为均值为0、方差为σ2的加性高斯白噪声；ak为第k个信号的幅度；fk，t，φk，t，xk，t分别为在t时刻第k个信号的频率、初始相位和复振幅。

将跳频频段网格化为P(P>>K) 点频率集F={f1，f2，…，fP}，使得fk，t∈F，则存在p1，p2，…，pK，使得fk，t=fpk，(k=1，2，…K)。跳频信号可以稀疏表示为：

(2)

式中，

经过周期为Ts的采样信号采样后，稀疏表达式变为：

(3)

式中，ωp为数字角频率；ym为y(t)的第m个采样点y(mTs)；vm为v(t)的第m个采样点v(mTs)。

2 OMP-SLR算法原理

SLR估计精度高，能够精确估计跳变时刻，但是计算量大，算法复杂度是O[(NP)2×L]，且高维信号求逆内存消耗巨大。SLR算法的时间复杂度主要取决于两部分：一是迭代次数L，迭代次数L主要取决于迭代终止条件和迭代步长(迭代步长和罚因子有关，罚因子越大，步长就越大)；二是循环单步迭代，算法复杂度是O[(NP)2](N是信号的点数，P是频率栅格数量)。OMP算法求解速度快，算法复杂度与数据长度呈线性关系O(NP)。

实际中，由于跳频信号在跳变时刻前很长的一段时间是不发生跳变的，如图1所示。很显然，如果将接收信号按时间均匀分为长度为N的若干段，用OMP算法找到跳变所在的段，后对跳变段用SLR精确估计，可以避免对大量的无跳变数据处理所造成的计算花费，大大减少计算量。

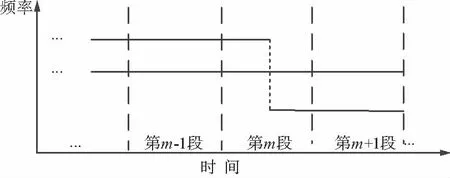
图1 跳频信号时频示意

2.1 OMP原理

OMP属于贪婪类算法，每次迭代过程中，从过完备字典矩阵中寻找一个与信号最匹配的原子，进行最小二乘逼近，并求出信号的残差，然后继续在剩余的原子集合中选择与信号残差最匹配的原子，反复迭代，直到信号残差低于预先设置的阈值或者迭代次数达到预设迭代次数K则停止迭代[22-23]。

在不发生跳变的数据段，该段信号可联合稀疏表示为：

y=[α1，α2，…，αP]×[x1，x2，…，xP]T+v=

Ax+v，

(4)

式中，

y=[y1，y2，…，yN]T∈N×1，

A=[α1，α2，…，αP]∈N×P，

α1，α2，…，αP是由跳频信号频段网格化网格化为P(P>>K)点频率集F={f1，f2，…，fP}后的频率组成的傅里叶基向量，这些傅里叶基向量组成OMP的原子集合，

αp=[ejωp1，ejωp2，…，ejωpN]T∈N×1，(p=1，2，…，P)；x=[x1，x2，…，xP]T∈P×1是系数向量，由于P远大于信号个数K，则x是K稀疏的；v∈N×1是均值为0、方差为σ2的加性高斯白噪声向量。

通过K次迭代，可以从原子集合A中找出与采样信号y最匹配的K个原子，通过这K个原子的矩阵索引值就可以知道这些原子对应的频率。

在发生跳变的数据段m，信号的频率发生了突变，此时该段信号不满足式(5)，但仍可以用OMP算法从原子集合A中找出与采样信号y最匹配的K个原子，只是这K个原子对应的频率不是信号的真实频率。而无论此时估计得到的频率是何值，第m-1和第m段频率不同或者第m和第m+1段频率不同，认为第m段频率估计值相同为正确估计，此时只有两邻的两段是疑似跳变段；其中特殊情况是这连续的3段频率都不同，即第m-1和第m段频率不同，第m和第m+1段频率也不同，认为第m段频率估计值相同为错误估计，此时相邻的3段是疑似跳变段。

经过上述分析可得，发生跳变的段的频率与相邻段的频率会出现不同，可以利用这个规律用OMP定位跳变段的位置。先用OMP分别估计每一段的频率，然后依次后向比较相邻段的频率，找出频率不同的相邻两段，则相邻两段中一定有跳变发生，这相邻两段是疑似跳变段；最后对找出的疑似跳变段分别用SLR算法精确估计出跳时等参数。

2.2 SLR原理

SLR将跳频信号表示为完备傅里叶基之和的形式，对于分段长度为N的采样信号y联合稀疏表示为：

y=Wx+v，

(5)

式中，

y=[y1，y2，…，yN]T∈N×1；

W=[w1，w2…，wN]T∈N×NP，

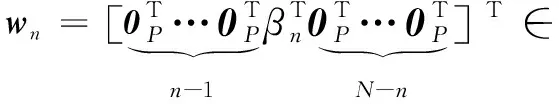
xn=[xn，1，xn，2，…，xn，P]T∈P×1，

xn，p表示n时刻第p个频率的复振幅，xn中元素xn，p大多等于0；v=[v1，v2，…，vN]T∈N×1，vn表示均值为0、方差为σ2的加性高斯白噪声v(t)在n时刻采样值。

利用跳频信号在时域和频域双重稀疏性，将问题建模成带双重约束的稀疏重构问题：

(6)

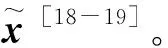
(7)

3 Matlab仿真结果

仿真实验设置2个异步跳频信号的跳频频率范围是3～18.5 MHz，频率间隔0.5 MHz，共32个频率点，采样频率是40 MHz。SLR的乘子参数λ1=0.3，λ2=1.5 ，迭代停止阈值ξ=10-8。

3.1 设置分段长度

无跳变情况下，OMP频率正确估计概率与分段长度和信噪比(SNR)有关，仿真设置频率在频率集中随机选取，仿真结果如图2所示。

图2 无跳变时，OMP频率估计概率

从图2可以看出，分段长度不低于60时，能够在低信噪比下取得非常满意的估计效果。

SLR跳时正确估计概率与数据长度有关，数据越多，则提供的信息越多，算法正确估计跳时的概率越高。仿真设置跳变位置在段中间，仿真结果如图3所示。

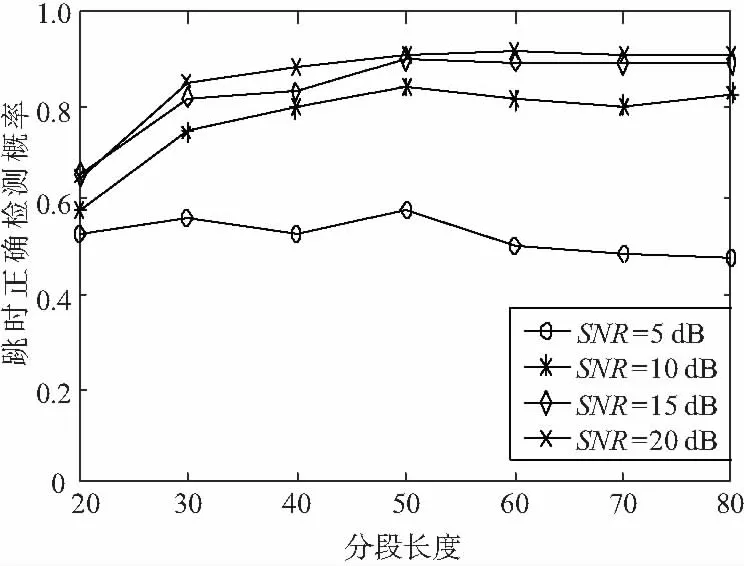
图3 SLR跳时估计概率

从图3可以看出，随着段长度的增加，SLR跳时估计概率总体呈现缓慢增大趋势，但是数据越多，时间复杂度越高。综合考虑，在不显著影响SLR估计概率的情况下，本文取段长度为60较为合适。

第m段有跳变发生时。OMP频率正确估计概率与跳变点在数据段的位置及SNR有关，Matlab仿真结果如图4所示。

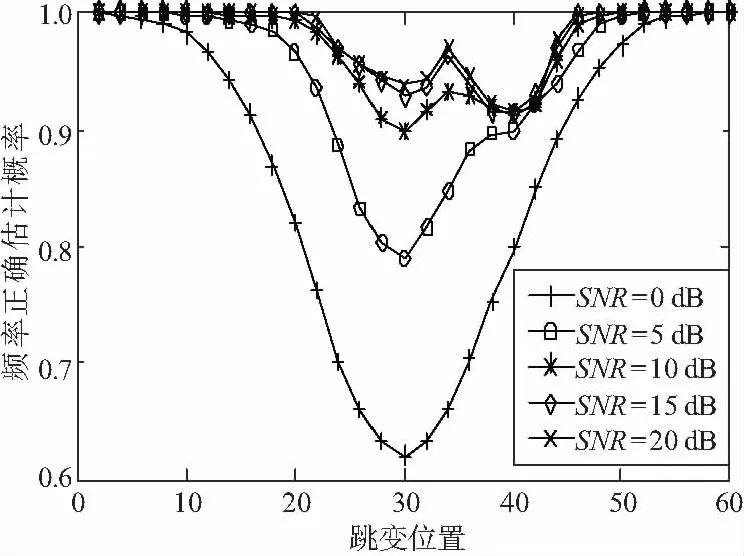
图4 有跳变时，OMP频率估计概率

从图4可以看出，当跳变点在段中间时，该信号与傅里叶基矩阵中单一原子的相似度最小，通过OMP估计得到的正确概率最小。无论跳变点在数据段何处位置，OMP仍能以一定的高概率估计出该跳变段的频率，错误估计概率很小，故疑似跳变段段数的期望值略大于2。

3.2 实例仿真

由OMP-SLR方法可以估计得到跳时、跳周期、跳频图案等，如图5所示。

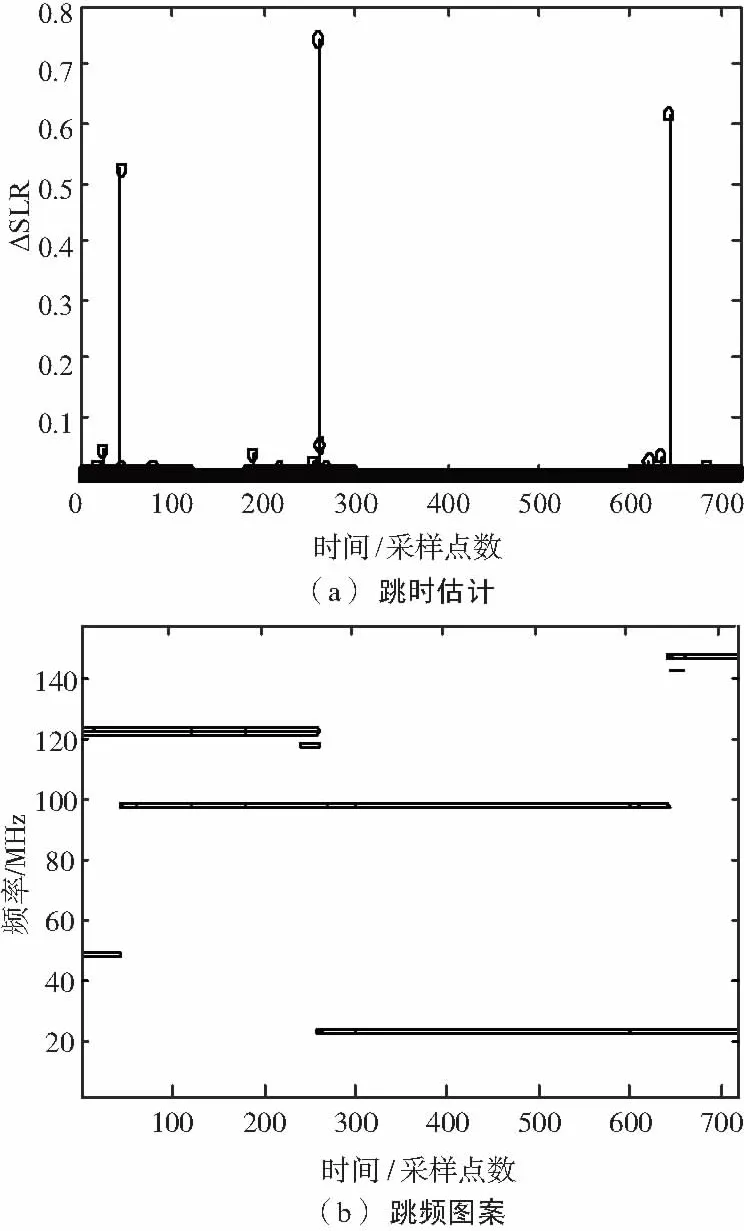
图5 本文算法得到的跳时估计、跳频图案

为计算机仿真方便性考虑，仿真实验设置跳频速率为66 666.7 hop/s，每一个跳频周期内包含600个采样点，信噪比SNR=10 dB。第1个信号在[1，43]采样点区间的频率是7.5 MHz，在[44，643]区间的频率是12.5 MHz，在[643，720]区间的频率是17.5 MHz；第2个信号在[1，260]采样点区间的频率是15 MHz，在[260，720]区间的频率是5 MHz。

3.3 Matlab仿真耗时对比

通过Matlab仿真耗时对比进行验证，结果如表1所示。

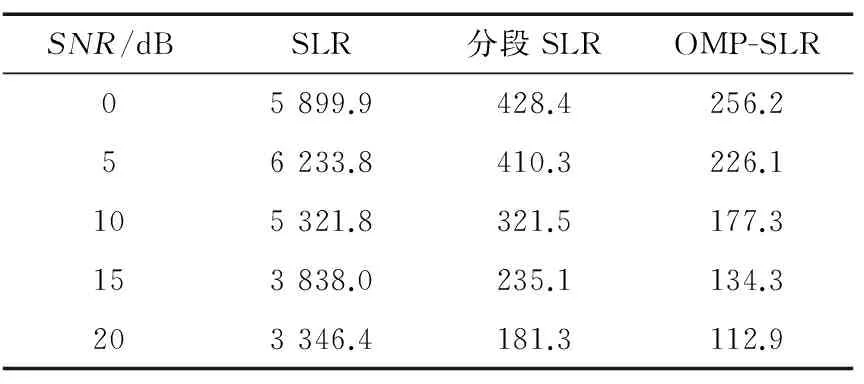
表1 Matlab运行时间 (s)

分段SLR的段长度也是60。从表1可以看出，本文提出的OMP-SLR算法能显著减少计算量。现有高速跳频信号跳速一般不超过20 000 hop/s，远低于本文仿真设置的跳速率66 666.7 hop/s，跳频速率越低则跳周期越大，分段后不发生跳变的信号段数比例越大，本文方法减少计算量的效果越显著。

4 结束语

针对多跳频信号参数估计方法SLR计算量大的缺点，本文在SLR方法的基础上，将OMP方法引入到SLR方中，提出了一种基于OMP-SLR的多跳频信号参数估计方法。通过对算法的时间复杂度进行理论分析，论证了本文方法的可行性。Matlab仿真结果表明，通过设置合适的分段长度，本文提出的OMP-SLR方法在不显著减少原SLR方法参数估计性能的情况下，显著减少了计算量，跳速越低效果越显著，验证了本文方法的有效性。

本文方法假设信号频率都在频段划分网格点上，对于因频段网格划分不准确或者多普勒频移造成接收到的跳频信号频率不在网格点上的情况还有待深入研究[24]。