星载SAR天线高稳定度指标分配方法研究

范 亮， 高晶波， 王 聪

(哈尔滨工业大学 航天学院 飞行器动力与控制研究所，哈尔滨 150001)

合成孔径雷达SAR(Synthetic Aperture Radar)是一种利用多普勒效应和脉冲压缩技术实现高分辨率成像的雷达[1]。星载合成孔径雷达由于不受天气、气候的影响，能全天时、全天候、高分辨率、大区域对地观测，已经成为空间对地观测的重要手段[2-3]。现如今，SAR卫星天线正朝着多工作模式切换、高分辨率成像的趋势发展[4]。

然而，在SAR卫星天线对地动中成像的过程中：一方面由于卫星天线复杂的工作环境会对天线的指向精度产生影响；另一方面，航天器上的各种有效载荷及调姿扰动等也会对天线动中成像的质量产生影响。因此，研究影响天线指向精度的扰动因素，并对指向精度进行合理分配变得十分必要。

在指向精度影响因素及指标分配研究方面，国内外学者做了许多工作。Kistosturian[5]分析了天线系统误差源并通过在轨校正提高了天线的指向精度。Gawronski等[6]建立了方位—俯仰型卫星天线指向模型，并通过在轨校正补偿了静态指向误差。Ayumu等[7]等分析大型可展天线的指向误差，并采用一种新方法来计算天线的指向稳定度。黄岩等[8]通过成对回波和多普勒中心频率误差来分析天线的指向稳定度对天线成像质量的影响，游斌弟等[9-11]研究了天线柔性，温度场与结构位移场耦合对星载天线动态指向精度的影响，黄龙[12]研究了大型望远镜的指向精度。但国内外很少有文献对星载SAR天线的高稳定度指标分配进行研究。

本文首先根据SAR卫星天线在轨运行的实际环境设计了三种仿真工况，主要包括：CMG(Control Moment Gyro)(控制力矩陀螺)调姿扰动、隔振器、SADA(Solar Array Drive Assembly)(太阳帆驱动机构)扰动，运用ADAMS(Automatic Dynamic Analysis of Mechanical Systems)对SAR卫星天线进行多体动力学分析，以概率法分析影响天线指向精度的指标并进行合理分配，从而为卫星总体选择合适型号的调姿机构提供技术支持。

1 天线的指向精度

1.1 指向精度定义

指向精度可以从指向精度误差和指向稳定度误差两个方面来定义。

指向精度误差：在一段时间内，天线实际指向扰动的均值偏离理想指向的误差值。设理想指向为零均值，指向扰动函数为P(t)，起始时间为t1，时间间隔为T，则指向精度误差可以表示为[13]

(1)

指向稳定度误差：在[t1,t1+T]时间段内连续变化的指向扰动函数与指向均值之差随时间的变化量，可以理解为发生在指向方向上的抖动。其数学表述形式为

P(t,t1,T)=P(t)-Pa(t1,T)

(2)

1.2 指向精度计算

理想天线馈源的相位中心与抛物面的焦点重合。当天线结构受到外载荷作用时，抛物面天线的焦点会与馈源的相位中心发生偏离，这一变化过程如图1所示。

抛物面天线的焦距记为F，当天线的焦点由A偏移至B时，二者的偏距记为ΔF，产生的偏移角记为θ1，则有[14]

θ1=arctg(ΔF/F)

(3)

横向偏移ΔF在X，Y平面内的投影量为

(4)

(5)

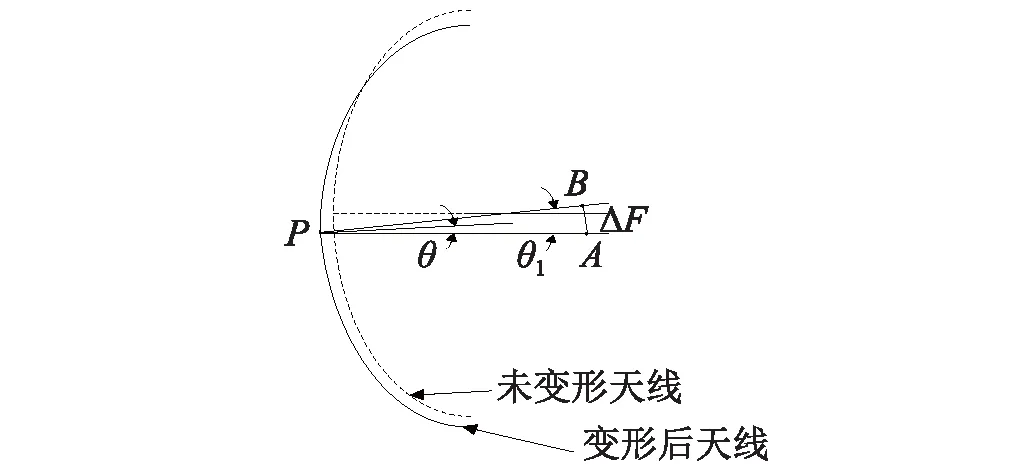
图1 天线结构变形图Fig.1 Antenna structure deformation

由θ1引起的波束方向相对原轴线的偏移角θ为

θ=Kθ1

(6)

式中：K为波束因子，由于本文中天线的焦径比为0.24，查找相关资料可知K取0.75。

如果天线的结构变形在同一个平面内，可按照上述方法计算。若实际波束指向偏移角在不同平面内，则可分别计算抛物面在两个平面内的变形，此时，天线的指向精度可表示为[15]

(7)

式中：r1为理想位置矢量记为PA(0,1,0)；变形后的位置矢量r2表示为PB。

2 多体动力学仿真

2.1 有限元模型

SAR卫星由星本体、天线、馈源和帆板组成。天线与星本体分别采用刚性和柔性两种连接方式。其中，星本体的主承力柱采用实体单元，四周面板采用壳单元，帆板结构采用壳单元，框架采用梁单元，天线肋板采用壳单元，绳索采用弹簧阻尼单元等效，帆板与星本体之间采用多点约束连接，建立SAR卫星有限元模型。

在自由状态下，计算整星模型的各阶固有频率并分析其模态特征，结果如表1所示。

整星均为柔性结构，其前六阶模态为刚体模态，整星各个附件的一阶模态特征如图2所示。太阳帆的固有模态出现在整星的第七阶，其固有频率为0.716 Hz，如图2(a)所示。天线的固有模态出现在整星的第十一阶模态，其固有频率为0.924 1 Hz，如图2(b)所示。馈源的固有模态出现在整星的第十三阶，其固有频率为1.977 Hz，如图2(c)所示。

表1 整星有限元模型固有频率和模态特征

图2 整星的重要模态Fig.2 Important modal of the SAR satellite

2.2 多体动力学仿真

当SAR卫星在轨运行的过程中，主要采用条带模式与扫描模式，在天线对地的动中成像过程采用聚束模式及滑动聚束模式，整个天线在轨运行的过程是一个多模式切换的过程。

由于天线在轨运行工作环境的复杂性，影响天线指向精度的因素众多，本文主要分析影响其指向精度的振源扰动，包括：隔振器扰动、CMG调姿扰动(力、力矩)、SADA扰动。

按照卫星天线动中成像的实际运行过程，分别研究单一载荷加载对天线指向精度的影响，便于对各扰动因素对指向精度的影响程度进行分析。因此，设计三种工况，如表2所示。

表2 三种仿真工况

三种工况的扰动函数均采用零均值，单位方差的输入，如图3所示。分别计算天线结构的变形量及馈源的变形量，然后拟合抛物面焦点和馈源的相位中心，计算天线的指向精度，具体的流程如图4所示。

图3 零均值、单位方差扰动函数曲线Fig.3 Zero mean and unit variance perturbation function curve

2.3 仿真算例

以工况三为例，在SAR卫星的太阳帆上施加SADA扰动，具体的扰动函数如图4所示。然后设置SAR卫星的调姿函数。为简化处理卫星天线多模式切换的复杂过程，将卫星姿态的调整方式设定为沿其Y轴转动。具体调姿的方式如下：卫星沿方位向(X向)从0°～90°定轴转动，转动的角速度为1.5 °/s，并在0～3 s与60～63 s为加、减速阶段，加速度大小为0.5 m/s2，得到调姿曲线如图5所示。

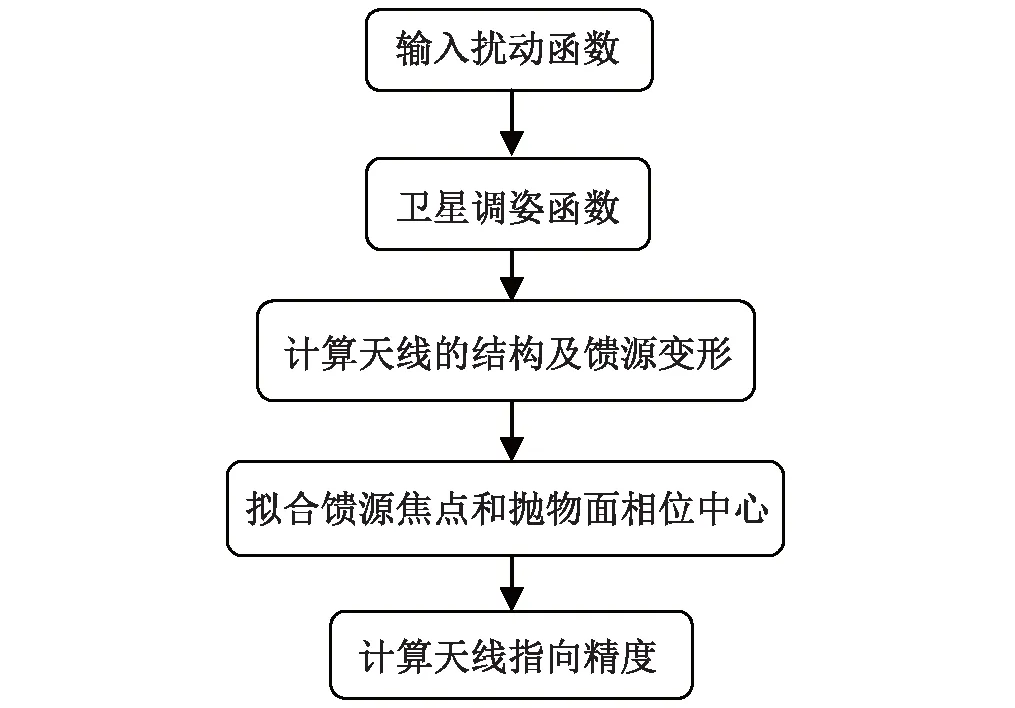
图4 指向精度计算流程图Fig.4 Pointing accuracy calculation flow chart

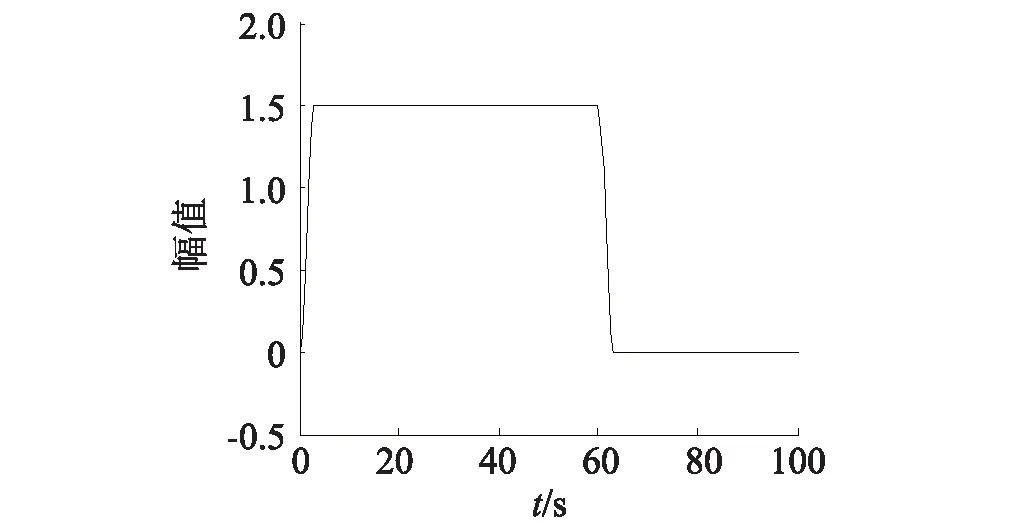
图5 调姿函数曲线Fig.5 Adjustment function curve

然后，选取天线模型对称环肋上的100个标记点来计算天线结构的变形量，其结果如图6(a)～图6(c)所示，同时计算馈源的变形量，其结果如图7(a)～图7(c)所示。

根据天线及馈源的变形量，拟合馈源的相位中心和抛物面的焦点，并计算天线的指向精度，可以得到指向精度在三个方向的变化数量级在10-5mm，SADA单一扰动下的响应满足天线对指向精度的要求，结果如图8(a)～图8(c)所示。

图6 天线结构的变形Fig.6 The deformation of the antenna structure

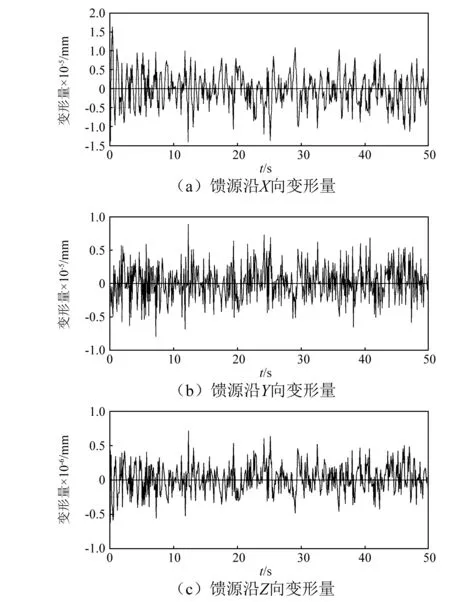
图7 天线馈源结构的变形Fig.7 The deformation of the antenna feed

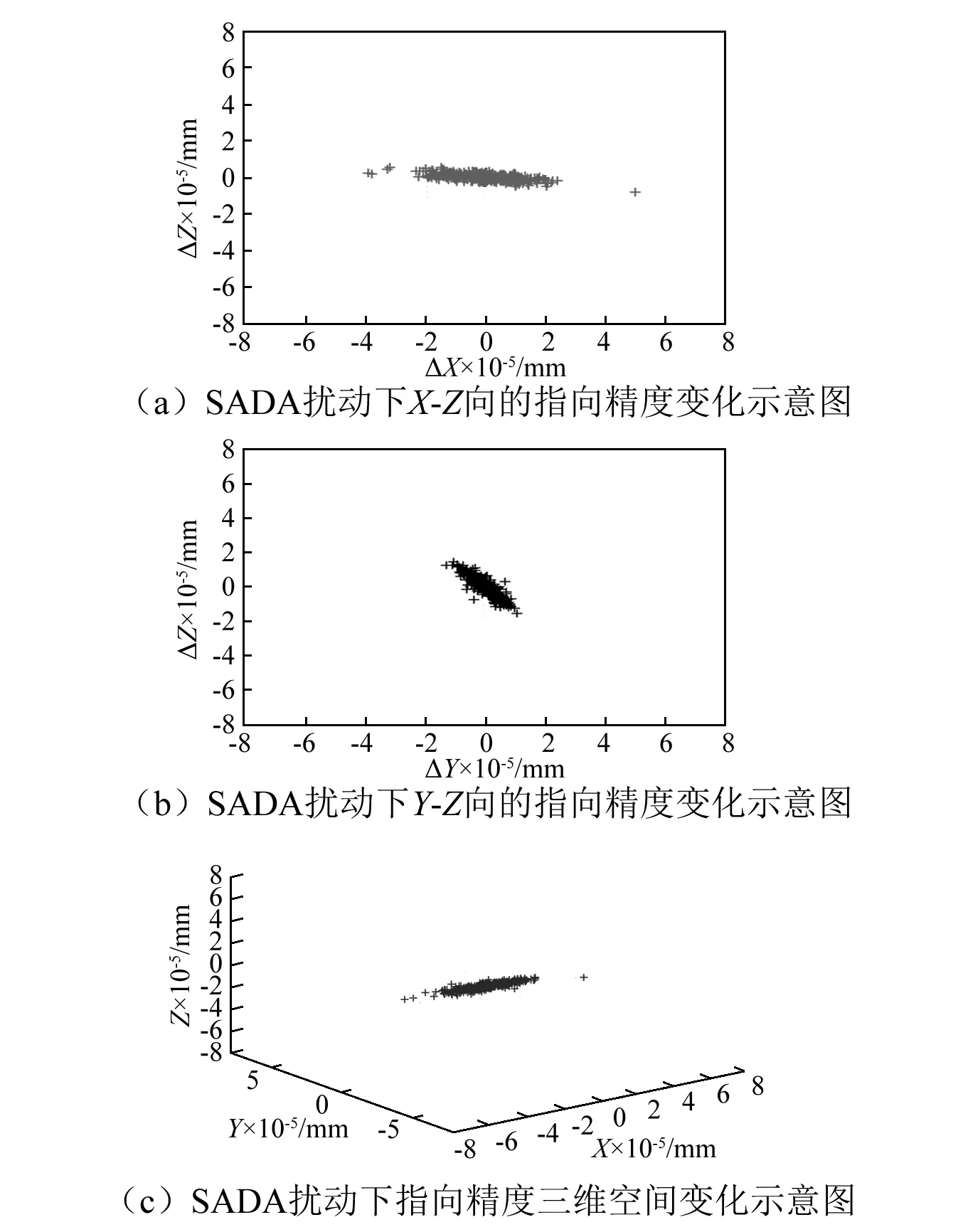
图8 SADA扰动下的天线指向精度的变化Fig.8 Pointing accuracy of the antenna under SADA disturbance

3 高稳定度指标分配

3.1 指标分配方法

根据上述工况，考虑隔振器扰动、CMG调姿扰动、SADA扰动对天线指向精度的影响，用概率法[16]对各项扰动产生的误差进行分配。

系统的总误差为

(8)

式中：a1， ...，an为各项误差的灵敏度；σ1， ...，σn为各项误差的均方根(Root Mean Square, RMS)值。

假设各单项误差服从零均值正态分布或均匀分布，则单位均方差引起的指向误差即为误差灵敏度，其计算公式[17-18]为

(9)

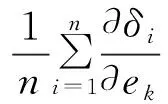
3.2 指标分配步骤

按照上述的系统总误差的计算公式，可将星载SAR天线的高稳定度指标分配归结为以下几个步骤：

步骤1根据选取的影响天线指向精度的扰动源，首先研究单一扰动源对星载SAR天线指向精度的影响。设置各项单一扰动源的输入载荷服从零均值、单位方差分布，并计算在单一扰动下天线结构的变形，拟合天线的相位中心，计算天线的指向精度及单项扰动源对天线指向精度的误差敏感度，从而获得单一扰动源对星载SAR天线指向精度的影响程度。

步骤2根据第一步中计算得到的各项扰动源对指向精度的误差敏感度，进行系统总指向误差的合成，确保星载SAR天线系统总体的指向精度在允许的范围内。

步骤3在满足星载SAR天线系统总体指向误差的条件下，对于各项具体扰动源对指向精度的误差敏感度可以根据选择的工况及部分结构的精度要求进行调整，并留出满足条件的阈值，便于进一步控制及优化各项影响因子，从而提高天线的指向精度及成像质量。

3.3 指标分配算例

在SAR卫星天线对地成像的总指向精度满足高分辨成像的要求下，下面进行各项指标的分配。

以CMG调姿扰动为例进行天线指向精度误差敏感度的计算。本文所采用的六个CMG的具体安装位置及加载方向，如图9所示。在每一个CMG位置处，分别施加服从于σ(0,1)分布的并沿X，Y，Z方向的三个力Fx，Fy，Fz和三个力矩Mx，My，Mz，将它们分别沿平行于五棱锥侧棱的轴向和垂直于侧棱的轴向进行加载，然后计算天线动中成像过程中三个方向转角的误差灵敏度，得到天线三个方向(包括方位向θx、距离向θy、俯仰向θz)的误差敏感度，然后进行指向精度的分配。

图9 CMG加载示意图Fig.9 Diagram of the CMG load

以CMG1为例，按照CMG布置图，在g1位置处分别施加服从于σ(0,1)分布的三个方向的扰动力，计算天线指向精度的误差灵敏度，得到结果如图10(a)所示。

根据上述柱状图分析可知，当仅有CMG1工作的情况下，在输入的扰动力分别为Fx，Fy，Fz时，Fx对指向精度的误差敏感度最大，其均值大于0.6，Fz对指向精度的误差敏感度最小，其均值小于0.1；在单一方向力作用下，Z轴的转角θz的误差敏感度最大，且在Fx单独作用的条件下，θz的误差敏感度数值为1，其值要显著大于对X，Y方向的转角θx，θy的误差敏感度。

同理，仍以CMG1为例，在g1位置处分别施加服从于σ(0,1)分布的三个方向的扰动力矩，计算天线指向精度的误差灵敏度,得到结果如图10(b)所示。

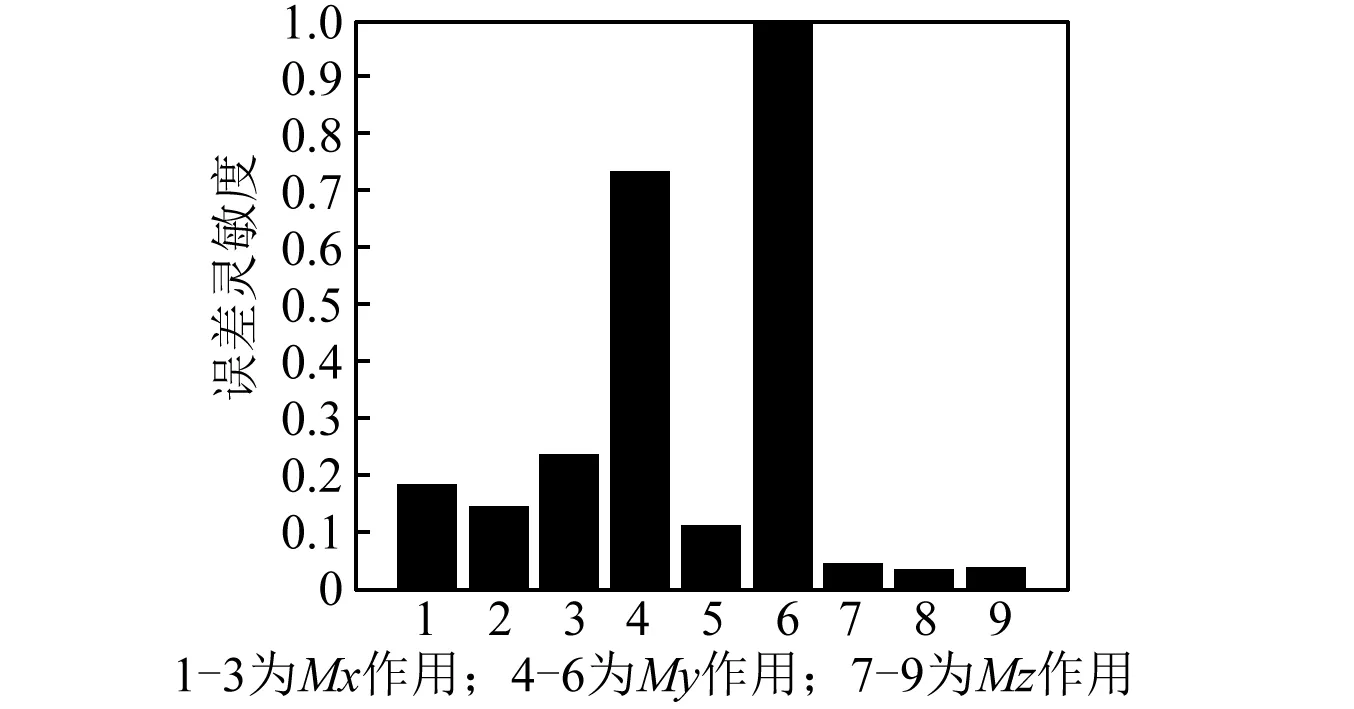
(b) CMG1扰动力矩对天线三个方向转角的误差敏感度图10 CMG1扰动下的天线三个方向转角的误差敏感度Fig.10 Error sensitivities to antenna in three direction angles under CMG1 disturbance

根据上述柱状图分析可知，当仅有CMG1工作的情况下，在输入的扰动力矩分别为Mx，My，Mz时，My对指向精度的误差敏感度最大，其均值大于0.6，Mz对指向精度的误差敏感度最小，其均值小于0.05；在单一方向力矩作用下，Z轴的转角θz的误差敏感度最大，且在My单独作用的条件下，θz的误差敏感度数值为1，其值要显著大于对X，Y方向的转角θx，θy的误差敏感度。

3.4 指标分配结果

按照上述过程，分别对其它五个控制力矩陀螺进行分析，可得各单一方向扰动作用下CMG对天线指向精度误差的影响，结果如图11所示。并同时计算CMG对天线指向稳定度误差的影响，结果如图12所示。

按照CMG调姿扰动分析过程分别对隔振器扰动及SADA扰动进行计算，可得到两种工况对天线指向精度的影响，结果如图13所示。

综合上述三种工况，分别计算三种工况对天线指向精度的影响。由于工况三的误差灵敏度数值要远大于前两种工况，故前面两种工况的数值不明显，将三种工况结果汇总，如图14所示。

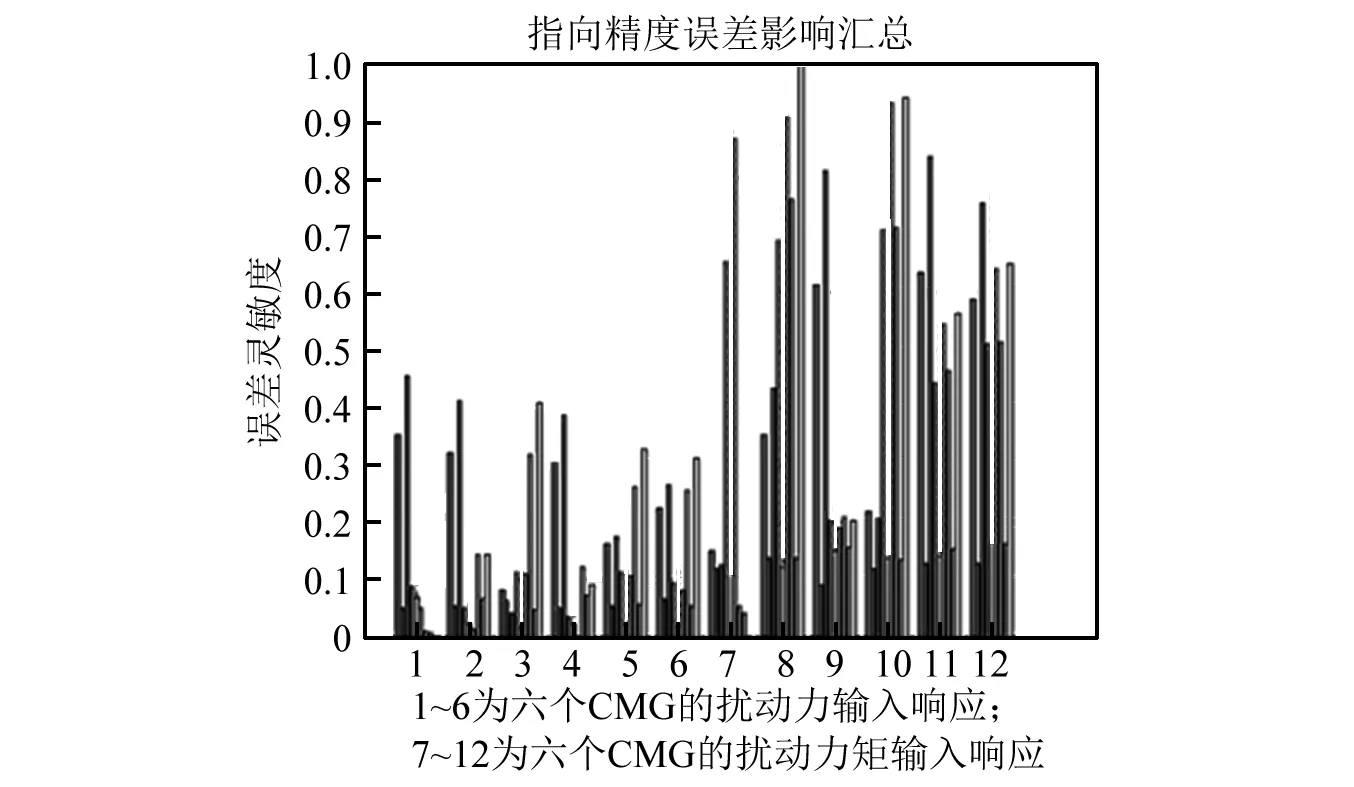
图11 CMG调姿扰动对指向精度误差的影响Fig.11 Influence of CMG perturbation on pointing precision error

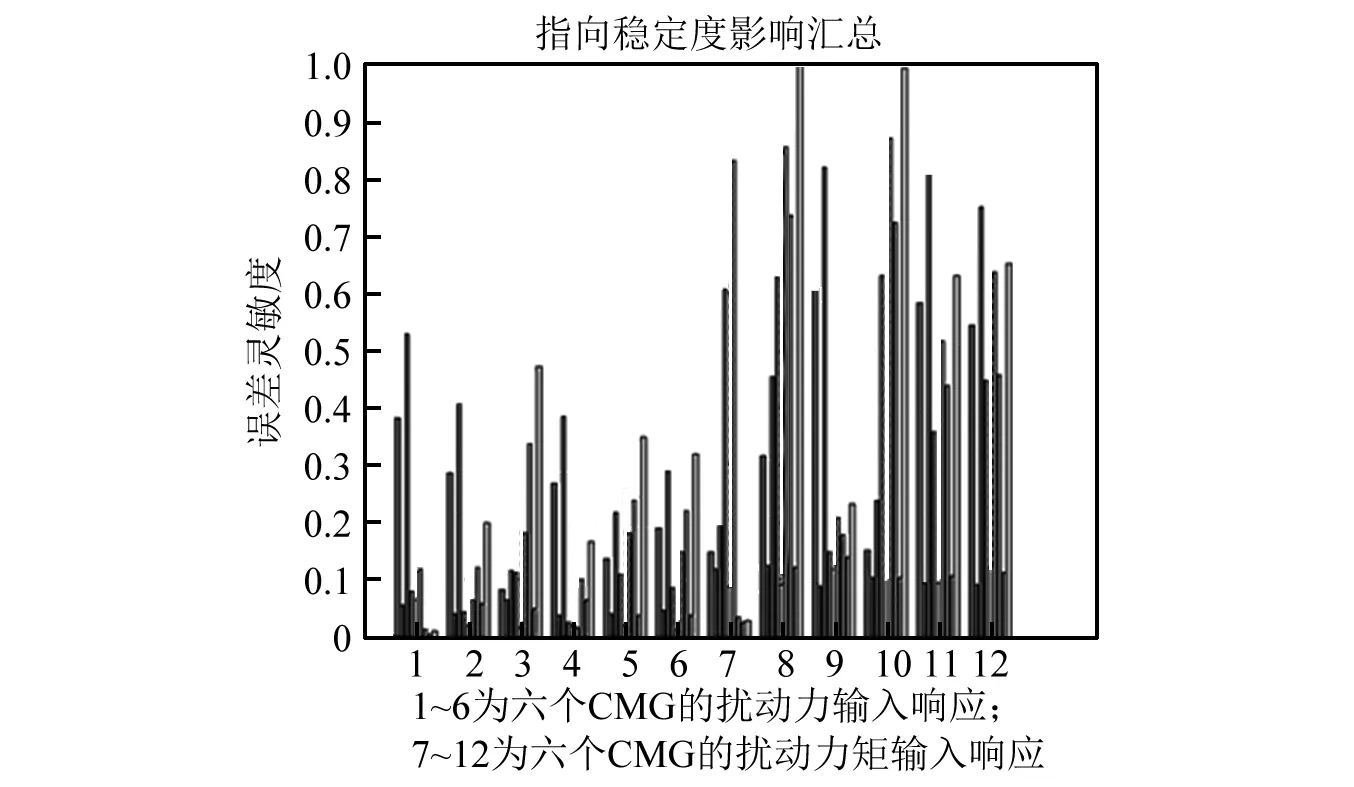
图12 CMG调姿扰动对指向稳定度的影响Fig.12 Influence of CMG perturbation on pointing stabilization

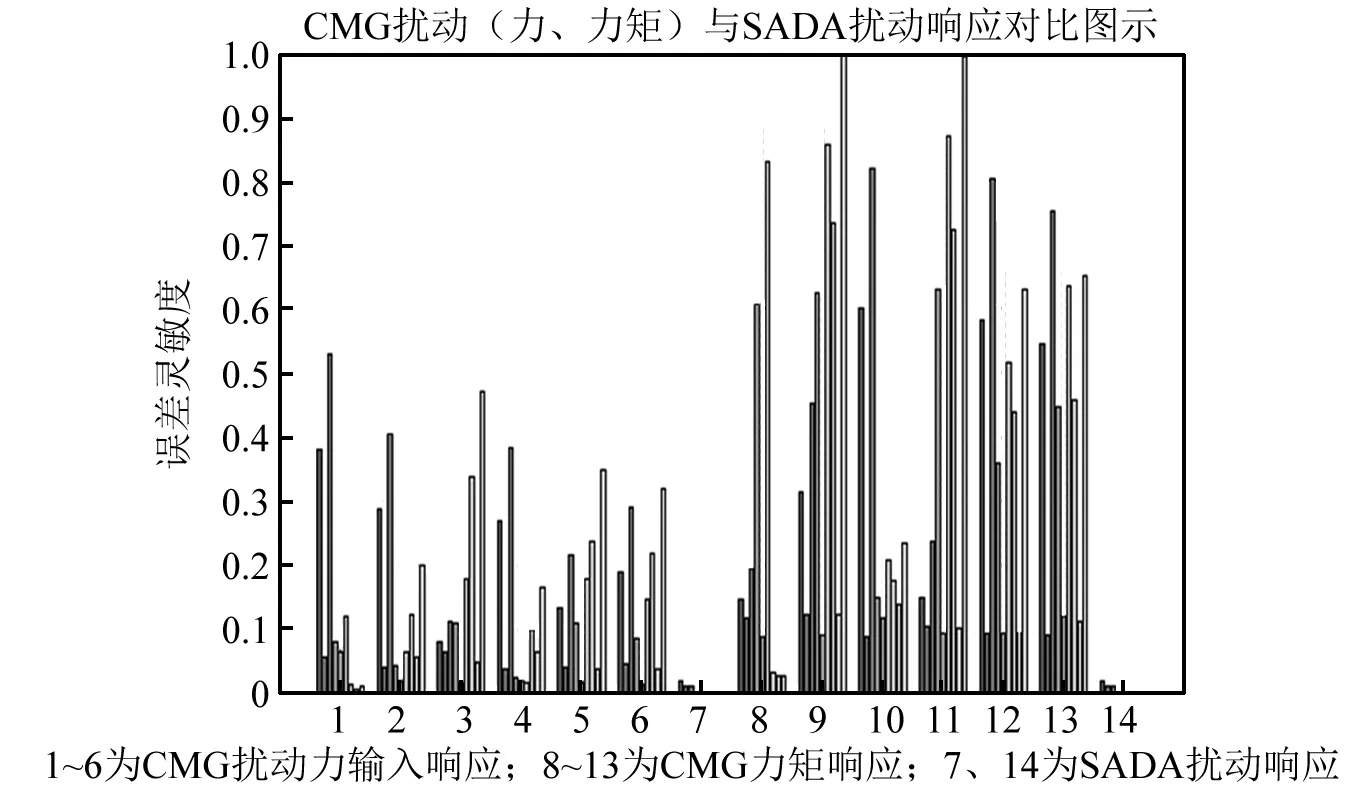
图13 工况二、三对天线指向精度的影响Fig.13 Influences of case two and three on pointing accuracy

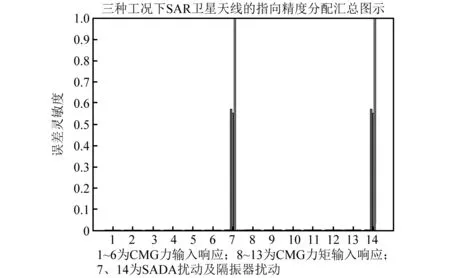
图14 三种工况汇总图示Fig.14 Summary of three conditions

在星载SAR天线系统动中成像的过程中，精调机构可视为隔振器，起到降低星载天线响应的作用，故此时考虑的系统内部的扰动源仅有CMG扰动、SADA扰动，以这两种扰动源为例进行高稳定度指标分配。当分别考虑CMG扰动、SADA扰动在零均值、单位方差扰动源输入条件下，计算天线方位向、距离向、俯仰向三个方向的误差敏感度，其结果如图15所示。

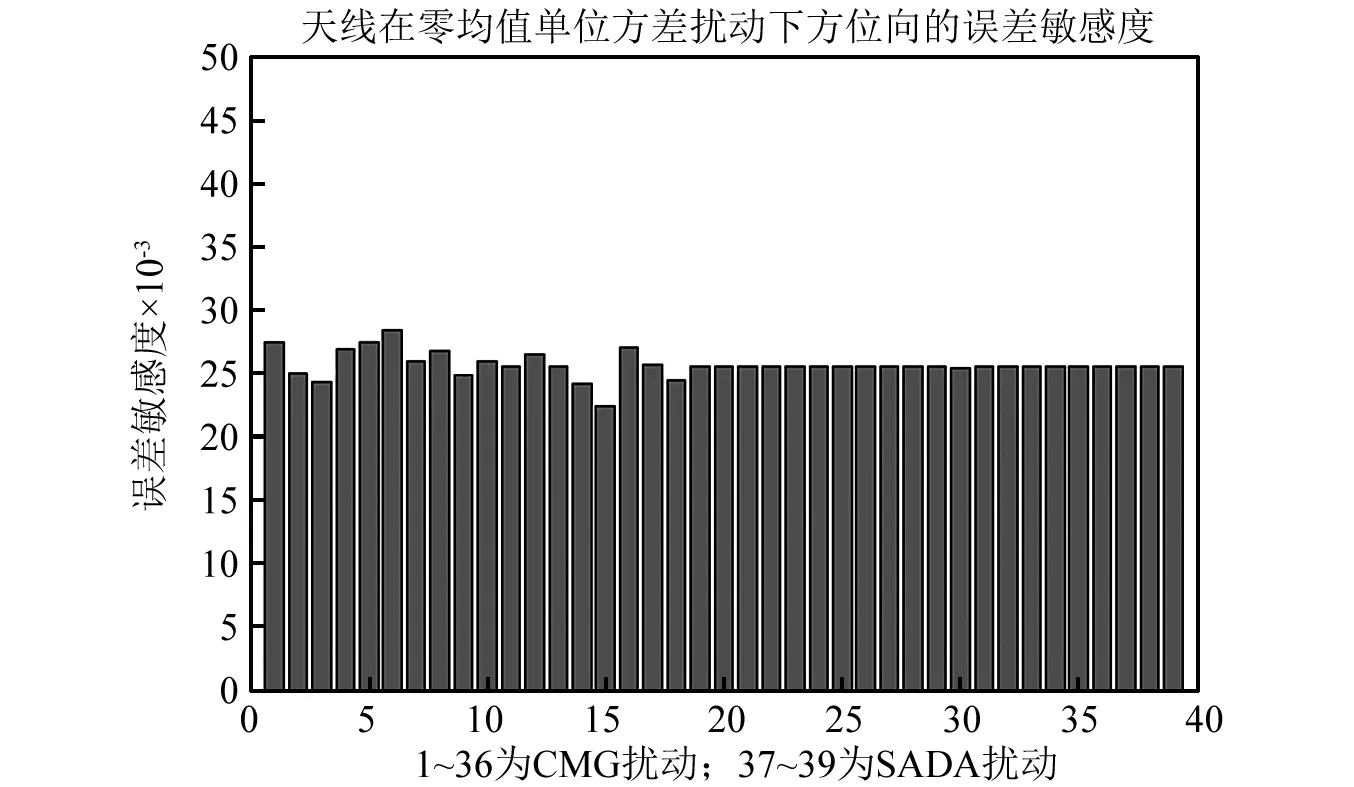
(a) 天线方位向在零均值单位方差扰动下的误差敏感度

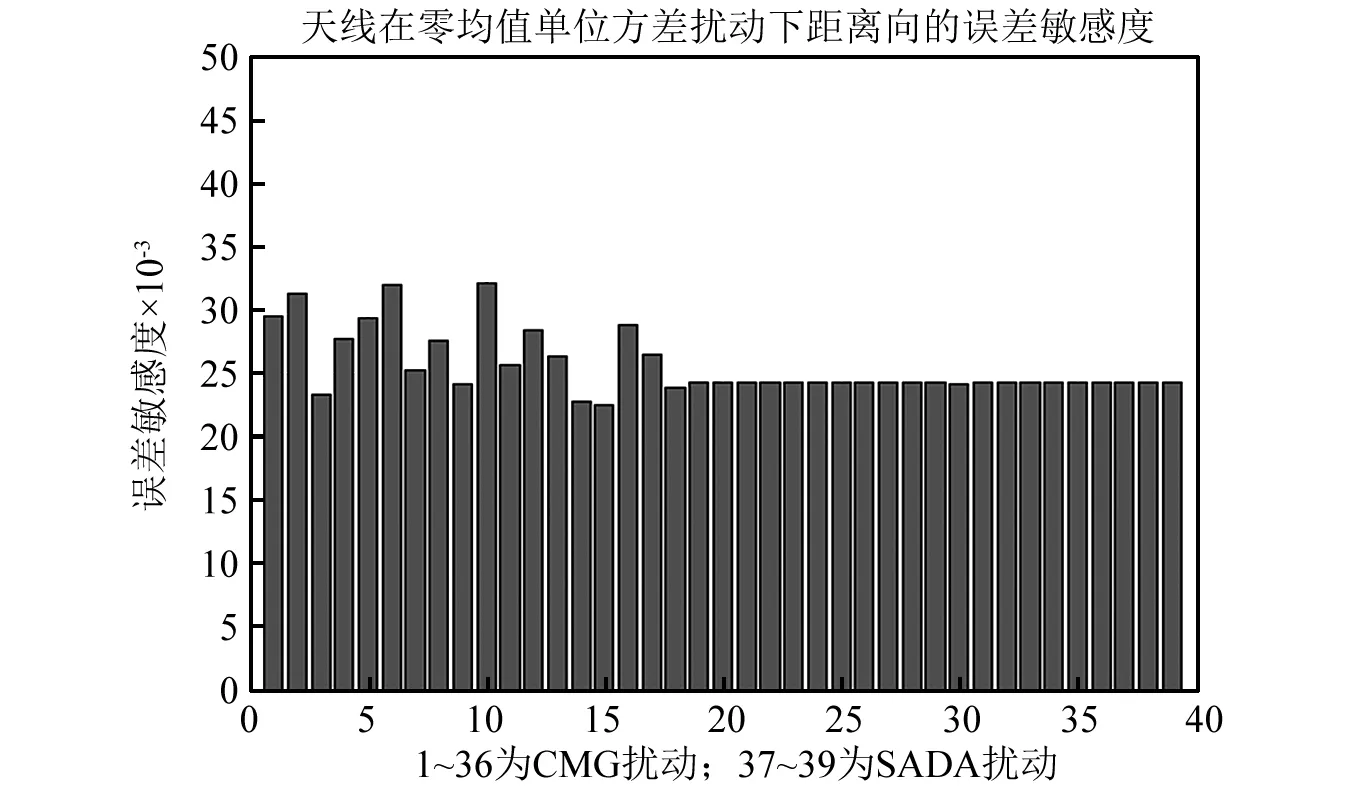
(b) 天线距离向在零均值单位方差扰动下的误差敏感度

(c) 天线俯仰向在零均值单位方差扰动下的误差敏感度图15 天线在零均值单位方差扰动下的误差敏感度Fig.15 Error tolerances of antenna under disturbance subject to zero mean unit variance

根据上述得到的天线三个方向转角对星载SAR天线指向精度的误差敏感度数值，可以对各项扰动源进行合理分配。

4 结 论

(1)由图11的数据可得到，在单一力矩作用下，CMG对卫星天线指向精度的误差敏感度的影响程度要显著大于在单一力作用下的误差敏感度。

(2)比较图11、图13可得，在单一载荷(包括力、力矩)作用时，从广义规律来讲，忽略个别产生的很小误差灵敏度的数值，可以得到CMG对天线三个方向指向精度的误差敏感度的影响顺序由大到小依次为：θz(俯仰角)、θx(方位角)、θy(距离角)。

(3)比较图11、图13、图14可得，三种工况对天线指向精度误差及指向稳定度的影响保持一致，且影响程度从大到小依次为：隔振器的姿态扰动、CMG调姿扰动、SADA调姿扰动。

综上所述，当SAR卫星天线在动中成像的过程中，要提高隔振器的隔振性能，减少有效载荷的扰动对卫星天线指向精度的影响，并在多种模式切换的过程中加强对俯仰角的控制，可以有效提高SAR卫星天线的成像质量。同时，根据计算得到的天线指向精度及误差敏感度，可为卫星总体选择满足总指向精度要求的控制力矩陀螺及太阳帆驱动机构等调姿机构提供帮助。