基于范数归一化和稀疏正则化约束的结构损伤检测

骆紫薇， 余 岭，2， 刘焕林， 潘楚东

(1.暨南大学 力学与建筑工程学院，广州 510632； 2.暨南大学 重大工程灾害与控制教育部重点实验室，广州 510632)

结构损伤检测对结构安全和服役有着重要的意义，近年来引起众多学者的广泛关注和研究[1-5]。一些学者通过分析模态参数对结构参数改变的敏感度建立基于灵敏度分析的结构损伤识别方法[6-7]。由于损伤往往发生在结构局部，因此，将l1范数正则化方法运用到灵敏度分析能产生稀疏解，提高识别精度，改善问题的不适定性。但是，计算得到的灵敏度矩阵各列数值范围相差较大，会致使稀疏求解过程计算效率和识别精度降低；同时，测量噪声等因素影响导致识别结果出现损伤折减系数大于1或者小于0等不合理的情况。

本文通过增加范数归一化与稀疏正则化约束，提出了一种结构损伤检测方法。该方法在灵敏度矩阵修正的过程中，每次迭代均对灵敏度矩阵进行范数归一化，并分别对稀疏求解过程、损伤折减系数改变量以及总损伤折减系数增加约束。稀疏求解过程的约束能限制迭代的方向，使得求解过程指向更加明确；牛顿迭代法约束通过减少步长来提高识别精度；总刚度折减系数约束能改善结果的不合理性。最后，通过三种不同结构数值仿真算例验证了所提方法的有效性。悬臂梁结果表明范数归一化能有效减少迭代成本，增加模型约束能明显提高方法鲁棒性；两层刚架和二维桁架数值仿真进一步验证了新方法的适用性和鲁棒性。

1 结构损伤识别

1.1 灵敏度分析法

由于在实际工程中，结构发生损伤往往可以忽略质量变化，仅考虑刚度变化，因此，本文通过对弹性模量E的折减来描述结构单元的损伤过程。由有限元理论可得，结构的整体刚度矩阵可假设为

(1)

式中：Ki,αi分别为结构第i个单元的单元刚度矩阵和损伤折减系数；N为结构的单元数。

由此可得结构第r阶特征值和第r阶振型关于损伤折减系数的一阶灵敏度计算公式分别为

(2)

(3)

式中：λr,φr(r= 1, 2, …,n)分别为结构的第r阶特征值和第r阶振型；n为结构的总自由度数，则一阶灵敏度识别公式为

(4)

式中：Δfλ= {Δλ1, Δλ2, …, Δλm}T和Δfφ= {Δφ1, Δφ2, …, Δφl}T分别为结构损伤前后的特征值之差和振型差；m和l分别为计算时所采用的特征值阶数和模态振型阶数；Δα= {Δα1, Δα2, …, ΔαN}T为损伤折减系数改变量所构成的向量；S为结构的一阶灵敏度矩阵。

由于SΔα和Δf是近似相等的关系，因此，需要对灵敏度矩阵进行迭代修正，即采用牛顿迭代法进行求解得到更精确的Δα。

1.2 稀疏正则化

由Tibshirani[8]提出的LASSO正则化方法(Least Absolute Shrinkage and Selection Operator，LASSO)，下文简称l1正则化方法，通过对回归系数向量进行l1范数罚来压缩回归系数，并使绝对值较小的回归系数被置零，从而实现回归系数向量的稀疏化。对式(4)添加l1范数罚

min‖Δα‖1subject to‖SΔα-Δf‖2≤ε

(5)

式中：ε为识别结果与理论结果之间的允许误差，其与测量噪声有关。

式(5)可等价于以下的l1范数正则化问题

(6)

式中：β> 0为正则化参数；N为稀疏向量Δα的维数。

本文采用基于近似梯度方法及其变种形式的稀疏优化问题求解软件包SLEP(Sparse Learning with Efficient Progections)[9]对式(6)进行求解，并采用最小信息准则[10](Akaike Information Criterion，AIC)选取最优正则化参数。

2 方法优化

2.1 范数归一化

模态参数对各单元损伤的灵敏度不同，导致灵敏度矩阵各列的数值范围可能存在较大差距。当用近似梯度方法进行迭代求解时，会导致梯度方向偏离最优解方向，使识别精度和速度受到影响。据此，本文对灵敏度矩阵各列进行范数归一化处理，令每个迭代步的梯度方向基本指向最优。归一化具体过程如下：假设把单元1～单元N的损伤折减系数改变量逐次设为1，可以得到此过程的损伤折减系数改变量矩阵为

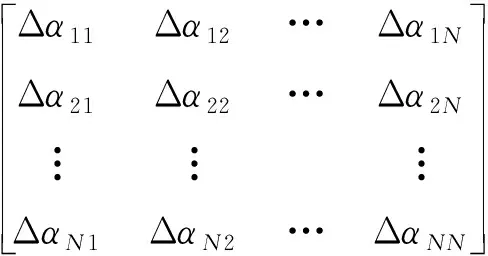
(7)

式中：Δαnorm为N×N的单位矩阵; Δαi(i= 1, 2, …,N)为结构第i个单元发生完全损伤，其他单元无损时对应的损伤折减系数改变量。

把Δαnorm各列分别代入式(4)可得

SΔαnorm=[Δf1, Δf2, …, ΔfN]

(8)

式中：Δfi(i= 1, 2, …,N)对应于Δαi的结构模态变化量。

可以选取任意p(p≥ 1)范数进行范数归一化，本文选取2-范数进行范数归一化，定义范数归一化向量为

P={‖Δf1‖2, ‖Δf2‖2, …， ‖ΔfN‖2}T

(9)

式中：║·║2为向量的2-范数。

对一阶灵敏度矩阵S进行范数归一化

(10)

式中:Si(i= 1, 2, …,N)为一阶灵敏度矩阵S中第i列的所有元素；Se为范数归一化后的一阶灵敏度矩阵。ΔR和Δα之间的关系为

(11)

式中：ΔRi(i= 1, 2, …,N)为ΔR中第i个元素。

2.2 模型约束

2.2.1 稀疏正则化约束

上述方法对噪声比较敏感，鲁棒性较差。近似梯度法在噪声的影响下，其搜索方向波动较大，容易出现误判。本文创新性地对近似梯度法的每次迭代初值进行约束，使其只在约束区域内取值，保证了迭代方向的正确性，达到提高识别精度、减少误判的目的。

稀疏正则化的迭代约束为

(12)

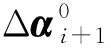
在软件包SLEP求解Δαi的过程中，通过在每次迭代求解前设置初值约束，可达到约束迭代方向的目的。

2.2.2 牛顿迭代法约束

损伤结构的模态参数改变量与损伤折减系数改变量之间是非线性关系，采用灵敏度矩阵修正的灵敏度分析方法实际是利用牛顿迭代法把非线性关系近似为线性关系来寻求问题的解。计算过程中，牛顿迭代法的步长可能比实际损伤折减系数改变量大。加上噪声的影响，由l1正则化方法求得的步长是不合理的，因此需要对牛顿迭代法的步长增加约束

-k≤Δαj≤k

(13)

式中:Δαj为牛顿迭代法第j次迭代的步长；k为牛顿迭代法每次迭代过程的步长范围值，k越小则步长越小，但需要花费更多的迭代时间。

2.2.3 总损伤折减系数约束

由于噪声对实测模态参数的影响，在灵敏度分析过程中，损伤折减系数有可能出现负值，这代表着结构损伤状态的刚度大于无损状态，是不合理的。因此，需要对每次迭代求得的总损伤折减系数增加约束

s≤γi≤1

(14)

式中：γi= 1-αi为某次迭代求得的第i个单元的总损伤折减系数；s=1-t为总损伤折减系数的最小值。

以上结构损伤检测新方法流程图如图1所示。

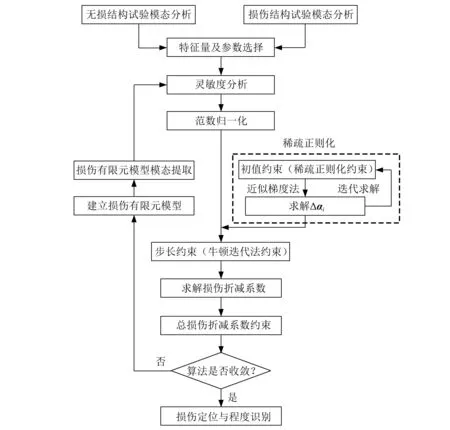
图1 结构损伤检测流程图Fig.1 Flow chart of structural damage detection

3 数值仿真

3.1 范数归一化仿真结果分析

为了验证所加范数归一化的有效性，采用如图2所示的悬臂梁数值算例。悬臂梁长0.7 m、宽0.05 m、高0.01 m，共分为10个单元，圈内数字为单元编号，其余为节点编号。各单元的弹性模量和密度分别是2.01×1011N/m2和7 800 kg/m3。对悬臂梁设置单损伤工况，第2单元损伤5%，取前三阶频率和振型作为输入。在无噪声的情况下考察范数归一化对结构损伤识别结果的影响。识别结果的误差计算公式为

(15)

(16)

图2 悬臂梁有限元模型Fig.2 Finite element model of cantilever beam

识别结果如表1和图3所示。归一化前后灵敏度矩阵各列的范数值如图4所示。从图4可知，灵敏度矩阵各列的范数值随着灵敏度矩阵修正过程而增大；虽然从图3可知，在无噪声的情况下，无范数归一化和有范数归一化的识别结果大致相同，但从表1可知，范数归一化处理后能明显减少迭代时间，提高识别精度。

表1 范数归一化前后悬臂梁的损伤识别结果比较

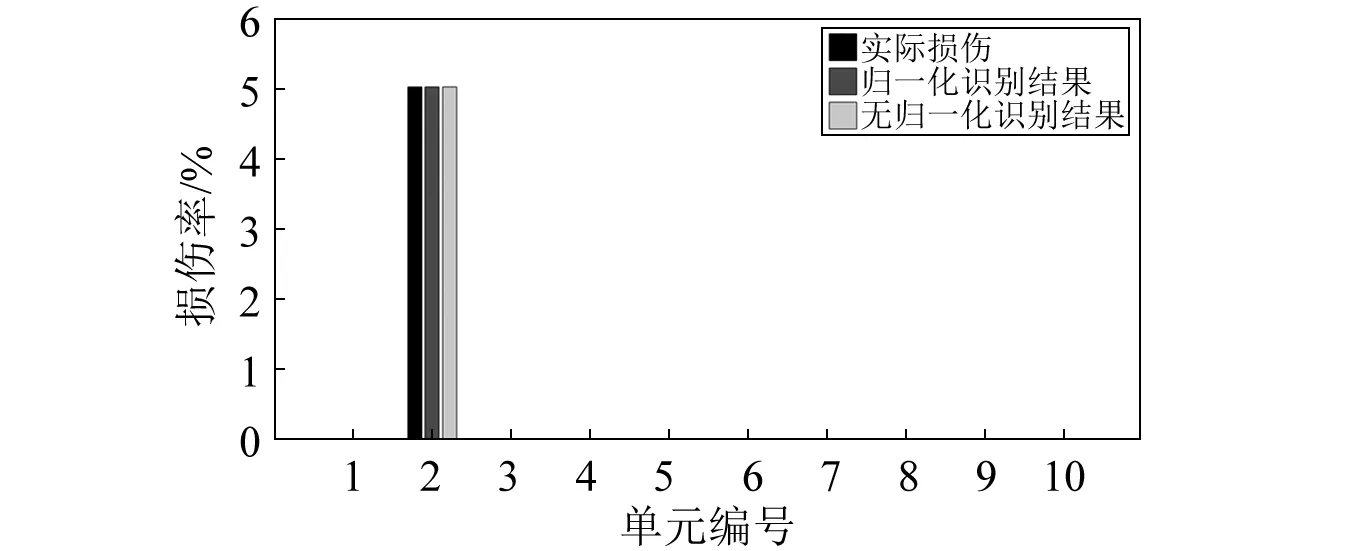
图3 悬臂梁的损伤识别结果(无归一化与归一化)Fig.3 Identified damage results of cantilever beam (non-normalization and normalization)

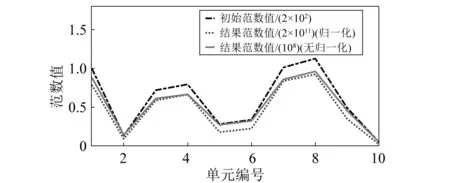
图4 悬臂梁的范数归一化向量结果图(无归一化与归一化)Fig.4 Final norm normalized vector diagram of cantilever beam (non-normalization and normalization)

3.2 约束仿真结果分析

为了进一步验证模型约束的有效性，在范数归一化的基础上，对悬臂梁设置单损伤工况，第5单元损伤60%，同样取前三阶频率和振型作为输入，在15%的噪声水平下考察不同约束对识别结果的影响。

为了便于讨论，本文在以下数值算例均考虑t=k=1-s的情况，且认为损伤率达到90%时，结构失效。

本文考虑噪声的能量与频率和振型改变的能量有关，将参与计算的频率和振型按如下方式添加噪声

(17)

(18)

所设置工况如表2所示。由于实际损伤程度未知，因此无法确定t的合适取值范围，为方便起见，取t=0.9，即结构失效。其中工况2～工况4是只加稀疏正则化约束进行损伤识别；工况5是加稀疏正则化约束和牛顿迭代法约束进行损伤识别；工况6是同时添加三种约束进行损伤识别。

由图5、图6和表2、表3所示的识别结果可以看出，在无约束情况下，损伤识别结果严重失真，出现个别单元刚度强化(数值增长)和损伤单元刚度为负等不合理情况。比较工况2～工况4可知：当t过大，约束不够强，损伤单元的识别精度并没有很大的改善；当t过小，约束太强，近似梯度法在被限制的范围内搜索不到最合适的解。比较工况3和工况5可以看出，在t和k的约束下，受损单元误差和总误差都降低了。在双约束的基础上，增加总损伤折减系数约束，避免了αi<0的不合理情况，且有效地减少了误判。

表2 不同约束下悬臂梁的损伤识别结果比较

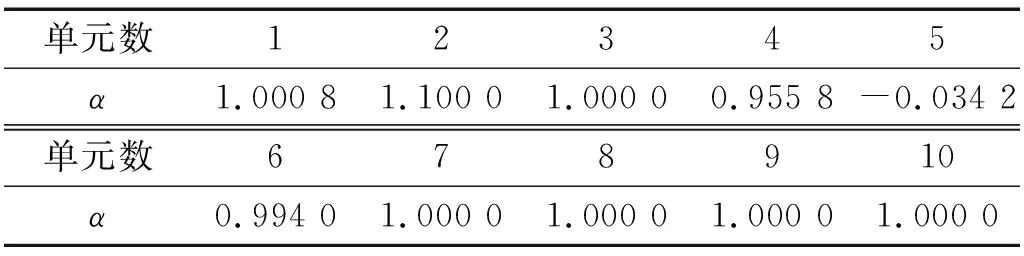
表3 悬臂梁工况1第一次迭代所得损伤折减系数

图5 无约束下悬臂梁的损伤识别结果Fig.5 Identified damage results of cantilever beam under unconstraint condition

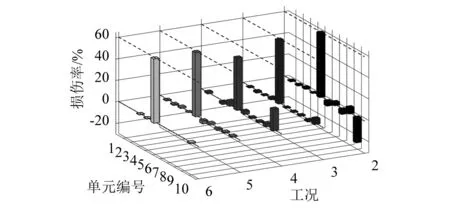
图6 增加约束后悬臂梁的损伤识别结果Fig.6 Identified damage results of cantilever beam via adding constraint

3.3 方法适用性数值分析

t,k和s的取值影响到损伤识别结果，为了确定t,k和s的取值，先在t=k=1-s=0.9的约束下得到损伤识别结果，再由识别得到的单元最大损伤率δ得到t,k和s的取值：t=k=1-s≈δ+0.05。

3.3.1 悬臂梁模型损伤识别

如表4所示设置损伤工况，取悬臂梁前六阶频率和振型作为输入，在不同的噪声水平下考察噪声对识别结果的影响。识别结果如表4和图7所示。从中可知，噪声对损伤识别结果影响不大，没有误判且能精确识别出结构的损伤程度，表明优化后的算法对悬臂梁进行损伤识别有较强的抗噪性。

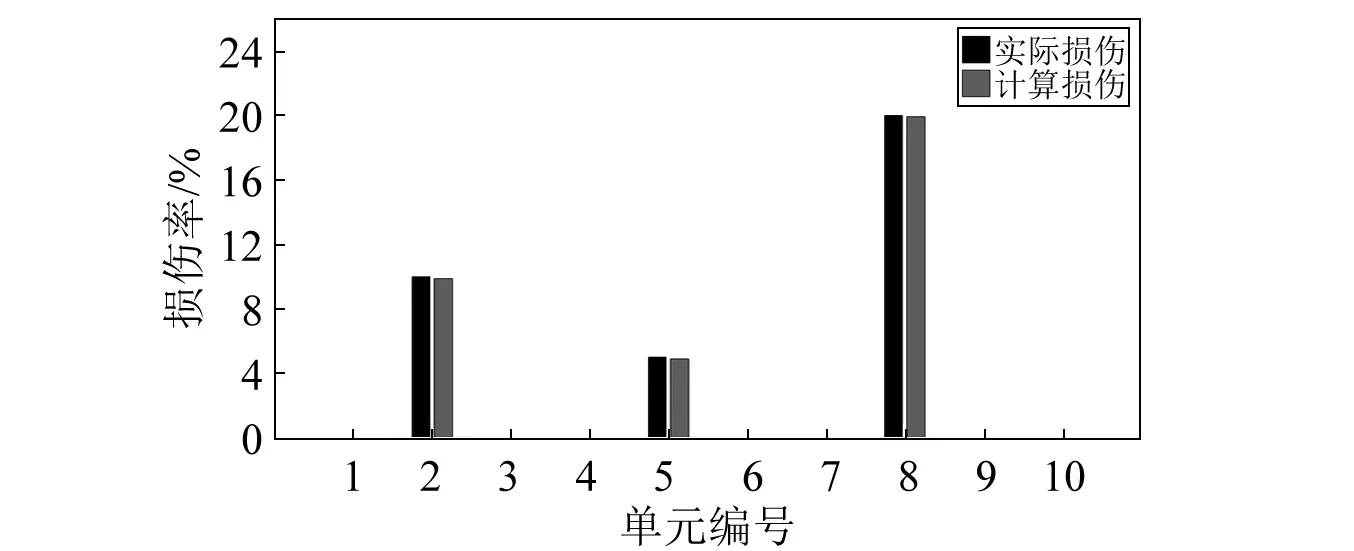
图7 悬臂梁工况3的损伤识别结果(10%的噪声水平)Fig.7 Identified damage results of cantilever beam under case 3 with noise 10%

工况损伤程度/%t , k取值噪声水平5%10%15%15单元损伤100.1510.04110.07810.1025单元损伤100.259.9619.9229.8848单元损伤2019.96619.93119.90035单元损伤50.254.9434.8914.8428单元损伤2019.96219.92119.8882单元损伤109.9489.9069.858

3.3.2 刚架模型损伤识别

进一步考察本文提出方法在图8所示二层刚架模型[11]的适用性。

每层刚架的高和宽均为1.41 m。共分为18个单元，框内数字为单元编号，其余数字为节点编号，刚架其它参数见表5。取前六阶频率和振型作为输入，如表6对刚架设置损伤工况，在不同的噪声水平下考察噪声对识别结果的影响。从图9和表6识别可知，在噪声的影响下，识别精度随着噪声水平的增大而下降，局部单元有损伤率较小的误判出现，计算损伤与实际损伤存在上下波动，但仍能较为准确地识别损伤。

表5 刚架参数

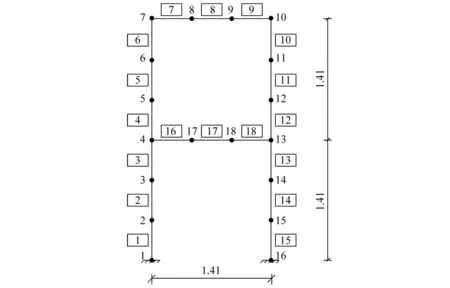
图8 刚架有限元模型Fig.8 Finite element model of rigid frame

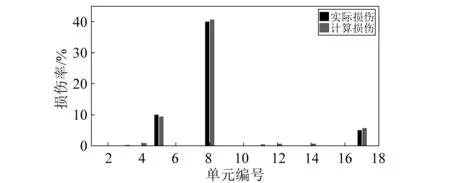
图9 刚架工况3的损伤识别结果(10%的噪声水平)Fig.9 Identified damage results of rigid frame under case 3 with noise 10%

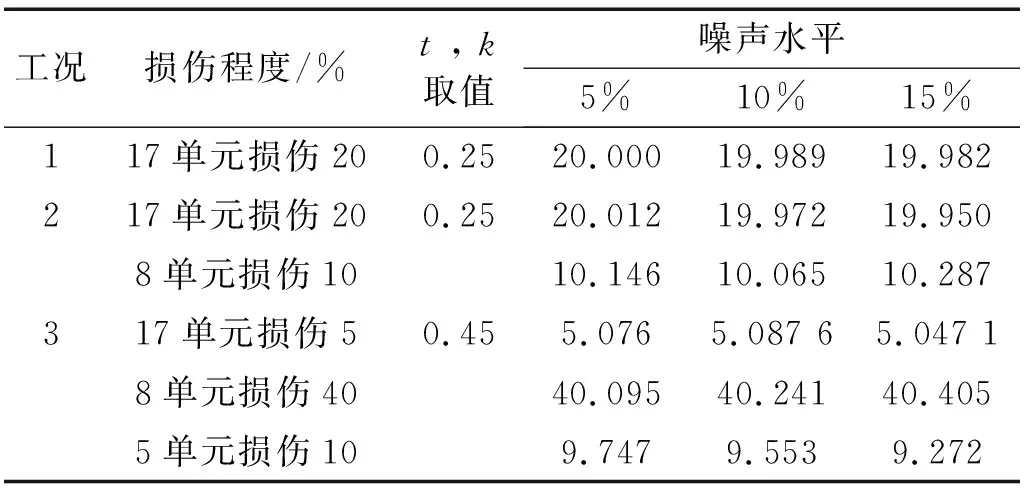
工况损伤程度/%t , k取值噪声水平5%10%15%117单元损伤200.2520.00019.98919.982217单元损伤200.2520.01219.97219.9508单元损伤1010.14610.06510.287317单元损伤50.455.0765.087 65.047 18单元损伤4040.09540.24140.4055单元损伤109.7479.5539.272

3.3.3 桁架模型仿真

同样，进一步以图10所示二维桁架验证所提损伤识别方法的适用性。

桁架总长为5 m，高0.5 m。共分为40个单元，其中圈内数字为单元编号，其余为节点编号。材料的弹性模量、密度和横截面积分别是2.1×1011N/m2，7 800 kg/m3和0.003 m2。取前六阶频率和振型作为输入，在不同的噪声水平下考察噪声的影响，如表7设置桁架的损伤工况。识别结果如表7和图11所示。由表7和图11可以看出虽然损伤识别结果出现少量误判，但损伤识别结果精度较高，基本不受噪声的影响。

表7 桁架损伤工况及损伤单元识别结果(损伤率%)

图10 二维桁架有限元模型Fig.10 Finite element model of truss

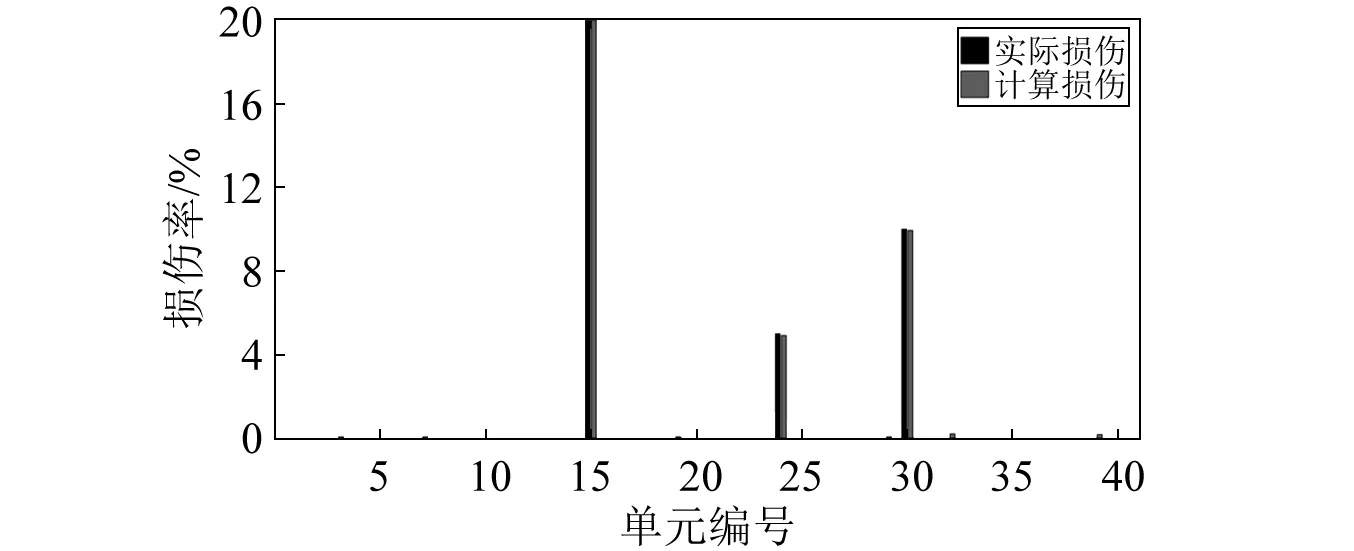
图11 桁架工况3的损伤识别结果(10%的噪声水平)Fig.11 Identified damage results of truss under case 3 with noise 10%

3.3.4 仿真结果分析

由上述三个仿真算例的损伤识别结果可知：① 在各种噪声水平下，所提方法均能有效定位损伤并精确识别损伤程度；②噪声对损伤识别结果影响不明显，表明所提方法具有较强鲁棒性；③三种模型中，悬臂梁的损伤识别结果最好，刚架和桁架均存在小于1.5%的误判，虽然单元损伤程度大小与实际损伤存在上下波动，但仍能较好地定位损伤和识别损伤程度。因此，所提方法在三种模型的数值仿真算例中均能有效且准确地识别损伤位置和损伤程度。

4 结 论

本文通过约束结构损伤识别稀疏解，提出了一种基于范数归一化与稀疏正则化约束的结构损伤检测方法。该方法通过对灵敏度矩阵修正迭代过程进行范数归一化处理，并分别对稀疏解、损伤折减系数改变量以及总损伤折减系数增加约束，达到提高损伤识别效率和精度的目的。三种不同结构模型数值仿真算例验证了所提方法的有效性、适用性和鲁棒性。结论如下：

(1) 范数归一化能把灵敏度矩阵各列的数值范围控制在相同量级内，提高了方法的收敛速度和识别精度。

(2) 稀疏正则化约束参数t取值合理时，可以得到较准确的结构损伤识别结果；当不能确定稀疏正则化约束参数t的取值范围时，可通过控制牛顿迭代法的步长k，对方法加强约束，获得准确的损伤识别结果；增加总损伤折减系数约束s不仅能提高结果的合理性，而且能减少单元误判，提高识别结果精度。

(3) 三种不同结构的数值仿真研究表明：本文所提方法既能有效定位结构损伤又能准确识别损伤程度，且对噪声不敏感，具有较强鲁棒性。