基于PSO-LSSVM的锂离子电池荷电状态预测方法*

黄永红，沈洋洋，陈坤华，周杰，李冬

(1.江苏大学 电气信息工程学院, 江苏 镇江 212013； 2.国网苏州供电公司, 江苏 苏州 215004)

0 引 言

锂离子电池由于容量大、能量密度高、无记忆性的优点，被广泛应用在电动工具、电动自行车、电动摩托车、电动汽车、军事装备、航空航天等多个领域。为了稳定的发挥电池性能，提高电池使用寿命以及工作安全性，避免电池过度充电和深度放电，准确的估测电池[1]的荷电状态(SOC)具有非常重要的意义。为了实现SOC准确在线预测，文献[11]提出了一种机载蓄电池SOC估计方法，该方法基于放电试验法对其荷电状态进行估计。文献[12]结合传统安时积分法、开路电压法及负载电压法，综合考虑充放电效率、温度等因素的补偿措施，提出一种新型SOC安时积分实时估算方法。文献[13]通过电池恒流充放电特性实验，得到锰酸铁锂电池开路电压与对应SOC的关系曲线及电池放电自恢复曲线。以上方法虽可以预测电池SOC，但都是根据电池的内在物理属性去预测，建立相应的电池模型时包含一定的假设和经验成分，难以达到精确的估算。此外，还有些SOC预测方法如：卡尔曼滤波器[3-4]便于计算机编程,并能够对现场采集的数据进行实时的更新和处理，但计算量大，周期长，对硬件性能要求高。神经网络法[5-6]非线性拟合能力强，但大量的样本数据和综合训练在很大程度上会影响到SOC预测的准确度。

为此，提出一种PSO-LSSVM算法来实时预测锂离子电池的SOC。其优点是在一定的样本数据下，使得锂离子电池SOC估算误差较小，并且不用考虑电池的内部物理特性。因此，可以保证预测精度。利用 LSSVM 建立软测量模型时，两个主要因素直接影响着模型的准确度，一是正则化参数λ，二是径向基核宽度μ，故二者参数的优化选择十分重要。采用粒子群优化算法(PSO)对这两个参数进行优选[7-8]，该算法易于快速找出全局最优解，具有方法简单、效率高、易实现等优点。以蓄电池工作电压、电流为输入量，电池SOC为输出量建立软测量模型[2]，通过MATLAB仿真软件进行模型训练并校正，试验验证了PSO-LSSVM 的精确性。

1 最小二乘支持向量机模型建立

支持向量机[10]是根据结构风险最小化原则和统计学习理论所提出的。在训练样本的过程中，SVM存在求解二次型优化问题。LSSVM通过把不等式约束条件变成等式约束条件，将标准SVM 采用最小二乘线性系统误差平方和作为损失函数情况下的一种特殊形式。

1.1 LSSVM原理

在一定数量的样本集合下{ai,bi},i=1,2,……,N，样本集合的空间维数为n，ai为样本输入向量，bi为样本输出向量。在LSSVM算法中引入非线性映射函数η(*)，空间样本被映射到函数η(ai)中，从而将低维空间的非线性函数逼近问题变为线性函数的逼近问题。在高维空间中LSSVM模型可以表示为：

y(a)=θTη(a)+c

(1)

式中θ为权矢量;c为偏差量。

为得到风险最小化，需要寻找适当的θ、c：

(2)

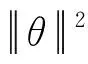
故该优化为：

(3)

约束条件为：

yi=θTη(ai)+c+βi

(4)

式中βi代表松弛因子。

为了快速地找到该函数的最小值，运用拉朗日法对该问题优化求解：

(5)

式中di代表拉格朗日因子。

根据KKT条件对式(5)进行处理，微分得出：

(6)

(7)

(8)

(9)

1.2 SOC预测模型核函数的选择

根据MERCER条件，定义核函数为：

η(ai,bj)=ηT(ai)η(bj)

(10)

故将优化问题转化为下面的线性方程组：

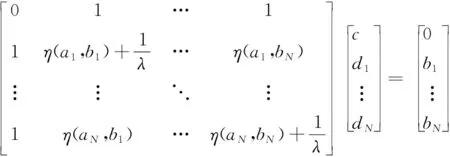
(11)

通过利用最小二乘法对该算法进行优化求解，得出c、d的值，推断出最小二乘支持向量机模型如下：

(12)

文中选取的基核的函数为：

(13)

式中μ表示基核宽度。

由上述分析可知，该预测模型的精确度受到λ和μ的影响。为了避免由于经验、随机选择造成的误差，故使用PSO对该参数进行优化。

2 基于粒子群优化的最小二乘支持向量机

2.1 粒子群优化算法原理

粒子群算法是从随机解角度考虑，最优解是通过迭代寻找最优解，其中适应度用来衡量最优解的质量，其规则简易，通过追随当前搜索到的最优值来寻找全局最优。每个粒子代表着一个解，该解空间包含位置矢量和速度矢量。对任意一点粒子i来说，位置向量ei=(ei1,ei2,……ein)，速度向量vi=(vi1,vi2,……vin)。单个粒子经历过的最优解的向量标记为li=(li1,li2,……lin)。种群所有粒子经历的最优解向量标记为lq=(lq1,lq2,……lqn)。在该算法中通过以下公式进行迭代：

viu(h+1)=ωviu(h)+k1p1(liu(h)-eiu(h))+k2p2(lqu(h)-eiu(h))

(14)

eiu(h+1)=eiu(h)+viu(h+1)

(15)

其中ω为权重系数，u=1,2,……,n，n为空间维数；h为迭代次数，i=1,2,……,s，s为种群样本个数，p1,p2为随机数在0和1间。k1,k2是正常数。为了降低随机性，学习因子c1=c2=2；viu∈[-vmax,vmax]，vmax是粒子最大飞行速度，同时该数值决定了搜索的精度。若数值过大，则直接飞越最优解；若数值过小，则只能进行局部寻优。eiu∈[-emin,emax]，eiu由实际的情况决定。粒子速度的取值通常取决于该粒子位置，一般情况下该数值为vmax=kemax。

2.2 粒子群权重参数的选择

粒子群算法中，为了平衡局部和全局搜索，要适当的进行参数ω的选择。当ω大时，全局大于局部搜索能力，当ω小时，全局小于局部搜索能力。故在粒子群算法中，前期获得全局收敛，后期不会陷入局部寻优。权重参数ω应该随着h的变化从ωmax逐渐变为ωmin，他们应该满足的关系式为：

(16)

式中H为最大迭代次数。

3 SOC预测模型参数优化

结合PSO算法，对LSSVM正则化参数λ和径向基核宽度μ的选择进行优化，流程图如图1所示。

参数优化具体步骤如下：

(1)对粒子群体各个参数进行初始化，包括c1、c2、H、ωmin、ωmax、ei、vi等。

(2)计算每个粒子的适应度。适应度公式为：

(17)

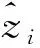
(3)通过计算适应度和最优适应度相比较，更新适应度，同时保存相应的参数值。

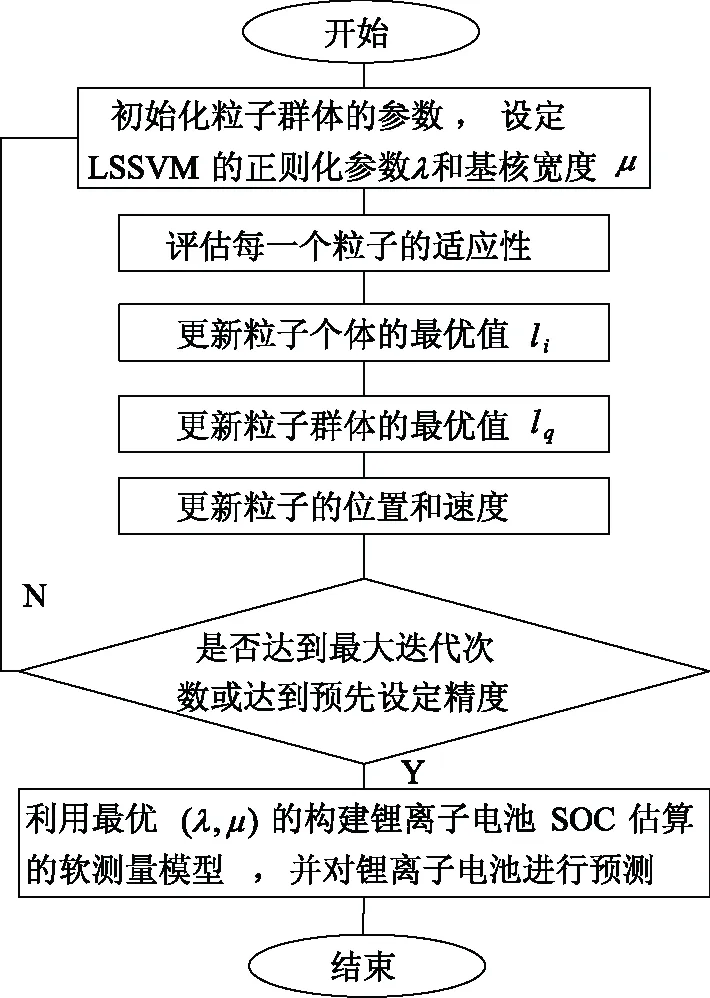
图1 LSSVM参数优化流程

4 实验及仿真

4.1 样本数据采集

采用10组单体电压为3.6 V锂离子电池相串联，组成电压、容量为36 V、10 Ah的电池组作为研究对象，利用型号为BTS6050C4的NBT电池测试系统，在常温条件下，充放电过程中每20 s采集一组电压、电流以及容量，14 000 s内总共收集到700组采样数据。实验获取一个充放电循环五个工步数据，工步类型依次为：静置—恒流充电—恒压充电—静置—恒流放电—静置。起始数据如表1所示。

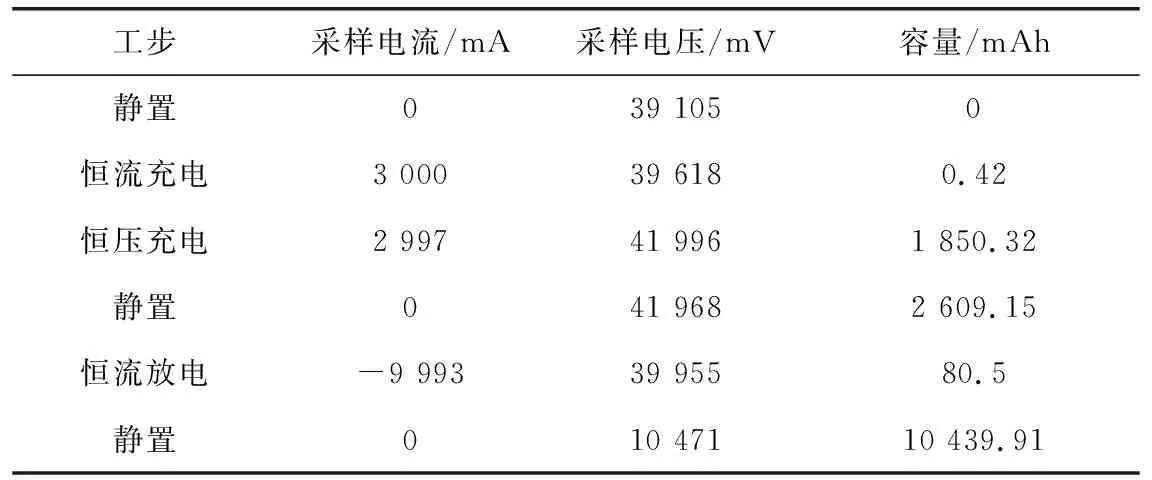
表1 电池测试系统下各工步起始数据

在NBT电池测试系统下，获得一个周期的充放电电压、充放电电流及电池容量的真实值随时间变化的数据曲线如图2～图4所示。

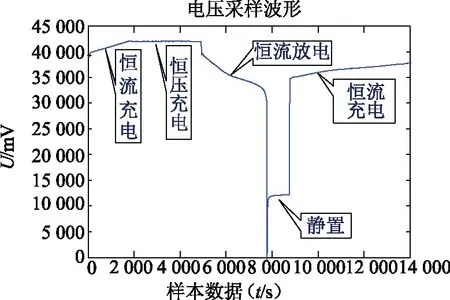
图2 锂离子电池充放电电压曲线

图3 锂离子电池充放电电流曲线

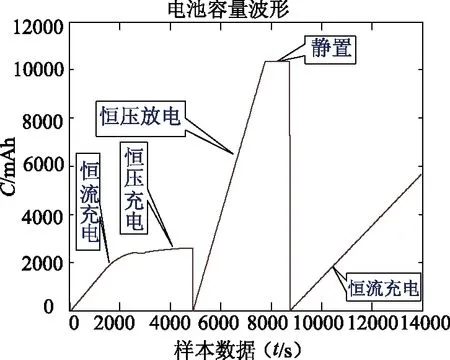
图4 锂离子电池电池容量变化曲线

图2、图3中为该测试系统一个充放电循环五个工步下蓄电池充放电曲线，图中看出在0 s～2 000 s时，蓄电池采用恒流充电，在时间2 000 s～5 000 s时，蓄电池采用恒压充电，在5 000 s～8 000 s时，蓄电池采用恒流放电。在8 000 s～9 000 s时，蓄电池处于静置状态。在9 000 s～14 000 s，蓄电池处于恒流充电状态。图4是在0 s～14 000 s蓄电池电池容量随着时间变化的曲线，其中在8 000 s～9 000 s时，蓄电池出现了略微的过充。

4.2 仿真及分析

为了验证PSO-LSSVM的优越性，通过利用Matlab/Simulink仿真软件进行仿真，以蓄电池工作电压、电流为输入量，电池SOC为输出量建立预测模型。利用文中所述的 PSO-LSSVM 算法步骤进行模型参数优化，得到最优化的正则化参数λ=372 526.068 47，径向基核宽度μ=81.644 13，权重系数ωmax=0.9，ωmin=0.3，最大迭代次数H=200，学习因子c1=c2=2。通过这些参数以及软件仿真得出预测结果并与SVM、LSSVM两种算法得出预测值进行了对比分析，如图5、图6所示。

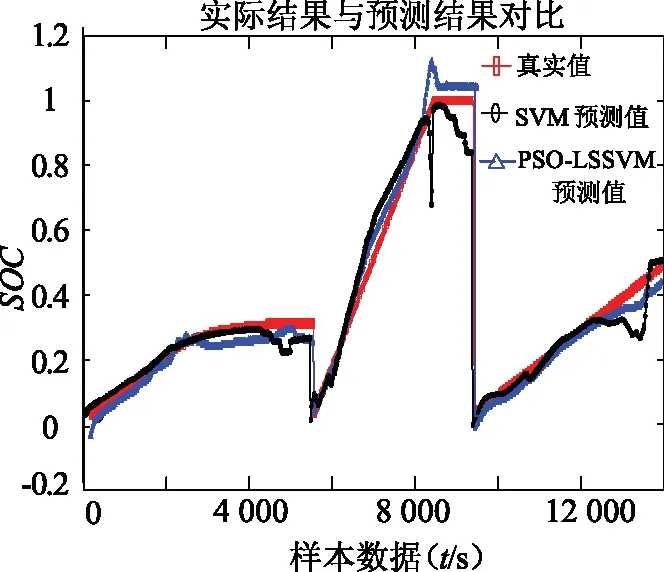
图5 SVM与PSO-LSSVM预测结果

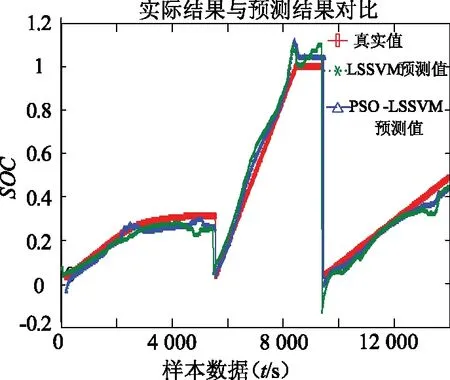
图6 LSSVM与PSO-LSSVM预测结果

从图5、图6分别可以看出，相比于SVM和LSSVM，在0 s～8 000 s之间PSO-LSSVM预测数据更接近真实值。在8 000 s～9 000 s之间，电池出现过充，PSO-LSSVM的预测精度和稳定性优于SVM和LSSVM。在9 000 s～14 000 s时，SVM和LSSVM波动较大，PSO-LSSVM稳定性高。

为了直观分析PSO-LSSVM模型预测的精确性，给出了PSO-LSSVM预测值和LSSVM、SVM 预测值的绝对误差曲线，如图7、图8所示。

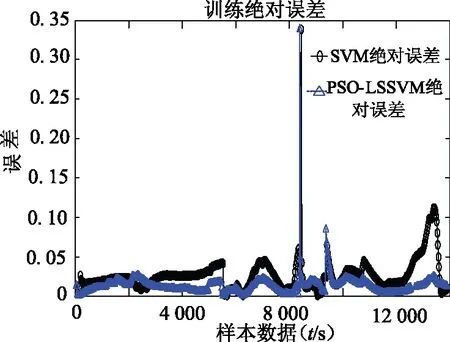
图7 SVM与PSO-LSSVM绝对误差曲线

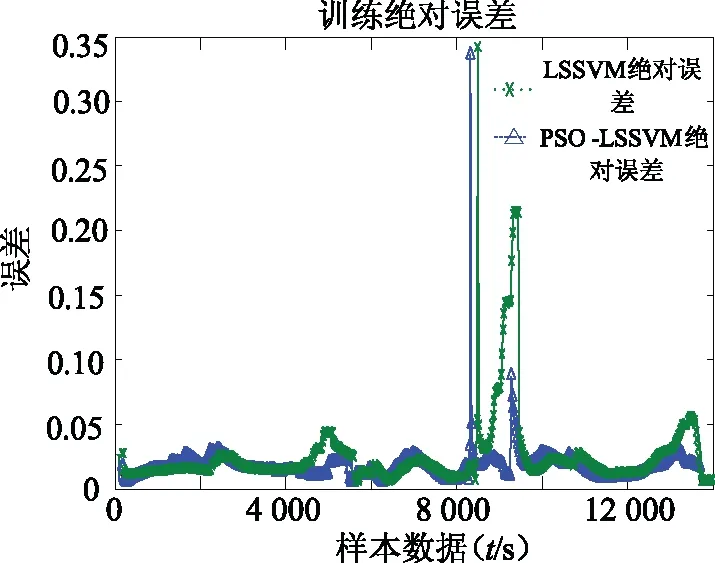
图8 LSSVM与PSO-LSSVM绝对误差曲线

图7、图8中，在0 s～8 000 s和9 000 s～14 000 s时，PSO-LSSVM的绝对误差最低，介于0～0.05之间。在8 000 s～9 000 s，电池发生过充电时，模型的预测偏差变大，但PSO-LSSVM预测值偏离真实值程度最小，由此可见该模型预测的精确性高。SVM预测值的相对误差曲线如图9、图10所示。

由图9、图10的相对误差曲线可看出，在0～8 000 s和9 000 s～14 000 s时，PSO-LSSVM相对误差大多数介于0.05～0.12之间。在8 000 s～9 000 s时，当电池

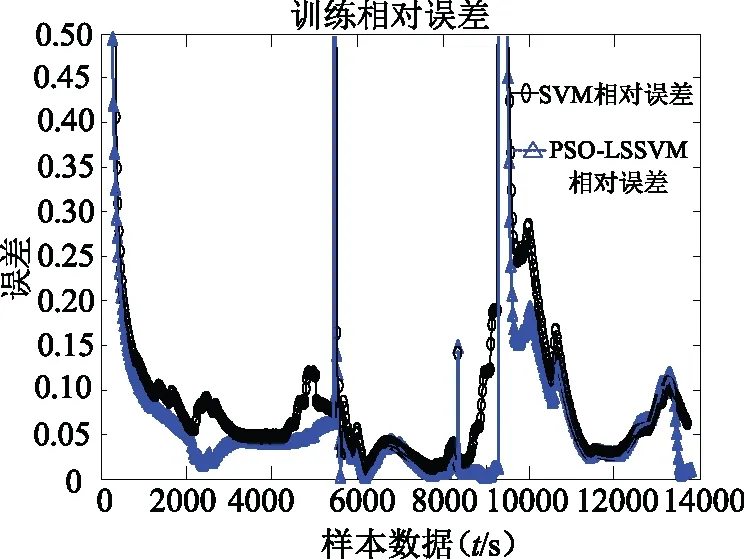
图9 SVM与PSO-LSSVM相对误差曲线

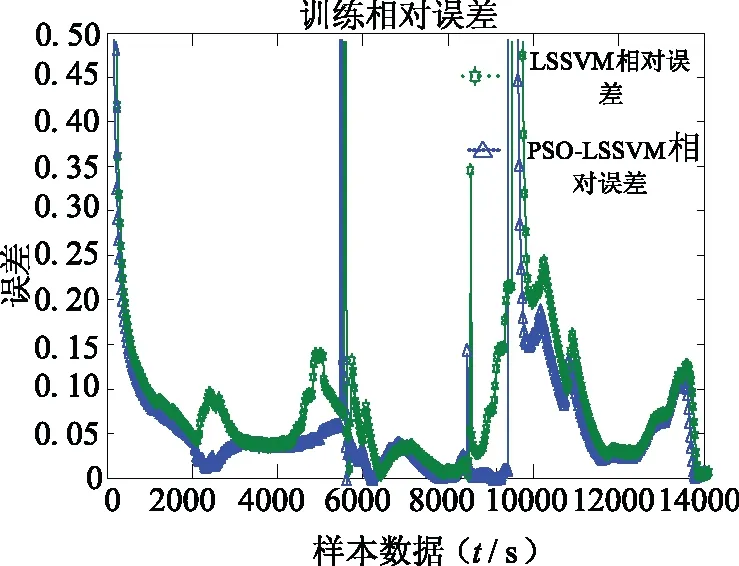
图10 LSSVM与PSO-LSSVM相对误差曲线

发生过充电时，所有模型的相对误差偏大，但PSO-LSSVM整体相对误差最小，进一步说明了PSO-LSSVM预测模型的精确度高。

表2是模型的部分性能比较。均方误差反应模型的整体性能，数值越低表明整体性能越好。决定系数范围在[0,1]内，愈接近于1，表明模型的性能愈好。预测时间长短则表明模型的计算复杂度高低。

表2 模型的部分性能比较

从表2看出，PSO-LSSVM均方误差最低，决定系数最高，预测时间最短，表明PSO-LSSVM模型的预测精度高，计算复杂度低。

5 结束语

(1)粒子群优化最小二乘支持向量机软测量算法(PSO-LSSVM)可用于锂离子电池SOC预测，不用考虑锂离子电池的内部物理属性；

(2)采用粒子群算法(PSO)对LSSVM两个关键参数正则化参数λ和径向基核宽度μ进行优化，可以提高预测模型的稳定性，减少迭代次数和运行时间；

(3)仿真和实验结果表明PSO-LSSVM模型在线预测比LSSVM和SVM模型预测精确度高、稳定性强、易实现，且在正常和过充工作状态下均可有效的进行蓄电池SOC在线预测。