基于系数估值约束的改进LMS自适应滤波算法

王艳

(1.西安欧亚学院 金融学院， 西安 710061； 2.西安交通大学 软件学院, 西安 710061)

0 引 言

无线传感器技术的快速发展，使得新的网络结构和算法被不断提出，分布式网络估计通过节点间的信息共享增强了计算的鲁棒性和估计的准确性，在精确农业、环境监测等实际工程中广泛应用[1]，分布式估计的性能，直接影响着能否对未知系统更加准确快速的进行估计，而将自适应滤波与无线传感器网络有效结合，成为分布式估计的研究热点[2]。为此，Lopes等人[3]将扩散算法与LMS算法结合，提出了扩散LMS算法，受到广泛关注，但其基于节点能量和数据通信是无限制的。Cattivelli等人[4]提出基于扩散式的DLMS算法，能够有效地实现分布式估计，但在实际工程中常遇到脉冲噪声干扰，估计性能降低；Wen等人[5]提出DLMS/F算法进行改进，尽管有效处理了脉冲干扰，但是稳定性脆弱；Ni等人[6]通过对误差函数进行符号函数化提出DSELMS算法，算法结构简单且在处理脉冲噪声时性能非常优越，但其算法稳态误差大；陈文晓等[7]提出了在扩散LMS算法中先后采用符号函数和改进的符号函数量化策略，解决网络中数据运算量大及传输速率受限问题；张勇刚[8]等提出了一种SDVTNLMS算法，解决固定阶数算法不能很好解决阶数未知或时变参数的问题。

综上所述，如何设计分布式自适应滤波算法，使其具备快速收敛和低稳态误差，是目前急需解决的问题。为此设计了一种基于未知参数估计值约束的改进LMS自适应滤波算法，通过相邻迭代的参数估计值约束迭代步长，保证算法的快速收敛和低稳态误差，仿真实验结果验证了算法的有效性。

1 扩散LMS自适应滤波算法

图1所示为空间分布的由K个传感器组成的强连接网络，其中第k个传感器在时刻i测量值为dk(i)，dk(i)∈dk(i)，其相应的1×M维回归向量为Xk(i)，Xk(i)与dk(i)都是零均值的随机过程，则自适应滤波的目标为通过{Xk(i),dk(i)}估计分布式网络中每个节点的参数向量W0∈CM×1，则第k个节点的输出信号测量值为：

(1)

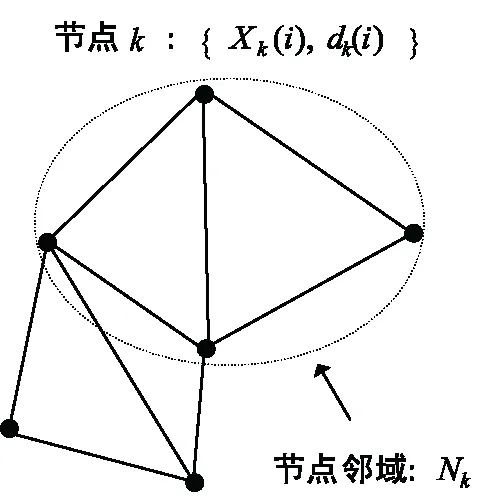
图1 K个传感器组成的分布式网络

则图中节点的参数向量W0∈CM×1可以通过式(2)传统LMS算法所示的全局最优代价函数计算。

(2)

式中E(·)表示计算数据期望。扩散LMS算法[3]将当前时刻节点k的邻居节点参数估计值Wj(i-1)，j∈Nk融入到下一时刻k局部自适应滤滤器中进行W0的估计。其局部迭代方法为：

(3)

ek(i)=dk(i)-Xk(i)Φk(i-1)

(4)

Wk(i)=Φk(i-1)+μkek(i)Xk(i)

(5)

式中 常数μk>0为迭代步长；Nk为节点k的邻居节点集合(包括k节点自身)，如图1所示，其为与节点k有直接通信链路关系的节点的集合，正实数ck,j为各节点的融合权值且满足：

∑j∈Njck,j=1，ck,j=0 ifj∉Nn

(6)

扩散LMS算法简单受到广泛关注，但其基于节点能量和数据通讯是无限制的假设，与实际不一致[9-10]，为此引入未知参数估计值约束，提出基于参数估计值约束的分布式自适应滤波算法。

2 基于参数估值约束的自适应滤波

在扩散LMS自适应滤波基础上，对全局最优代价函数(2)使用式(7)所示的局部最优代价函数:

(7)

式中通过将未知参数估计值约束加入到局部最优代价函数中，通过相邻两次迭代结果差控制迭代步进，以加快迭速率，减少计算量和节点通信量。

根据式(7)算法主要包括参数融合和自适应迭代两部分，节点k的参数估计中间值：

(8)

式中μ0是收敛初始步长;δ是很小的正数，防止分母为0无意义;ek,i=dk(i)-Xk(i)Wk(i);φk是局部中间估计值。计算所有节点的中间值后，则节点局部参数估计值为：

(9)

式中Nk为节点k的邻居节点集合;正实系数ck,j是融合权值，用来确定邻居节点参数对节点k的贡献度，且当j∉Nk时，ck,j=0。

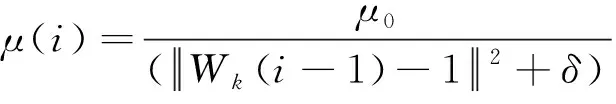
提出的分布式自适应网络滤波算法流程如下：

初始化：对所有节点n的初始化参数都是{wk,-1=0}，δ，μ。

设定非负的融合权重{ck,l}且满足∑l∈Nkck,l=1，对每个节点都进行多次迭代。则第k个节点在第i次的迭代表达式为：

φk(i)=Wk(i-1)+

3 算法收敛性分析

为了便于后面分析，先给出以下定义，系统参数真实值与估计值差值为:

Vk(i-1)=Wo-Wk(i-1)

(10)

Φk(i-1)=Wo-φk(i)

(11)

系统的所有系数估计值为：

W(i) = col {W1(i),W2(i),…,Wk(i)}

(12)

φ(i) = col {φ1(i),φ2(i),…,φk(i)}

(13)

由真实值与估计值差值组成的向量为：

V(i) = col {V1(i),V2(i),…,Vk(i)}

(14)

Φ(i) = col {Φ1(i),Φ2(i),…,Φk(i)}

(15)

则式(8)和(9)化简式为:

Φ(i)=V(i-1)-ΓS(i)X(i)

(16)

V(i)=ATΦ(i)

(17)

式中⊗表示Kronecker乘积;

A={ck,j}，A=A⊗Ik;

S(i)=diag(en(i))，S(i)=S(i)⊗Ik;

X(i) = col {X1(i),X2(i),…,Xk(i)};

Γ(i) =

结合式(16)和(17)可得式(18)。

V(i)=ATV(i-1)-ATΓS(i)X(i)

(18)

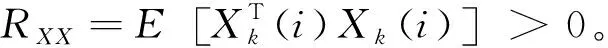
E[V(i)]=ATE[V(i-1)]-ATΓE{S(i)X(i)}

(19)

式(18)等号两端取数学期望后，对于第k个传感器，当取数据期望后的式(19)收敛，则有步长μ(i)的约束区间为：

(20)

即在式(19)所给定的区间内，分析式(18)的数据期望，可得E[Vi(∞)] = 0，表明所提算法能对目标进行有效地估计。

4 实验分析

实验验证文中算法的性能，实验环境为Inter(R) Core(TM) i5-2430M CPU @ 2.40 GHz、6.00 G内存，MATLAB R2016a软件。实验对比算法为：DSELMS[6]、DLMS[4]、DLMS/F[5]和文中算法(记为EILMS。在脉冲干扰下进行系统识别，系统长度L=15，噪声为基于概率p(1)=Pr的Bernoulli序列，由模型v(i)=A(i)·I(i)生成，A(i)表示零均值、方差为0.01的高斯序列。信号采样点数为10 000，蒙特卡洛次数为50。无线传感器网络由20个节点组成。采用均方误差来衡量算法性能:

(21)

4.1 实验设置

如图2所示为实验使用的网络连接图，其中 图2(a)所示为第一组实验网络连接图，当两节点连接且距离L≤0.3时，认为是相互连通邻居节点，Pr=0.1，图2(b)所示为第二组实验使用的网络连接图，当两节点之间的连通概率大于或等于0.2时认为是相互连通的邻居节点，Pr=0.03。

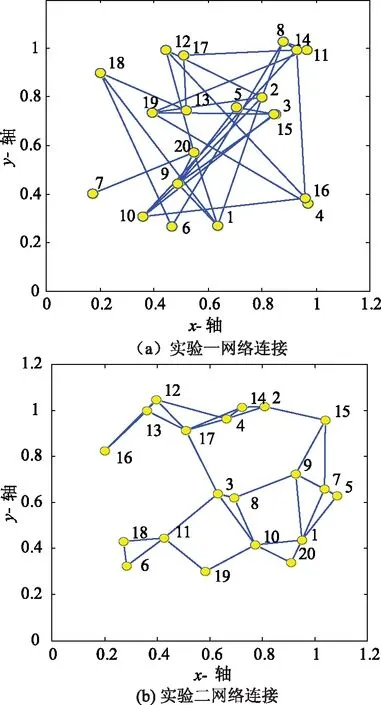
图2 实验采用的分布式网络

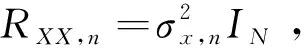
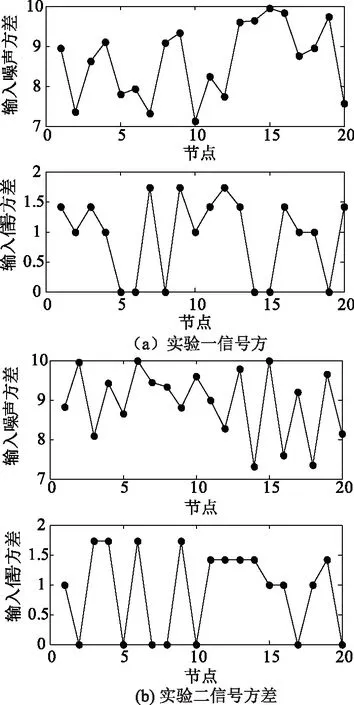
图3 实验使用的信号和噪声的方差

4.2 实验结果分析

图4和图5所示为4种算法参数估计值MSD曲线，相比于DSELMS算法，EILMS算法稳态误差更小；而与DLMS算法和DLMS/F算法相比，EILMS算法的收敛速度有明显优势，从两组实验结果可看出所提算法在收敛速度和稳态误差方面都取得较好的效果，主要因为在算法运行初期Wk(i)较小，算法具有较快的收敛速度，而算法后期μ(i)与μ(i-1)相差不大，保证了算法具有较小的稳态误差。

DSELMS算法由于直接对估计误差en(i)进行非线性约束使其等效步长在收敛初期比较大，能够快速收敛，但是其在稳态误差方面性能表现不够优越。同DSELMS算法原理相似，文中算法运行初期通过较小的预设Wk(i)值，从而使算法具有较快的收敛速度，而当算法趋于稳定时，通过调整抱定代步长，相比于DSELMS算法，又可获得更小的稳态误差。

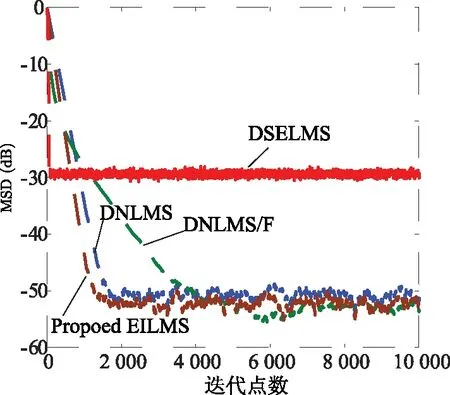
图4 参数估计值随迭代数的MSD曲线

图5 参数估计值随迭代数的MSD曲线

从表1实验结果可知：相比DSELMS、DLMS和DLMS/F算法，EILMS算法在保证收敛速度的同时，在稳态误差方面分别改进了23.4 dB、3.1 dB和0.3 dB；22.9 dB、2.2 dB和1 dB。

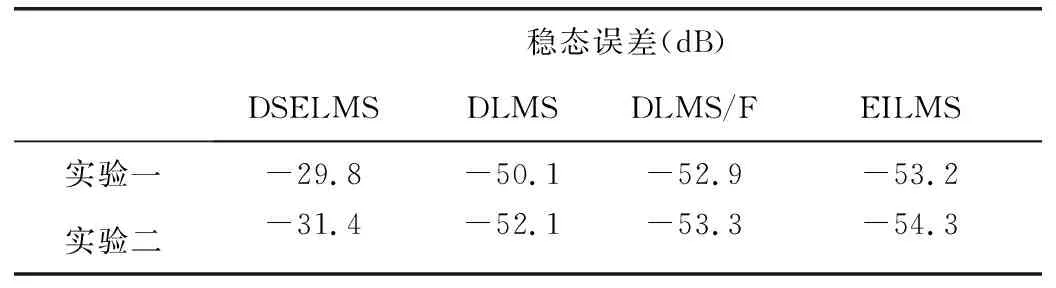
表1 实验中所得稳态误差

5 结束语

在进行分布式估计时，为了同时具备快的收敛速度和低的稳态误差，同时结构简单又能处理受脉冲干扰的系统，提出一种适用于分布式网络的通过系数估计值的范数值调整算法迭代步长的改进自适应滤波算法，分析了其收敛发性能。实验结果表明，相比已有算法，文中算法性能更优。