风电机组输出功率平滑技术综述

朱 瑛， 高云波， 臧海祥, 徐 聪， 郝荣国， 石卫军

(1. 河海大学能源与电气学院， 江苏省南京市 211100; 2. 国电南瑞科技股份有限公司， 江苏省南京市 211106)

0 引言

风能作为21世纪以来受到重视的一种新能源，在全国乃至全世界的装机容量都逐年提高。截至2016年底中国累计风电装机容量为168 690 MW，占全球装机容量的34.7%。尽管风能与其他能源相比拥有清洁、无污染的特点，但随着风力发电规模不断扩大，风电功率波动问题愈发严重，这对电网的频率、电压、动态稳定等方面产生不可忽视的影响[1-3]。

风电输出功率平滑是指由于风能的不确定性导致风电机组向电网出力时发生幅度较大的功率波动，无法满足电网的功率限幅标准，而采用某种手段调整风电机组输出功率的平滑度。目前，主要有三类方法对风电输出功率进行平滑。

第1类方法是加装储能装置的间接功率控制来进行功率平滑，其中包含蓄电池储能、超级电容储能、飞轮储能、超导储能等装置，它们的特点是通过能量的快速充放来频繁地响应输出功率的波动，可操控性较高，无须改变风力机组控制结构。第2类方法是不加储能装置的直接功率控制，通过风电机组自身的调节控制达到功率平滑的效果，其中包含利用转子动能存储、变桨距控制、直流母线电压控制等方法，它们的特点是由于无须附加装置，经济成本较低。还有一类方法是风电场风电机组分层控制平滑策略,该方法将控制方案分为几层，每一层分别执行对应的控制策略，通过不同控制层间的相互协调而达到整体目标最优效果[4-5]。该方法通过调度的原理来控制风电场的输出功率，目前研究较少。

本文从风电机组控制角度出发，对上述最常见的直接功率控制和间接功率控制这两类输出功率平滑方法进行原理分析，然后对各类方法的特点进行归纳总结，比较其优缺点，最后对风电功率平滑方法的研究方向和前景做出展望。

1 基于储能装置的间接功率控制平滑方法

1.1 基于蓄电池储能的功率平滑

蓄电池平滑功率原理是根据功率控制指令，利用电池正负极的化学反应进行充放电，进而起到功率平滑的作用，几种常见类型的蓄电池参数如表1所示[3]。

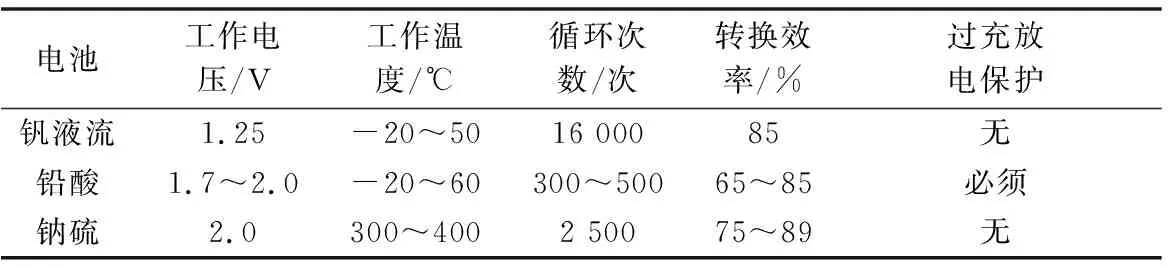
表1 各种蓄电池的性能比较Table 1 Comparison of various battery performances

当前蓄电池储能系统(BESS)在风力发电系统中得到了较多的应用[6-10]，风电场配置的BESS如图1所示，单台风力发电机组配置BESS如图2所示。图中，DFIG表示双馈异步风力发电机。BESS成本较高且充放电次数有限，许多学者针对该问题研究如何在良好的功率平滑性能基础之上降低电池容量、减少电池充放电次数以及如何保持在适当的荷电状态(SOC)，以降低成本、提高蓄电池寿命。

图1 含BESS的风电系统图Fig.1 Wind power system with battery energy storage system

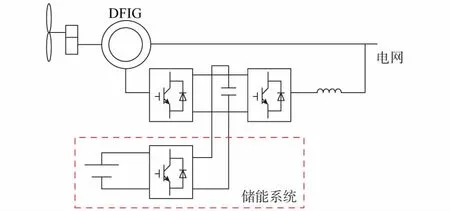
图2 含电池储能的双馈风力发电系统Fig.2 Doubly-fed wind power generation system with battery energy storage

在满足功率平滑度要求的前提下如何兼顾对蓄电池的保护是当前的趋势，也是文献[7]的重点研究所在。文中采用一阶低通滤波器平滑功率，而与常规有所不同的是附加BESS的SOC反馈和功率限幅环节来优化有功功率参考值。BESS的SOC反馈是指实时测量储能系统的SOC，并按照优先级规则调整平滑时间常数，动态调节储能系统充放电功率使其工作在正常区域。功率限幅包含两方面，即输出总功率不超过额定值以及相邻两个控制周期的有功参考值变化率不超过限制值。上述两种控制方法的综合避免了蓄电池工作于过充过放的状态，有效地延长了其寿命。

相比于传统的实时输出功率反馈平滑控制，基于功率预测的平滑控制具有更好的效果，由此，文献[8]提出了一种基于模型预测控制的优化控制方法。结合当前时刻的风电输出功率PW、总输出功率历史数据以及储能系统容量状态，以控制周期内BESS出力最小为目标，计算得到总输出功率目标值，其值与PW的差值作为储能系统输出指令，而PW与BESS实际输出之和为当前的总输出功率。在建立控制系统模型时结合功率波动约束区间和约束软优化策略使得输出总功率满足功率波动平抑指标；采用主动式能量反馈优化控制维持BESS的SOC处在安全区，同时通过动态调整粗糙度惩罚因子进一步地减小输出功率波动幅度。

由于化学BESS可利用寿命较短、成本较高并且其容量与放电功率相关导致其无法满足大规模储能的要求，所以将燃料电池系统作为储能装置也逐渐开始被研究学者重视。燃料电池的基本原理是将外部储存的燃料和氧化剂送入电池中，通过化学反应产生电能向外部输出[9-11]。将传统的比例—积分—微分(PID)控制方法应用于氢氧储能装置调节风速突变时电网侧所产生的功率和电压波动在文献[10-11]所提及。其交流侧变流器通过控制占空比调节存储或者释放能量的大小，控制能量存储速度较快，能够适用于大容量风电场。

目前基于BESS的功率平滑控制除了成本高以外，还存在一些难点，如怎么对电池的SOC估计进行优化，如何优化配置电池储能容量等。针对这些难点，在满足功率平滑要求的前提下，应充分考虑风电功率波动程度、储能系统工作效率、系统功率损耗等因素，以储能容量、储能成本、充放电速率等作为约束条件，将储能系统的投资成本和运行成本作为目标函数，能够有效地协调储能装置容量和经济成本之间的关系。这也将是该类功率平滑方法未来的重点研究方向。

1.2 基于超级电容储能的功率平滑

随着对超级电容研究的深入，将超级电容器替代传统电池用于风电场功率平滑也是目前的研究热点。超级电容基于电化学双电层理论研制而成，可提供强大的脉冲功率，适用于平抑尖峰及往复性风电功率波动。其平滑风电功率原理与蓄电池类似，含超级电容的系统可参照图1和图2，只是将图中电池替换成超级电容。

当前较为普遍的超级电容控制策略是以其电流值为调节对象，如文献[12]所提出的超级电容控制策略如图3所示，其原理是由超级电容器参考功率Psc和电压值Vsc计算并经幅值限制得到电流参考值Isc，该参考值与实际电流值的误差经比例—积分(PI)控制器后与三角载波波形比较，将输出值送入双向降压转换器，对充放电功率进行调节以进行功率平滑。上述方法通过仿真验证了其有效性。

和对蓄电池优化控制类似，也有文献提出基于对超级电容的SOC优化控制进行功率平滑，如文献[13]通过控制蓄电池功率指令的响应频率的初级分配和超级电容SOC模糊控制二次修正实现混合储能内部功率指令的合理分配，在保证储能系统本身安全性的前提下提高了系统的调节特性和运行经济性。文献[14]基于双向DC/AC变换器，通过双闭环控制对变换器内部的电压和电流进行控制，将波动变换较快的电流分量分配给超级电容器以平滑相应分量的功率波动，且研究了基于卡尔曼滤波算法的SOC估计。

图3 超级电容器控制框图Fig.3 Control diagram of super capacitor

由于超级电容能量密度不足导致其不能长时间提供电能支撑，所以当前大多将蓄电池与超级电容两者进行结合构成混合储能系统。针对混合储能协调控制难度较大的问题，可根据风电预测值、电网发电计划等变量预先对各类储能制定好相应的控制策略表，以提高运行控制的可靠性。

超级电容的端电压在功率调节的过程中变化频繁，故须装设必要的装置来维持其端电压稳定。此外，对于超级电容的自放电现象也有必要采取适当的措施加以控制以避免损耗的加重。基于储能单元SOC的超级电容控制在设计时需要考虑电压控制环路由于其带宽过大对功率调节产生的影响，从而保证能量管理模块的有效工作。

1.3 基于超导磁储能的功率平滑

为了替代传统电池的储能装置，超导磁储能系统(SMES)也是目前学者们研究较多的一种新型储能系统，其具有效率高、响应迅速、控制方便、使用灵活等特点。SMES主要由超导磁体、冷却系统、变流器、保护系统等组成。

SMES研究中最关键的部分是SMES数学模型的建立以及控制策略的选择，选取是否得当将决定能否最大化利用SMES的性能。传统的SMES控制方案一般以有功功率、无功功率解耦控制为目标。例如文献[15]，在基于电网侧同步旋转d-q坐标系下，选取SMES安装处的有功功率P和电压U为控制对象，采用网侧电压定向的矢量控制方案，通过网侧电流的d,q分量实现有功和无功功率的独立控制。文献[16]提出了一种用于平滑风电场输出功率的SMES的新型自适应控制方案。论文中SMES仍由传统的电压源型逆变器和DC-DC变换器组成，但控制SMES的自适应PI控制器采用了集合隶属度仿射投影算法，基于该算法的控制策略可以优化SMES的功率平滑性能，避免了由微调控制器参数而带来的影响。

与上述方法中以优化SMES的变换器控制为目标所不同，对SMES整体功率进行调节的直接电源控制(DPC)算法能够有效提高功率平滑响应速度[17]。该算法将直接测量的SMES变流器电压电流值经计算模块得到有功功率、无功功率和相角值，并得出与外部给定的P,Q参考值之间的误差，经滞环控制器给出输出值Sp和Sq。该控制策略框图如图4所示，通过MATLAB/Simulink仿真验证了其良好的平滑性能。

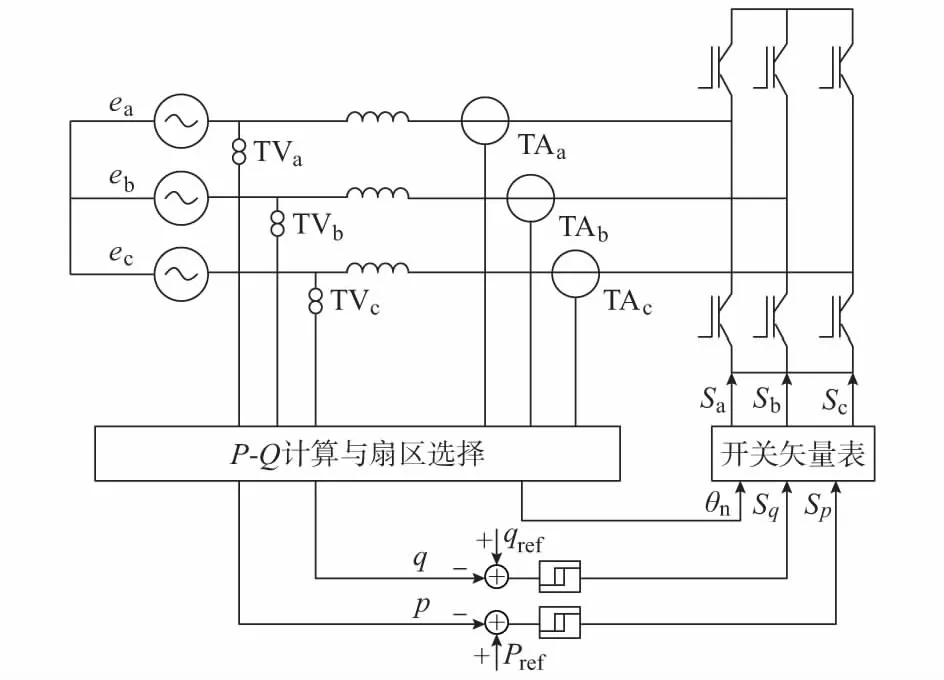
图4 SMES中的DPC算法控制框图Fig.4 Control diagram of DPC algorithm in SMES

尽管SMES的功率平滑特性较好，但其成本太高，且存在低温冷却要求高等问题，离实际应用还尚远。除了与其他储能方式一样要考虑合理的容量配置以及与其他控制系统协调以外，某些情况下还需要针对超导线圈本身的暂态特性建立SMES详细的数学模型。

1.4 基于飞轮储能的功率平滑

在当前众多储能技术中，飞轮储能展示出了相当大的发展潜力和竞争力。相比于传统的蓄电池储能，飞轮储能具有储能密度大、充放电次数不限，充放电时间较快、使用寿命长、对环境污染小等许多优点。采用飞轮储能的风电系统如图5所示。图中，IM表示感应电动机。飞轮储能系统(FESS)主要由飞轮转子、电机、变流器、控制器以及一些辅助设备组成。

FESS工作过程为：飞轮转子与电机转子直接相连，当风电系统输出功率高于给定值时，多余的能量通过变流器提供给电机，电机以电动机形式运行，带动飞轮加速旋转至一定速度，此时电能就转变为飞轮的机械能。当风电系统输出功率低于给定值时，飞轮系统降低速度并作为发电机运行，将机械能转换为电能再经飞轮侧变流器输出至电网。

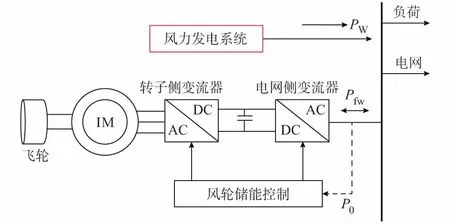
图5 含飞轮储能的风电系统Fig.5 Wind power system with flywheel energy storage

常见的FESS控制方案以功率解耦控制为主，一般采用转子磁链定向矢量控制。文献[18]在传统矢量控制基础之上，加入了改进比例—谐振(PR)控制器。由于传统控制策略为了增强系统的抗干扰能力，加入了电流状态反馈以及电网电压作为前馈补偿，但是其参数在飞轮高速状态时随温度变化而变化，因此利用改进PR控制器可以直接精准跟踪交流量，大大简化了控制算法并避免了参数影响。

当前学者们在考虑功率平滑度要求的基础上力求最有效地利用储能系统容量，由此出现了许多优化控制方案。文献[19]提出了FESS控制方案中的三个制约因素:①风电场并网参数应满足电网规范；②FESS的SOC应适当调整；③调整控制方案以最大限度减少FESS所需容量。由上述指标而设计的FESS控制器包含滑动平均过滤器(SMF)、设定点校正器和速率限制器，如图6所示。SMF的输入为当前实际功率和预测功率值的组合；设定点校正器以SOC作为反馈信号，用以确定总输出功率的设定点；速率限制器是为了确保功率梯度符合电网标准。经过上述三部分的信号处理得到滤波后的所需设定点Pd,ref，减去实际风电场功率Pwf,得到FESS应补偿的容量。上述控制方案经过使用实际风电场数据模拟后证明了其有效性。

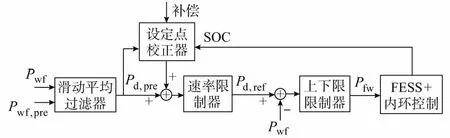
图6 FESS控制器控制框图Fig.6 Control diagram of FESS controller

旨在维持确定的平均SOC的一种新型高级能量管理算法在文献[20]中提出，该控制算法基于PI控制结构的有功功率控制，确保飞轮存储装置的稳定性及期望的时间响应，在使飞轮保持最佳的平均转速的同时用以平滑输出功率的波动部分。基于Lyapunov函数的非线性控制器与传统控制器相比在跟踪功率参考快速变化方面的良好性能使其可以确保系统的渐近稳定性，另外该控制器的调谐不受系统参数和运行条件变化的影响[21]。基于Lyapunov函数的FESS控制拓扑图见图7。风能PW与期望输出到电网的功率之间的偏差量和当前FESS输出功率间的误差作为控制器输入，经过处理后得到FESS的期望输出。经过在MATLAB中的非线性时域仿真验证了算法的有效性。

图7 基于Lyapunov函数的FESS控制框图Fig.7 Control diagram of FESS based on Lyapunov function

目前飞轮储能控制研究中还是大都采用常规控制方式，其应用于工作范围较宽、随机干扰比较大、非线性情况严重的风电系统具有一定的局限性，今后针对此类问题需做出一些改进。例如上文所述的在系统中引入前馈控制虽然有效，但前馈补偿能力有限，可研究新型的智能算法控制，利用其非线性、变结构、自寻优的功能来克服系统的参数时变及非线性因素。另外在飞轮储能控制中必须注意其转速的限制，大多数研究并未考虑转速约束条件，所以后续需要在FESS中增设一个转速控制模块，结合前述的考虑储能SOC方法以及智能算法(例如模糊控制算法)，设计出全面的FESS控制策略。

2 无储能装置的直接功率控制平滑方法

由于附加储能装置进行风电功率平滑会大大增加成本，所以很多学者提出了无储能装置的功率平滑控制方法。

2.1 基于转子惯性动能的功率平滑

利用转子动能的方法其原理是由于转子在转动时存在惯性，所以当转子转速发生变化时，相应地会有能量的释放和存储，将转子动能变为一个虚拟的存储装置在输出功率波动时进行调节。当风速快速增大时伴随发电机加速，将一部分转子动能存储在转子端；当风速快速降低时发电机减速，此时风电输出功率不足，转速减小所释放的转子动能则补偿这部分不足功率。常规基于转子动能平滑功率的控制策略分析如下。

风电机组最大输出功率平均值可以计算为：

(1)

式中：t为实际时间；T为采样周期；Pwopt为风电机组最大输出功率。

最大输出功率和平均功率差值即为须平滑的功率，则转子储存或释放的动能就是该功率差值的积分。转子动能为：

(2)

式中：J和ω分别为转动惯量和角速度。

为了平滑功率，转子参考动能为：

(3)

此时，给定参考转速可得

(4)

基于转子惯性动能的输出功率平滑则可由给定发电机如式(4)所示的参考转速实现,以永磁直驱同步发电机(PMSG)为例的功率平滑控制框图如图8所示。图中，SVPWM表示空间矢量脉宽调制。

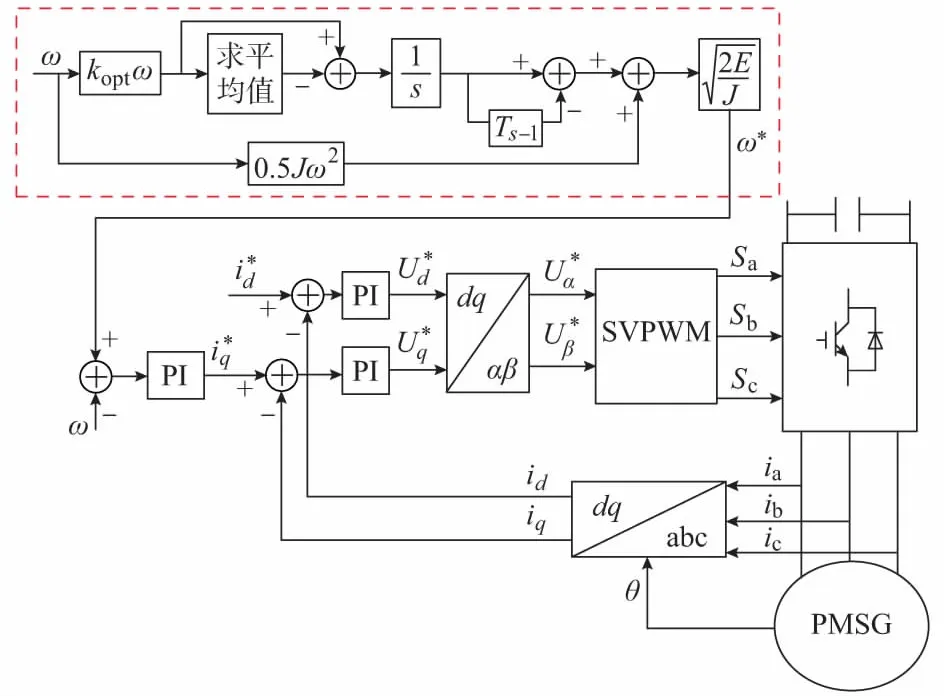
图8 基于转子惯性动能的风电系统控制框图Fig.8 Control diagram of wind power system based on rotor inertial kinetic energy

在传统方法基础上，研究者们开始关注功率平滑与发电效率之间的协调关系。采用基于帕累托前沿的优化协调控制方法以控制发电机转子动能中的能量解决输出功率波动的有效性在文献[22]中得到验证。文中以风电机组的电转矩Te(t)和桨距角β(t)为控制变量,建立基于总输出功率最大化J1和功率波动最小化J2这两个成本函数的加权和的优化问题，上述优化问题由梯度求解器求解，求解结果以帕累托前沿曲线表示，经验证功率波动性得到了有效抑制。

积分补偿控制(ICC)协调算法的提出有效地改善了采用转子动能平滑功率时会导致转子速度偏离最佳值并降低风能捕获效率的问题[23]。ICC应用了一个附加的整体扭矩项，使风电场总输出功率以风电捕获效率损失的边际成本平滑。与提高风电捕获率为目的控制算法相类似，文献[24]提出的新控制方法不仅可以复制最大功率点跟踪控制下的原始功率轨迹，而且能够基于这个轨迹平滑输出功率。文献[25]提出了基于新型模糊控制器的转子动能功率平滑控制策略，使风电场既能输出平滑功率也可以按电网要求输出给定功率。

但是风力发电机转子动能有限，当风能波动较大时很有可能无法满足功率平抑要求。针对此类情况，建议将功率预测技术与转子动能测量装置进行结合，通过预测未来时段的输出功率，提前判断转子转速是否满足功率平抑要求，若满足要求则在下一时段进行操作，若不满足要求则可以采用其他储能方式进行协同调节。

2.2 基于直流母线电压控制的功率平滑

相比于利用转子动能，采用控制直流母线电压进行功率平滑的算法其原理简单也更易于实施操作[26-29]。目前的变速恒频风力发电系统中，发电机与电网间都会通过双脉冲宽度调制(PWM)变换器连接，直流电容位于两个变换器之间。传统的网侧变换器控制直流电压保持恒定，而为了平滑输出功率，可通过改变直流电压的给定参考值。电机侧变流器输出功率Po与经滤波器后的功率Ps之间的功率差表示为ΔPdc=Ps-Po，再假设流经直流电容的电流为idc，那么与此功率波动所对应的直流电容电压变化量为ΔVdc=ΔPdc/Idc，然后将该反映功率波动的量与直流电容给定额定电压相加得到直流电容电压参考值，最后通过相应的控制环节调节功率波动。当前研究所采用的控制策略大多基于该原理，如图9所示。

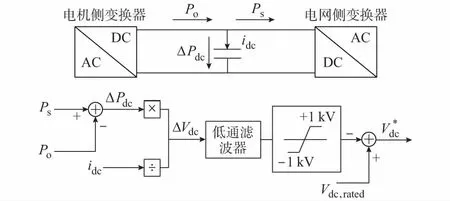
图9 直流母线电压控制原理图Fig.9 Schematic diagram of DC-link voltage control

一种考虑风电场尾流效应的永磁发电机综合功率平滑方案在文献[26]中提出，通过直流母线电压控制系统平滑高频范围内的功率波动。文献[27]提出基于PMSG的直流母线电压和桨距角的协调控制策略，此外在直流环节加入斩波控制电路使得在风力发电系统故障期间仍然实现系统的输出功率稳定。文献[28]中控制算法采用直流电压变步长代替转速定步长，设定直流电容电压偏差量为功率变化量平方的比例值，在风速变化导致输出功率变化时以上述方法得到新的直流电压参考值，经过仿真验证了有效性。

不同于将直流母线电压变化作为参考量，将保持直流电压恒定，同时保持正弦电网电流作为电网侧PWM转换器的控制目标同样可以有效地进行有功功率平滑[29]，控制框图如图10所示。其中Eref和Ef分别为直流母线电压的参考值和反馈值；id,ref和iq,ref分别为直轴和交轴电流的参考值；id,f和iq,f分别为直轴和交轴电流的反馈值；θ为电网电压的相位角；Pgen为发电机的有功功率；C为常量。控制器改变全范围变流器的直流母线电压来平滑由于风电机组的风切变和塔阴影效应导致的三相有功波动。同时为避免控制器干扰风力涡轮机的速度控制，发电机的有功功率信号在输入前需要用带通滤波器(BP)进行滤波。

图10 网侧PWM转换器控制框图Fig.10 Control diagram of grid-side PWM converter

由于直流母线电压在功率平滑时其电压幅值越限时，风力发电系统的最大风能跟踪能力会下降，所以须在控制中加入电压幅值限制模块，同时这也将限制直流电压平滑输出功率的能力。另外考虑到直流电容与其他器件之间存在耦合影响，所以参数设置时也都需留有裕度。

2.3 基于桨距角控制的功率平滑

变桨距是通过控制技术和动力系统调整桨叶的桨距角，即调整叶尖弦线与风轮平面的夹角，从而改变桨叶的升力和阻力；而变桨距控制技术是指根据当前风速和转子转速调整叶片桨距角，从而调节风电机组的输出功率。传统的变桨距控制都是当风速低于额定风速时，桨距角控制不工作；当风速超过额定风速时，切入桨距角控制，基于PI控制器对桨距角进行调节从而使输出功率始终保持在额定功率，故额定风速以上时已实现功率平滑控制。

而基于桨距角的功率平滑方法是要在额定风速以下时也引入桨距角控制，实现全风速的输出功率平滑。文献[30]通过桨距角控制对工作区域所有风电机组输出功率进行调节，采用了基于平均风速以及风速和桨距角标准偏差的控制策略。首先俯仰角G(β)的控制量由式(5)给出,即

(5)

式中：β为桨距角；A1和A2分别为与桨距角相关的二次函数；ΔP和Δβ分别为实际输出功率Pg和β的小信号状态变量，式(5)的值取决于风速VW；α12，α13，α14,α22，α23，α24为常数。

图11为桨距角指令βCMD的桨距角控制系统，e为输出功率指令Pgo与实际输出功率Pg间的差值，由比例—微分控制器的输出功率信号ΔP以及G(β)的乘积决定桨距角变化量Δβ，其值与β相加最后得到桨距角指令βCMD,Table 2D表示对应输入VW和β的输出G(β)数据列表。

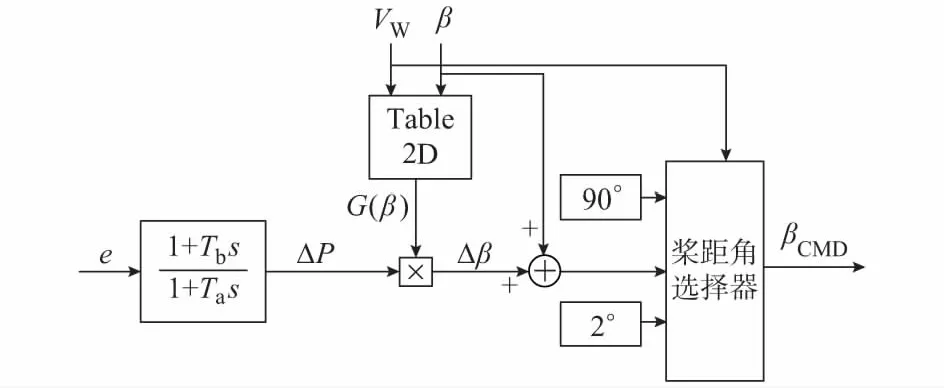
图11 桨距角功率平滑控制系统框图Fig.11 Block diagram of power smoothing control system of pitch angel

由于在桨距角为2°时,风电机组捕获能量最大，此时将输出功率指令Pgo替换为固定桨距角为2°，为了能够平滑输出功率指令，新的输出功率命令Pgo为：

(6)

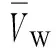
由于Pgo随着瞬时风速变化而波动，而Vσ是风速标准偏差，它表征的是瞬时风速与平均风速间的差值，通过式(6)的计算能更好地避免采用瞬时风速所带来的输出功率指令波动较大的问题，从而平抑输出功率波动。

近年来对桨距角控制的改进主要体现在控制器的算法优化。文献[31]运用模糊逻辑控制理论进行变桨距，在保证更好的功率平滑性能的同时尽可能提高风能利用率。该控制器由两个相互排斥的模糊逻辑控制系统组合控制，即模糊逻辑系统A和模糊逻辑系统B。模糊逻辑系统A的设计策略是在风速高于额定值时，防止发电机转速超过限速值。而在风速低于额定值时，模糊逻辑系统B进行工作，此时为了平滑风电波动，提出了一种通过产生桨距角指令来并入模糊逻辑系统B的策略。该策略是根据风力波动和功率限制动态选择输出功率目标值。经验证上述两部分控制器的结合可有效平滑输出功率波动。

文献[32]提出了基于增强型Elman神经网络(EENN)的桨距角控制器，其采用渐变下降算法进行在线训练，网络学习使用特定粒子群优化算法进行。在MATLAB中对提出的控制器性能进行了良好的性能验证。一种使用指数加权平均滤波方法(EWMA)的新的桨距角控制系统在文献[33]中提出，该方法对应于俯仰角控制器命令信号的风电机组输出参考值由在线功率的指数加权平均值EWMA确定。在使用EWMA的情况下，由于使用最新的数据时附有较高的加权因子，故可以从平滑的风电机组输出参考值中获取更好的信号。

纵观当前变桨距控制实际中大多以传统控制为主，若将某段时间整定的参数应用于全风速发电过程中则会导致控制效果差。而且由于风电机组的惯性和延迟，且桨距角变化速度有限，会导致系统较长的调节时间和较大的超调量，使机组输出功率波动频繁对电网造成较大冲击。所以应该结合智能新型算法，利用其自适应、优化性能强等特点提高桨距角控制器的鲁棒性。且单单依靠桨距角控制平抑输出功率波动效果仍有限，须寻求与其他功率平滑控制策略协调合作的方法以达到理想的功率平滑效果。

3 各类功率平滑方法总结

每种功率平滑控制方法都有其特点和优缺点，在实际问题中选择功率平滑方法时应结合目标风电机组、风电场及当地电网的实际情况。

基于存储装置的间接功率控制方法虽然可以提供有效的功率平滑，但是需要增加系统的额外成本。表2总结了各类储能技术的特点。超导磁场储能反应迅速，可循环次数较多，放电时间很短所以适用于瞬时平滑功率，但其成本较高。燃料电池储能在充放电过程中响应速度很快，特别适用于兆瓦级风力发电系统，但由于燃料电池系统使用寿命较短，设备损耗较大，并且配置容量受到限制，导致其不能广泛运用。BESS能量转换效率较高、能量密度高、功率吞吐能力大但是其容量受限并且使用寿命较短限制了该储能方法的发展。FESS储能密度大、充放电速度快、占用体积小且对环境无污染的特点使其有较好的发展前景，但由于飞轮的转速限制导致其储能容量受限，且成本较高。

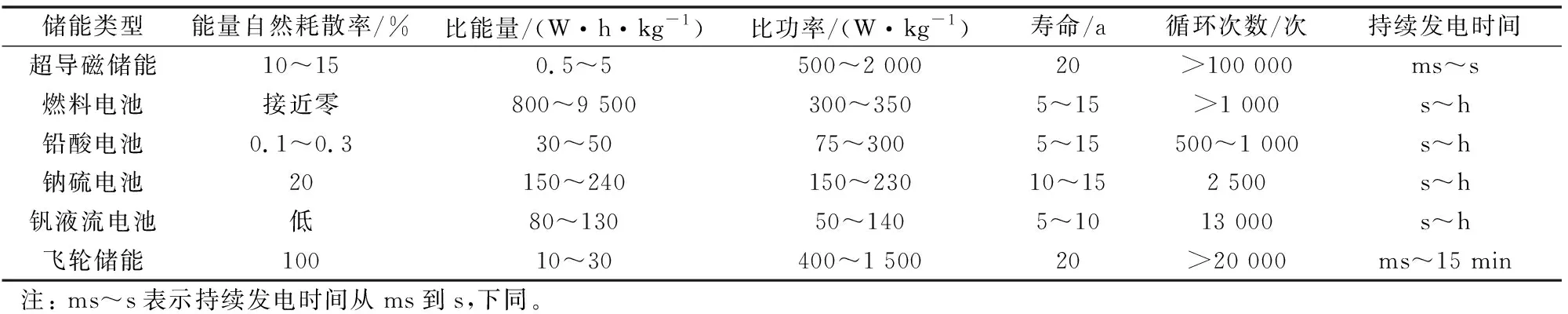
表2 各类储能系统特点比较Table 2 Feature comparison of various energy storage systems

无储能装置的功率平滑方法无须附加额外成本，文献[34]总结对比三种方法的功率输出性能和平滑性能，如图12所示。桨距角控制方法和直流母线电压控制方法虽然都可以实现功率的平滑输出，但相比传统的最大功率跟踪法，这些方法会降低输出功率，这种功率平滑效果无法满足要求。而转子惯性动能控制方法在拥有良好的功率平滑性能的基础之上同时能保证其输出功率不会降低。另外，由于桨距角控制工作于所有风速区域，因此会显著增加风力涡轮机的叶片应力，加重磨损。直流母线电压控制会对直流母线电容产生压力，可能会缩短电容器的使用寿命。上述影响因素使得这两种方法的适用性较低，综合平抑效果低于转子动能控制方法。

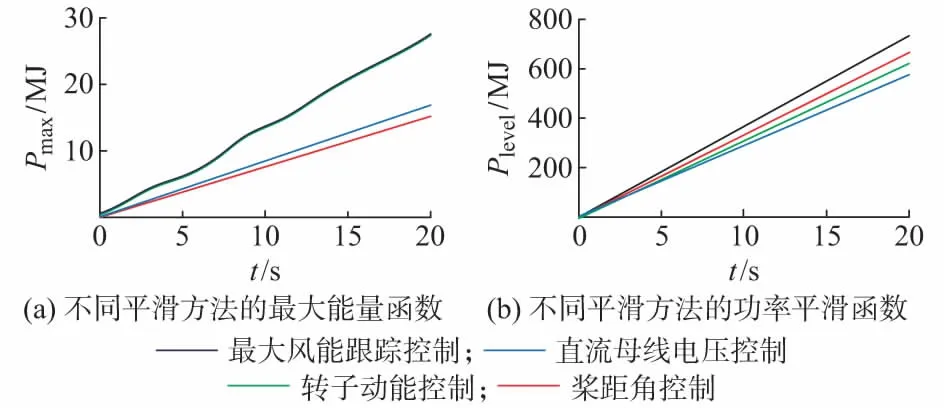
图12 不同平滑方法的最大能量和功率平滑函数Fig.12 Maximum energy and power smoothing functions of different smoothing methods

4 结语

本文对传统和新型的两大类功率平滑方法做了详细的分析，对各类方法所采用的控制策略进行了深入的研究和总结归纳，对存在的问题提出优化建议，为风电场选取适当的功率平滑方法提供了技术参考。储能装置中由于蓄电池系统、燃料电池系统体积大，超级电容、超导储能技术成本过高等因素限制了其发展。而随着新型材料电池的研发，这一困境有望在未来得到解决。FESS由于其良好的特性受到了国内外很多学者的研究，随着其技术的成熟，也有望大规模应用于风电场。在无储能的功率平滑控制方法中，基于桨距角控制和直流母线电压控制会降低风电场输出功率，所以从风电场输出功率效率来看,基于转子惯性动能的控制要优于上述两种方法。但是此类功率平滑方法均针对单一风力机进行控制，对于由很多台风电机组成的大型风电场而言，平滑控制效果较弱。

综上，主流的两类风电场功率平滑技术均有其优缺点，且目前尚无法克服这些缺点。因此，学者们也开始从风电场各风力机调度控制的角度去研究功率平滑控制，既无需储能装置，也可以从风电场整体输出功率为出发点改善平滑控制效果。随着传统功率平滑控制技术的逐渐成熟以及新型技术的不断涌现，各类功率平滑方法将有望大规模用于改善风电场的运行特性，从而实现替代传统化石能源的目标。