利用重复控制跟踪的统一潮流控制器抑制系统强迫振荡方法

蒋 平, 陈 琼, 吴 熙, 蔡 晖, 祁万春, 谢珍建

(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 国网江苏省电力有限公司电力经济技术研究院, 江苏省南京市 210096)

0 引言

随着现代电力系统规模的不断扩大、可再生能源的广泛接入以及多种新型调控装置的投入使用[1],电网中发生强迫低频振荡的次数逐渐增多[2],使得强迫振荡成为影响电力系统安全稳定的关键问题之一。开展强迫振荡理论分析,寻求其针对性抑制方法具有重要意义。

相关文献指出,强迫振荡的起因是系统受到周期性扰动,其振幅与系统阻尼负相关[3],且振荡随扰动源消失而迅速衰减[4-5]。针对上述特性,目前研究学者提出了一些针对强迫振荡的抑制措施。通过在线获取全网运行数据[6]、本征分析和包络线拟合等技术[7],可以辨识定位强迫振荡扰动源,并予以切除。但目前辨识定位技术还在发展阶段,准确性和时效性无法保证。此外,一些学者提出装设电力系统稳定器(power system stabilizer,PSS)[8-10]或静止同步串联补偿器(static synchronous series compensator,SSSC)、统一潮流控制器(unified power flow controller,UPFC)等柔性交流输电系统(FACTS)设备提高系统阻尼[11-12],但强迫扰动源持续向系统注入扰动功率,这类方法仅能减小振荡幅值,无法完全抑制强迫振荡。文献[1]在发电机励磁系统中采用自抗扰技术与非线性综合控制方法,通过分散本地控制从而抑制系统强迫振荡,提供了一种新的抑制方法和思路。但该方法中状态观测器负担重,参数选择困难。

针对强迫振荡扰动源的周期性特征,本文考虑在振荡抑制中引入重复控制技术。重复控制属于内模原理[13]的一种,理想情况下,当系统受到的干扰为已知频率周期信号,重复控制可以对系统参考值进行较为准确的跟踪[14]。重复控制目前在伺服定位及逆变谐波控制领域有广泛运用。文献[15]利用重复控制来应对数字视频光盘(DVD)循轨伺服系统中的盘片偏摆问题,有效抑制了已知频率的周期干扰信号。文献[16]利用重复控制使电力滤波器补偿由非线性负载引起的谐波失真,取得了较好的效果。但以上方法均利用重复控制做信号跟踪,暂未将其应用于振荡功率抑制的分析研究。受到强迫振荡扰动时,重复控制能够较好地跟踪系统稳态参考值,但其自身不具备功率输出能力,需结合一种能够调节系统有功、无功功率的器件作为载体,实现抑制振荡功率的目标。

因此,本文提出一种利用重复控制跟踪的UPFC抑制强迫振荡方法。通过重复控制的内模原理跟踪系统功率稳态参考值,使UPFC输出满足要求的抑制功率,从而有效抑制系统强迫振荡。

1 UPFC抑制强迫振荡原理

1.1 电力系统强迫振荡原理

在单机无穷大系统中分析电力系统发生强迫振荡的情况,求解此时发电机转子运动方程组,可知其功角δ的变化情况[3]为:

(1)

根据式(1)绘制不同系统阻尼比下,功角变化量幅值与扰动源角频率ωd之间的变化关系,此处假设常量Γ=1(标幺值),K=1,ωn=4.65 rad/s,如附录A图A1所示。分析图A1曲线变化情况可得到以下结论:①ωd与ωn越接近,强迫振荡越严重;②通过增大系统阻尼系数,可以使强迫振荡幅值减小。理论上当系统阻尼比趋于无穷大时,功角变化量趋于0,系统强迫振荡可以完全被抑制,但实际情况下,系统阻尼比不能无限增大。文献[17]指出,对于一个电力系统,其状态方程特征根实部之和为常数,故系统中各模式的总阻尼恒定。如果为抑制某一频率强迫振荡而增大该机电模式阻尼,则必将减少其他机电、非机电模式的阻尼,引起其他模式的低频振荡或非机械变量的大幅波动。此外,随着阻尼比增大,提高相同大小的阻尼比能够降低的振荡幅值越来越小,此时继续通过增大阻尼比来抑制强迫振荡将越来越困难。上述分析表明,增加系统阻尼能从一定程度上降低强迫振荡幅值,但受限于实际情况,不能仅依靠该方法,还应从其他方向寻求针对性的抑制方法。

1.2 UPFC动态性能分析

UPFC能快速调节线路潮流和控制节点电压,其动态调节作用还可改善系统的暂态稳定性能。为进一步分析其动态调节机理,在单机无穷大系统中接入UPFC电源模型,并用电压源和电流源分别代表UPFC的串联侧和并联侧,如附录A图A2所示。

接入UPFC后,其注入功率将使得线路潮流发生变化。此时UPFC所在线路上流过的有功功率Pij可以写成:

(2)

式中:VΦ=Vsesinθse;Iχ=Iccosθc;各变量含义参见附录A图A2。

类似的,此时UPFC所在线路上的无功功率可以写成:

(3)

此外,由UPFC内部控制结构可知,其动态性能受到串并联侧比例—积分(PI)控制器影响。以线路有功潮流Pij为例,注入量VΦ和Iχ与线路功率偏差存在以下关系:

(4)

式中:Ksep和Ksei分别为串联侧用于控制VΦ的PI控制器的比例、积分增益;Kcp和Kci分别为并联侧用于控制Iχ的PI控制器比例、积分增益。

将上式线性化,可得:

(5)

将式(2)—式(5)与发电机转子运动方程联立,可得到接入UPFC后系统线性化模型以及传递函数框图,如图1所示,其推导过程和参数说明详见附录B。

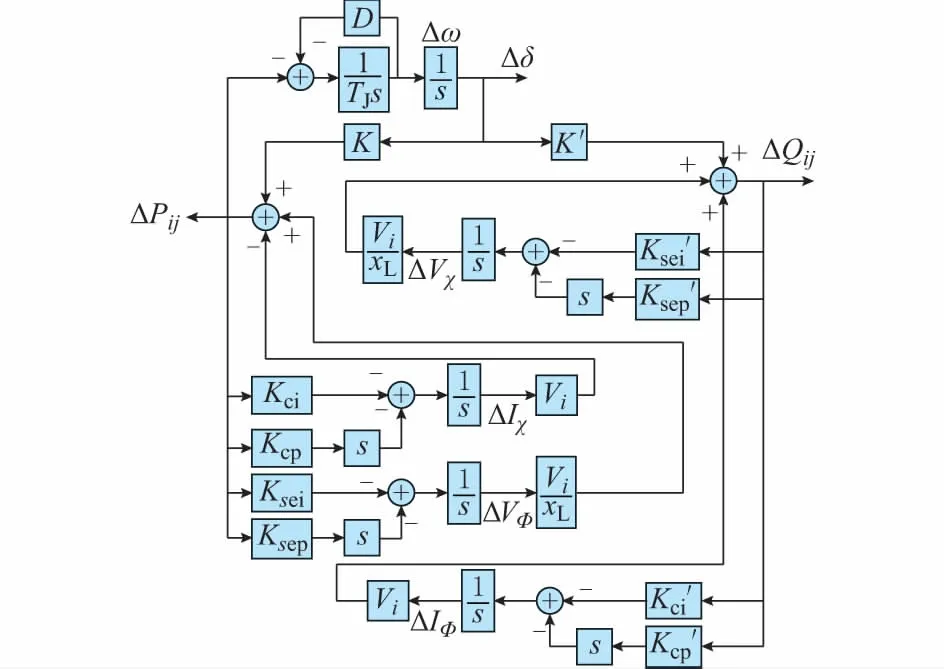
图1 含UPFC的系统传递函数框图Fig.1 Block diagram of system transfer function with UPFC

由图1可见,UPFC的动态调节作用改变了系统线性化模型。因此,在参数合适的情况下,能够提高系统阻尼,抑制强迫振荡,但由1.1节分析与后文第4节仿真算例可知,仅依靠提升阻尼抑制效果不够理想;式(2)和式(3)表明,UPFC通过等效注入功率能够调节系统潮流,因此本文从功率调控角度,结合重复控制方法,提出了一种进一步抑制强迫振荡的策略。

2 重复控制抑制强迫扰动信号方法

2.1 理想重复控制简介

重复控制是根据内模原理提出的一种新型控制方法:如果某一信号可以视为一个自治系统的输出,将这一信号的模型设置在稳定的闭环系统中,则反馈系统可实现对此信号的完全跟踪或抑制[18]。理想重复控制内模如附录A图A3所示,可推得其基本环节的传递函数如式(6)所示,其中e-sT是一个纯延时环节。

(6)

当外部输入一周期为Td的干扰信号,令纯延时环节中的参数T=Td,此时闭环回路内经过延时可以产生输入信号的内模。因此,采用此重复控制内模,理论上能够无稳态误差跟踪系统参考值,抑制强迫扰动源产生的周期振荡信号,在下一小节将通过进一步论证推导予以证明。

2.2 插入式改进重复控制抑制强迫扰动性能分析

重复控制内模的时滞正反馈回路可以利用前一周期的控制量与当前时刻的误差量修正下一周期控制量,以实现控制目标。理想情况下,其延时环节参数T与外部强迫扰动信号周期Td相等时,抑制效果较好。而此时极点恰好位于虚轴上,系统处于临界稳定状态[14],对参数准确性提出了很高的要求,稳定性和可控性较差。

为弥补这一缺点,本文在理想重复控制内模环节基础上引入修正环节B(s),使重复控制器极点略微偏离虚轴,在尽量不牺牲抑制能力的前提下改进其稳定性能。考虑到系统所受强迫扰动源属于低频振荡,该修正环节对于重复控制低频段极点的偏移不应过大,因此设计为形如1/(κs+1)的一阶低通滤波器(LPF)。

在接入实际控制系统时,为减小对原系统的影响,本文在原有控制结构的基础上,通过并联相加来接入重复控制,保证了二者的相互独立,实现简单。上述系统结构,在下文统称为插入式改进重复控制 (plug-in modified repetitive control,PMRC),其接入控制系统后的传递函数框图如图2所示。其中R(s)表示输入参考值,在本文讨论的控制模型中选用线路功率稳态基准值;Y(s)表示系统输出值,选用线路功率实际值;D(s)表示外部周期性扰动源,即已知振荡周期Td的强迫扰动源;G(s)表示原被控系统的传递函数;E(s)表示被控对象误差。

图2 PMRC结构Fig.2 Structure of PMRC

图2所示PMRC结构的控制关系方程为:

(7)

联立并消去中间变量,为便于分析,此处先将B(s)取为1,可得

(8)

设强迫振荡扰动源D(s)角频率为ωd=2π/Td,令s=jωd,T=Td,此时有

(9)

将式(9)代入式(8)可得:

(10)

由上述分析可知,对于频率为ωd的强迫扰动源,当PMRC中变量T=Td,B(s)=1时,理论上能够实现系统的零稳态误差跟踪,完全抑制该强迫振荡信号。此时C(s)的极点分布如附录A图A4中黑色标记所示,均位于虚轴上(假设扰动源频率为1.35 Hz,ωd=8.48 rad/s)。

当B(s)≠1,按上文分析将其设计成1/(κs+1),C(s)为:

(11)

将式(11)用欧拉方程展开,并在ω=ωd处取其模:

|C(jωd)|=

(12)

当κ取得较小,且ωd处于低频段,C(s)的模在其最大值附近,代入式(8)所示误差表达式后,式(10)仍可近似成立;高频段C(s)的模逐渐减小,误差增大。假设常量κ取0.000 6,此时C(s)极点如附录A图A4红色标记所示,低频段与黑色标记几乎重合,高频段略微偏离严格位于虚轴上的黑色标记。整体上B(s)=1与B(s)≠1的极点重合度很高,与前述理论分析一致。由于强迫低频振荡一般发生的角频率范围为0.628～15.7 rad/s,而PMRC在低频段可以输出较为准确的内模,因此只要κ在可选范围内取得尽量小,B(s)的引入在增强系统稳定性的同时,对强迫振荡的抑制效果影响不大。为保证系统稳定和低频段有效覆盖振荡频段,B(s)中κ需满足式(13)和式(14),其具体推导过程见附录C。

(13)

(14)

3 采用重复控制和UPFC抑制强迫振荡的控制器实现

上文讨论了PMRC对强迫扰动源信号的抑制能力。实际应用时,强迫振荡向系统中持续注入功率能量,而PMRC自身不具备功率调节功能,仅依靠其控制环节无法抑制系统功率振荡。因此,本文提出由PMRC跟踪系统稳态参考值,结合UPFC作为功率输出载体,从而抑制强迫振荡。

具体的结合方式如图3所示。其中Pref和Qref对应R(s),Pij和Qij对应Y(s);而扰动一般发生在系统内部,系统响应出的强迫振荡直接体现在线路功率Pij和Qij中,因此在控制器中未标出D(s);与附录B图B1相比,UPFC本体控制器中的PI控制器、后续换流器控制器保持不变;虚线框内的框图即PMRC,分为两路,分别安装在UPFC有功和无功控制回路,通过一个相加环节加入功率比较点和原控制系统之间,不影响PI控制的前向通道,以减小对原控制系统的干扰。

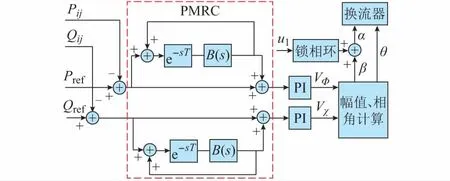
图3 基于PMRC的UPFC控制结构Fig.3 Structure of UPFC based on PMRC

选取参数时,应首先通过广域测量系统(wide area measurement system,WAMS)获取线路振荡信息,利用总体最小二乘—旋转不变技术(TLS-ESPRIT)算法从中提取强迫振荡频率ωd,并计算出相应Td,由此初步确定PMRC中延时环节的参数T。为减小对C(s)极点位置的影响,B(s)中κ应在满足2.2节系统稳定和频率覆盖条件的情况下取得尽量小。最后,根据实际仿真效果对T和κ进行微调,以达到较为理想的控制效果。

4 算例分析

4.1 案例1

本文首先在一个等值双机系统中验证所提方法的有效性,其系统结构如附录A图A5所示,经小扰动分析可知,系统固有振荡频率为1.35 Hz。UPFC装设在母线B2与B3之间,其潮流控制目标设定为原系统稳态潮流,各PI控制器增益按典型参数值整定;未投入时,B2与B3直接相连。

由于发电机功率波动引起的强迫振荡较其他扰动源更严重,因此在G1调速器出口施加频率为1.35 Hz、幅值为0.1(标幺值)的正弦机械功率扰动,其表达式为d(t)=0.1sin(2π×1.35t),针对不含UPFC、仅含UPFC、基于PMRC的UPFC、基于传统附加阻尼的UPFC这4种情况分别进行仿真,结果如图4所示。其中传统附加阻尼参数按相位补偿法整定。

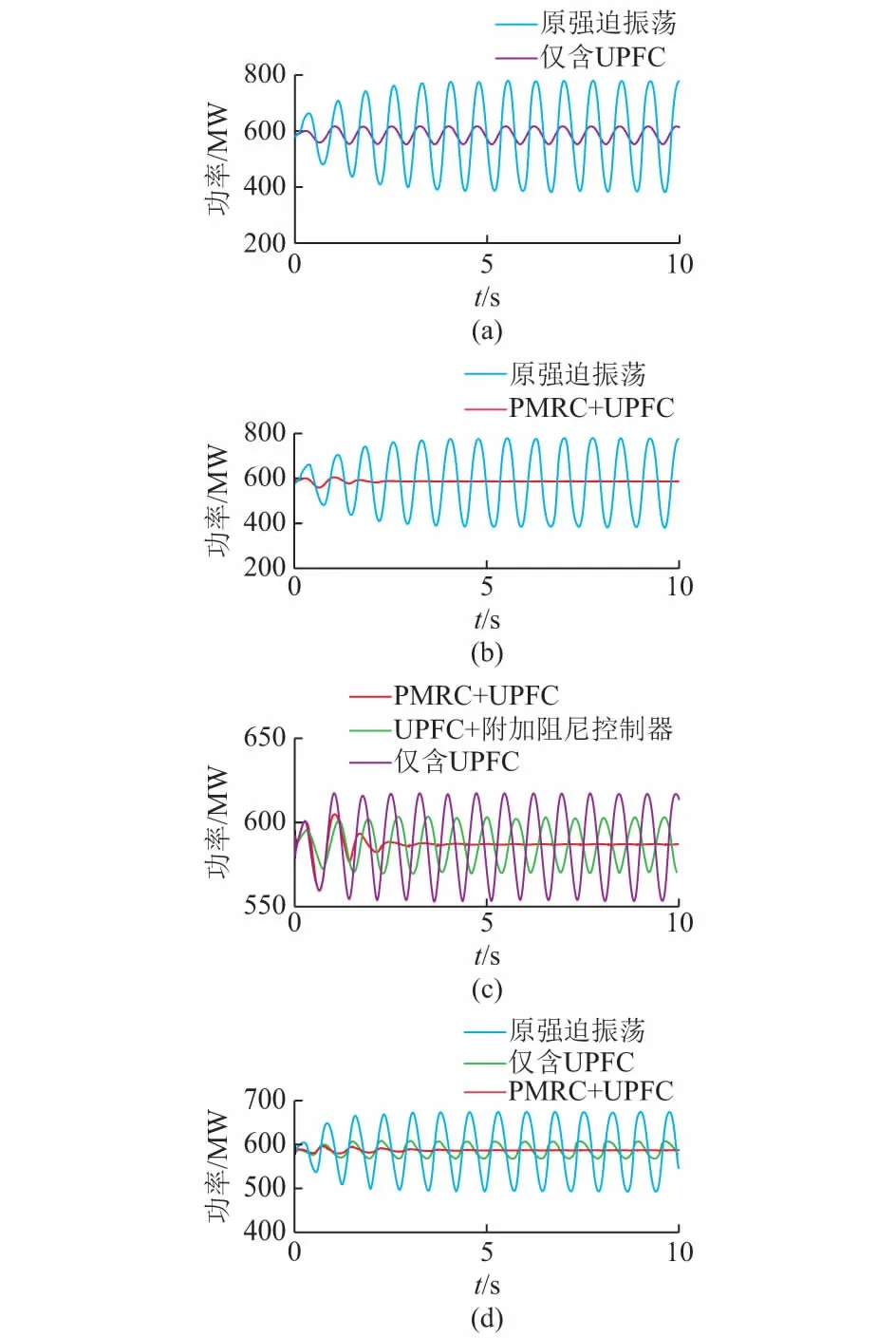
图4 双机系统强迫振荡情况Fig.4 Forced oscillation in two-machine power system

由图4(a)可知,UPFC的动态调节作用增强了系统阻尼,减小了强迫振荡幅值,但效果不够理想,无法完全抑制强迫振荡。在此基础上,按第3节所述设计方法确定PMRC参数,加入基于PMRC的UPFC,结果如图4(b)所示。UPFC提供了更高的阻尼,强迫振荡幅度进一步减小,且系统中响应的振荡几乎被抑制到平息。可见,基于PMRC的UPFC不但能够通过提高系统阻尼大幅降低起振幅度,且可以按PMRC跟踪系统参考值的要求,根据扰动源的波动频率特点,主动输出补偿性质的抑制功率,使强迫振荡得到有效抑制。

从图4(c)仅含UPFC、本文所提方法以及传统附加阻尼控制方法的对比可以看出,附加阻尼超前滞后环节的补偿作用通过提高系统阻尼略微改善了仅含UPFC控制器的抑制振荡性能,但本文所提基于PMRC的UPFC由于准确跟踪系统稳态参考值,并输出抑制功率,产生了更好的抑制效果。

为验证本文所提方法对不同类型扰动源的抑制效果,将前一例中的机械功率扰动源改为励磁扰动源。在G1励磁输入值上施加频率为1.35 Hz、幅值为0.1(标幺值)的正弦扰动,其表达式为d(t)=0.1sin(2π×1.35t),针对不含UPFC、仅含UPFC以及基于PMRC的UPFC控制这3种情况分别进行仿真,结果如图4(d)所示。

由图4(d)可见,同样大小的励磁扰动引发的系统强迫振荡幅值小于机械功率扰动,因此在实际中机械功率扰动源更需受到重视。在投入UPFC时,能够初步抑制强迫振荡振幅;而在PMRC与UPFC共同投入时,UPFC能输出补偿功率,使系统振荡逐渐平息。上述仿真证明了本文所提方法对机械功率扰动和励磁扰动引发的系统强迫振荡均能产生较好的抑制效果。

4.2 案例2

220 kV南京西环网UPFC工程是中国第一个UPFC工程,实际安装地点位于晓庄—铁北双回线路[19],采用该系统结构进行实际电网仿真验证。其工程主回路如附录A图A6所示。

其中,华京电厂容量为2×320 MW,金陵燃机容量为2×390 MW,将含有PMRC的UPFC安装在晓庄—铁北之间,UPFC自身容量为串联侧120 MVA,并联侧60 MVA,未投入UPFC时晓庄与铁北以双回线直接相连。现在华京电厂一台发电机的调速器出口施加频率为1 Hz、幅值为0.1(标幺值)的正弦机械功率扰动。分别针对未投入UPFC、投入含有PMRC的UPFC这2种情况进行仿真,选取铁北站观察控制器对系统强迫振荡的抑制效果,结果如图5(a)所示。

从仿真结果可以看出,本文所提控制器能够较好地跟踪线路功率稳态参考值,并在每个扰动周期输出对应的补偿功率。此时UPFC容量仅占该区域发电机总容量约10%(功率因数按0.98计),仍能够有效抑制周期性扰动源引发的系统强迫振荡。

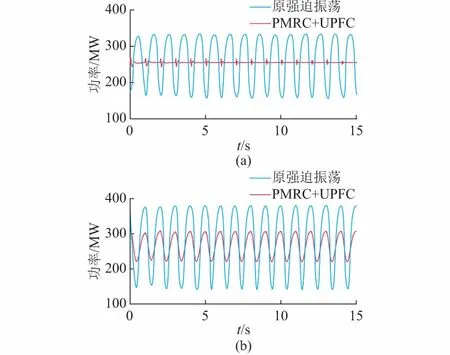
图5 南京西环网强迫振荡情况Fig.5 Forced oscillation of Nanjing West Ring Network

改变扰动源施加的位置,在距离UPFC安装位置较远的金陵燃机一台发电机的调速器出口施加同样的扰动,观察铁北站抑制效果,结果如图5(b)所示。由于扰动源与UPFC之间电气距离较远,因此该控制器对系统强迫振荡的抑制效果不够好。综上所述,在实际情况中为更好地抑制强迫振荡,应尽量使UPFC靠近扰动源所在区域或发电机。

该仿真案例表明,本文所提基于PMRC的UPFC控制方法能够有效抑制实际电网中的强迫振荡,且UPFC的安装位置距离扰动源越近,抑制效果越好。

5 结语

本文从强迫振荡特性出发,分析了UPFC提高系统阻尼、抑制强迫振荡的机理;设计了适用于抑制强迫扰动、有效跟踪系统稳态参考值的PMRC;进而提出使UPFC按PMRC跟踪性要求输出抑制功率的方法。仿真结果表明,该方法对系统强迫振荡的抑制效果优于仅采用UPFC或采用UPFC与附加阻尼控制器的控制方法。需要指出的是,在UPFC与扰动源距离较远时,抑制效果不够理想。下一步,可考虑结合实际情况,探究新的技术手段,就距离对抑制效果的影响问题展开进一步研究。

本文研究得到国网江苏省电力有限公司科技项目“500千伏UPFC接入苏州南部电网控制策略深化应用研究”的资助，谨此致谢！

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。