基于Dijkstra算法的电网故障行波定位方法
李泽文, 唐 平, 曾祥君, 肖仁平, 赵 廷
(长沙理工大学电网安全监控技术教育部工程研究中心, 湖南省长沙市 410114)
0 引言
自1993年全球定位系统(GPS)技术全面民用化以来,其高精度时钟功能使行波定位与保护技术取得了很大进展[1-3],行波技术理论研究日趋成熟[4-6]。然而随着电力网络互联的迅速发展,其结构日益扩大,基于单根线路的行波定位方法不再满足电力网络运行的要求。由于远程通信技术和高精度时间同步技术的提高,根据广域数据建立电网故障行波定位系统,综合利用多点故障行波信息的电网行波定位方法成为故障定位技术的研究热点[3]。
为提高故障行波定位的可靠性和精确度,克服单条线路故障行波的不足,国内外学者针对电网故障行波定位技术从多方面展开研究[7-9]。文献[10]提出基于整个输电网的电压行波故障定位算法,采用全网变电站时间信息的融合处理和容错分析,可在定位装置故障、启动失败或时间记录错误时仍能实现定位精确性。文献[11]融合输电网的全部有效时间数据进行折算等处理后,能较好克服电网中有一台定位装置发生故障或记录错误的时间数据造成的故障定位失败问题。文献[12]提出了将电网的拓扑结构信息和初始行波到达时间进行联合处理和容错分析的区域电网定位新方法,无须依赖断路器状态信息就能克服电网中有一台定位装置发生故障或记录错误的时间数据造成的故障定位失败问题。文献[13]分析电网结构图中电网对象之间存在的告警关联关系来构建对应网络依赖图的故障定位方法,先利用所有站点时间信息直接找到故障线路,再分析图中最优有序并对计算故障点所在位置。文献[14]进一步优化配置定位装置,只选择一部分变电站安装故障定位装置实现观测每条输电线路, 该方法可减少配置数量,节省投资成本。这些研究成果在网络结构简单的电网中可以得到比较好的故障定位结果,但在电网结构比较复杂,尤其是多环网结构时,难以有效简化电网结构,在特殊故障位置下可能出现较大的故障定位误差。
为避免传统网络定位方法中对于复杂环网进行的解网运算,本文提出了一种基于Dijkstra算法的电网故障行波定位方法。该方法利用Dijkstra算法来计算最短路径,无须对环网进行解网运算,同时还可有效提高网络定位的可靠性与准确度,有望促进网络故障定位的实用性。
1 Dijkstra算法基本原理
Dijkstra算法是求取网络结构中任意两节点最短路径问题的一种经典算法,在计算速度、稳定性、工程实现能力等方面具备明显优势[15-16]。把网络图中每个点vi给予两个标号(P(vi),λi),其中P(vi)代表从起点v1至vi的最短路径的长度,而v1至vi的最短路径上vi前一个节点下标是λi,用来标记路径[15]。起初默认网络中全部节点都是未标记点,用临时标记点定义与最短路径中的节点相连接的节点,算法由近及远依次在临时标记点中计算离源节点最近的节点,作为永久标记点,直到所有节点全标记为永久标记点或者寻到了目标。
算法适用于权数非负的边,假设G=(V,E,W)(V为节点集;E为边集;W为权重)是n阶简单带权图,wij≥0 。若vi与vj不相邻,令wij=∞,求G中v1到vn的最短路径,定义如下。
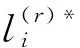

3)pr={v|v已获得的p标号}代表第r步时的通过集。
4)Tr=V-Pr代表第r步时的未通过集,其中r≥0。
由上述定义,Dijkstra算法具体实现步骤如下。


步骤3:判断Tr,若Tr=∅,则结束;否则,转到步骤4。
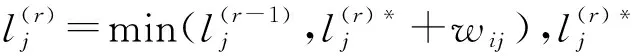
电力系统在忽略电网元件的参数特征的前提下,电网可以拓扑成无向带权图,将电网各变电站设为节点,母线和支路抽象为边集,边的长度设为权值,且权值均为正。Dijkstra算法可以准确求取电网拓扑图中各个节点之间的最短路径,无需解网运算。而电网故障行波的初始传播路径是与最短路径相关联的,二者结合便可实现故障定位。
2 基于Dijkstra的电网故障行波定位算法
2.1 定位原理
电网某条输电线路故障后,检测记录故障初始行波到达所有变电站时间,根据断路器状态信息辅以继电保护动作信号判别故障线路;然后利用Dijkstra算法计算最短路径,建立最短路径距离矩阵,最后将最短路径和相应的故障初始行波到达时间相结合计算故障距离,步骤如下。
1)依据电网结构构建行波定位网络。
2)故障发生后根据断路器动作判别故障所在的线路,并采集全网故障初始行波到达所有变电站时间信息,建立时间矩阵T为:
T=[t1t2…ti…tn]
(1)
3)利用Dijkstra算法计算最短路径,建立最短路径距离矩阵L。
4)修正最短路径距离矩阵L中的元素,得到计算矩阵L′。
5)逐一将计算矩阵L′中的元素,与时间矩阵T相对应的时间代入双端定位公式得到故障距离为:
(2)
式中:dij为节点i与j之间最短路径线路上故障点离节点i的距离;Lij为节点i与节点j之间最短路径所途经路线的长度总和;v为初始行波在输电线上的传播速度。
选取故障线路一端节点c为参考节点,将所有dij折算到参考节点,得到折算故障距离为:
dij′=|dij-dic|
(3)
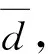
(4)
式中:α为误差门槛值,一般取500 m。

7)对故障距离矩阵D的所有非0有效元素赋予权重,假设故障距离矩阵D的各有效元素对应最短路径上有m个变电站,则可设置该元素的权重为 1/(m-1),得到权重矩阵W。
8)综合故障距离矩阵D和权重矩阵W,计算出精确的故障距离为:
(5)
式中:Wij为故障距离矩阵D中有效元素dij′的权重。
2.2 最短路径求取
本文针对电网故障行波网络定位的实际应用,采用Dijkstra算法计算两个节点之间的最短路径,建立最短路径距离矩阵L。
1)假设电网拓扑结构图中共有n个节点,选取线路长度作为权值,构造赋权矩阵V为:
(6)
(7)
式中:lij为相连节点i与节点j之间的线路长度。
2)依据赋权矩阵V中线路长度,采用Dijkstra算法求取电网中任意两个节点之间的最短路径,用Lij表示节点i与节点j之间最短路径所途经线路长度总和,得到最短路径距离矩阵L。
(8)
2.3 最短路径距离元素的修正
最短路径距离矩阵L中有很多路径不经过故障线路,而双端行波定位法必须采用故障线路或经过故障线路的最短路径,所以必须修正最短路径距离矩阵L的部分元素,使得修正后的最短路径包含故障线路。定义修正后的最短路径距离矩阵为计算矩阵L′,修正方法如下。
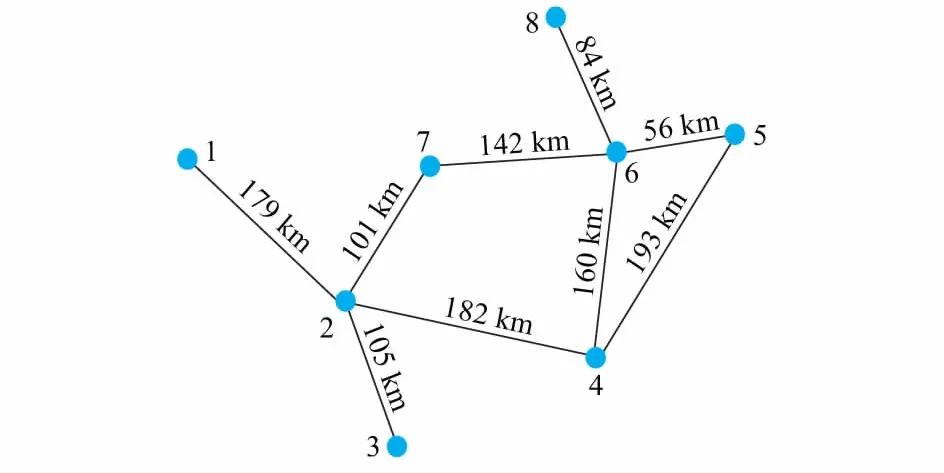
1)考虑到最短路径距离矩阵L为对称阵,且各最短路径为无向路径(即Lij=Lji),所以为避免重复计算,当i 2)当故障线路不在环网中时,将所有不经过故障线路的最短路径元素Lij修正为0,其他元素无需修正。 3)当故障线路位于环网时,为了避免解网运算和充分利用环网中节点的有效数据,根据最短路径的节点位置进行分类讨论,将原本未经过故障线路的最短路径从环网中去除后再次利用Dijkstra算法求取包含故障线路的最短路径。按下列步骤进行修正。 步骤1:如果最短路径元素Lij的两个节点i和j均不在故障线路所在的环网中,当最短路径没有线路在环网中时,将该元素修正为0;当最短路径有线路在环网中时,判别最短路径包含故障线路与否,包含时无需修正,否则将该最短路径从环网中的线路处断开,转步骤4。 步骤2:如果最短路径元素Lij的两个节点i和j均在故障线路所在的环网中,判断最短路径是否包含故障线路,包含时无需修正,不包含时,若节点i和j有一个是故障线路端节点时,由于重新搜索的包含故障线路的最短路径线路偏长,考虑到行波信号衰减,在环网结构比较复杂时,计算的故障误差较大,在其他有效数据量充足的前提下,将这种情况下最短路径元素Lij修正为0;否则将该最短路径从环网中的线路处去除,转步骤4。 步骤3:如果最短路径元素Lij的两个节点i和j有一个在故障线路所在的环网中,当最短路径没有线路在环网中时,将该元素修正为0;当该最短路径与相应初始行波到达时间配对进行计算,故障距离为近似为0或近似等于该最短路径长度时,由双端定位公式原理,说明最短路径不包含故障线路,将该元素修正为0;否则将该最短路径从环网中的线路处去除,转步骤4。 步骤4:采用Dijkstra算法重新求取该两节点间的最短路径,直到最短路径包含故障线路的最短路径为止,计算结束后将包含故障线路的最短路径作为该元素Lij的值。 4)所有元素修正完毕后,得到计算矩阵L′。 采用EMTP仿真软件对某典型500 kV电网进行仿真分析,仿真模型如图1所示。由于行波传播受到过渡电阻、阻波器、线路参数、母线接线方式、容性设备等因素影响,EMTP仿真模型的线路都采取计及频变影响的分布参数模型(J.Marti模型)。 图1 典型500 kV电网结构图Fig.1 Typical structure of 500 kV power grid 假定单相接地故障发生在线路4至线路6离第4变电站30 km处,产生的故障初始行波传播至整个电网,各检测点检测的初始行波信号到达时间如表1所示。 表1 初始行波到达时间Table 1 Arrival time of initial traveling 把断路器状态及初始行波到达时间信号通过定位装置发送到故障定位主站,由故障定位主站通过传来的断路器状态信息判别故障所在线路后再计算故障发生精确位置。具体计算过程如下。 1)建立时间矩阵T为: T=[t1t2…t8] (9) 上式中矩阵元素ti的值分别对应表1中初始行波到达第i个变电站的时间。 2)根据线路长度构造赋权矩阵V。 3)采用Dijkstra算法求取任意两节点之间最短路径,用Lij表示节点i与节点j的最短路径所途经线路的长度和,得到最短路径距离矩阵L为: (10) 4)修正最短路径矩阵L,得到计算矩阵L′为: (11) 5)逐次把计算矩阵L′中的最短路径与时间矩阵T中相对应的时间代入双端定位公式求取故障距离,行波传输速度取2.96×108m/s,并以第4变电站为参考节点,将所有故障距离折算到参考节点,得到故障距离矩阵D为: (12) 6)按2.1节中的判别方法对故障距离矩阵D中所有折算故障距离dij′进行有效性识别,判别结果表明故障距离矩阵D中所有dij′均有效。 7)对故障距离矩阵D中所有有效元素设置权重,得到权重矩阵W为: (13) 8)综合故障距离矩阵D′和权重矩阵W,求得精确故障距离,即 (14) 电网故障定位的故障距离为30.020 km,该故障距离误差较小,且比仅利用故障线路两端初始行波到达时间计算出的故障距离(29.969 km)误差要小,这说明故障定位的准确度能得到较好提高。 由于行波瞬间易逝,受检测技术限制,如果故障线路端变电站检测到的初始行波到达时间有较大误差或没有检测到行波信号,此时用传统故障定位方法会出现较大误差或无法进行故障定位计算,但网络定位法仍能准确计算出故障距离。 3.2.1故障线路一端的行波到达时间有较大误差 假定变电站4记录的初始行波到达时间误差较大,t4=1.2×103μs,其他初始行波到达时间不变。此时利用双端定位方法计算出的故障距离为192.567 km。此时按照本文方法进行故障距离计算,第1步到第4步与3.1节相同,计算过程如下。 1)计算故障距离矩阵D为: (15) 2)对故障距离矩阵D中所有折算故障距离dij′进行有效性识别,按2.1节中的判别方法对故障距离矩阵D中所有折算故障距离dij′进行有效性识别,判别结果表明故障距离矩阵D中第4列所有折算故障距离dij′均无效,其余折算故障距离dij′均有效。故障距离矩阵D修正为: (16) 3)对故障距离矩阵D中所有有效元素设置权重,得到权重矩阵W: (17) 4)综合故障距离矩阵D′和权重矩阵W,求取精确故障距离为: (18) 3.2.2故障线路一端没有检测到行波 假定变电站6没有记录到行波信号,此时t6=0,其他初始行波到达时间不变。此时利用双端定位方法无法计算故障距离,但按照本文故障定位方法仍可进行故障距离计算,第1步到第4步与3.1节相同,后面计算过程如下。 1)计算故障距离矩阵D为: (19) 2)对故障距离矩阵D中所有折算故障距离dij′进行有效性识别,按2.1节中的判别方法对故障距离矩阵D中所有折算故障距离dij′进行有效性识别,判别结果表明故障距离矩阵D中所有折算故障距离dij′均有效。 3)对故障距离矩阵D中所有有效元素设置权重,得到权重矩阵W为: (20) 4)综合故障距离矩阵D′和权重矩阵W,求取精确故障距离为: (21) 传统网络定位方法一般采用Floyd算法搜索网络各节点的最短路径,结合双端定位公式来实现定位。需要进行复杂环网解网运算化为辐射型网,而Floyd算法仅适用于故障线路不在环网的情况。当故障线路在环网时,会出现数据漏算和误算。以本文仿真情况为例,以变电站2和6作为计算点时,实际有效最短路径应为l246,而Floyd算法搜索的最短路径是l276,未经过故障线路,出现漏算。以变电站2和5作为计算点时,实际有效最短路径为l2465,而Floyd算法搜索得到结果是l245,简化网络时极端状态是剔除了故障线路,导致解网失败的情况。 文献[17]提出改进,在保留故障线路的前提下利用Floyd算法寻找最短路径,删除未经过故障线路的最短路径,如图2所示。 图2 强制保留故障线路的解网结果Fig.2 Result of simplified network when reserving fault line 在上述极端情况下的解网直接删除了变电站7和5,减少了有效数据的利用,本文无需解网,同时能计算出环网各个变电站之间的有效最短路径。 综合上述计算结果可知,利用全网行波数据进行故障定位计算可靠性较高,可以在故障线路端数据错误或其他检测点数据错误时仍进行可靠的故障定位计算;且计算过程简单,无须进行复杂环网的解网运算,有效避免了解网错误带来了故障定位误差。 本文提出了一种基于Dijkstra算法的电网故障行波定位新方法。该方法利用Dijkstra算法搜索最短路径,无须进行复杂环网的解网运算,可避免复杂环网在解网运算错误时的故障定位失效或定位误差大问题,能较好提升网络定位的准确度和可靠性;同时该算法通过对故障距离的有效性识别与修正,可在行波数据漏采和误采的情况下,仍能实现准确故障定位。由于Dijkstra算法实行简单,工程应用成熟,本文方法有望在电网中得到更多应用,如在环网结构比较复杂时,结合Dijkstra算法实现环网在保证定位精度的前提下减少定位装置的数量,节约投资成本。3 仿真验证
3.1 所有时间数据均有效时的故障定位计算
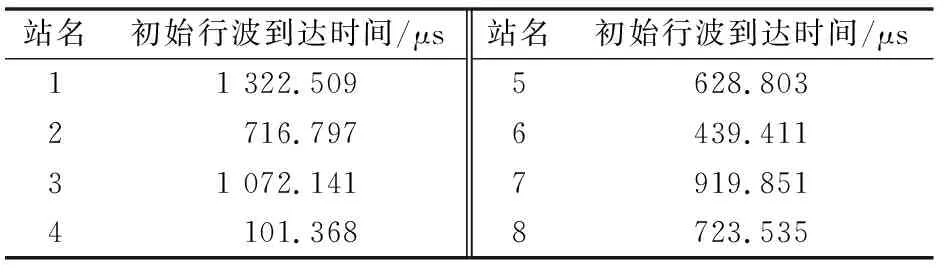
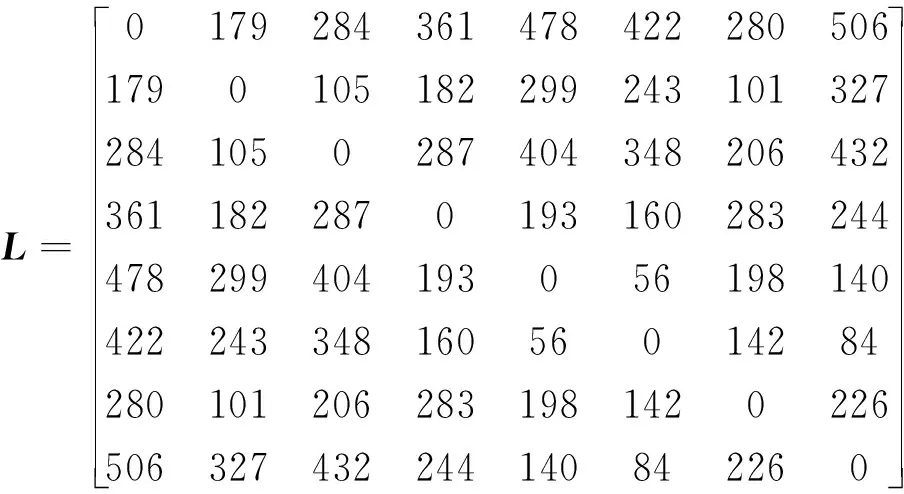
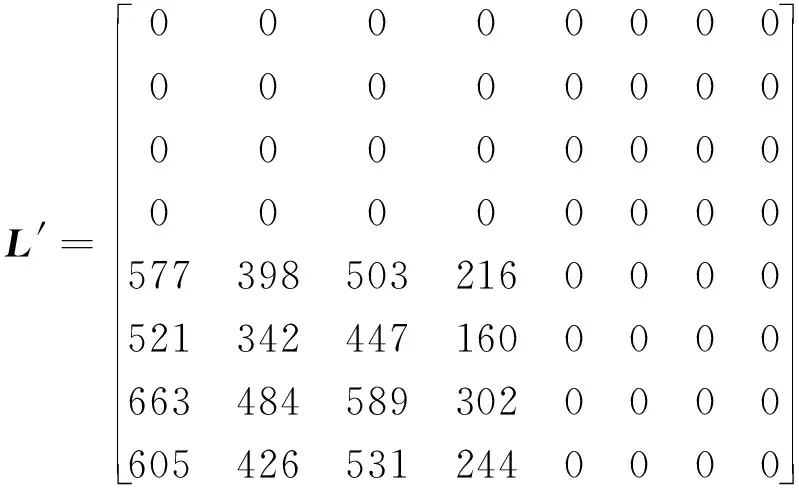

3.2 有无效时间数据时的故障定位计算



3.3 与其他故障行波网络故障定位方法的比较

4 结语

