双馈风电机组中频谐波电流建模与分析

李 庆， 程 鹏， 王伟胜

(新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司)， 北京市 100192)

0 引言

近年来，随着电力电子技术的持续发展和风电装备水平的不断提升，风电已成为中国第三大电源。双馈风电机组(DFIG)由于其功率独立解耦可调、变流器功率容量小等优势而成为主流机型，占据国内70%～80%的风电装机比例。大量双馈风电机组接入电网引起的谐波问题是风电机组脱网和风电场设备损坏的主要原因[1-3]。为准确反映双馈风电机组并网谐波电流特性，并为风电场谐波评估提供手段，建立可评估双馈风电机组定子侧输出中频谐波电流的等效谐波模型很有必要。

根据现有研究结果，可将风电机组输出谐波电流按照频率划分为低于100 Hz的低频段、100～1 000 Hz的中频段和高于1 000 Hz的高频段。

当接入含有串联电容器补偿的网络后，双馈风电机组极易输出低频谐波电流。文献[4]指出，低频谐波电流的产生主要是由于变流器控制系统与电网相互作用，但并未研究控制系统中锁相环对双馈风电机组谐波电流的影响。文献[5-6]采用谐波线性化理论建立了锁相环与电流环耦合的序阻抗模型，并指出锁相环会导致变流器序阻抗呈现负阻特性，从物理概念上明确了谐波电流产生的过程。以此为基础，文献[7-8]则重点研究锁相环带宽对变流器输出低频谐波电流的影响，并提出以降低谐波电流为目标的主动阻尼控制策略。

当双馈风电机组接入含有并联电容器补偿的网络后，易输出高频谐波电流。与低频电流产生机理不同，锁相环的带宽在10～20 Hz范围内，不会对高频谐波电流输出造成明显影响，双馈风电机组输出高频谐波电流主要是自身阻抗与电网阻抗相互作用的结果[9]。为抑制高频谐波电流的产生，文献[9-10]提出引入虚拟阻抗的阻尼提升方案，解决了高频段谐波阻尼不足的问题。

在针对100～1 000 Hz中频谐波电流的研究方面，文献[11]建立了在谐波电压环境下双馈风电机组机侧和网侧变流器的数学模型，评估了背景谐波对其转矩、功率及直流电压的负面影响，并提出了多比例—积分(PI)控制器、多频谐振控制器等方案的双馈风电机组输出电流正弦化控制策略。这些方法着重从双馈风电机组控制方案方面进行技术改进，缺少对其输出谐波电流的分析评估。文献[12-13]研究了对称与不对称电压跌落发生后双馈风电机组的运行行为，建立了用于描述双馈风电机组输出电流特性的数学模型，但并未对谐波电网下的谐波电流成分及其特征进行进一步分析。文献[14]将脉宽调制(PWM)调制死区引入单相逆变器谐波建模与分析中，建立了更加逼近实际并网系统的逆变器模型，但这些分析方法不适用于分析包含旋转电机的并网发电单元谐波特性，还有待进一步深入研究。

因此，本文在介绍双馈风电机组典型矢量控制的基础上，从评估双馈风电机组输出中频谐波电流角度出发，研究了电网背景谐波、PWM调制死区对双馈风电机组定子侧中频谐波电流的影响机理，建立了包含电网背景谐波、PWM调制死区在内,并可评估双馈风电机组定子侧中频电流的数学模型，深入分析了不同影响因素对双馈风电机组输出中频谐波电流的影响规律。最后，通过3.0 MW双馈风电机组仿真研究，验证了所建立谐波模型在评估双馈风电机组定子侧中频谐波电流方面的准确性。

1 双馈风电机组中频谐波电流影响因素

双馈风电机组中机侧变流器(rotor-side converter，RSC)通过对电机励磁电流的调控，实现对定子侧电流和功率的控制，详见附录A图A1。其中，RSC控制系统由电压同步信号检测、功率—电流跟踪控制、PWM三个主要部分构成。

锁相环因其结构简单、实现便捷而成为电网同步信号检测环节的主流结构，实现电压相位和频率的检测，并为控制系统提供坐标基准。两相同步旋转坐标系中，锁相环控制带宽多在10～20 Hz之间[8]，经两相同步旋转坐标到两相静止坐标系的坐标变换，锁相环只会影响30～70 Hz内电流，故可忽略其对双馈风电机组输出中频谐波电流的影响。

功率—电流跟踪控制环节包含功率闭环、电流闭环两个控制环节，实现功率和电流的无静差跟踪[15]。因功率外环的控制带宽多在100 Hz以下，后续研究中可忽略功率外环对中频谐波电流的影响，并且近似认为功率外环输出量不受谐波电压影响而为恒定值。然而，RSC电流闭环的控制带宽处于中频段范围内，将会与电网背景谐波产生相互作用，这是双馈风电机组输出中频谐波电流的影响因素。

PWM环节的主要功能是根据电压调制波获取控制功率器件导通与关断的开关信号，主要有正弦PWM、空间矢量PWM[16]。由于PWM开关频率多在1.5～2.5 kHz之间，则可忽略成组分布在开关频率及其倍频处开关谐波。此外，死区时间的加入将会导致基波电压损失、谐波畸变等现象，是双馈风电机组定子侧输出中频谐波电流的另一个原因。

RSC控制系统中电流闭环与电网背景谐波相互作用及死区时间所产生的实际调制电压与理想调制电压的偏差是谐波电流产生的主要原因。因此，本文在忽略锁相环、功率闭环及PWM开关动作的前提下，建立只考虑电流控制闭环与调制死区时间的双馈风电机组定子侧中频谐波电流的数学模型。

2 双馈风电机组中频谐波电流数学模型

双馈风电机组定子绕组与电网直接相连接，转子绕组经过碳刷和滑环后与RSC相连接，详见附录A图A2。双馈感应发电机相当于接入由外部电源和机侧变流器组成的双电源供电网络。因此，需将双馈风电机组转子绕组与RSC的阻抗折算到定子侧，并根据戴维南定理建立电压源和阻抗相串联的网络，以评估双馈风电机组定子侧谐波电流。

2.1 机侧变流器

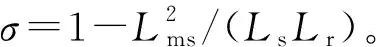
一般机侧变流器采用在两相同步旋转坐标系中的电流PI闭环控制结构，详见附录A图A3，其中，Gc(s)表示电流闭环PI调节器的传递函数，Gd(s)表示由于采样、PWM调制等造成时延的传递函数，Gp(s)表示双馈感应发电机的传递函数，则有

(1)

Gd(s)=e-sTd

(2)

(3)

式中：kp和ki分别为PI调节器的比例系数和积分系数；Td=1.5Ts表示控制系统延迟时间，Ts为控制系统采样时间；Rr为转子绕组的电阻。

在两相同步旋转坐标系中，RSC输出电压指令与转子电流之间的关系，可表示为

(4)

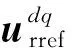
式(5)和式(6)分别给出任意两相坐标系到两相旋转坐标系间的坐标变换Tαβ/dq及其逆变换，则有

(5)

(6)

式中：θ为两相旋转坐标系d轴与任意两相坐标系α轴之间的电角度。

根据式(5)和式(6)，将式(4)给出的两相同步旋转坐标系中转子电压变换到两相转子静止坐标系中，则有

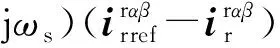
(7)

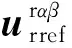
(8)

其中

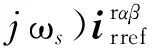
(9)

(10)

图1 机侧变流器与转子绕组等效电路Fig.1 Equivalent circuit of RSC and rotor winding

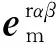
(11)

式(11)在两相转子静止坐标系中给出了双馈风电机组感应电动势，其频率为转差频率。值得注意的是，两相转子静止坐标系是相对转子绕组保持静止，而相对定子绕组以转子角速度旋转，但两相定子静止坐标系则是相对定子绕组保持静止。因此，为计算双馈风电机组定子侧谐波电流，需将式(11)给出的感应电动势变换到相对定子绕组保持静止的两相定子静止坐标系中。由于双馈感应发电机以及电网侧不存在零序三次谐波，则只需考虑正序(6k+1)次谐波和负序(6k-1)次谐波，其中，定子侧(6k-1)次负序谐波电压在转子侧对应的谐波电压角频率为(6k-1)ω1+ωr，而定子侧(6k+1)次正序谐波电压在转子侧对应的谐波电压角频率为(6k+1)ω1-ωr，则定子绕组不同频率电压对应转差率可写为：

(12)

式中：ωh为双馈风电机组定子侧谐波电压角频率，其中h为谐波次数。

根据文献[7-8]，在两相定子静止坐标系中，双馈风电机组定子侧的感应电动势可表示为：

(13)

其中s=jωh=jhω1,且

(14)

(15)

(16)

这里需要指出，由于三相定子静止坐标系与两相定子静止坐标系间所涉及的坐标变换仅为常系数变换，而不涉及电压相位角、转子相位角等周期变化信号。因此，忽略三相定子静止坐标系与两相定子静止坐标系之间的恒系数坐标变换，不会对双馈风电机组定子侧中频谐波电流分析造成影响，但可简化其定子侧谐波电流建模的复杂度。

因此，图2(a)给出了在两相定子静止坐标系中双馈风电机组定子侧等效电路。同时，由于励磁电感远大于定、转子漏感[9]，在分析定子侧中频谐波电流时，可忽略励磁电感，简化后的双馈风电机组等效电路见图2(b)。

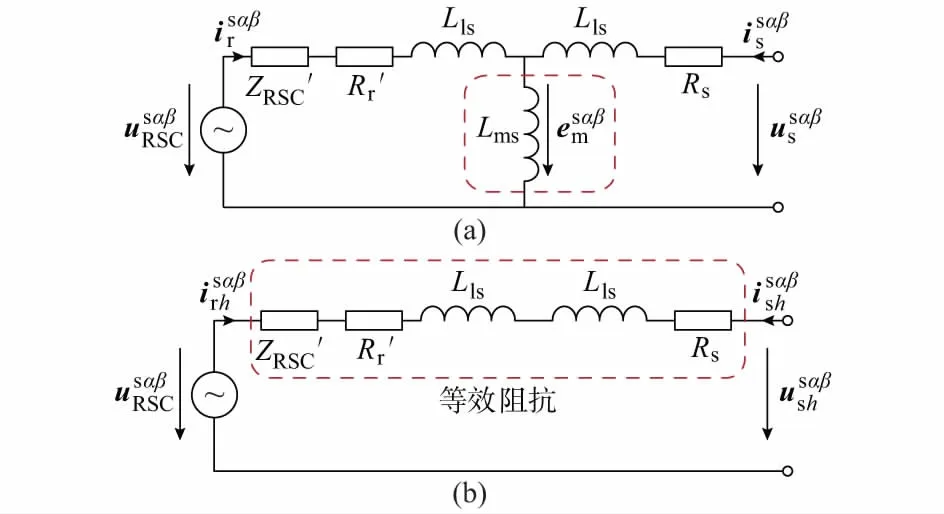
图2 考虑电网背景谐波的定子侧等效电路Fig.2 Equivalent circuit of stator side considering grid background harmonics

根据图2(b)，双馈风电机组定子侧阻抗由机侧变流器等效电阻、转子电阻与漏感、定子电阻与漏感5个部分构成，并可写为

ZD(s)=ZRSC′(s)+Rr′(s)+Rs+s(Llr+Lls)

(17)

因此，双馈风电机组定子侧h次谐波电流与相应频率谐波电压间的关系可表示为：

(18)

根据式(17)和式(18)可知，电网背景谐波引起的谐波电流由外部谐波电压决定，其频率与外部背景谐波电压频率相同并与转速无关，其幅值与RSC控制系统控制策略、双馈感应发电机参数以及转速有关，并且随外部谐波电压的增加而增加。

2.2 死区效应

为了避免同一桥臂上下两个功率器件出现直通现象，须在PWM调制环节中设置死区时间，这将导致实际输出电压与电压指令存在偏差而出现谐波电压和电流，需建立包含PWM调制死区的双馈风电机组中频谐波电流数学模型。

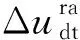
(19)

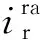
可见，PWM调制死区效应导致的偏差电压表现为方波电压形式，偏差电压正负与转子电流正负相同，幅值由PWM调制死区时间、PWM调制开关频率和直流侧电压共同决定并呈现正相关关系。对式(19)进行傅里叶变换，则有

(20)

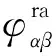
由此可见，RSC输出电压存在丰富的奇数次谐波，并会通过定、转子之间的耦合而传递到定子侧，使其输出电流出现谐波畸变。双馈风电机组转子侧不存在零序三次谐波电流通路，故RSC仅输出(6k±1)次谐波电流。同时，由于谐波电压幅值与谐波次数的反比关系，则其幅值将随着谐波次数的增加而减少，因此本文只研究低于20次转子谐波电流。

此外，PWM调制死区效应产生的谐波电压存在正、负序差异，将导致不同频率谐波对应的转差率不同，则在分析双馈风电机组定子侧谐波电流时，需根据各次谐波对应的转差率进行折算。根据式(12)可知，(6k-1)次的负序谐波电压变换到定子侧后，其角频率将变为(6k-1)ωs-ωr，而(6k+1)次的正序谐波电压在折算后，其角频率将变为(6k+1)ωs+ωr。附录A表A1、表A2和表A3分别给出了在800，900，1 200 r/min转速下双馈风电机组定转子谐波电流频谱对照表。

根据式(12)和式(20)，折算到定子侧后，PWM调制死区效应引起的定子a相谐波电压可表示为：

(21)

式中：ωdt为折算到定子侧后调制死区产生谐波电压的频率,具体有

(22)

(23)

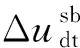
(24)

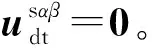
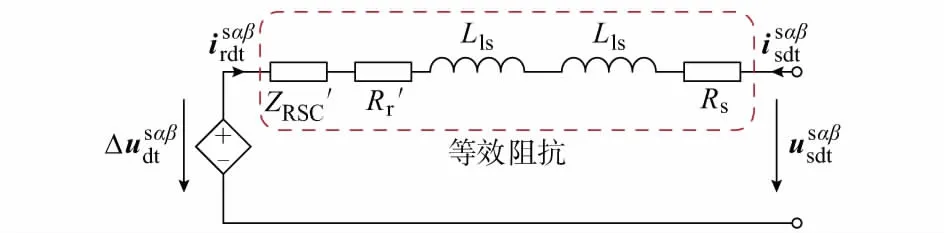
图3 考虑死区效应的定子侧等效电路Fig.3 Equivalent circuit of stator side considering PWM dead time effect

因此，PWM调制死区效应产生的谐波电流可简化表示为：

(25)

PWM调制死区效应产生的谐波电流由死区效应引起的谐波电压决定，并与RSC控制系统控制策略、双馈风电机组参数以及转速相关，其频率在定子绕组中呈现转差频率与转子角频率的和或差，而非工频整数倍，其幅值与死区时间、直流侧电压和开关频率之间呈现正相关，但随着谐波次数增加而降低。

2.3 输出电流

图4给出了考虑电网背景谐波和PWM调制死区效应的双馈风电机组定子侧等效电路，具体有

(26)

图4 考虑背景谐波和死区效应的定子侧等效电路Fig.4 Equivalent circuit of stator side considering grid background harmonics and dead zone effect

可见，双馈风电机组定子侧谐波电流，由RSC输出电压与电网电压差值在内阻抗ZD形成的谐波电流，叠加由调制死区效应产生的独立谐波电流源后形成，具体有

(27)

实际应用中，由于RSC定子功率外环控制带宽较小而可忽略谐波电压对其的影响，并近似认为其输出为恒定量，则式(9)给出的RSC输出电压在两相定子静止坐标系下呈现无谐波的工频正弦量形式。因此，可忽略RSC机侧变流器输出电压对定子侧谐波电流的影响，则式(27)可简化为

(28)

因此，双馈风电机组定子侧中频电流表现为两种典型频率：①与双馈风电机组转速无关且与电网背景电压谐波频率相同的整数次谐波电流，这部分典型谐波电流是由于电网背景电压存在谐波所产生，并且从定子侧注入，在定子绕组中呈现工频的(6k±1)倍；②与电网背景电压谐波频率无关、与转速有关的非整数次谐波电流，这部分谐波电流是由RSC调制死区效应所产生的，并且从转子侧流向定子侧，在转子绕组中呈现转差角频率的(6k±1)倍。

3 仿真研究与实测验证

为了验证前文理论分析的正确性，本节首先在MATLAB/Simulink仿真软件上，建立了3.0 MW双馈风电机组仿真模型，通过仿真结果与计算结果的对比说明公式计算的准确性。附录B表B1给出了双馈风电机组网侧变流器的主要参数。而后，通过与3.0 MW双馈风电机组现场测试得到的输出谐波电流进行对比分析，进一步说明前文理论分析与推导公式的正确性。

3.1 仿真研究

图5给出了定子侧谐波电流计算值与仿真值对比结果，其中，纵坐标为各次谐波占额定功率下基频电流幅值的百分比，横坐标为相应的谐波电流频率。

在仿真研究中，电机转速为800 r/min，定子侧输出20%额定功率(0.6 MW)，调制死区时间为15 μs，假定电网电压含有5，7，11，13，17，19次谐波，其幅值分别为14.0，8.0，5.0，2.0，1.0，0.5 V，则电网电压谐波畸变率(THD)为3.03%。针对由电网背景谐波所引起的定子侧5次250 Hz谐波电流，通过仿真模型获取的谐波幅值为63.4 A，而通过数学模型计算获取的谐波幅值为63.1 A。针对由调制死区所引起的转子侧7次谐波电流在定子侧呈现110 Hz谐波电流，通过仿真模型获取其幅值为15.65 A，而通过数学模型计算获取的电流幅值为16.59 A。附录B表B2给出了其余频率处谐波电流的仿真值和计算值，二者保持了良好的一致性，从而也验证了前文理论分析和推导公式的正确性。

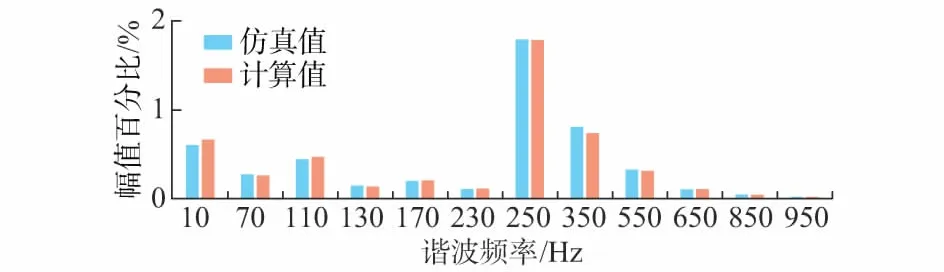
图5 定子侧谐波电流仿真值与计算值对比Fig.5 Comparison of simulated and calculated values of harmonic currents at stator side

附录B图B1至图B5分别给出不同电网背景谐波幅值、不同调制死区时间、不同电流环控制带宽、不同电机转速和不同有功功率下，双馈风电机组定子侧谐波电流仿真与计算对比结果，具体数值详见表B2至表B6。可见，定子侧谐波电流仿真与计算结果均保持较好的一致性，并说明：由电网背景谐波所引起的定子侧整数次谐波电流频率与背景谐波频率相同，而其幅值正比于相应谐波电压幅值且受电机转速、电流控制带宽的影响；由调制死区引起的定子侧非整数次谐波电流频率与电机转速有关，而其幅值正比于调制死区时间，并且与电机转速、电流控制带宽有关。

3.2 实测验证

附录B图B6给出了某3.0 MW双馈风电机组现场测试示意图，其中A点为电压测量点，B点为定子电流测量点。在现场测试中，采用DEWETRON公司生产的DEWE-3020型数据采集系统，采集风电机组的机端电压，并采用法国C.A公司生产的P01120054A型电流互感器采集定子侧输出电流，详见附录B图B7。图6给出了某型号双馈风电机组定子侧谐波电流的实测数据与计算结果的对比图，具体数据详见附录B表B7。

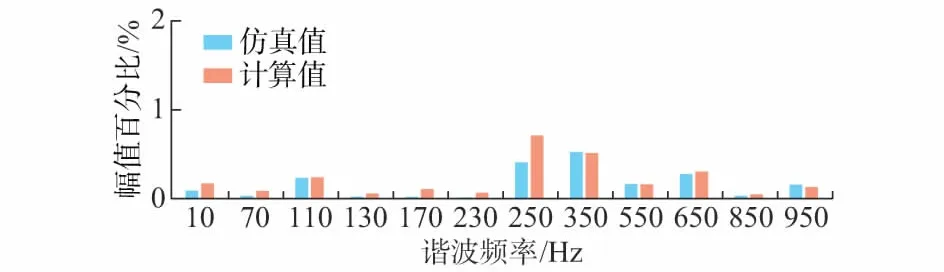
图6 定子侧谐波电流实测值与计算值对比Fig.6 Comparison of measured and calculated values of harmonic currents at stator side

在现场测试中，风电机组运行于额定功率状态，电网电压含有0.91%的5次谐波、0.45%的7次谐波、0.19%的11次谐波、0.43%的13次谐波、0.08%的17次谐波和0.26%的19次谐波。可见，定子侧谐波电流的仿真计算结果与实测结果保持了良好的一致性，但在5次谐波处偏差相对较大，这主要是由于由风电场内其他风电机组谐波发射作用，致使测试点5次谐波与其他谐波源5次谐波发生抵消。

总之，该数学模型能够准确模拟谐波电网环境下双馈风电机组定子侧谐波电流频率和幅值，并可有效评估电网环境、控制参数与运行工况对定子侧谐波电流的影响。

4 结语

本文建立了双馈风电机组定子侧中频谐波电流的数学模型，综合分析了双馈风电机组定子侧中频谐波电流的影响因素，并开展了仿真研究与实测对比分析，得到以下结论。

1)双馈风电机组定子侧整数次谐波电流由电网背景谐波电压所引起，其频率与背景谐波电压频率相同，其幅值正相关于背景谐波电压幅值，并受到电流环控制带宽的影响，但与有功功率、电机转速基本无关。

2)双馈风电机组定子侧非整数次谐波电流由调制死区所引起，其频率与电机转速有关，其幅值正相关于调制死区时间，并受到电流环控制带宽的影响，但与定子侧有功功率基本无关。

通过仿真、计算和实测结果对比验证了该数学模型的准确性和有效性，模型可为风电机组和风电场谐波评估与治理提供方法和依据。在后续研究中，还需研究网侧变流器的谐波电流特性，建立并网点处双馈风电机组输出谐波电流的数学模型。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。