紫外--可见光谱法水质监测中浊度影响的非线性校正*

方坷昊， 赵 凌

(四川师范大学 数学与软件科学学院，四川 成都 610068)

0 引 言

目前紫外—可见光谱法在水质检测中已经取得较为成熟的研究成果，国外学者[1]首次提出了紫外—可见光谱法，选取波长为254 nm处的吸光度应用最小二乘法对水体化学需氧量(chemical oxygen demand，COD)值建立回归模型,取得了较为精确的结果，一些学者[2]提出对于复杂水体，波长为254 nm处吸光度的大小受到多种物质影响，当存在多种污染物时，模型精度受到较大影响，并提出选取633 nm处波长吸光度对254 nm处进行补偿；何金成[3]应用偏最小二乘法选取多个波长吸光度作为因变量建立回归模型，但由于浊度对COD特征波长所在的紫外波段的影响是非线性的，模型效果并未得到本质性的提高。一些学者[4,5]通过光学散射原理的研究对全波段进行补偿，获得了较好的精度，但由于其方法需要先验得到浊度颗粒的折射率，其测量获取难度远高于直接对水体COD的测量，导致模型难以应用于对未知水体的监测。

为解决上述问题，本文改进了浊度对COD特征波段254 nm处吸光度的补偿模型。首先配置不同浓度的邻苯二甲酸氢钾和福尔马肼溶液分别作为COD标准液和浊度标准液对紫外—可见光谱的各波段吸光性进行分析，验证浊度对紫外光谱影响的非线性特征；建立非线性的多项式模型对其建立补偿模型，使用高斯—牛顿法对模型的参数估计进行逼近，得到最优模型；通过7组浊度与COD混合液的紫外—可见光谱数据代入模型与实测值进行验证。

1 数据来源与分析

1.1 数据来源

本文基于朗伯比尔定理对不同污染物的稀溶液进行定量分析，COD溶液选取邻苯二甲酸氢钾作为溶质进行配置，其具有性质稳定、能够被完全氧化、可见光段不吸收的特点，在定量控制和定性分析方面均具备较好的操作性。由于样品能溶于水，为了减少实验系统误差，首先在105 ℃条件下对样品烘干2 h，置于干燥环境冷却后，准确称取0.063 6 g,邻苯二甲酸氢钾倒入洁净的500 mL烧杯中，缓慢加入350 mL蒸馏水并不停搅拌，待其完全溶解后滴加0.1 mL浓度为98%的硫酸，用玻璃棒将溶液引流至500 mL的容量瓶中，并用蒸馏水定容，此时溶液的COD值为150 mg/L,最后再分别稀释得到COD值为0～115 mg/L之间、间隔为1 mg/L的116组标准溶液，记为数据组1。

在标准浊度溶液配置中，一般选取福尔马肼为溶质。福尔马肼溶液一般由硫酸肼溶液与六次甲基四胺溶液以1∶10的浓度配置得到。取用5 mL浓度为10 mg/L的硫酸肼溶液与5 mL浓度为100 mg/L溶液加入100 mL容量瓶中，在25 ℃条件下反应24 h后定容至标线，此时配得浊度为400 NTU的浊度标准液，最后分别稀释得到浊度为0～400 NTU之间间隔为10 mg/L的41组标准溶液，记为数据组2。

不失一般性，配置3组浊度与COD溶液的混合液作为验证组，收集4组不同地域的实际河水水样加入验证组对模型进行实证，标记为数据组3。为排除其他因素对实验的影响，在相同温度，压强条件下对所有水样扫描10次，经小波变换平滑去噪后取其均值得到光谱吸光度数据。

1.2 数据分析

对光谱波长吸光度与单因素水体浓度进行定量分析，找出不同污染物对不同波长吸光度的影响特征，基于单因素污染物特征建立复杂水体模型。

选取200 NTU浊度和50 mg/L混合液、浓度为200 NTU的浊度溶液、浓度为50 mg/L的COD溶液及蒸馏水4组水样。其全光谱吸光度数据如图1可知：1)COD溶液与浊度溶液均对特定波长有不同吸光性；2)在其余条件均相同的情况下，COD浓度变化仅对紫外波段的吸光度有影响。可见波段对COD几乎不吸收；3)浊度过高会造成光学散射从而对每个波长的光能量造成损耗，引起光谱的大幅抬升，因此，在光谱水质检测的模型建立过程中，必须对浊度散射影响进行补偿。

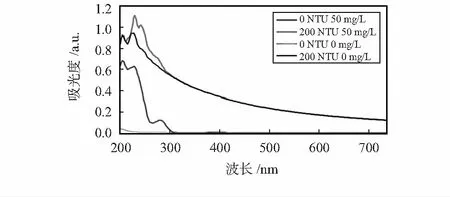
图1 浊度和COD对吸光度的影响对比

1.3 特征波长选取

COD吸收特征波段为240～300 nm，选取254 nm波长作为COD特征波长进行分析；此前，多数学者通过构造633 nm处吸光度与254 nm处吸光度的统计量的方式对进行补偿，但经光谱图数据分析，浊度数据在560 nm处有比633 nm处更好的相关性。因此，选取560 nm波长作为浊度特征波长，分别绘制出数据组1和数据组2中254，560 nm 2个特征波长吸光度的变化如图2，由于2组数据分别只存在一种污染物变量，此时，对应波长处的变化均由该污染物造成。

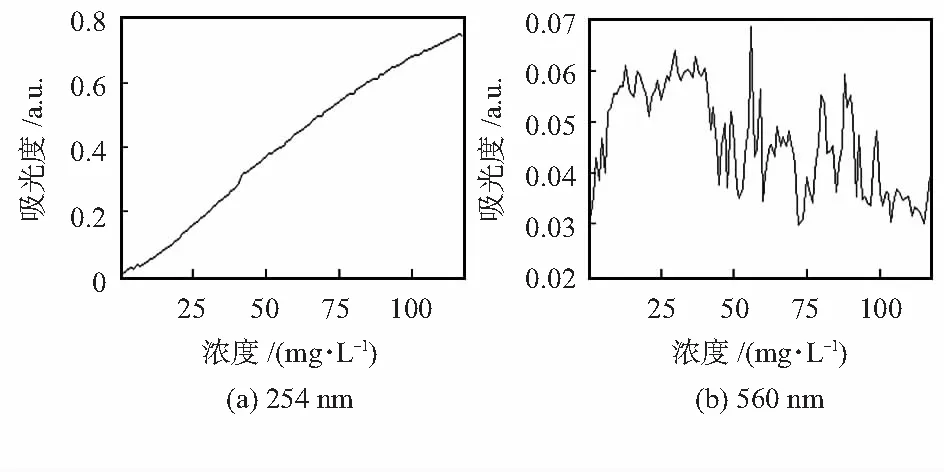
图2 COD在不同波长处的吸光度

2 模型建立与评价

2.1 COD预测模型建立与分析

254，560 nm处吸光度随COD变化如图2所示，随着COD浓度升高，560 nm处吸光度呈无序变化，不存在随浓度增加而增加的趋势，验证了COD在560 nm处不吸收；254 nm处吸光度与COD浓度呈线性的正相关关系。根据COD的光谱吸收特性，将数据组1中的236，242，245，250，254 nm处波长的吸光度作为自变量且记为A236,A242,A245,A250,A254，将COD值作为因变量建立偏最小二乘模型，此时建立的模型为无浊度影响的COD预测模型

COD=-0.438-5.405A236+7.681A242+6.238A245+

11.545A250+9.710A254

(1)

根据交叉有效性原则确定成分数量为2，决定系数为0.984，残差平方和为30.9,标准误为1.73，参数均通过了T检验。说明模型效果较好。

2.2 浊度补偿模型建立与分析

浊度在2个波长处的吸光性如图3。

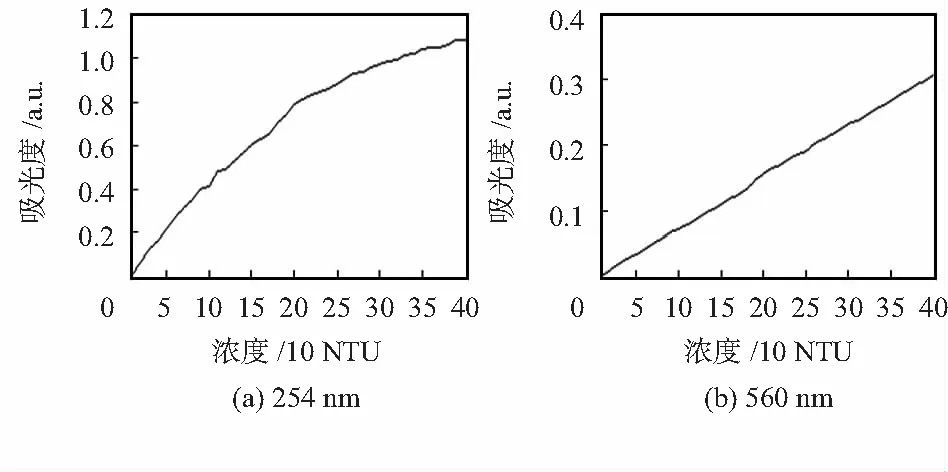
图3 浊度在不同波长处的吸光性

表明随着浊度浓度升高，560 nm处吸光度与浓度呈正相关关系，用最小二乘法拟合得决定系数为0.99，模型参数通过T检验，说明560 nm处吸光度可以作为浊度的特征波长对254 nm进行补偿；254 nm处吸光度与浊度浓度呈正相关关系，且随着浊度浓度的增加，吸光度的变化率减小，表现出非线性特性。因此，浊度对紫外波段造成非线性影响，应建立非线性模型对紫外波段吸光度进行补偿，但由于传统的变量变换法所建立的非线性模型会造成模型因变量均值在变换后产生偏移，且不能够保证模型残差平方和最小，基于此，采用高斯—牛顿法分别用数据组2中236，242，245，250，254 nm处吸光度数据为因变量，560 nm处吸光度为自变量建立非线性模型(式(2))，此时紫外波段的吸光量可看作全部由浊度散射造成

(2)

式中A236c，A242c，A245c，A250c，A254c为对应波长处吸光度补偿值;A560为560 nm处吸光度；ε为随机扰动项。模型参数均通过T检验，拟合精度较好，如表1所示。

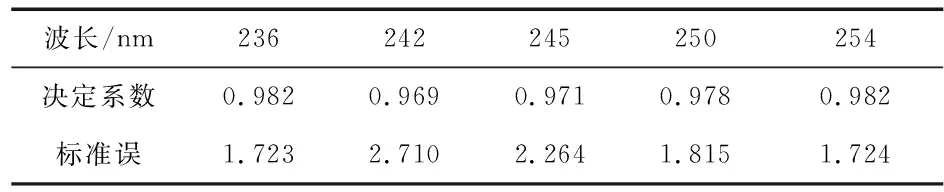
表1 拟合效果表

综上，560 nm处吸光度仅被水体浊度浓度的大小线性影响，紫外波段吸光度同时被水体中浊度浓度非线性影响和COD浓度线性影响。此时应该用非线性模型对COD的特征波长236,242,245,250,254 nm吸光度进行补偿，在原始吸光度数据的基础上减去对应波长的补偿吸光度后的吸光度代入式(1)才能反映真实COD浓度。

3 实验分析

基于以上的模型研究，数据组3选用用福尔马肼溶液及邻苯二甲酸氢钾溶液配置3组不同浓度的混合液进行验证，并采集金马河、四川师范大学校园湖、南充嘉陵江、四川省无线电厂四处不同水源的光谱原始数据加入验证组。用化学方法测得浓度作为水样各污染物的实际浓度。将560 nm波长处吸光度数据代入式(2)，分别求得236，242，245，250，254 nm处波长校正吸光度，对5个波长原始吸光度吸光度与演算得到对应波长的吸光度补偿值作差，得到的结果为校正后的吸光度，代入式(1)可得拟合值(表2)。

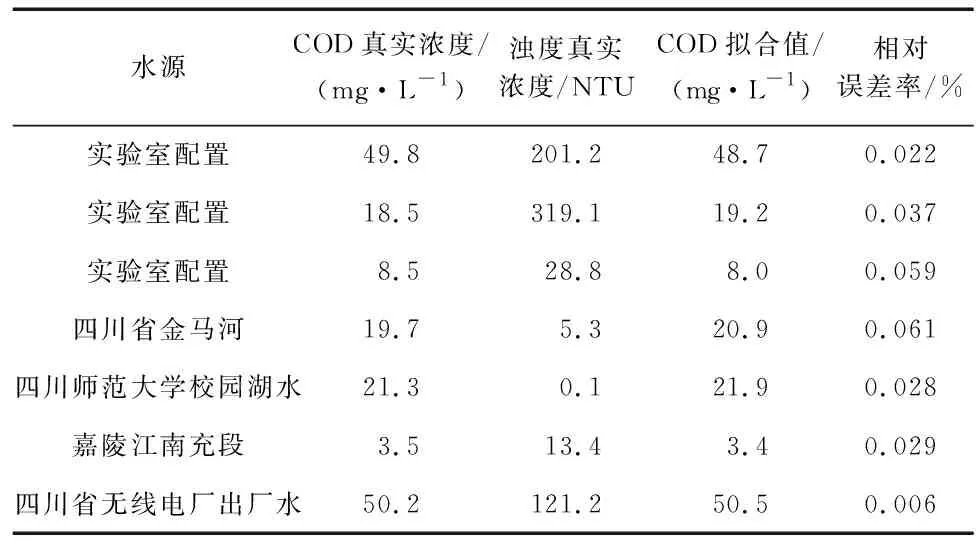
表2 模型拟合值与真实值对比

由表2可知，使用高斯—牛顿法建立的多项式模型最大相对误差率为13.0 %，最小相对误差率为0.6 %,平均相对误差率为3.5 %，非线性模型更适用于紫外—可见光谱中的浊度影响分析。

4 结 论

本文提出的校正方法考虑了浊度对紫外波段吸光度影响的非线性特性及建模步骤中的合理性，选用高斯—牛顿法进行非线性模型建立，由此保证了模型精度；建模过程不需要水质中浊度颗粒类型的先验信息，简化了建模步骤，具有更好的可操作性，说明多项式模型更适用于紫外—可见光谱中的浊度对紫外光谱波段的补偿研究。