加权质心鱼群算法在WSNs节点优化布置中的应用*
何 旭, 彭珍瑞, 董海棠, 殷 红
(兰州交通大学 机电工程学院,甘肃 兰州 730070)
0 引 言
风机叶片是风电机组主要部件[1],叶片工作环境恶劣,检修成本高,因此,考虑减少运行风险,降低维护成本,对叶片进行健康监测具有重大意义[2]。
叶片健康监测主要采用模态测试技术,测试并分析其动力特性。在叶片上安装若干加速度传感器,用以提取模态参数,由于叶片与机舱间存在相对运动,如不使用装置固定,无法使用有线传输;且传感器数目多、布设线缆复杂,需使用无线传感器网络(wireless sensor networks,WSNs)将叶片的状态信号实时传输至接收装置[3]。布置WSNs测点,既增大传输距离,需解决有线传输中的布线问题[4,5],又使系统不易受环境干扰,运行更稳定。
本文将加权质心算法[6](weighted centroid algorithm,WCA)引入人工鱼群算法 (artificial fish swarm algorithm,AFSA) 中初始化鱼群,通过节点之间相互测距和定位补偿误差,并采用自适应变步长,提高了算法的收敛速度和寻优精度。
1 叶片WSNs节点优化布置数学模型
建立叶片有限元模型,提取振型矩阵φn×m,矩阵的行n对应节点自由度数,列m对应模态阶数,从n行中选择s行作为传感器的优化布置测点位置。选择模态置信准则(modal assurance criterion,MAC)[7]最大非对角元素作为传感器优化布置问题的目标函数,数学模型为
(1)
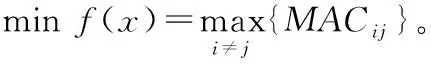
2 加权质心鱼群算法
AFSA[8,9]算法存在问题为:通过随机方式产生初始鱼群,分布不均匀,降低了算法的全局搜索能力,寻优精度有待提高;每条人工鱼的步长是固定值,在迭代前期容易陷入局部最优,收敛速度有待提高。为此引入WCA产生初始鱼群及改进步长的策略,提出了一种用于WSNs节点优化布置的加权质心鱼群算法。
2.1 WCA-AFSA实现流程
2.1.1 二进制编码

二进制编码X与模态矩阵φs×m间的转换为从φn×m删除对应X中{xj|xj=0,j∈[1,2,…,n]}行的过程,即
φs×m=g(φn×m,Xn×1)
(2)
式中 模态矩阵φs×m为布置s只传感器的解;Xn×1为对应于该解的二进制编码。
2.1.2 WCA初始化鱼群
质心算法[6]通过选取距离待定位节点较近的3个交点组成三角形,求其质心,为待定位节点估计位置
(3)

(4)
WCA[11,12]通过合理分配权重,较质心算法定位更精确。令权值与已知节点到未知节点距离的n次方成反比,有
(5)
式中wij为已知节点j对未知节点i的权重值;Pi(x,y)为未知节点i的估计位置;Bj(x,y)为已知节点j的位置;dij为已知节点j到未知节点i的距离估计值;n为权重系数;N为已知节点个数。
在100 m×100 m的区域内随机分布50个WSNs节点,设WSNs节点的无线射程R=50 m。由仿真结果图1知,质心算法误差比WCA误差大,WCA较质心算法定位更精确。

图1 加权质心与质心算法定位误差对比
2.1.3 聚群行为
步长step越大,最大迭代次数Nmax越小,收敛速度越快,但求解精度下降[13]。因此需合理确定参数step,采用一种基于动态参数自适应的变步长策略,即搜索初期步长较大,加快收敛速度;随着迭代次数的增加,逐渐接近最优解,变为小步长进行精细化搜索,提高寻优精度。设计步长为
(6)
式中step为初始步长,visual为人工鱼视野长度。可以看出,Nmax越大,步长非线性减小,甚至达到step/10。步骤如下:
1)计算本次步长nstep。
2)从区间[-nstep,nstep]中随机生成整数Δxij,组成Δxij=[Δxi1,Δxi2,…,Δxin]T。
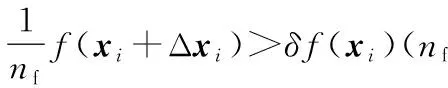
4)重复步骤(1)~步骤(3),直至Nmax为止。
2.1.4 追尾行为
第i条人工鱼追尾过程为:
1)在区间[xij-visual,xij+visual]中,j=1,2,…,n内随机产生人工鱼新位置x'i;

3)重复步骤(1)和步骤(2),直至Nmax为止。
2.1.5 觅食行为
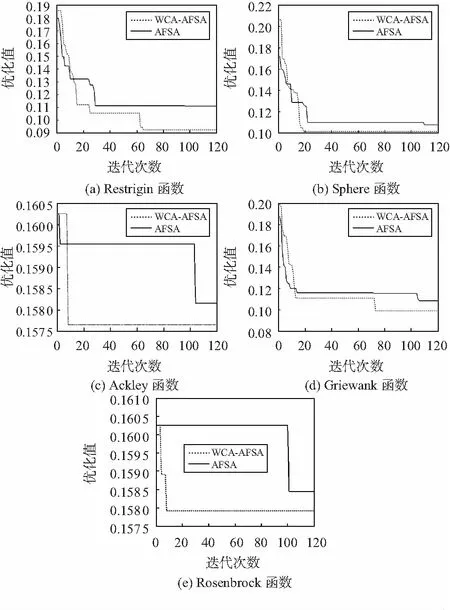
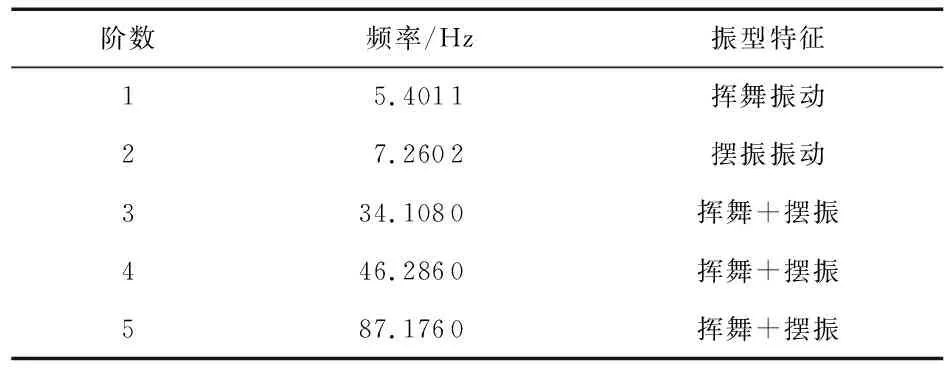
人工鱼当前位置xi,感知范围内的某位置xj,若食物浓度f(xj) 引入自适应变步长技术,寻优初期,距离最优值较远的人工鱼,采用较大步长,快速逼近最优值;接近最优值时,采用较小步长,提高精度[14,15]。 时间复杂度用于衡量算法效率的高低[15,16]。根据WCA-AFSA算法实现步骤分析其时间复杂度: 1)初始化N条人工鱼需N次,时间复杂度为O(N)。 2)初始化参数,比较N-1次,赋值1次,时间复杂度为O(N)。 3)聚群行为计算δ需N次,判断 1次,移动1次,N条人工鱼聚群N次,时间复杂度为O(N2+2×N)。 4)追尾行为搜索最优值N次,计算δ需N次,判断1次,移动1次,N条人工鱼追尾N次,时间复杂度为O(2×N2+2×N)。 5)觅食行为最多try_number次,最少1次,N条人工鱼觅食N次,时间复杂度最多为O(N×try_number)。 算法经l次迭代后,时间复杂度为O(l×3×N2+N×try_number+4×N))。 WCA-AFSA流程如图2所示。 图2 WCA-AFSA流程 分析3个重要参数:设置鱼群规模N=10,初始步长step=0.5,最大迭代次数Nmax=120,取平均值,分析结果如表1所示。 对5个标准函数[14~18]测试,迭代次数120次,取平均值作为求解结果如表1所示。对比曲线如图3所示。 表1 测试函数求解结果 图3 WCA-AFSA与AFSA收敛对比曲线 由表1和图3得出:WCA-AFSA较AFSA提高了收敛精度、加快了收敛速度,WCA-AFSA更为有效。 某兆瓦(MW)级水平轴风机叶片[19],长29 m,玻璃钢材料,密度为1 950 kg/m3,弹性模量为16.5 GPa,泊松比为0.305。各阶频率及振型特征如表2。 表2 叶片前五阶模态频率及振型特征 大型风机叶片的低阶模态具有较大的振型参与系数,能描述结构动态特性。因此选择叶片的前五阶模态作为目标模态[18]。叶片低阶振型以挥舞振动为主,所以研究叶片挥舞方向传感器的优化布置,挥舞方向自由度为主自由度,共1 073个节点自由度,因叶尖处较难布置传感器,将叶尖处36个自由度忽略不计,叶片的前五阶模态矩阵φ为一个1 037×5阶的矩阵。 对风机叶片布置10个WSNs节点进行研究。如图4(a)所示,是经AFSA优化的MAC柱状图;此时MAC最大非对角元素为0.122 655;图4(b)是经WCA-AFSA优化后的MAC柱状图,MAC最大非对角元素为0.008 995。说明改进后算法更为优越。 图4 MAC矩阵柱状图 根据工程实际和试验经验,叶片结构健康监测中多选用加速度传感器[19,20],在风机叶片上布置10个WSNs节点的方案如表3。 表3 加速度传感器布置方案 表3所得传感器布置位置较分散,避免了传感器局部集中导致采集数据不完整的情况;且传感器位于叶片最不利工况位置,即叶根处和翼型变化较大的位置,可以全面获取叶片健康状况信息。 1)引入WCA产生初始鱼群,增加种群多样性,减小计算规模,提高寻优精度; 2)采用一种基于动态参数自适应变步长,迭代前期以较大的步长跳出局部最优解,加快收敛速度,逐渐接近最优解;迭代后期以小步长搜索,能够更精确地寻找到最优解; 3)将WCA作为一种算子引入到AFSA中,充分利用两种成熟算法的优势互补,提高算法的收敛速度和寻优精度。2.2 自适应变步长技术优势分析
2.3 时间复杂度分析
2.4 WCA-AFSA流程

3 WCA-AFSA性能测试及结果分析
3.1 参数设置
3.2 求解结果

4 WCA-AFSA的WSNs节点优化布置
4.1 风机叶片算例

4.2 传感器优化布置方案

5 结 论

