基于集成学习的复杂仿真模型验证方法

周玉臣, 方 可, 马 萍, 杨 明

(哈尔滨工业大学控制与仿真中心, 黑龙江 哈尔滨 150080)

0 引 言

校核、验证与确认(verification, validation and accreditation, VV&A)贯穿于复杂仿真模型开发的全生命周期,模型验证能够确保对模型中缺陷与错误的早期检测,及时解决各设计开发阶段所暴露出的问题,从而保证仿真模型的可信性与正确性,降低应用风险。

复杂仿真模型验证具有评估对象复杂、数据量大、组织实施困难等特点。文献[1]指出为了保证模型在应用域内有效,需要对不同想定下获得的仿真数据与参考数据进行比较,这一过程往往经济成本与时间成本较高。

如何有效利用海量数据对复杂仿真模型进行验证是目前模型验证方法面临的挑战之一。相似性分析是复杂仿真模型验证的主要手段,数据的多样性导致验证过程中需要使用不同的数据相似性分析方法。研究人员提出了大量的相似性分析方法对仿真时间序列与参考时间序列的相似性进行度量,文献[2-4]对数据相似性分析方法进行了综述。不同的相似性分析方法可以度量仿真模型输出与参考系统输出某一个或者某几个方面的相似性程度,而无法全面的分析具有不同特征的时间序列间的相似性。文献[5]提出了一种基于神经网络的周期性时间序列相似性度量方法,该方法通过将数据进行频域转换,利用欧式距离度量时间序列在频域的相似性程度。文献[6]利用随机神经网络(probability neural network, PNN)对定量分析结果与专家主观相似性评定结果的映射关系进行学习。利用机器学习方法设计适用范围更广的相似性分析方法是有效应对海量数据相似性分析问题的主要途径。

文献[7]指出仿真模型验证并不是要判断仿真模型能否完全复现出仿真对象,而是判断仿真模型的输出误差是否大到淹没其有用性。相对于获得仿真模型输出的可信度数值,数据的相似性程度或者指标的可信度等级对于可接受分析同样是有效的。

本文将复杂仿真模型验证中的数据相似性分析转化为可信度等级分类问题,实现大量数据的快速分析。区别于现有文献采用单一类型的分类器模型完成多分类任务,本文尝试将多个不同类型或者不同结构参数的分类器进行集成,从而提高集成分类系统的准确率与泛化能力。

1 问题描述

首先阐述了复杂仿真模型验证要素,之后将模型验证指标的可信度计算转化为多分类问题。

定义1仿真模型验证可以用四元组描述：

CΩ={K,D,A,M}

(1)

式中,K,D,A,M分别表示仿真模型验证指标体系、验证数据集、可接受准则集、相似性分析方法集。

仿真模型验证指标体系描述了影响仿真模型可信度的所有因素,典型的评估指标体系构建方法包括基于层次分析法的树形评估模型构建方法、基于多属性决策网(multiple attribute decision network, MADN)的网状评估模型构建方法等。

定义2[8]基于MADN的仿真模型验证指标体系可以表示为：K={〈N,V〉;〈B,W〉;C;T},式中,N,V,B,W,C,T分别表示节点集、取值集、有向边集、权重集、条件集和阈值集。

定义3D={〈S1,O1,Nλ1〉;〈S2,O2,Nλ2〉;…}为验证数据集。其中,Sk与Ok分别表示模型验证指标Nλk在相同想定下的仿真数据与参考数据。

定义4A={〈N1,A1〉;〈N2,A2〉;…}为可接受准则集。其中,Ak表示第k个验证指标Nk对应的可接受准则。可接受准则与模型验证指标体系中的指标一一对应。

定义5M={〈M1,G1〉;〈M2,G2〉;…}为相似性分析方法集。其中,Gk表示第k种相似性分析方法Mk的适用范围。相似性分析方法包括主观分析方法、静态统计学分析方法、时间序列分析方法等。

仿真模型验证过程中单个指标的评估过程如图1所示,对于模型验证指标Nk,选择对应的仿真数据与参考数据;之后,在分析方法集Mk中选择合适的数据相似性分析方法对仿真数据与参考数据的相似性进行分析,获得Nk的可信度Vk;最后对其进行可接受性分析,获得该指标通过或者不通过可信度评估的结论。

图1 单个指标的模型验证过程Fig.1 Model validation process of single factor

复杂仿真模型验证一方面可以获取模型整体的可信度结果,另一方面可以定位可信度缺陷的节点,以支持仿真模型的改进。显然,仿真模型越复杂,需要评估的指标越多。传统的仿真模型验证工作模式中,由分析人员对每个指标配置数据及相似性分析方法,其效率较低;不适用于利用大量数据对各个验证指标进行分析。引入机器学习相关成果可以显著提高模型验证的效率,实现对大数据集的快速分析。

仿真模型验证是分析模型精度是否能够在其应用域内代表真实物理系统的过程,而不是决定模型正确与错误。对于仿真模型,并不要求其众多输出完全匹配真实系统输出。在一定程度上,相对于连续的可信度值,可信度等级足够用于判定模型的输出是否有效。将模型验证指标的可信度等级作为仿真时间序列与参考时间序列相似性分析结果,则模型验证问题可以作如下描述：

对于模型验证指标Ni,仿真时间序列记为Si=[(ti,1,si,1),(ti,2,si,2),…],参考时间序列记为Oi=[(ti,1,oi,1),(ti,2,oi,2),…];oi,k与si,k为时刻ti,k验证指标的输出值,可信度等级表示为{C1,C2,…,CΛ}。利用不同的准则提取Si与Oi的相似性特征,进而利用样本数据构建分类模型,预测Ni的可信度等级。可信度等级可以采用离散数值描述,如{Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ},或者采用语义描述,如{完全可信,非常可信,可信,一般可信,不可信}。

2 基于集成学习的复杂仿真模型验证方法

首先,简要阐述了集成学习的基本方法;其次,提出了基于集成学习的复杂仿真模型验证方法框架;然后,为了挑选具有最大差异的基分类器,提出了基于惩罚因子的多样性筛选准则;最后,给出了集成分类系统的构造过程。

2.1 集成学习

可信度等级分类是一个典型的多类分类问题,一般是采用神经网络、支持向量机、决策树、贝叶斯方法等机器学习方法,训练单一分类器实现分类任务;但是单一分类器的准确率易受到训练样本标签准确性、样本规模、训练方法、参数等因素的影响,且算法稳定性较差。例如,将一组数据按照一定的比例划分为训练集与测试集,重复执行若干次;分别统计训练集或者测试集的分类准确率,同一种分类器的准确率结果可能差别较大。

集成学习[9-10]通过构建并结合多个学习器完成学习任务,也被称为多分类器系统或者集成分类系统。通过结合具有差异的基分类器,一方面,可以提高分类算法的稳定性;另一方面,可以提高算法的泛化能力。集成学习[10]可以表示为

(2)

式中,gm(y|x)表示单个学习模型(基分类器或者基模型);ωm表示调谐参数。

集成学习可以分为为两类,同构集成与异构集成。同构集成的典型代表是Bagging与Boosting。Bagging通过改变训练样本的抽样方式,并行生成不同的训练样本,用于多个同类分类器的训练,随机森林可以看作是对多个决策树模型进行Bagging集成。Boosting是通过序贯抽样与训练,逐步提升分类器性能,最终将多个基分类器进行融合。

异构集成是指将不同类型或者不同结构参数的分类器模型集成在一起,完成分类任务。构造准确率高且多样的分类器是集成学习算法成功的关键。异构学习在保证个体分类器的多样性方面具有一定的优势,在对不同结构分类器进行训练与性能测试基础上,筛选其中分类准确率高、多样性显著的模型加入异构分类系统,可以实现性能更好的集成分类系统。

在本文研究中,主要采用反向传播神经网络(back propagation neural network)[11-12]、误差校正输出编码(error correcting output coding, ECOC)支持向量机[13-14]作为基分类器。ECOC是一种将多个二分类器进行组合的框架,通过增加分类器个数,减少单个二分类器分类错误对整体分类结果的影响。

2.2 基于集成分类系统的复杂仿真模型验证方法框架

不同的机器学习方法具有不同的优势,神经网络可以拟合任意的非线性函数,但是学习精度的提高会带来过拟合的风险,导致泛化能力下降,此外其分类效果受到参数的影响。支持向量机可以利用少量的样本获得较为满意的结果,且算法稳定性较高,但是其精度受到一定的限制。通过对不同的机器学习模型进行集成,可以构建分类准确率更高,泛化能力更强,稳定性更好的集成分类系统。图2是本文提出的基于集成分类系统的复杂仿真模型验证方法框架。

图2 基于集成分类系统的复杂仿真模型验证方法框架Fig.2 Complex model validation method framework based onensemble classification system

基于集成分类系统的复杂仿真模型验证方法框架由特征提取模型和集成分类系统组成。特征提取模型采用多种分析方法对仿真时间序列与参考时间序列的相似性进行分析,之后将其规范化处理,合并后获得相似性度量向量。不同的相似性分析方法从不同的角度度量仿真时间序列与参考时间序列的相似性程度,将其作为学习模型的输入特征。集成分类系统利用多个基分类器分别进行相似性等级划分,之后进行多样性集成,获得可信度等级。

构造高质量的集成系统的关键是增强基分类器的多样性,利用不同的样本训练、采用不同类型的分类器模型或者不同拓扑结构的分类器、调整分类器训练参数等是增加基分类器多样性的主要手段。隐层节点个数不同的反向传播(back propagation,BP)神经网络、采用不同编码方式或者核函数的ECOC支持向量机,都可以认为是不同结构的分类器模型。

2.3 基于惩罚因子的多样性筛选准则

提高基分类器的多样性是集成学习的关键,可以使集成分类系统适应不同类型的样本,以提高分类的鲁棒性。在此,针对如何选择“好而不同”的基分类器,提出一种基于惩罚因子的多样性筛选准则。

不同分类器之间的多样性,可以利用分类器输出的差异程度来度量。假设U={u1,u2,…,uk}表示样本集的标签,即ui表示一组仿真数据与参考数据的可信度等级。将样本集划分为训练集与测试集,利用训练集,采用不同的分类器模型训练Q个分类器,然后在这Q个分类器中筛选出具有最好多样性的q个,之后进行集成。P={pv1,pv2,…,pv k}表示第ν个基分类器预测的样本集标签。

显然第一个分类器选择自由度最大,为了保证分类质量,选择训练集分类准确率最高的分类器;后续分类器的选择需要与第一个分类器进行多样性比较。对于第一个分类器分类错误的样本,希望第二个分类器可以尽可能多地预测正确,以对错误分类的样本进行部分纠正。距离度量可以一定程度上度量分类器的多样性,但是已选择的分类器对部分训练样本集E出现连续的分类错误,后续分类器选择就需要重点选择那些可以对样本集E的标签预测准确的分类器。为此,结合汉明距离,给出一种度量分类器多样性的筛选准则。

基于惩罚因子的多样性筛选准则为

γ,εi)[(pνi-ui)⊕(pτi-ui)]

(3)

式中,Eν,τ表示第ν个分类器与第τ个分类器间的差异程度;γ表示惩罚因子或者惩罚系数;εi为第i个样本分类错误的次数统计;A⊕B表示A与B的异或。f(γ,εi)用以度量第i个样本差异程度的权重,f(γ,εi)的形式可以是指数函数等非线性形式也可以是线性形式,可以灵活选择,但是需要注意∂f(γ,εi)/∂εi≤0,∂f(γ,εi)/∂γ≤0;即惩罚因子γ或者错误次数εi越大,f(γ,εi)越小,即其对差异的贡献越小。

2.4 集成分类系统构建过程

针对本文提出的集成分类系统的训练问题,在此给出基于IDEF0(ICAM definition for function modeling)[15-16]的集成系统构建过程模型,如图3所示。集成分类系统构建过程详细步骤如下。

图3 基于IDEF0的集成分类系统构建过程Fig.3 Construction process of ensemble classification systems based on IDEF0

步骤1构建基础数据集与相似性分析准则集;基础数据集中的每一个样本包含一组仿真时间序列与参考时间序列。本文主要采用的相似性度量方法包括绝对误差度量、相对误差度量、其他相似性度量3种类型。

绝对误差度量方法包括平均绝对误差(mean absolute error, MSE)、均方误差(root mean square error, RMSE)、切比雪夫距离等;相对误差度量方法包括相对平均绝对误差(relative mean absolute error, RMAE)、平均绝对相对误差(mean absolute relative error, MARE)、最大绝对相对误差(maximum absolute relative error, MaARE)、相对均方误差(relative root mean square error, RRMSE)、Theil不等系数(Theil’ inequality coefficient,TIC)法;其他相似性度量方法包括余弦相似度,线性相关系数、SVARE(standard variance of absolute relative error)法等。上述大部分方法可以在综述性文献[2-4]找到,在此仅给出MaARE法、SVARE法计算公式。

(4)

(5)

步骤2基础数据集的多准则分析;利用所有的相似性分析方法对每一组仿真时间序列与参考时间序列进行分析。

步骤3基础数据的相似性等级划分;对于已经具有可信度数值的基础数据,根据模糊隶属度函数[8],将可信度结果转换为可信度(相似性)等级。对于未评估的数据,采用群组决策法[17],邀请多位主题专家与分析人员进行主观评估,得到相似性等级标签。

步骤4样本集规范化处理;一组基础数据的所有相似性分析结果与相似性等级构成一个样本。由于不同的相似性分析结果值域差异较大,会影响训练的收敛速度。采用式(6)对样本集进行规范化处理。

(6)

式中,α为调节系数;Q为某一种相似性分析方法的度量结果;Qmin为所有样本采用该相似性分析方法获得分析结果最小值;Qmax为所有样本采用该相似性分析方法获得分析结果最大值;Quniform为归一化结果;Quniform∈[0,1]。

步骤5单一分类器的训练;按照一定的比例将样本集划分为训练集与测试集,训练Q个不同类型或者结构参数不同的分类器。

步骤6分类系统的多样性集成;首先选择训练集分类准确率最高的基分类器,之后利用基于惩罚因子的分类器多样性筛选准则选择多样性差异最大的前T个分类器,将T个分类器中分类准确率最高的作为集成分类系统的下一个基分类器,重复上述过程,直到挑选出所有q个基分类器。采用式(1)进行集成,可以采用均权或者以训练集分类准确率为参考进行权重分配。利用测试集进行性能测试,若达到要求,则训练结束;否则,可以选择调整集成过程参数,或者回到步骤5,重新进行训练。

每个基分类器的权重计算式为

,m=1,2,…,q

(7)

步骤7集成分类系统的应用;利用训练好的分类系统计算新样本的可信度。

对于集成分类系统中单一分类器的训练问题(BP神经网络与ECOC支持向量机),可以参考文献[12,14-15]。

3 应用实例

为了检验基于集成学习的复杂仿真模型验证方法的有效性,选择飞行器六自由度动力学仿真数据及相应参考系统的试验数据作为基础数据集(675组);包括飞行器位置、速度、姿态等信息,每一组数据包含相同想定下的仿真时间序列与参考时间序列。

选择第2.4节列出的相似性分析方法进行多准则分析,并对相似性等级进行标记及规范化处理。下面首先对单个分类器可信度等级分类性能进行对比;之后利用本文提出的多样性筛选准则,对构建的改进集成分类系统与一般集成分类系统的可信度等级分类性能进行对比。集成学习的优势体现在多次重复训练时,可信度等级分类准确率统计性能的提升;因此,下文着重对不同分类方法的可信度等级分类准确率的方差、均值、分位数等指标进行对比分析。

3.1 单个分类器的可信度等级分类性能对比

选择5类分类器模型,对性能进行对比分析。

(1) 3层结构BP神经网络,输入层、隐层、输出层神经元个数分别为12-H-1,设置隐层神经元个数H分别为6、8、10。

(2) ECOC支持向量机,采用高斯核函数,编码方式[14]采用1对1编码(one vs one, 标记为code1)与1对多编码(one vs all, 标记为code2)。

样本集按照一定比例随机划分为训练集(575组,标记为Tr)与测试集(100组,标记为Te),对不同的分类器模型进行训练,重复运行50次,得到BP神经网络、ECOC支持向量机的分类准确率箱线图如图4所示。表1为不同类型或者结构参数的分类器性能对比。

图4 不同类型或者结构参数的分类器准确率箱线图Fig.4 Classification accuracy boxplot of classifiers with different type or topology parameters

准确率/%BP神经网络Tr(H=6)Te(H=6)Tr(H=8)Te(H=8)Tr(H=10)Te(H=10)ECOC支持向量机Tr(code1)Te(code1)Tr(code2)Te(code2)均值88.7283.9889.7184.6890.2584.8287.6876.6789.5775.60方差10.5315.699.4915.496.3211.660.858.761.917.99中位数89.4784.0090.5385.0090.1185.0087.7977.0089.5876.00最小值78.9569.0078.9574.0085.2673.0085.8970.5086.7469.00最大值93.4792.0093.8993.0094.9590.0090.5381.5092.6380.50

注:(1)Tr表示训练集,Te表示测试集;H表示隐层神经元个数;code1表示one vs one编码,code2表示one vs all编码;

(2) 表中加粗的数字表示每一行中训练集或者测试集的最佳值,方差越小表示算法越稳定,其余统计指标越大越好。

根据图4以及表1中不同结构分类器的可信度等级分类性能统计,整体上,同一分类器的对训练集的可信度等级分类准确率要高于测试集分类准确率,即分类器存在过拟合的风险;对于不同结构参数的BP神经网络或者采用不同编码方式的ECOC支持向量机,其可信度等级分类准确率也存在一定的差异(均值、方差、分位数等)。显然,不同类型的机器学习模型各有优势,隐层8个神经元的BP神经网络整体上性能最佳,但是隐层10个神经元的BP神经网络在测试集上效果更好,支持向量机在算法稳定性表现较好。

3.2 集成分类系统的可信度等级分类性能对比

为了检验基于惩罚因子的多样性筛选准则的有效性,采用以下两种集成方法构建集成分类系统,并对其可信度等级分类性能进行对比。

(1) 选择第3.1节中5类模型,每类分类器模型训练10个(总计50个),利用多样性筛选准则从中选择5个进行集成,得到相应的改进集成分类系统(improved ensemble classification system, IECS)。

(2) 每类分类器模型生成一个进行集成,得到一般集成分类系统(general ensemble classification system, GECS)。

对上述两种集成方法分别重复运行20次,统计可信度等级分类准确率。两种集成分类系统箱线图如图5所示,具体的性能统计如表2所示。根据箱线图及性能统计,采用本文提出的多样性筛选准则构建的IECS,训练集分类准确率均值达到了92.95%,测试集分类准确率均值达到了87.30%,其分类性能超过了文献[6]中PNN的准确率75%～80%及文献[18]中ECOC支持向量机的准确率82.3%。

采用多样性筛选准则构建的IECS在可信度等级分类准确率的均值、方差、分位数等方面均优于GECS,这反映了本文提出的方法在准确率与算法稳定性方面要超过了一般集成学习方法。

图5 IECS与GECS的分类准确率箱线图Fig.5 Classification accuracy boxplot of IECS and GECS

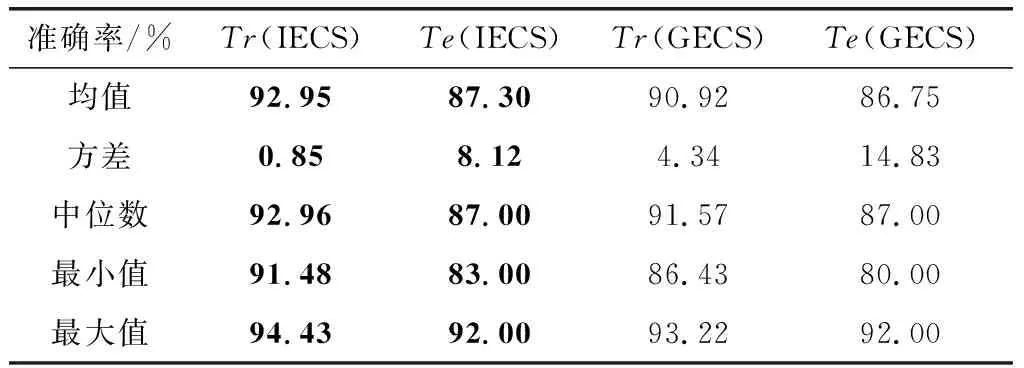
准确率/%Tr(IECS)Te(IECS)Tr(GECS)Te(GECS)均值92.9587.3090.9286.75方差0.858.124.3414.83中位数92.9687.0091.5787.00最小值91.4883.0086.4380.00最大值94.4392.0093.2292.00

此外,从表1与表2中的最值统计,对于单个BP神经网络或支持向量机,可信度等级分类准确率分布在69%～94%,显然其稳定性较差,在应用过程中存在风险。IECS可信度等级分类准确率集中在83%～94%,GECS可信度等级分类准确率集中在80%～93%;相对神经网络、支持向量机与GECS,IECS在整体分类准确率与算法稳定性方面均有提升,这意味着在应用过程中,对于不同的训练数据,采用本文的方法构建的IECS更容易获得较好的可信度等级分类结果。

3.3 结果分析

为了更加直观地展示可信度等级分类效果,图6与图7给出了改进集成分类系统的训练集(575组)与测试集(100组)分类结果。蓝色数字为分类正确的样本个数以及所占比例,红色数字为分类错误的样本个数以及所占比例;右下角灰色方块内为整体的可信度等级分类准确率及错误率。集成分类系统对训练集与测试集分类准确率分别达到了92.9%与92%,同时对于分类错误的样本,预测标签与样本标签的误差绝对值均为1(双线六边形边框内)。上述分析结果进一步证明本文提出的集成分类系统构建方法以及基于惩罚因子的多样性筛选准则的有效性。

利用机器学习构建通用的数据相似性分析方法,进而借助高性能计算机、云计算等技术实现对海量数据的分析,可以极大的提高复杂仿真模型验证的效率。不同的机器学习模型具有不同的优势,集成学习一方面将不同类型、不同结构参数的机器学习模型有机结合成一个整体,完成相应的学习任务;另一方面,集成学习构建的系统在一定程度上融合了各个基模型的优势。

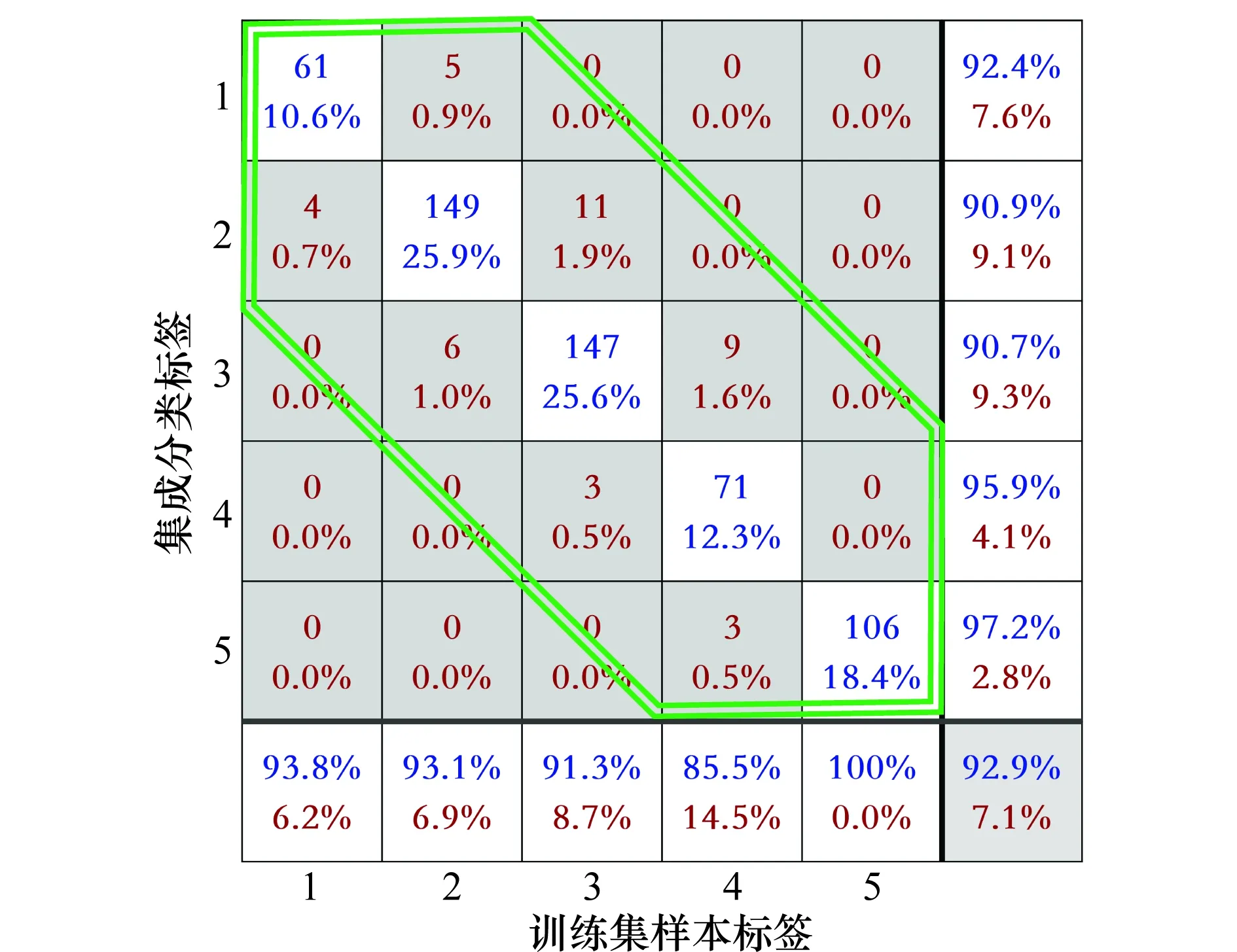
图6 训练集分类结果Fig.6 Classification result of training datasets

图7 测试集分类结果Fig.7 Classification result of test datasets

4 结 论

海量数据的相似性分析是复杂仿真模型验证面临的挑战之一,利用机器学习方法设计通用的相似性分析方法,是应对这一挑战的有效解决途径。本文在神经网络、支持向量机与集成学习等方法的基础上,提出了一种基于惩罚因子的分类器多样性筛选准则,用于构建分类性能更好的集成分类系统。应用结果表明,本文提出的用于相似性等级分类的改进集成分类系统性能优于一般集成分类系统以及单个机器学习方法获得的分类模型。

利用机器学习方法对数据相似性等级进行划分,可以降低评估成本,提高模型验证工作的效率。此外,集成分类系统在不断的应用过程中,可以对其结构及其参数进行优化,进一步提高其性能。