OFDM/OQAM系统限幅补偿IAM信道估计方法

吴 鹏, 陈西宏, 邱上飞, 张 凯

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

正交频分复用(orthogonal frequency division multiplexing,OFDM)技术[1]是多载波通信技术的一种,该技术将高速传输的数据分散到多个正交的子载波上传输,使得每个子载波上的符号速率大大降低。因此,OFDM相比单载波通信技术而言,有着很强的抵抗频率选择性衰落的能力。但是为了抵抗符号间干扰,OFDM技术需要引入循环前缀,降低了频谱效率。此外,OFDM技术使用矩形窗滤波器进行整形,带外辐射比较严重,使得OFDM系统对载波频偏和多普勒频偏非常敏感,易产生子载波间干扰(inter carrier interference,ICI)。

OFDM技术的不足是其自身固有属性造成的,即使采取一些措施可以改善其系统性能,但是无法从根本上解决这些问题。基于偏移正交幅度调制的正交频分复用(OFDM/offset quadrature amplitude modulation,OFDM/OQAM)技术[2]的提出,将多载波通信技术带入了一个新的方向。OFDM/OQAM技术是基于滤波器组的多载波(filter bank multi-carrier,FBMC)技术的一种,由于引入了良好的时频聚焦性能的滤波器,OFDM/OQAM系统在不需要循环前缀的情况下拥有更好的抗ICI和符号间干扰(inter-symbol interference,ISI)的能力,提高了频谱效率[3]。其代价则是放宽了符号间的正交性,使其仅仅满足实数域的正交条件。这种特性不可避免地会给相邻的符号和子载波之间带来固有的虚部干扰,这种干扰会对系统的同步、信道估计和均衡过程带来很大影响。此外,作为一种多载波技术,较高的峰均比(peak-to-average power ratio,PAPR)也是OFDM/OQAM技术固有的缺点之一。

OFDM/OQAM系统关键技术主要集中在系统设计、滤波器设计、信道估计、时频同步技术、PAPR降低等方面。近年来,时频偏与信道的联合估计[4-5]、信道估计联合PAPR降低[6]等联合技术成为人们研究的热点。

信道估计技术是OFDM/OQAM系统十分重要的一环,信道估计的准确度决定了系统的比特误码率(bit error ratio,BER)性能。信道估计的研究文献大都集中在基于导频的信道估计,根据导频结构的不同可分为块状导频[7-10]和格状导频[11-13]。块状导频法主要有成对导频(pair of pilots,POP)法[8]、干扰近似法(interference approximation method,IAM)[9]和干扰消除法(interference cancellation method,ICM)[10]。其中,ICM是通过设计导频结构将虚部干扰消除,而IAM的特点是对虚部干扰加以利用,将干扰和导频符号结合成“伪导频”,理论上讲,伪导频功率越大,估计精度越高。但是伪导频功率越大,产生的PAPR越高。当信号的幅值超过高功率放大器(high power amplifier, HPA)的放大范围时,信号就会产生非线性失真,严重影响系统的性能。

本文考虑HPA对导频信号的影响,在原有系统模型基础上进行修正,增加了发射机和接收机环节,分析了信号产生非线性失真后系统的信道估计归一化均方误差(normalized mean square error,NMSE)和BER性能,并针对这种影响提出一种限幅补偿的解决方法。

1 OFDM/OQAM系统模型

在OFDM系统中,子载波上传输的是复数符号。OFDM/OQAM技术则是将OFDM系统中传输的复数符号的实部和虚部拆解为两个实数,并相互交错半个符号周期之后在实数域进行传输。在考虑循环前缀的情况下,OQAM/OFDM系统比OFDM系统有着更高的传输效率。而且,OFDM/OQAM系统的实现同OFDM系统类似,可以基于快速傅里叶变换/反变换(fast Fourier transformation/inverse fast Fourier transformation,FFT/IFFT)实现。

OFDM/OQAM系统发送信号的时域基带形式[2]为

(1)

式中,am,n为时频格点(m,n)上传输的实值符号；gm,n(t)为原型滤波器生成的基函数:

gm,n(t)=g(t-nτ0)ej2πmF0tejφm,n

(2)

式中,τ0为符号间隔;F0为子载波间隔。

τ0F0=1/2

(3)

φm,n为符号的相位,本文取

(4)

发送信号经过无线信道后,被接收端接收,则接收信号表达式为

r(t)=h(t,τ)⊗s(t)+η(t)=

(5)

式中,h(t,τ)为信道冲击响应;η(t)为高斯白噪声;⊗为卷积运算;Δ为信道最大时延。

假设基函数gm,n(t)满足正交条件:

δm,pδn,q

(6)

式中,〈·〉R为实内积运算;R(·)为取实部运算;δ为Kronecker函数,有

(7)

假设τ0≫Δ,则接收端解调信号的表达式为

(8)

式中,Hm,n为时频格点(m,n)处的信道频率响应。解调符号可表示为

,gm′,n′〉=

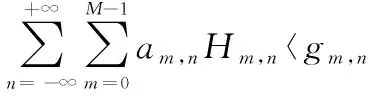
(9)

若频率响应的估计值等于真实值,则可用简单的迫零均衡将符号正确地解调出来:

,gm′,n′〉+

(10)

式中,I为系统固有的虚部干扰。

以上是传统的OFDM/OQAM系统的工作原理,但是在实际的信号发送和接收过程中,信号的功率若超过HPA的线性范围,则会造成非线性失真。典型的HPA模型[14]有软限幅(soft limiter, SL)模型、固态功率放大器(solid state power amplifier, SSPA)模型、立方多项式(cubic polynomial, CP)模型和行波管放大器(traveling-wave tube, TWT)模型4种。SL模型是文献中广泛使用的HPA模型,本文的分析全部采用此模型。其放大特性为

(11)

式中,g(x(t))为经过HPA的输出信号;x(t)为输入信号的时域波形;A为HPA的饱和值;φ(t)为t时刻信号的相位。可以看出,HPA的SL模型只改变信号的幅度,不改变信号的相位。

由于HPA对信号的影响直接作用在信号的时域波形上,因此在原有基于FFT/IFFT实现的系统模型基础上,加入HPA对信号影响的环节非常有必要。修正后的系统模型如图1所示。

图1 修正的OFDM/OQAM系统模型Fig.1 Modified OFDM/OQAM system module

后文分析、仿真所用的系统模型均采用本节修正后的模型。

2 IAM信道估计方法

IAM信道估计方法将导频符号及其一阶邻域的符号进行合理设计,使得导频点受到的固有干扰就会被确定。在信道估计的过程中将固有干扰和导频点共同组成一个伪导频。设虚部干扰为up,q,导频点为ap,q,则伪导频为

cp,q=ap,q+jup,q

(12)

对信道进行最小二乘估计,可得信道的估计值为

(13)

2.1 导频结构

IAM导频结构[7]包括IAM-R、IAM-I、IAM-C、E-IAM-C,其中,IAM-I是IAM-C的一种特殊情况。其各自的结构如图2所示。

图2 IAM导频结构Fig.2 IAM pilot structure

以α=2的扩展高斯函数(extended Guassian function,EGF)滤波器为例,设导频ap,q±1、ap±1,q、ap±1,q±1和ap±1,q±2对导频点ap,q的干扰系数分别为a、b、c和d,干扰系数[16]如表1所示。

表1 导频点周围干扰系数

设导频点ap,q的功率为P,由此计算出各种IAM导频结构的伪导频功率计算方法和功率值[16]如表2所示。其中,IAM-I导频结构有奇数列导频结构和偶数列导频结构两种,不同的IAM-I导频结构有不同的伪导频功率值。

表2 不同IAM导频结构的伪导频功率

2.2 IAM导频对发送信号的影响

导频插入方式选择前导方法,即在数据符号之前插入导频,子载波数M=2 048,符号数n=80,EGF滤波器α=2,滤波器长度L=4T0,其中T0为一个符号周期,IFFT点数为Fs=2 048,纠错方式为前向纠错码,码率为0.5,采样频率为9.14 MHz,信道模型为多径衰落模型,多径数为6,各径的时延向量为[-3,0,2,4,7,11]μs,信号增益向量为[-6,0,-7,-22,-16,-20]dB。

由于IAM-I是IAM-C的特殊情况,因此仿真时不考虑IAM-I。设平均功率为0 dB,对发送信号功率做归一化处理,无导频插入的OFDM/OQAM信号的时域波形如图3所示。插入IAM-R、IAM-C和E-IAM-C导频结构后的OFDM/OQAM信号归一化功率图分别如图4～图6所示。

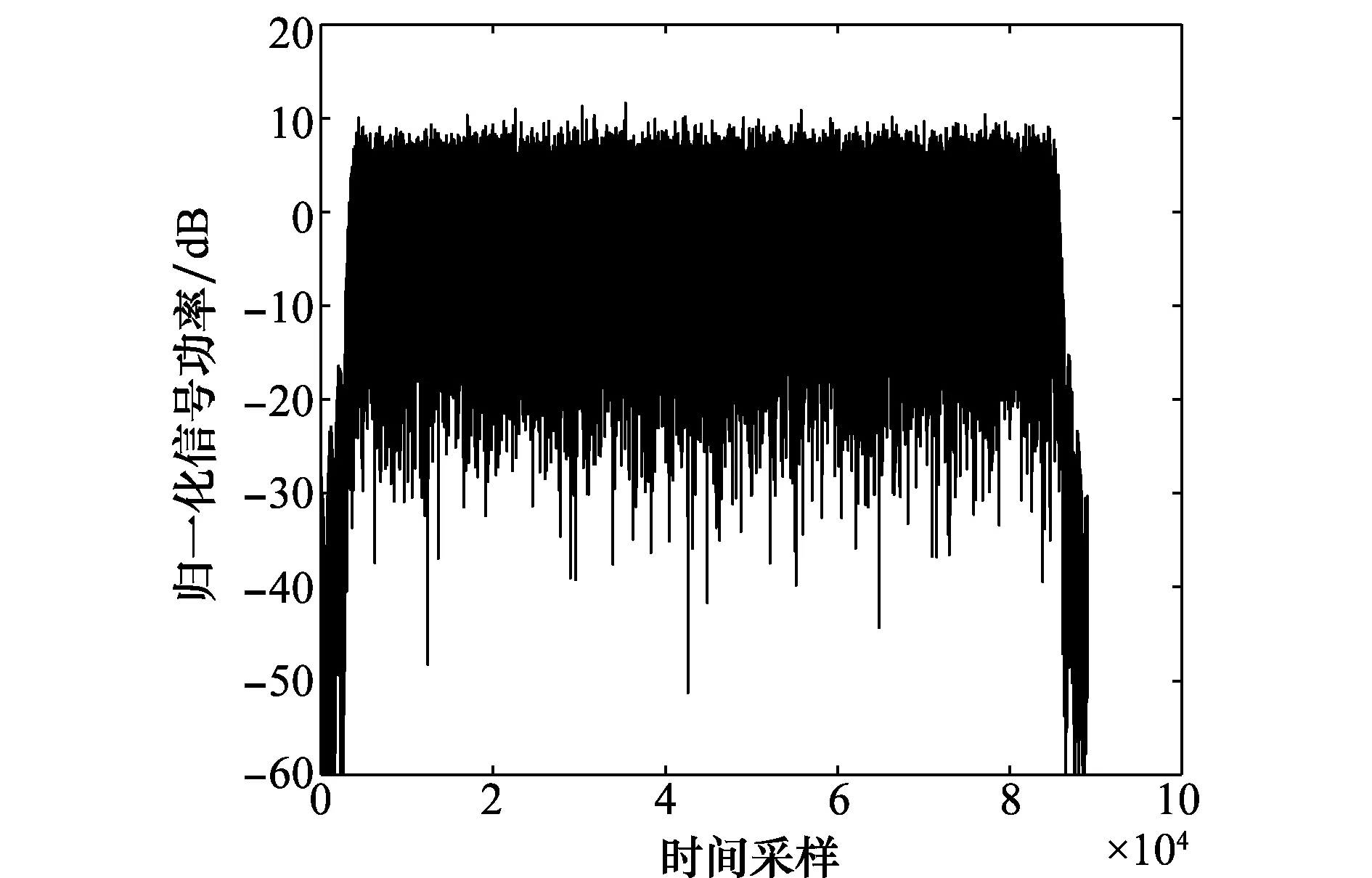
图3 无导频OFDM/OQAM信号归一化功率Fig.3 Normalized power of OFDM/OQAM signal without pilot

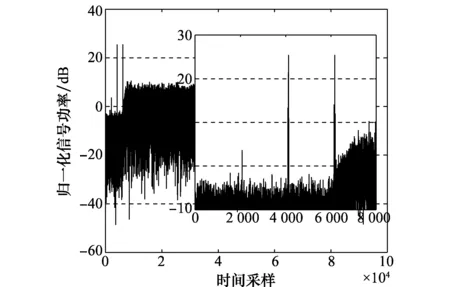
图4 插入IAM-R导频的OFDM/OQAM信号归一化功率Fig.4 Normalized power of OFDM/OQAM signal with IAM-R pilot

图5 插入IAM-C导频的OFDM/OQAM信号归一化功率Fig.5 Normalized power of OFDM/OQAM signal with IAM-C pilot

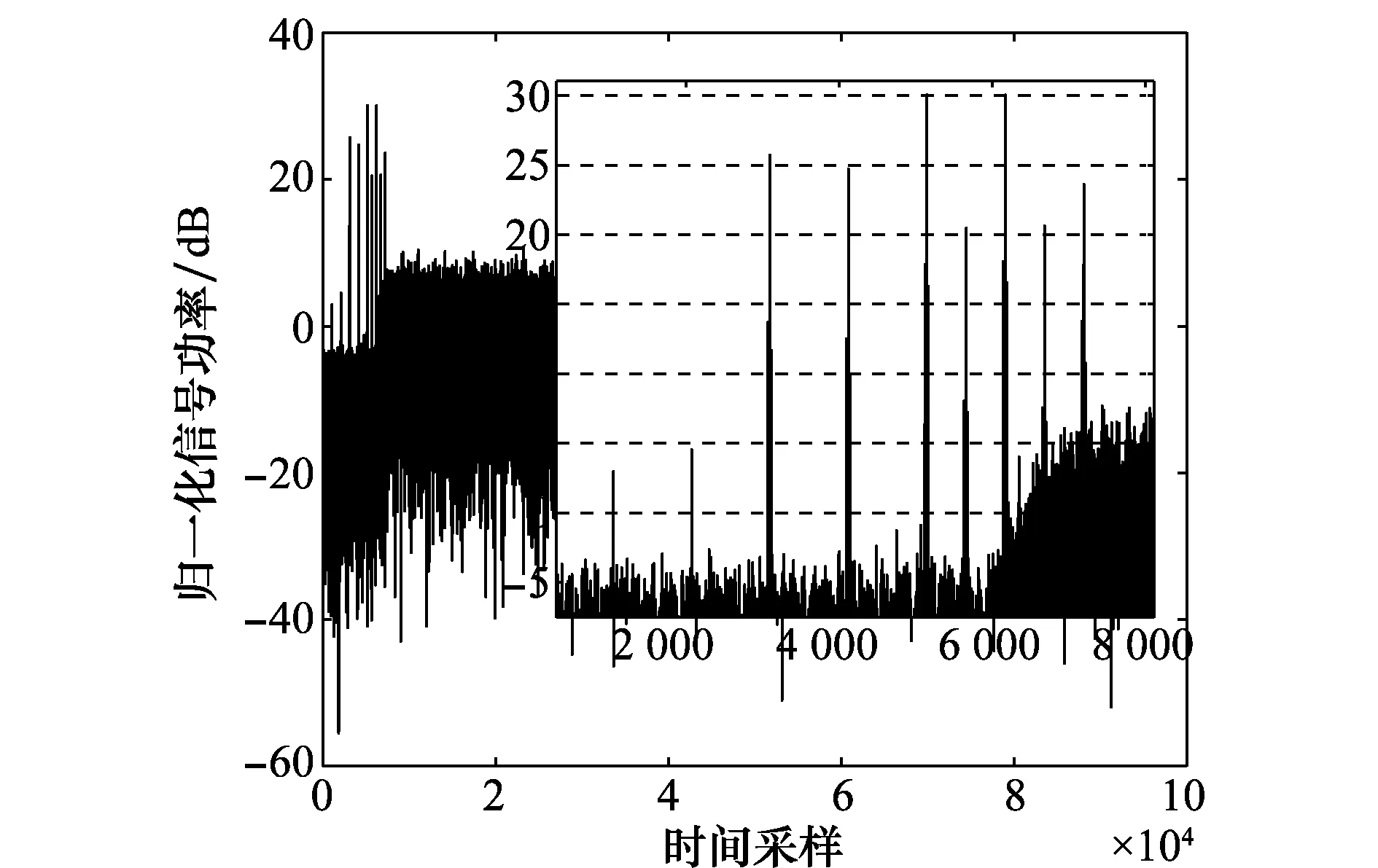
图6 插入E-IAM-C导频的OFDM/OQAM信号归一化功率Fig.6 Normalized power of OFDM/OQAM signal with E-IAM-C pilot

图4、图5和图6分别为插入不同IAM导频结构的导频后的OFDM/OQAM信号归一化功率图,可以看出,3种插入导频方式都会使发送信号的某些时刻信号功率过高,信号峰值功率甚至超过30 dB,而且随着伪导频功率的提升,高功率的点数也有所增加。这些高功率的信号通过HPA时会引起严重的限幅失真。接下来研究限幅失真对系统BER性能和信道估计NMSE性能的影响。

2.3 HPA对系统性能的影响

实际的HPA对信号的限幅影响比较复杂,限幅后的信号会产生三阶、五阶等高阶互调分量,其中三阶互调分量直接引起带内干扰,使系统误码率性能下降,五阶等高阶分量将引起带外辐射的增加。本文将HPA的限幅过程简化,忽略高阶互调分量产生的影响。

仿真时使用HPA的SL模型对信号进行限幅作用,设置限幅10dB、20dB、30dB和无限幅,仿真参数与第2.2节相同,计算系统的BER和信道估计NMSE,仿真结果如图7和图8所示。

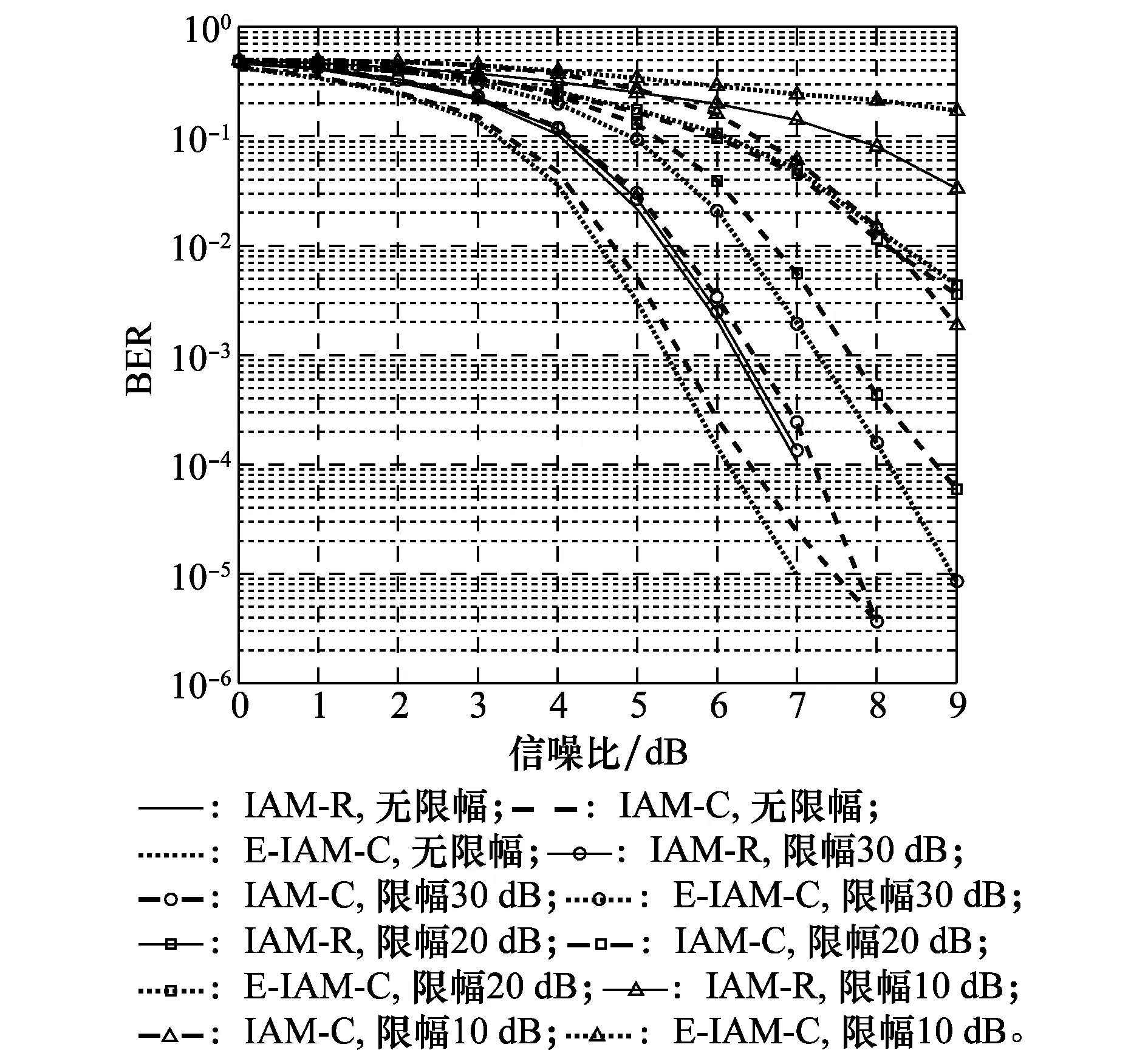
图7 不同限幅门限下系统BER性能Fig.7 BER performance of the system in different clipping threshold

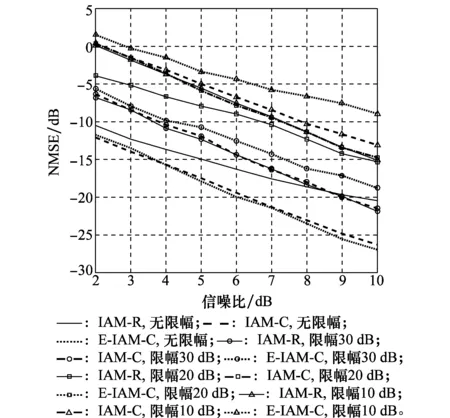
图8 不同限幅门限下的信道估计NMSE性能Fig.8 NMSE performance of the channel estimation in differentclipping threshold

由图7可以看出,HPA对信号的限幅作用使得系统的BER性能迅速恶化,限幅门限为20 dB时,在信噪比为8 dB时,IAM-C和E-IAM-C导频下的系统误码率只有10-2,限幅门限为10 dB时,E-IAM-C导频下的系统已出现严重的误码平层,无法满足系统的信息传输要求。造成系统误码率性能恶化的原因正是导频信息被破坏,限幅门限越低,导频信息被破坏的越严重。从图8中可以看出,相对3种结构,信道估计精度最高的E-IAM-C方法受限幅影响最严重。

3 IAM导频PAPR性能

3.1 PAPR与互补累积分布函数

OFDM/OQAM信号是若干不同频率信号的叠加,发送信号的幅度具有较大的动态范围。而IAM导频是人工设计的符号序列,更加容易使各载波通过相同的相位叠加,产生较高瞬时功率。PAPR用来描述信号的变化特性,设发送信号为s(t),S[n]为其采样,则PAPR定义[17]为

(14)

互补累积分布函数(complementary cumulative distribution function,CCDF)是描述多载波系统PAPR性能的常用函数,其定义是,信号的PAPR大于某一门限值γ的概率。在使用EGF滤波器的OFDM/OQAM系统中,CCDF的表达式[17]为

Pr(PAPR>γ)=1-(1-e-γ)N

(15)

利用第2节的仿真参数,绘出3种IAM导频结构下的OFDM/OQAM发送信号的CCDF图像，如图9所示。

图9 不同IAM导频结构的OFDM/OQAM信号CCDFFig.9 CCDF of OFDM/OQAM signal in different IAM pilot structures

由图9可以看出,插入导频后对整体发送信号的CCDF没有造成太大影响,通过CCDF不能很好地反映出导频的PAPR性能。由于本次仿真中,导频符号只占3列时频格点,经过IFFT后,导频的时域采样点占全部信号采样点的比例为

.106

(16)

虽然导频的插入引起了某些时刻功率值的增加,但是相对于整体发送信号来说,这些高功率的时刻是很少的,而CCDF描述的正是全部信号中超过某一门限的概率,导频的插入对于此概率的影响很小,因此,导频的PAPR性能并不能直接从CCDF反映出来。基于此,本文提出一种局部互补累积分布函数(part-CCDF,p-CCDF)来反映导频的PAPR性能。

3.2 局部互补累积分布函数

p-CCDF的定义为:时域上导频采样点的值与发送信号的比值超过某一门限γ的概率。p-CCDF与CCDF的区别在于,选取峰值信号采样点时,只选取导频符号经IFFT变换后对应的采样点而非全部采样点,而信号均值仍采用全部发送信号的均值。设Sp[n]为导频采样点,则PAPRp为

(17)

p-CCDF的计算式为

Pr(PAPRp>γ)=1-(1-e-γ)N

(18)

由于IAM导频包含3列符号,计算p-CCDF时选取前(L/T0+(3-1)/2)Fs个采样点进行概率的计算,得p-CCDF图像如图10所示。

图10 不同IAM导频结构的导频p-CCDFFig.10 p-CCDF of pilot in different IAM pilot strutures

从图10可以看出,通过p-CCDF可以清楚地展示出3种IAM导频的PAPR性能,E-IAM-C的PAPR性能最差,因此受HPA的限幅影响越严重。虽然，理论上基于E-IAM-C导频结构的信道估计有较好的估计精度,但是受到HPA限幅影响,使OFDM/OQAM系统性能变得更差。

由于HPA对信号的限幅影响类似于多载波信号PAPR降低中的限幅法,受限幅法中抵消和补偿限幅影响方法的启发,考虑如何将限幅法中对信号的限幅补偿应用到对导频的补偿中来。

4 IAM信道估计限幅补偿方法

多载波系统中常用的PAPR抑制方法分为畸变类技术[18-20]、编码类技术[21]和概率类技术[22-23]。编码类技术是通过编码手段避免大功率信号的出现,由于导频序列是预先设定好的导频序列,因此编码类技术不适合用于导频峰均比的降低。概率类技术是利用不同的加扰序列对多载波符号进行加权处理,并选择PAPR最小的进行发射。由于导频符号所占信号的比重很小,所以概率类技术也不是理想的方法。

限幅法是一种信号畸变类方法,简单有效。由于限幅法会造成系统带外辐射增加和引入限幅噪声,在降低多载波信号PAPR时,限制带外辐射和抵消限幅噪声非常困难。但是,导频是设定好的数据符号,这个特点使得导频信号的限幅补偿容易的多。

4.1 限幅补偿方法

文献[18]针对OFDM/OQAM系统发送信号PAPR抑制问题,利用发送信号幅度服从复高斯分布这一特点,通过迭代的方法恢复限幅噪声,使得系统的PAPR性能和BER性能都得到了很好地改善。文献[19]采用迭代的限幅滤波和带外辐射抑制方法降低OFDM信号的PAPR,并采用基于压缩感知(compressive sensing,CS)的半解析重构限幅噪声来提高系统的BER性能。文献[20]提出了优化迭代限幅滤波算法(optimized iterative clipping and filtering,OICF),该算法使用更低的迭代次数,更有效地抑制了带外辐射。文献[24]采用限幅标记的方法,将OFDM信号的限幅位置信息记录下来并发送给接收端,接收端对限幅后的信号进行补偿。该方法容易实现,但是发送的位置信息占用了额外的频谱资源,且补偿倍数单一,不能完整地恢复信号。

相比发送信号,导频符号是预先设定好的,IFFT之后导频信号的幅度信息也是已知的,因此,只要提前计算好导频信号的幅值和设置限幅门限,对接收端导频信号进行补偿比较容易,设置限幅门限也可以降低发送信号的PAPR，具体过程如下。

步骤1计算导频符号的IFFT,计算结果为向量ε,向量长度为n=(L/T0+(3-1)/2)Fs。

,i=1,2,…,n

(19)

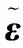
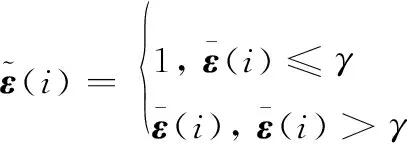
,i=1,2,…,n

(20)

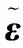
,i=1,2,…,n

(21)

该方法不需要进行迭代和传输额外的补偿信息,不会增加系统的复杂度和信号传输效率。下一节通过仿真来验证方法的有效性。

4.2 仿真分析

采用第2.2节仿真参数,第4.1节提出的补偿方法仿真结果如图11和图12所示。采用的导频结构为IAM-R、IAM-C和E-IAM-C,计算系统的BER性能和NMSE性能。

图11和图12表明，本文提出的导频限幅补偿方法能够改善系统的BER性能和信道估计的NMSE性能。从图11和图12中可以看出,信噪比为7 dB时,20 dB补偿下的IAM-R、IAM-C和E-IAM-C导频结构系统BER分别改善到了10-4、10-4和10-5,NMSE性能分别改善了4 dB、9 dB和15 dB;信噪比为8 dB时,10 dB补偿下IAM-R、IAM-C和E-IAM-C导频结构系统BER分别改善到了10-2、10-3和10-4,NMSE性能分别改善了3 dB、6 dB和11 dB。导频结构的PAPR越高,受到HPA的影响越严重,补偿效果越好。但是，如果HPA的限幅门限过低,限幅过程将会对导频信息和传输数据同时造成严重的非线性破坏,即使采用补偿手段,补偿效果也受到一定限制。

5 结 论

针对OFDM/OQAM系统的IAM信道估计方法,研究了收发机HPA对信号的限幅影响,提出了导频PAPR和p-CCDF。仿真结果表明,IAM导频结构中,伪导频功率越高,导频PAPR越高,受到HPA的限幅影响越严重,系统的BER性能和信道估计精度越低。为了补偿这种限幅影响,提出了一种导频限幅补偿方法,该方法不需要传输额外的补偿信息,不影响系统的传输效率。仿真结果显示,补偿方法有一定的作用。此外,导频信息受到HPA限幅影响越严重,补偿的效果越好。

本文在研究HPA对信号限幅影响时忽略了带外辐射的增加,因此补偿效果还有增加的空间。如果能够将HPA限幅导致的信号带外辐射考虑在内,结合带外辐射抑制技术,补偿精度将会进一步提升。