异构UAV编队反雷达作战中任务分配方法

林君灿, 贾高伟, 侯中喜

(国防科技大学空天科学学院, 湖南 长沙 410073)

0 引 言

防空雷达是空情预警的核心装备,各类防空雷达装备技术的快速发展,使得传统电子战飞机的作战效能大大降低。同时,传统的电子战飞机雷达反射截面积较大,导致隐身性能差,易被发现与攻击。

小型无人飞行器系统具有尺寸小、成本低、突防能力强等特点,且雷达散射回波通常较弱,能够遂行复杂电磁环境下的电子干扰、诱骗及攻击任务。同时,随着无人机自主控制能力的提高,无人机编队战术引起了广泛关注。将不同载荷不同平台的无人机编队(异构无人机编队)用于对敌方雷达阵地实施侦察、定位、打击、评估,是摧毁敌方防空预警系统的重要作战样式,受到国内外的高度关注。

在异构无人机编队的应用中,任务分配是顶层的规划设计,研究意义重要[1]。

国外的研究团队设计建立了多类任务分配模型,包括车辆路径问题(vehicle routing problem,VRP)模型[2]、多旅行商问题(multiple traveling salesman problem,MTSP)模型[3]、混合整数线性规划(mixed integer linear programming,MILP)模型[4]等。应用MILP方法可以纳入时间等连续约束条件,可以精确得到更加符合实际情况下的任务分配问题的最优解。文献[5]利用MILP模型分析解决了多个相同无人机(同构无人机)执行广域搜索地攻击任务分配问题。此外,文献[6]将遗传算法应用于多无人机任务分配问题上,凸显了遗传算法的计算时效性。

国内方面,文献[7]结合基于时间窗的MILP任务分配模型,给出多架同构无人机协同对地攻击优化问题的任务分配方案。文献[8]在MILP模型中加入目标的威胁因素, 提高了完成任务的准确性。文献[9]通过对适应度值做了标定,改进了遗传算法,解决了多约束下多无人机协同任务分配问题。文献[10]采用一种改进的非支配排序遗传算法,任务分配结果的Pareto最优解集。

对比发现,在多无人机任务分配方法研究中,MILP和遗传算法是两类常用的方法[11-15]。现有的MILP类方法大多应用在同构无人机编队间的任务分配,未考虑异构无人机编队在飞行平台差异化、载荷功能差异化、时空协同复杂化方面的影响[16];而现有应用于任务分配的遗传算法及其改进型,未考虑异构无人机编队的任务功能多样化以及严格的时间窗约束。为了解决异构无人机编队复杂的任务分配问题,有必要对现有MILP方法和遗传算法进行改进。本文提出了一种基于时间窗的异构无人机编队MILP模型,建立了无人机之间、执行任务之间合理的协同约束关系。此外,提出了基于时间窗的多层编码遗传算法实现异构无人机编队任务分配,结合时空四维约束,清晰地表达出异构无人机编队执行任务时的时序关系。

1 问题描述

异构无人机编队对敌方雷达阵地进行攻击作战过程中,编队内的无人机能够独立进行搜索、分类、攻击、评估等任务。当编队中任何一架无人机进行信息更新(例如发现一个新雷达目标时),编队内的无人机均能共享该信息。当发现潜在或可疑的目标时,启动分类任务。分类是从另一个观察视角对目标进行第二次搜索探测,从而提高目标识别的置信水平。待可疑目标被分类确认后,对其执行攻击任务。在本想定中,执行攻击任务的无人机通过自身携带的弹药部摧毁目标。

一般地,对雷达站目标的打击需要在特定的时间窗口内进行(例如雷达的开机时间内)。随后还需由另一架飞机进行探测核实以确认目标是否已被摧毁。

任务描述如下:在某作战区域内,我方区域内分布有V架无人机,敌方区域上分布N个地面雷达站,我方无人机对敌方区域进行搜索,在被探测到的敌方雷达站上依次执行分类,攻击和毁伤评估任务,在满足无人机分配逻辑和任务到达先后次序的前提下,总的任务执行时间最小,没有分配到任务或完成任务的无人机继续对目标进行搜索。

结合实际作战情况,想定如下:①地面雷达站为固定目标,位置坐标均已知,无人机当前位置坐标也已知;②同一个目标上的任务执行顺序为:先分类后攻击再评估;③同一架无人机在同一个目标上最多执行两次任务,即允许执行分类任务后立刻执行攻击任务;④无人机攻击目标后自爆自毁,将不再接受任务分配;⑤由于飞行时间远大于执行任务的时间,故忽略任务执行时间。

2 基于MILP模型的任务分配

基于MILP模型的任务分配描述如下,假设有N+V+1个节点:N个目标节点、V个无人机源节点和一个搜索节点。节点1,2,…,N对应N个目标位置,节点N+1,N+2,…,N+V对应V个无人机源节点,节点N+V+1是搜索节点。当下一步没有别的任务指派给无人机时,将使用搜索节点,当所有任务都被执行或者没有指派其他的任务时,将到达搜索节点。实际上,当一个无人机到达搜索节点时,它将执行对作战区域的搜索任务。

2.1 决策变量

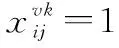
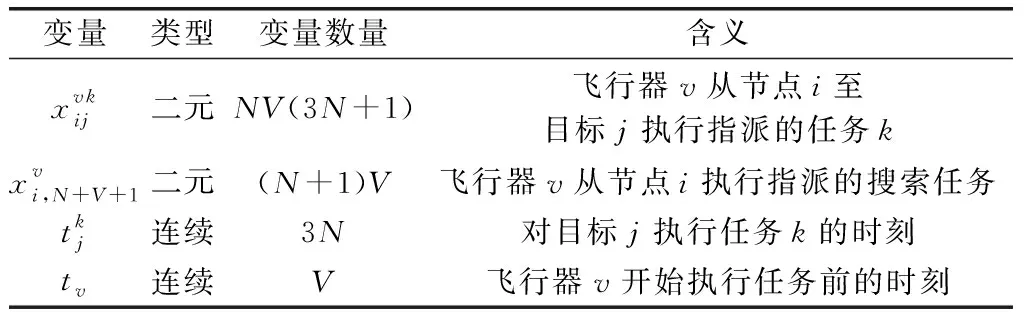
表1 MILP决策变量

2.2 目标函数

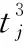
≤tf,j=1,2,…,N

(1)

代价函数是对所有目标执行完任务的总时间最小化,然而,只要对最后一个目标执行任务时没有延迟,该代价函数就不会对单个目标执行任务时产生的延迟进行补偿。因此,为提高性能,可以增加一个小的权重,以激励对每个单独目标也尽快执行完任务。这样,代价函数变为

(2)

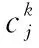
2.3 约束条件

将MILP模型应用于异构无人机任务分配问题的最大难点是把约束条件转化为合理的数学表达式。实现所期望的飞行器行为需要囊括必要的约束条件。完整的约束条件集合包括非时间约束和时间约束两种:

(1) 对于每个目标,3个任务都只能完成一次:

(3)

和

(4)

(2) 每个目标j的任务k最多只能由一架UAV执行:

≤1,k=1,3

(5)

和

≤1

(6)

(3) 每个UAVv从外部最多访问一次目标节点j:

≤1

(7)

(4) 每个UAVv只能进入搜索节点一次:

≤1

(8)

(5) 每个UAVv最多离开节点j最多一次:

≤1

(9)

(6) 由于UAVv执行一次攻击任务之后,就不能再使用了,这样,每个UAVv最多只能攻击一个目标。UAV最多进入目标j一次,因此它不能攻击目标节点j再离开该节点:

≤1

(10)

和

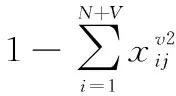
(11)

(7) 如果UAVv对目标节点j执行分类任务,则该无人机必须离开目标节点或者对目标节点j执行攻击任务:

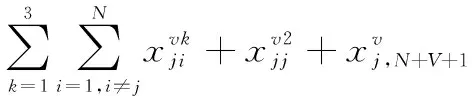
(12)

(8) 所有的UAV必须离开它们的源节点,即使是被指派直接飞往搜索节点:

(13)

(9) UAVv不能离开尚未指派进入的节点j:

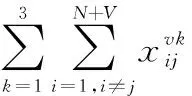
(14)

(10) 一个UAV不能从节点j出来再攻击目标j,除非它进入节点j的目的是执行分类任务:

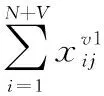
(15)

对于式(1)～式(11),其中i=1,2,…,N+V;j=1,2,…,N;v=1,2,…,V;k=1,2,…,K。

(11) 对于时间约束的线性关系表示可以采用一系列的线性不等式约束。令

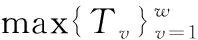
(16)

为所有飞行器中最长的剩余飞行时间。这样线性时间约束可以表示为

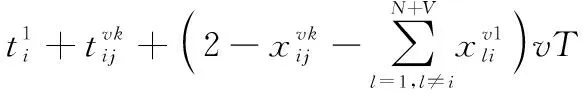
(17)

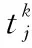
(18)

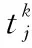
(19)

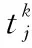
(20)

式中,i=1,2,…,N;j=1,2,…,N;i≠j;v=1,2,…,V;k=1,3。

(12)另外对于飞行器v对目标j既执行分类任务又执行攻击任务的情况,还需要另外的线性时间约束:

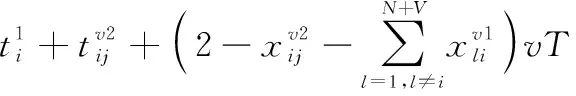
(21)

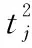
(22)

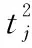
(23)

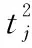
(24)

式中,i=1,2,…,N;j=1,2,…,N;i≠j;v=1,2,…,V。

(13) 每个UAV执行的第一个任务,其约束如下:

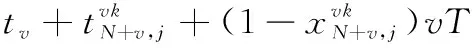
(25)

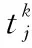
(26)

式中,i=1,2,…,N;v=1,2,…,V;k=1,2,3。

(14)任务优先级次序必须满足:

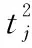
(27)

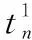
(28)

(15)在同一个目标上的两个相邻任务(如分类和攻击任务,攻击和毁伤评估任务)间由于信号延迟或者烟雾干扰等原因,中间需要加入时间延迟间隔α[α1,α2],可有如下约束:

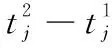
(29)

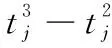
(30)

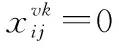
建立了MILP模型后,通过求解约束优化方程,能够得到任务分配结果。

2.4 仿真分析

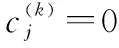
表2 目标任务信息

表3 目标任务执行时间窗

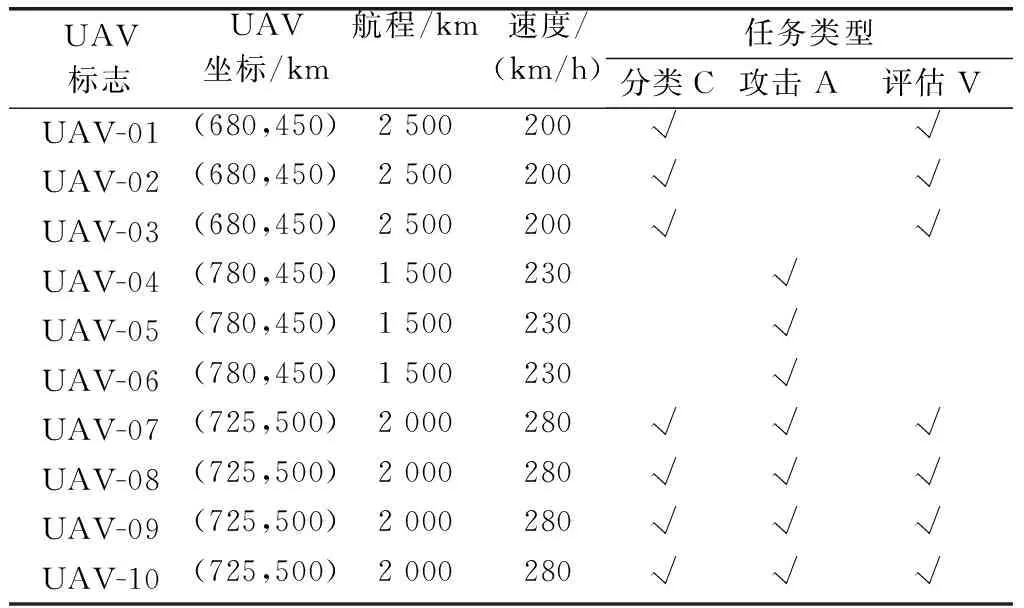
表4 无人机性能参数

对上述MILP问题利用LINGO软件求解,用时为30 min,求解结果如下:

(1) 决策变量

其余为0;

(2) 搜索任务决策变量

其余为0。

(3) 连续时间变量:任务出发时刻(min)

t1=44.7,t2=38.7,t3=33.4,

t7=19.1,t8=22.4,t9=31.8,t10=29.2

其余UAV出发时间为任务开始时刻。

(4) 目标任务结束时刻(min)

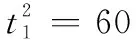
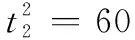
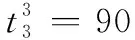
上述任务分配结果如图1所示。

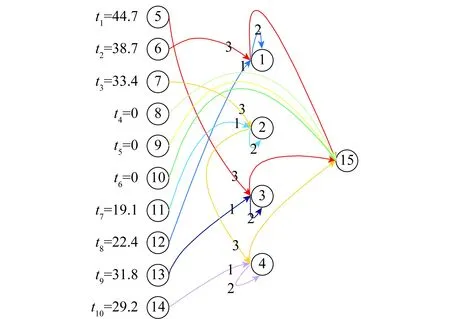
图1 MILP最优任务分配结果Fig.1 Optimal task assignment of MILP

图1表示的任务分配为10架异构无人机编队4个目标时的最优任务分配: UAV-01和UAV-02分别在任务开始44.7 min和38.7 min后出发,分别经过45.3 min和31.3 min到达目标3和目标1,并对他们执行毁伤评估任务;UAV-03在任务开始33.4 min后出发,经过36.6 min到达目标2执行毁伤评估任务,又经过21.2 min达到目标4执行毁伤评估任务;UAV-04、UAV-05、 UAV-06未分配到任务,故一直呈编队状态执行搜索任务;UAV-07在任务开始19.1 min后出发,经过32.6 min到达目标2执行分类任务,随后对目标2执行攻击任务,自爆;UAV-08在任务开始19.1 min后出发,经过35.9 min到达目标1执行分类任务,随后对目标1执行攻击任务,自爆;UAV-09在任务开始31.8 min后出发,经过43.2 min到达目标3执行分类任务,随后对目标3执行攻击任务,自爆;UAV-10在任务开始29.2 min后出发,经过45.8 min到达目标4执行分类任务,随后对目标3执行攻击任务,自爆。

3 基于时间窗的多层编码遗传算法

3.1 算法描述

为避免前述MILP模型优化方法的复杂性,并加快一个良好可行方案的收敛速度,可以采用遗传算法。该类方法不需要计算问题的梯度,可以并行运算,且不会陷入局部极小点,但也可能得不到最优方案。

基于时间窗的多层编码遗传算法中染色体的编码是求解过程中的一个主要工作,染色体可以充分表达简单问题的潜在解;然而,对于较复杂的多目标、多约束优化求解问题,染色体则难以充分表达问题的解。为了解决这个问题,我们改进了编码方式,提出了多层编码遗传算法,把染色体编码从一层拓展为多层,每层编码表达一个或多个约束关系,多层编码共同表达了问题的完整解。

本文染色体编码方式为整数编码,每个染色体个体映射为目标的执行顺序和无人机编号。针对本文的问题,我们取染色体为二层编码,当目标总数为n,每个目标需要执行k项任务,则染色体的长度为2×n×k。其中,第一层染色体编码表示所有目标的执行顺序,第二层编码表示执行上层对应位置对应的任务的无人机编号。以如下个体为例:

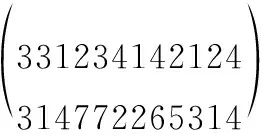
解码后任务顺序表示为:301 302 101 201 303 401 102 402 202 103 203 403。以301为例,其中3表示目标编号,01表示任务编号。从中可以看出,染色体的长度为12×2,任务分配结果如下:UAV-01首先攻击目标3,然后对目标2进行毁伤评估;UAV-02对目标4执行分类任务,然后再以自爆自毁的方式攻击目标1;UAV-03和UAV-04分别对目标3和目标1执行分类任务,然后再执行毁伤评估任务;UAV-05和UAV-06都以自爆自毁的方式对分别目标2和目标4执行打击任务;UAV-07对目标2执行分类任务后,对目标3执行毁伤评估任务。

在无人机任务规划过程中,通常有某个任务要求必须在某个指定的时间范围内完成,则该时间范围就称为时间窗约束。异构无人机编队在反雷达作战中,对敌方雷达站执行打击任务时,打击时间设定在雷达的开机时间[t,t+Δt1]窗口内,对于打击效果的毁伤评估任务为了避免烟尘等影响,需要在打击任务结束后的Δt2时间内进行,超过这两个时间窗口限制,目标状态将发送改变,导致任务效能降低。

3.2 算法流程

基于时间窗的多层编码遗传算法流程描述如下。

步骤1初始化参数

种群初始化,确定初始种群规模、选择概率、交叉概率、变异概率、最大进化代数。

步骤2个体编码

根据打击任务的时间窗口推算分类任务和毁伤评估任务的执行时间,对不符合任务时间窗要求的染色体进行修复,生成合适的染色体进行后续步骤,可以提高算法的计算速度,染色体适应度值的计算根据式(2)给出。

步骤3选择操作

采用轮盘赌法,根据选择概率,在原始种群中选择适应度较好的染色体个体保留到下一代种群中,个体选择概率为

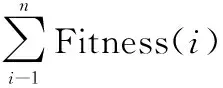
(31)

Fitness(i)=1/Fitness(i)

步骤4交叉操作

根据交叉概率,从种群中选取两个染色体,随机确定染色体上的交叉位置,将两个染色体上层对应交叉位置的基因编码进行交叉操作。操作方法如图2所示。

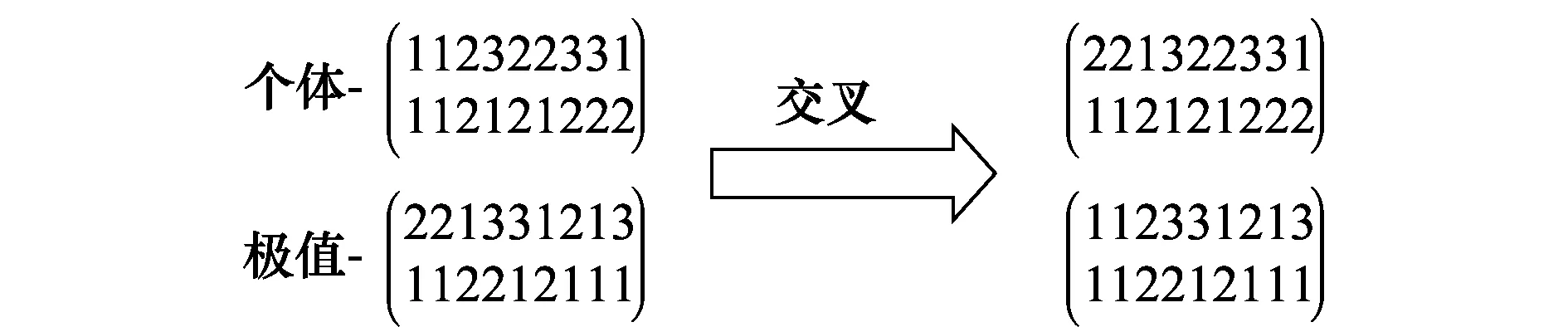
图2 交叉操作Fig.2 Crossover operation

由于将合理染色体的编码顺序交叉后容易出现某些目标的任务多余而某些目标任务缺失,因此需要进行编码的调整和修复:把任务多余的基因位调整为任务缺失的基因,并且按交叉操作之前编码第二层所对应的无人机编号来调整编码,调整操作方法如图3所示。

图3 调整编码Fig.3 Code adjustment

步骤5变异操作

根据变异概率,在种群中随机选择变异个体,随机选择染色体的两个变异位置,把染色体中两个变异位置对应的基因以及下层编码对应的无人机编号进行交换。操作方法如图4所示。

图4 变异操作Fig.4 Mutation operation

步骤6合并父代和经过选择、交叉、变异操作后产生的子代种群,生成混合种群。

步骤7计算混合种群适应度值。

步骤8判断是否满足循环终止条件,若不满足,跳转到步骤2,循环直至满足终止条件,最终输出最优任务分配方案。

3.3 仿真分析

算法的基本参数为:种群数目为50,最大迭代次数为100,选择概率为0.94,交叉概率为0.8,变异概率为0.1。仿真平台与上述相同,求解用时为4.5 s,算法的搜索过程如图5所示,表示随着遗传代数的进化,种群最优解与均值的变化关系。算法在第80代时得到最优解,最优解为92.8 min。

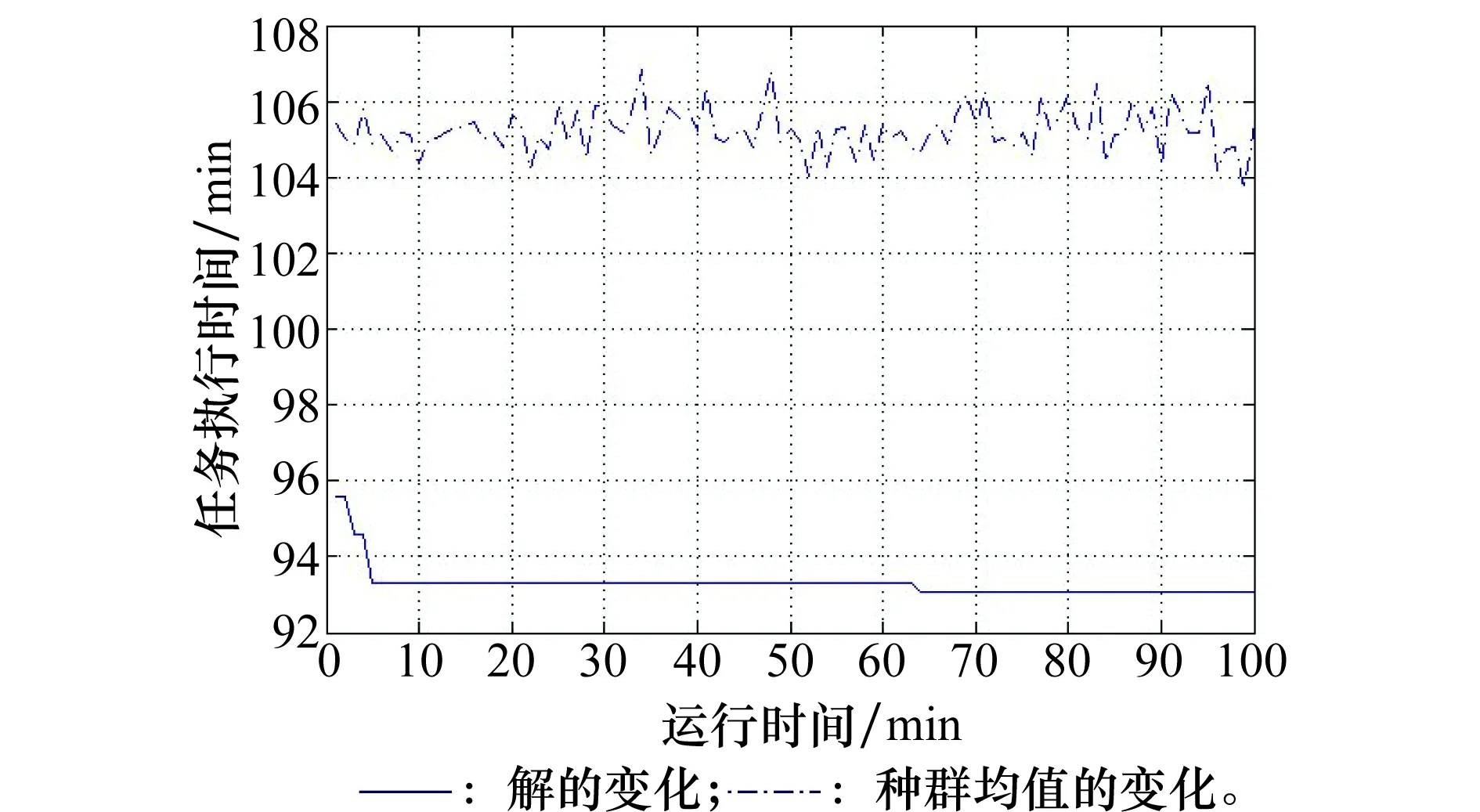
图5 算法搜索过程Fig.5 Algorithm search process

最优个体对应的任务执行顺序甘特图如图6所示。

结果说明: UAV-01在任务时刻出发,经过36.6 min到达目标2执行分类任务,在43.5 min时刻开始经过30 min至目标1执行毁伤评估任务;UAV-02在任务开始51.6 min后出发,经过36.6 min到达目标2执行毁伤评估任务;UAV-03未分配到任务,故一直呈编队状态执行搜索任务;UAV-04在任务开始40.9 min后出发,经过39.5 min到达目标4执行攻击任务,自爆;UAV-05未分配到任务,故一直呈编队状态执行搜索任务;UAV-06在任务开始19.9 min后出发,经过42.8 min到达目标1执行攻击任务,自爆;UAV-07在任务开始49.6 min后出发,经过43.2 min到达目标3执行毁伤评估任务;UAV-08在任务时刻出发,经过45.8 min到达目标4执行分类任务,在53 min时刻开始经过21.2 min至目标2执行攻击任务,自爆;UAV-09在任务开始38.3 min后出发,经过43.2 min到达目标3执行攻击任务,自爆;UAV-10在任务开始时刻出发,经过35.9 min到达目标1执行分类任务,而后经过21.2 min到达目标3执行分类任务,在60.9 min时刻开始经过30 min对目标4执行毁伤评估任务。

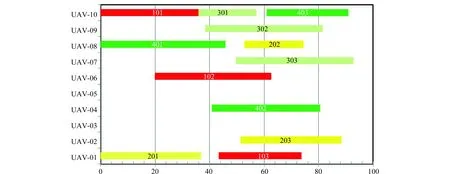
图6 任务执行甘特图Fig.6 Task execution Gantt chart

4 对比与分析

本文利用MILP和基于时间窗的多层编码遗传算法解决异构无人机编队在反雷达作战中的协同任务分配问题,仿真结果表明二者都能得出可行最优分配方案及任务执行时序图。对比发现:①在相同的平台下,基于时间窗的多层编码遗传算法的求解时间远快于MILP方法;②MILP方法得到任务执行最短时间为91.2 min,而基于时间窗的多层编码遗传算法得到的最短执行时间为92.8 min。经过分析,由于MILP方法通过搜索得到的是目标函数的全局最优解,故其精度更高。

仿真分析表明,MILP模型通过数学表达式可以方便地将时间、空间、物理、逻辑约束联系起来,将一个实际的作战任务转化成数学问题,能够求解有时间窗要求的任务分配问题。但用数学表达式将所有的约束问题融入到一个MILP模型中,将导致NP-Hard优化问题,且计算量随着求解规模呈指数递增。以本次仿真采用的计算平台为例,一般地,对于规模大于2个目标,且每个目标有3个任务的问题,难以实现实时求解。鉴于MILP在分配最优性方面的优势,对于中等规模的问题,可以采用MILP离线方式寻找到最优分配方案。

基于时间窗的多层编码遗传算法亦可以得到异构无人机编队任务分配方案,便于利用甘特图直观表示任务执行时序,其显著特点是算法执行时间大大小于MILP方法。在算法中,编码是迭代处理的前提,染色体编码难以精确体现所有约束,因此求解方案的最优性将会受到一些影响,但仍可以得到可行的任务分配结果。

概括来讲,基于MILP的任务分配能够得到全局最优解,但当问题规模较大时难以满足实时性,适用于小规模任务分配实时解算;基于时间窗的多层编码遗传算法具有明确的计算优势,但可能得到局部最优解,适用于为较大规模任务分解实时提供初始任务分配方案。

5 结 论

本文利用MILP和基于时间窗的多层编码遗传算法解决异构无人机编队在反雷达作战中的协同任务分配的问题。MILP模型将实际作战任务转化成数学规划问题,简明易懂,对于小规模的问题可以在线运行得出最优的分配方案。相对于MILP模型,基于时间窗的多层编码遗传算法计算效率高,通过能够实时给出良好的分配方案,在异构无人机编队任务分配中,可根据任务分配规模、用户需求选择使用两类算法。