有风攻角的棱柱体驰振计算方法研究

谢兰博， 廖海黎

(1.中铁大桥勘测设计院集团有限公司，武汉 430050； 2.西南交通大学 风工程试验研究中心，成都 610036)

横风向驰振是一种发生在细长结构上较常见的气动发散性振动。原因是在一定风速下气动力对结构的气动阻尼为负并大于结构阻尼，对结构做正功，使得结构振动振幅逐渐变大，而随着振幅的逐渐增大，气动负阻尼降低，有可能和结构阻尼达到平衡，使得结构振动振幅达到稳定。驰振的振幅较大，往往达到数倍以至于十几倍横风向尺寸。而且振动频率往往较小，一般远小于相同截面的漩涡脱落频率[1]。

气动发散振动的振幅计算一般认为开始于Parkinson，他将升力系数表达为关于风攻角的多项式形式，代入振动方程，利用渐进法求出了方程的近似解析解，发现和试验吻合的非常好[2-3]。随后，Novak等[4-6]探讨了紊流对驰振的影响，Lanevile[7]对这方面有非常详细的阐述。Blevins[8]分析了多自由度的情况。关于驰振的振型展开，Novak[9]和Sullivan[10]都做过详细的工作，而且又以Sullivan最具有代表性。

驰振相关的计算理论基本上都来源于Parkinson，他的基本思路如下。

当来流风和振动方向垂直时，将升力系数表达为风攻角的奇数次多项式形式，简记为

Fv=f(α)=c1α+c3α3+c5α5+…

(1)

那么振动方程可以写为

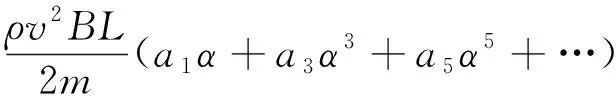
(2)

式中：ξ为结构阻尼比；ω为结构自振圆频率；ρ为空气密度；B为特征尺寸；m为结构质量；vr为等效风速；v为来流风速。

令μ=0.5(ρv2BL)/m，则振动方程为

(3)

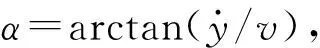
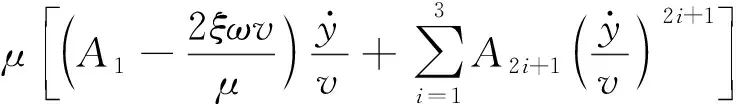
(4)

令

(5)

则式(4)可以进行参数无量纲化

Y″+Y=ηf(Y′)=

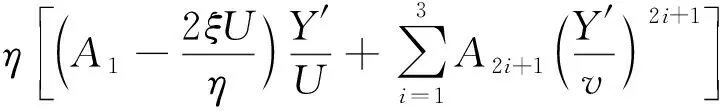
(6)

上式等号右边线性项为0时，即是驰振振动发散的临界状态，经过化简即可得到Den-Hartog公式。当线性项大于0时，驰振振动发散。一般情况下ηA1远小于1，式(6)满足弱非线性条件，可以求得近似解析解。根据非线性振动理论，有如下等式近似成立

(7)

式中：a是驰振振幅。实际工程中，我们更关注的是稳定后的振幅大小，令等式两边为0，可得

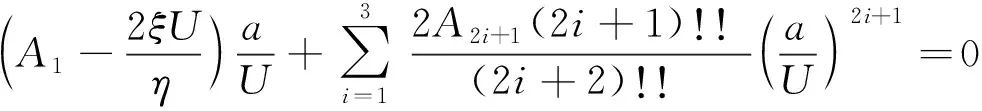
(8)

求解式(8)即可得到稳定的振动振幅，事实上求得风速位移曲线也就得到了临界风速。

驰振的理论计算主要包括预测临界风速和计算驰振振幅，关于前者现在通用的依然是Den-Hartog公式，但是Den-Hartog公式严格来说仅仅适合0°攻角，即振动方向和来流风垂直，而对于非零攻角只是一种近似。国内大都直接利用Den-Hartog公式计算振动方向和来流方向不垂直的驰振临界风速，关于两者的差别，本文后续将做详细的讨论。关于驰振的振幅计算，国内外研究也主要集中在0°攻角的情况，对于非零攻角情况大都是一些试验研究[11]，还未有理论计算出现。本文首先推导了振动方向和来流风不垂直的驰振计算方法，然后利用H形截面模型开展实验，发现理论计算和试验结果吻合的比较好，证明了本文计算方法的可靠性。

1 驰振临界风速的计算

如图1所示，结构有x和y两个振动主轴，驰振一般放生在风攻角为0°附近或者90°附近，当风攻角较小，在0°附近时，结构驰振振动为y方向；当风攻角较大，在90°附近时，结构驰振振动为x方向，且振动方向都和模型主轴垂直，这两种情况研究方法一致，因此本文选用风攻角在0°附近的情况，即振动为y方向。结构的风攻角为α0，振动方向来流风速为v，振动方向向上为正，位移为y，则根据几何关系可得等效风攻角α满足

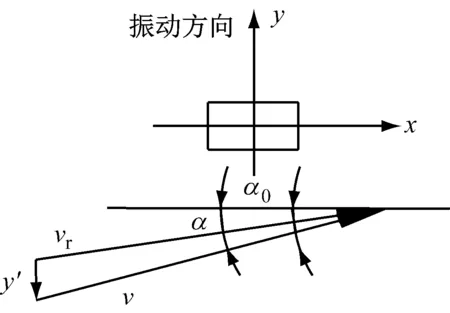
图1 有风攻角的驰振计算Fig.1 Calculation of galloping vibration with wind attack angle

(9)

等效风速vr满足

(10)

根据式(10)可得

(11)

结构振动方程可以写成

(12)

式中：Cv是体轴下升力系数；ξ是阻尼比；ω是振动圆频率；m为模型质量；ρ是空气密度，；本文中取1.225 kg/m3；B是特征尺寸；L为模型长度。

将式(9)和式(11)代入式(12)，可得

(13)

(14)

则可以得到体轴下的升力系数为

(15)

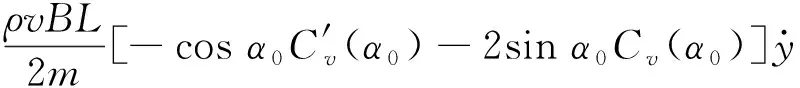
(16)

观察式(16)，当等式两边阻尼相等时是驰振发散的临界点，即可得临界风速为

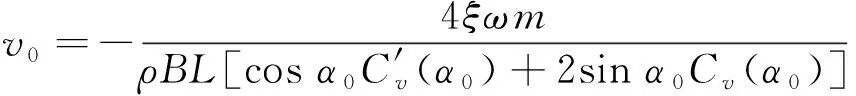
(17)

上述推导都是基于体轴坐标系，而风轴坐标系下的推导思路和上述一致，即升力为

Fv=

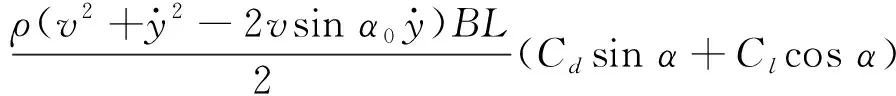
(18)

将其按照一次多项式展开，并去掉常数项，可得

(19)

根据式(19)，可以得到驰振临界风速为

v0=

(20)

观察式(20)，当风攻角为0时，就可以退化为Den-Hartog公式。从以上推导可以看出，Den-Hartog公式严格说仅适用于振动方向和来流风垂直的情况，对于0°攻角是一种近似。

2 驰振振幅的计算

根据式(13)，可以得到当风攻角为α0时振动方程为

(21)

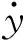
观察等效风攻角和振动速度的关系，牵涉反正切计算，因此本文将升力系数表达为风攻角正切值的多项式形式，以方便公式推导。和Parkinson一致，本文也取到七次多项式，即

(22)

结合式(21)，可得升力表达式为

(23)

联立式(22)和式(23)，将升力系数展开，去掉偶次幂，保留到7次幂，可得升力表达式为

(24)

其中：

c7A0=c6s(c1-c3+c5-c7)+c4s(c3-2c5+3c7)+

c2s(c5-3c7)+sc7，

c7A1=c8(2c1-2c3+2c5-2c7)+c6(-3c1+7c3-

11c5+15c7)+c4(-5c3+16c5-33c7)+

c2(29c7-7c5)-9c7，

c7A3=c6(-c1+9c3-25c5+49c7)+c4(-10c3+

60c5-182c7)+c2(217c7-35c5)-84c7，

c7A5=c4(-c3+20c5-105c7)+c2(231c7-

21c5)-126c7，

c7A7=c2(35c7-c5)-36c7，

c=cosα0,s=sinα0

(25)

由于常数项只是产生一个不变动的位移，所以可以删去，令

(26)

则振动方程可以写为

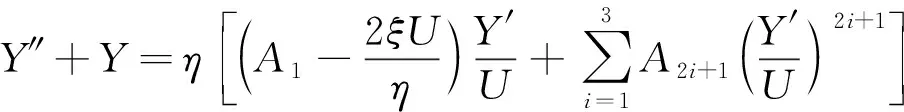
(27)

假定结构驰振时振动为简谐振动，振幅保持不变，且振动频率和0风速时保持一致，即

Y=asinτ,Y′=acosτ

(28)

则可以得到当驰振发生时，在振动一个周期阻尼力和气动力做功为

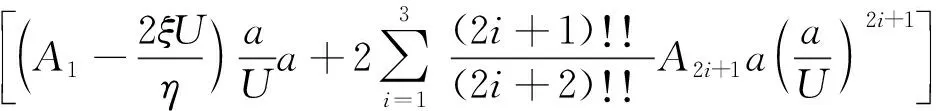
(29)

令振幅的平方为x，即：a2=x，则可得

T(x)=mh2ω2η×

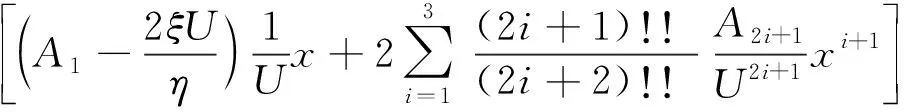
(30)

驰振达到稳定的振幅时一个周期内外力做功是0，所以令式(30)两端为0，就可以求出振动稳定时的振幅。整理可得振幅满足如下方程

B1x+B3x2+B5x3+B7x4=0，

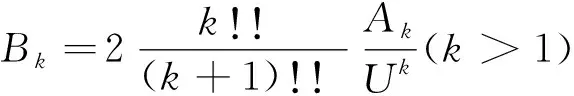
(31)

令

(32)

则消去方程的二次项，式(31)可以转化为如下形式

z3-αz-β=0

(33)

参考恒等式

(m+n)3-3mn(m+n)-(n3+m3)=0

(34)

可得

α=3mn，

β=n3+m3

(35)

所以m+n即是式(33)的一个根，根据韦达定理可以求出另外两个根。

根据以上推导，可得式(31)有三个根如下所示

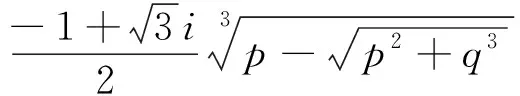
(36)

其中

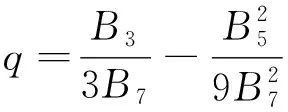
(37)

因为p和q是实数，所以x1肯定是实数。观察x3和x2的形式，可以看出如果三次开方下是虚数的话，则x3和x2的虚数部分正好可以抵消掉，也就是p2+q3<0时，三个根全部都是实数，而且各不相等；p2+q3>0时，方程有一个实数根和一对共轭复数根；p2+q3=0时方程有一个实根和一对相等的实根，其中如果p=0，q=0，方程有三重根。

如果仅在数学上考虑式(30)，求其振幅本质上是研究其极循环。根据近似解析解可以证明其最多有三个极循环，其实在实数域上他最多有三个，而到复数域上，他一定是有三个极循环。此处采用七次多项式是因为他最多可能有三个极循环，而只有两个稳定，这和试验比较吻合；如果采用五次多项式，则在实数域上他最多有两个极循环，其中还有一个不稳定；如果采用三次多项式，则极循环个数就会降到一个。因为根据实测竖向驰振最多有两个稳定的极循环，因此采用七次多项式拟合是比较合理的。

驰振达到稳定的振幅时一个周期内外力做功必然是0，但是外力做功是0并不一定能达到稳定的驰振状态。只有当振幅稍微增大外力做功为负，振幅稍微减小而外力做功为正时，这个振幅才是稳定的振幅，否则这个振幅只能说理论上存在而已。这个条件可以表达为

(38)

只要能满足式(38)，就可以认为xi是稳定的振幅，否则就不是稳定振幅。

以上计算方法可以求得驰振稳定的振幅，但是不能求解驰振振幅逐渐增大的过程，下面给出求解发散过程振动的求解方法。

在振动过程中系统的总能量为

(39)

能量对时间的导数为外力的功率，因此可以得到

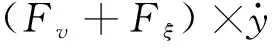
(40)

式中：Fξ代表阻尼力。假定驰振振幅在一个周期内变化不是很大，则将式(40)在一个周期上取平均值，即可得到

(41)

结合式(39)对式(41)进行计算并化简a2=x，则可得

(42)

观察式(42)，当驰振稳定时，振幅保持不变，上式左右都为0，即可得到稳定的振幅。式(42)是常微分方程，求解较复杂，对其分离变量可得

dτ=

(43)

求解式(43)需要先求解出式(31)的三个解，然后分解因式，即可以求出时间关于振幅的函数。

3 工程实例

在我国，大跨度拱桥大量采用H型截面刚性吊杆，如佛山东平大桥的H型吊杆长达40.8 m。相对于圆形截面的平行钢丝或者钢绞线这一类较柔的吊杆，H型截面吊杆的空气动力学性能更差，更容易发生各类风致振动。因此本文选用H型截面模型作为研究对象开展实验。

本文实验在西南交通大学单回流串联双试验段工业风洞(XNJD-1)第二试验段中进行，该试验段断面为2.4 m(宽)×2 m(高)的长方形，最大来流风速为45 m/s，最小来流风速为0.5 m/s。

实验模型截面为H形，高宽比为0.845∶1，模型长度为1 m，竖向为y方向，其尺寸如图2所示。

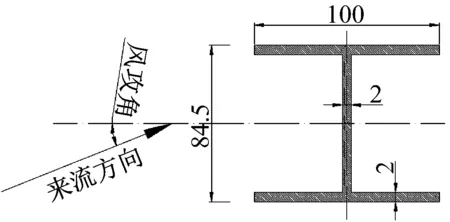
图2 模型截面尺寸(mm)Fig.2 Model section size (mm)

升力和阻力系数定义如下

(44)

式中：U=14.6 m/s，B=0.1 m，L=0.3 m。所测风轴下阻力和升力系数如图3所示。

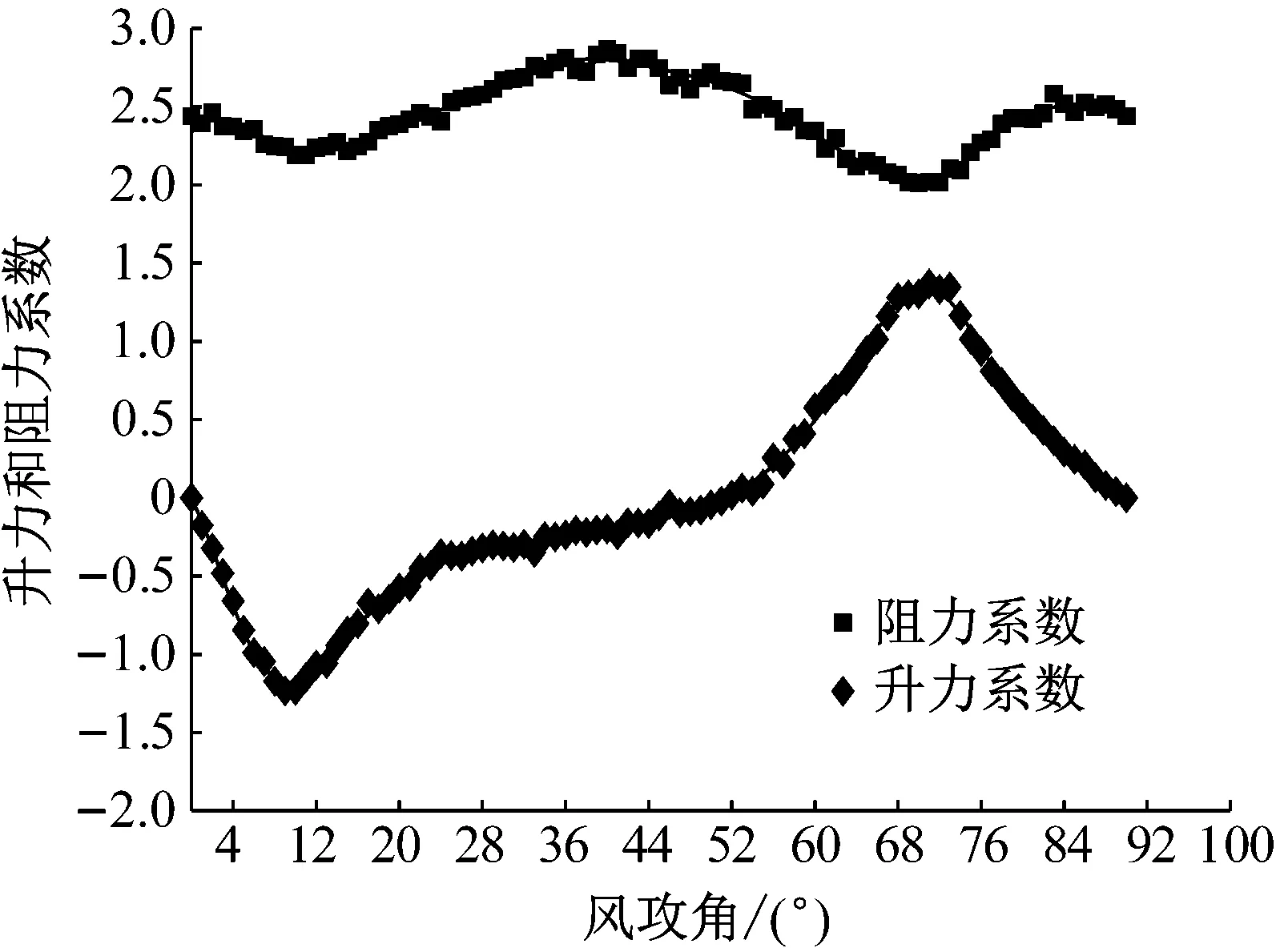
图3 升力和阻力系数Fig.3 Lift and drag coefficient

图3中散点是试验所测结果，而曲线是利用25次多项式拟合所得结果，数据相对较光滑，本文插值计算采用25次多项式拟合的结果。

定义驰振力系数如下所示

Fdsin2α0+Fd

(45)

式(45)中SDe代表的是利用Den-Hartog公式所定义的驰振力系数，Sα是根据本文式(20)所定义的驰振力系数，由于本文推导的临界风速公式振动方向是确定的，而振动结构一般都是有两个主轴，所以式(20)只能代表一个主轴方向，另一个方向的公式需要做一个旋转变换。根据式(45)和本文所测风轴的三分力系数，可得两种定义方法的驰振力系数对比，如图4所示。

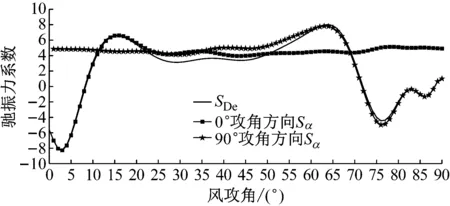
图4 驰振力系数对比Fig.4 Comparison of galloping force coefficient

如图4所示，本文所推导结果和Den-Hartog公式结果在0°攻角和90°攻角附近非常接近，在70°～80°攻角范围内两者误差稍大，而在20°～65°攻角范围内两者则有很大的误差，由于Den-Hartog公式假定振动方向和来流风垂直，因此，在有较大风攻角的临界风速判定建议采用本文所推导公式。观察图4还可以发现，0°攻角附近比90°攻角附近更容易发生驰振，因此本文重点研究0°攻角附近的驰振振幅。

风洞试验对于风攻角设置方面大致有两种思路，第一种是改变模型的倾斜角度，而弹簧依然和来流风垂直；另一种是改变模型和弹簧的倾斜角度，使得能够实现和事实符合的风攻角。第一种情况容易实现，而且在风攻角比较小的情况下，所得结果和实际相差很小，但是在风攻角较大时，所得结果将会和实际产生较大误差。第二种情况实现较麻烦，但是和实际一致，本文实验采用第二种方法。

如图5所示，风攻角设置和实际一致，实验风攻角为0°、6°、8°和20°四个工况。试验模型质量为6.5 kg，y方向振动频率为2.82 Hz，扭转频率为5.4 Hz，y方向振动阻尼比约为0.05%，扭转阻尼比约为2.5%。所测y方向位移曲线如图6所示。

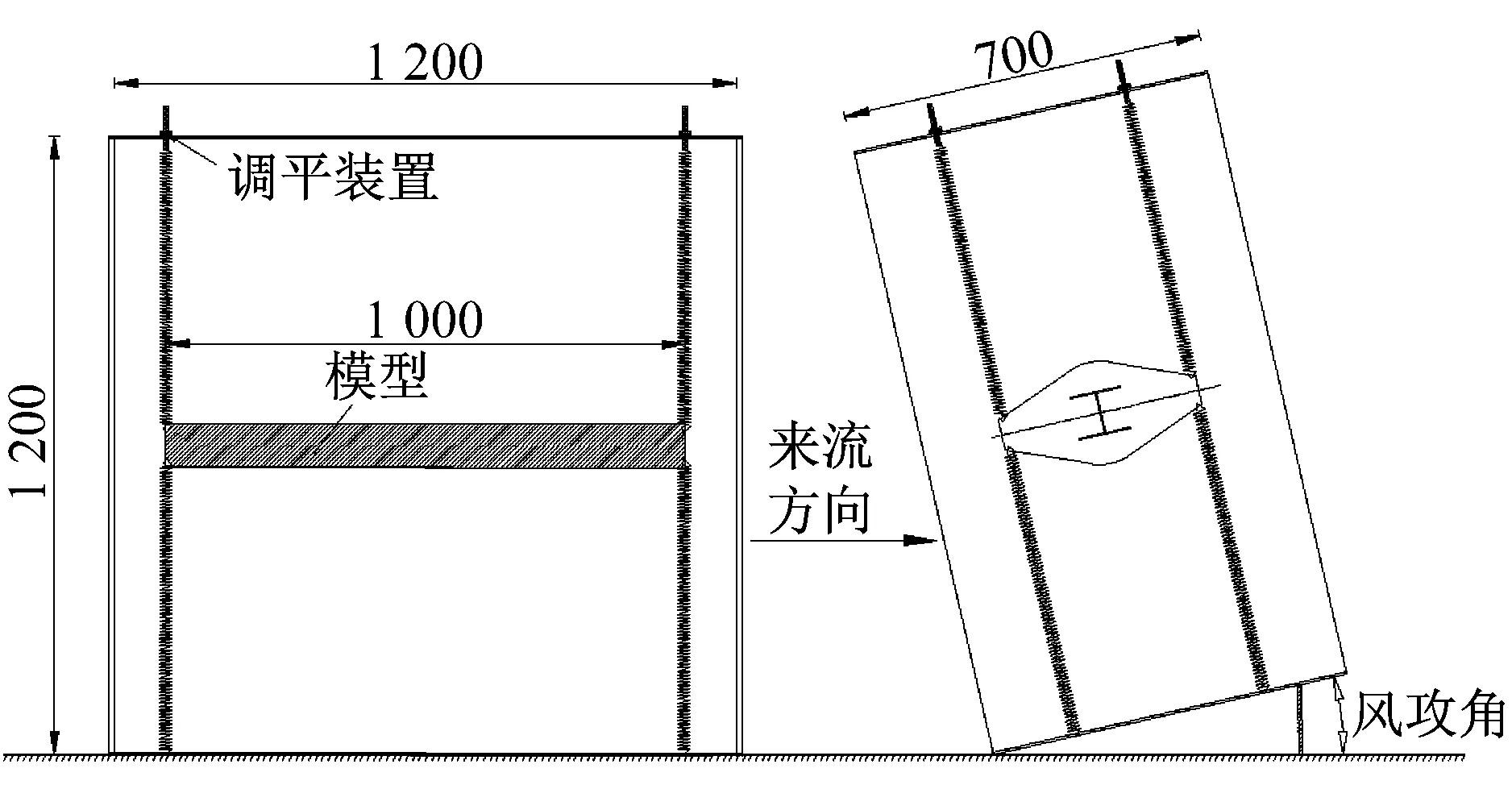
图5 风攻角设置示意图(mm)Fig.5 Schematic plot of wind attack angle (mm)

从图6可知，在0°攻角工况下位移增长最快，攻角越大，增长越慢，而20°攻角情况下，驰振消失。

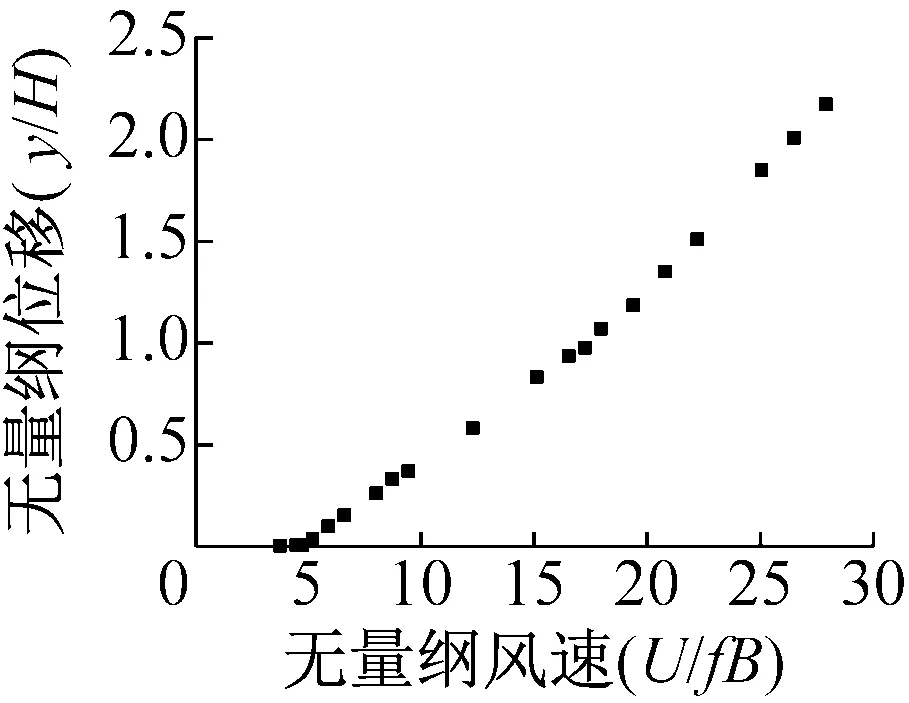
(a) 0°攻角风速位移曲线

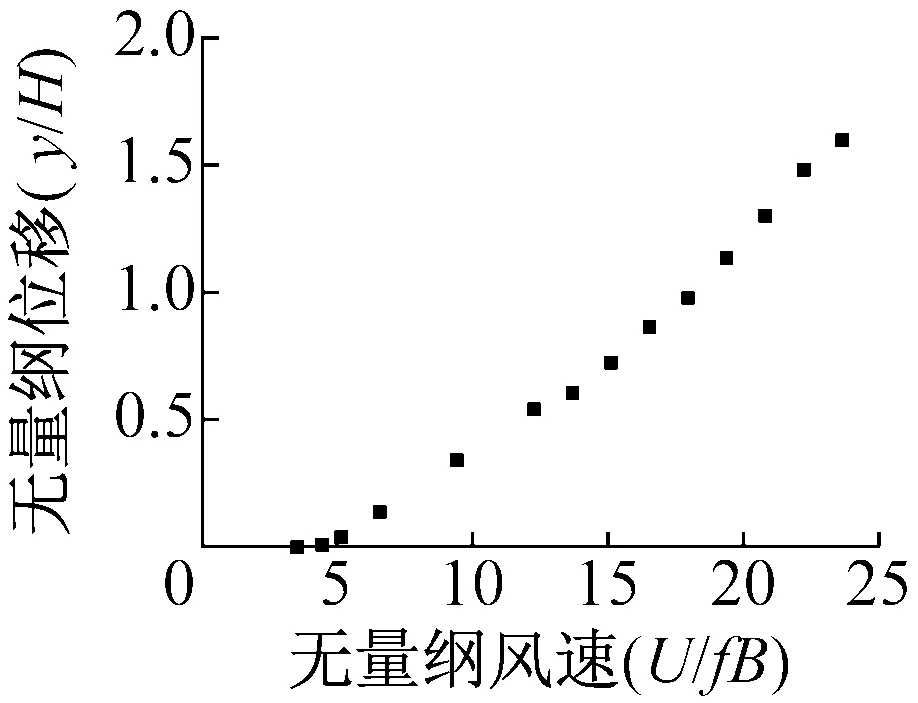
(b) 6°攻角风速位移曲线

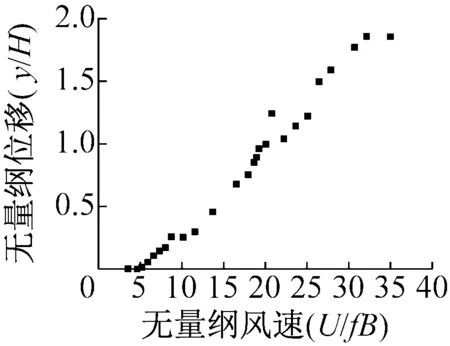
(c) 8°攻角风速位移曲线

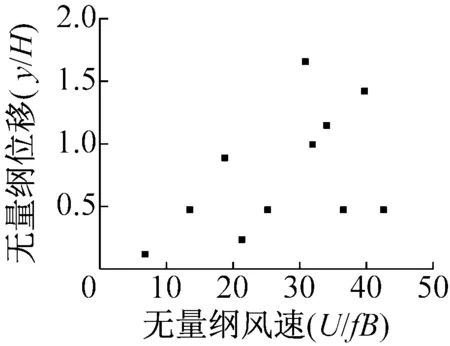
(d) 20°攻角风速位移曲线图6 风速位移关系Fig.6 The relationship between wind speed and displacement

已知结构三分力系数，利用多项式拟合进行计算无论如何拟合数据都会和原数据有一定的差异，所以本节先介绍利用三次样条插值进行升力系数拟合而进行数值计算的求解结果。图7是模型分别在0°、6°和8°攻角下的理论计算和实验的对比。因为20°攻角未发现驰振现象，所以在此不做讨论。

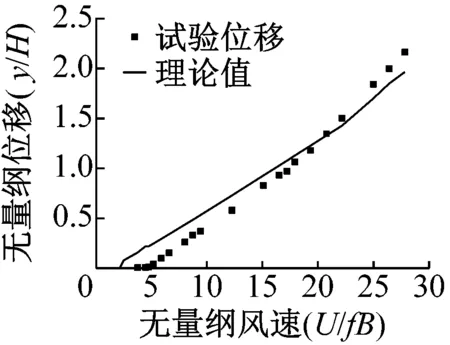
(a) 0°攻角试验和理论驰振振幅对比

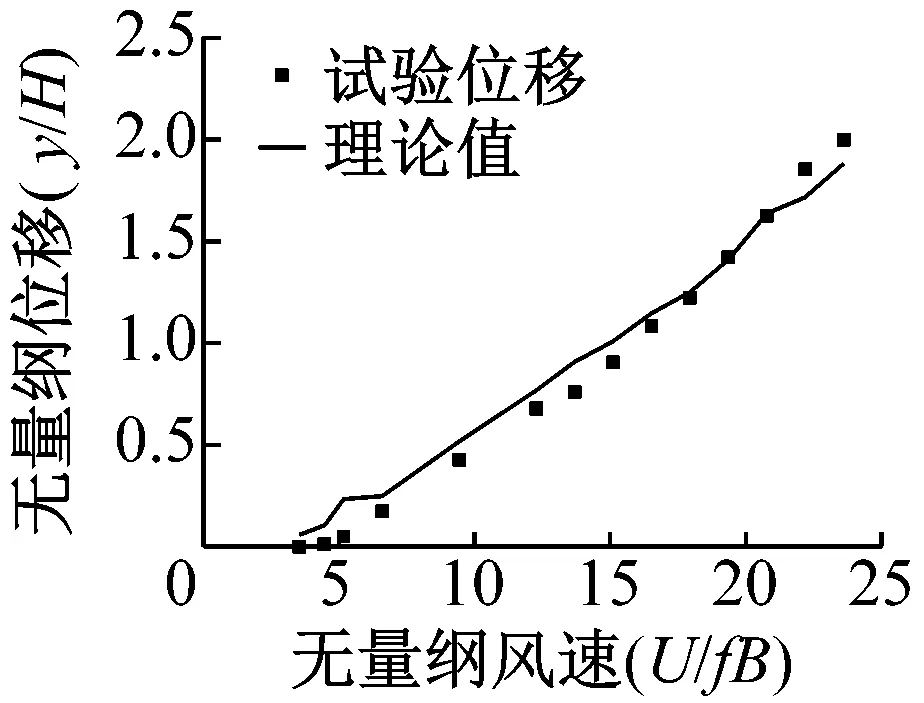
(b) 6°攻角试验和理论驰振振幅对比

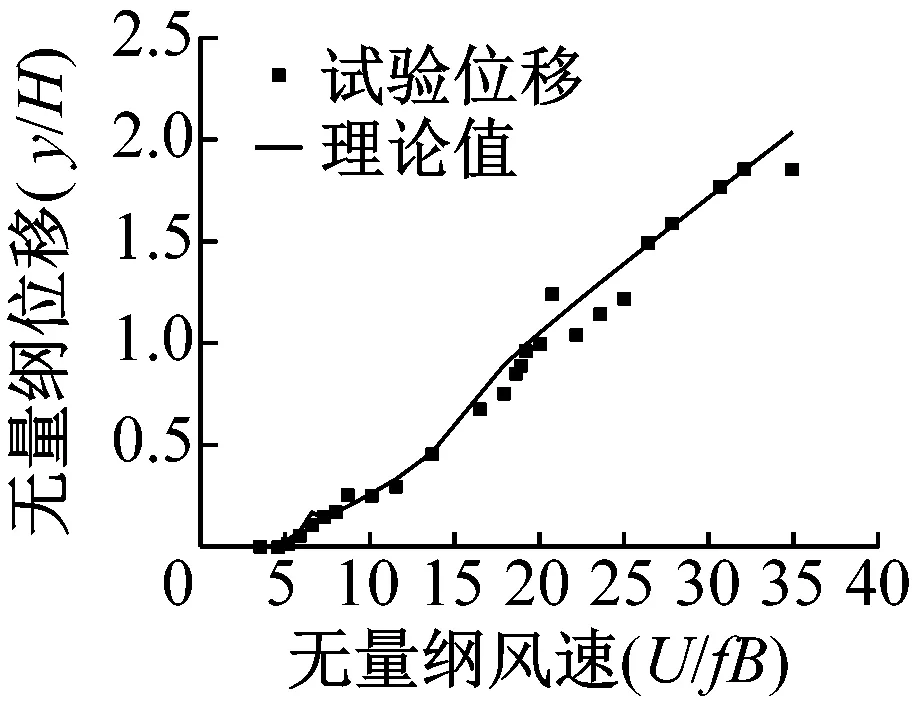
(c) 8°攻角试验和理论驰振振幅对比图7 试验和理论驰振振幅对比Fig.7 Experimental and theoretical comparison of the amplitude

由图7可知，8°攻角位移曲线和试验吻合非常好，其次是6°攻角，而0°攻角理论计算和试验所测位移有一定的偏离。但是三者在较高的风速时，理论计算和实验都趋向于一致，说明在高风速下准定常理论成立的较好。这说明了本文所推导有风攻角计算驰振的公式的正确性。在低风速时，0°攻角和6°攻角计算和理论偏移较大，甚至0°攻角计算的临界风速和实验值相差到了40%～50%，产生以上误差的原因可能是：

(1)准定常理论的局限性。准定常理论本身就会有一定的误差，气动力总会存在滞后现象。

(2)涡激力的影响。如果在驰振的风速下漩涡脱落频率和结构振动频率接近，则会导致试验振幅和计算的结果偏离很远。本实验驰振临界风速非常低，只有1.5 m/s左右，为了弄清楚涡激力对驰振的影响，需要计算出结构的斯托罗哈数。本文借助Fluent软件利用CFD进行数值模拟，求取结构的斯托罗哈数。网格划分如图8所示。

边界条件设置为：上游速度入口，使用Velocity-inlet边界条件，湍流模型采用SSTk-ω，湍流强度取0.2%，湍流黏性比取10%，下游使用pressure-outlet边界条件，出口相对压强平均值取0，上下侧边界条件是Symmetry边界条件，H形截面的表面采用No-Slip Wall边界条件。

图8 网格划分Fig.8 Mesh partition

求解设置为：静力计算压力-速度耦合算法使用PISO算法，离散格式控制方程采用QUICK格式进行求解，计算时间步长0.005 s。采用Interface边界利用滑移网格方便旋转模型，求得结果如表1所示。

观察表1可以看出，对于0°攻角，St≈0.13，当振动频率为2.82 Hz时，对应涡激共振风速为2.16 m/s，而这个风速恰好是0°攻角驰振刚发生不久，同理计算出6°攻角及8°攻角对应涡激共振风速分别为1.96 m/s和1.86 m/s，都是对应驰振发散刚刚发生，所以有可能涡激力影响了理论计算和实验结果之间的差别。

利用样条插值计算驰振位移虽然比多项式拟合更精确，但是它不能写出解析形式，因此其应用有一定的局限性。图9是利用七次多项式进行升力系数拟合结果。

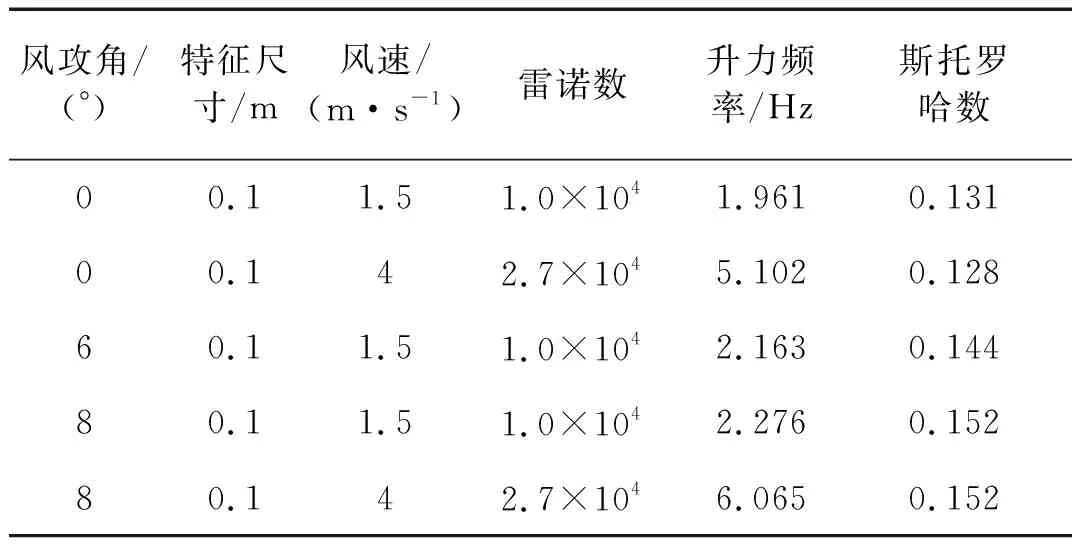
表1 斯托罗哈数计算结果Tab.1 Results of calculation of Strouhal number

利用最小二乘法，可得升力表达式为

Cv=c1tanα+c3tan3α+c5tan5α+c7tan7α

(46)

式中：c1=-7.6，c3=131.8，c5=-635.9，c7=1 016.9，代入到式(25)，求出各攻角之下各风速之下的振幅，并用式(38)判断是不是稳定的振幅。利用多项式求得驰振振幅如图10所示。

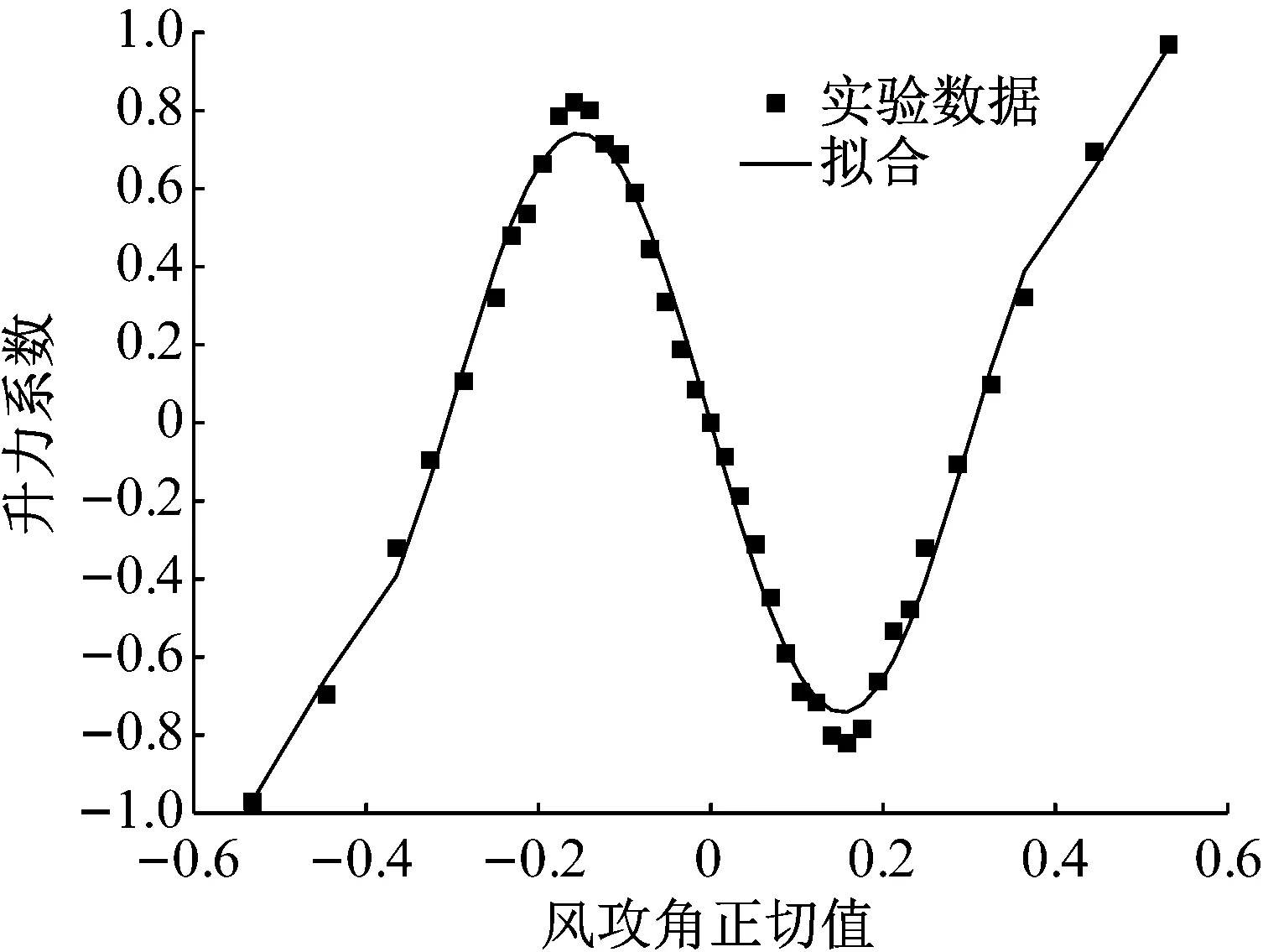
图9 多项式拟合升力系数结果Fig.9 Polynomial fitting lift coefficient results

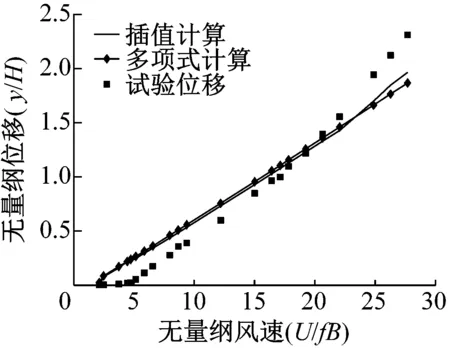
(a) 0°攻角驰振振幅试验和理论对比

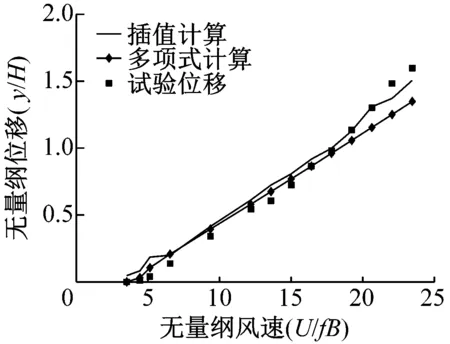
(b) 6°攻角驰振振幅试验和理论对比

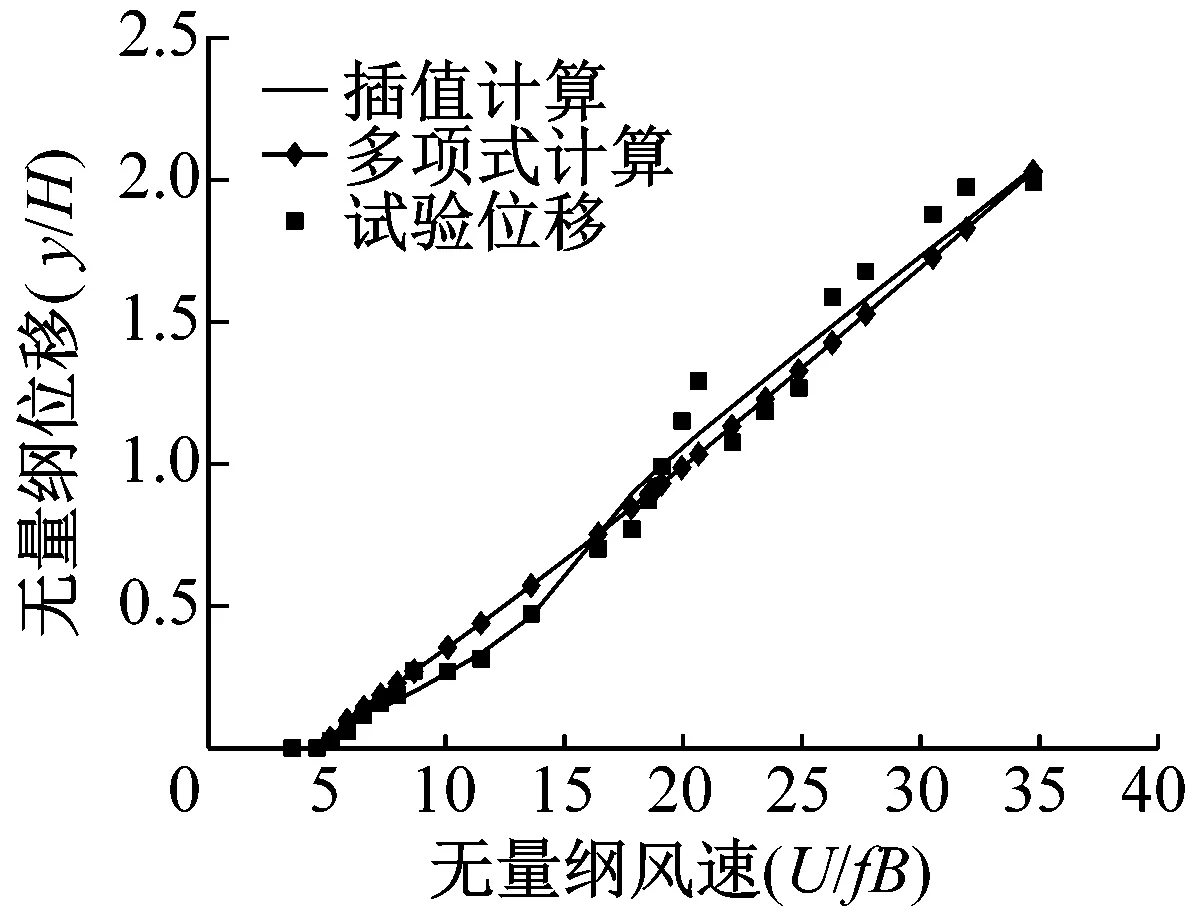
(c) 8°攻角驰振振幅试验和理论对比图10 驰振振幅试验和理论对比Fig.10 Experimental and theoretical comparison of the amplitude

观察图10，可以看出多项式拟合和插值计算结果比较接近，这是因为升力多项式拟合结果和原来的数据误差很小。

4 结 论

本文推导了有风攻角的驰振临界风速和振幅计算公式，利用Den-Hartog公式求解临界风速和本文公式对比，并采用H形截面模型开展实验对振幅加以验证，讨论了理论计算和试验产生误差的原因，有以下结论：

(1)Den-Hartog公式并不适用于来流风和振动方向夹角较大的情况，通过和本文公式对比，认为在较小的风攻角之下，Den-Hartog公式误差不大，但是较大的风攻角，Den-Hartog公式计算结果会慢慢偏离本文所推导的公式计算结果，因此建议对于有风攻角的驰振计算应采用本文所推导公式。

(2)本文所推导的有风攻角驰振振幅计算公式计算结果和试验结果较为吻合，证实了本文所推导计算公式的正确性。