基于概率序列的含风光电力系统可靠性评估方法
高 博,王小明,谢毓广
(国网安徽省电力有限公司电力科学研究院,安徽 合肥 230601)
0 引言
研究含间歇性能源的电力系统可靠性常用的方法是蒙特卡罗模拟法[1]。蒙特卡罗方法便于处理随机特性,得出的结果精度较高,但是仿真所需的时间代价相对较大。在含有间歇性能源的电力系统规划阶段,常常需要对多个方案进行优选比较而进行供电可靠性评估。这类评估的精确度要求不是很高,时间代价不能太大,而且涉及网架结构的调整。因此,在这种应用背景下常规的蒙特卡罗方法显得效率较低。
本文提出一种基于生产模拟概率序列的含风光电力系统可靠性评估方法。首先,利用威布尔(Weibull)分布与贝塔(Beta)分布描述一个地区风速与太阳辐照度的概率分布特性;然后,建立合适的风电、光伏及负荷的并网模型;最后,选取停电概率(LOLP)和停电电量期望值(EENS)作为可靠性评估指标,基于生产模拟概率序列理论,对含风光系统的可靠性指标进行计算评估。在MATLAB中编程对IEEE RBTS BUS6系统进行仿真计算,结果表明上述方法相对于蒙特卡罗方法,能够在保证计算精度的同时,显著缩小计算的时间代价。
1 风电场与光伏电站并网模型
1.1 风速与太阳辐照度概率分布模型
采用双参数的Weibull分布描述风速的概率密度[2~3],其概率密度函数为:
(1)
式中:v为风速;k,c分别为Weibull分布形状参数和尺度参数。
采用Beta分布[3]描述短时间内(几个小时)太阳光照强度的概率分布特性,其概率密度方程为:
(2)
式中:Γ(·)为伽马函数;r为实际光照强度;rmax为最大光照强度;α、β为贝塔分布形状参数。
α、β的计算方法为:
(3)
(4)
式中μ和σ2为一段时间内光照强度统计数据的平均值和方差。不同季节、不同天气的α、β取值不同。
1.2 风电场并网模型
风力发电机的出力与风速紧密相关,二者之间的关系如图1所示。
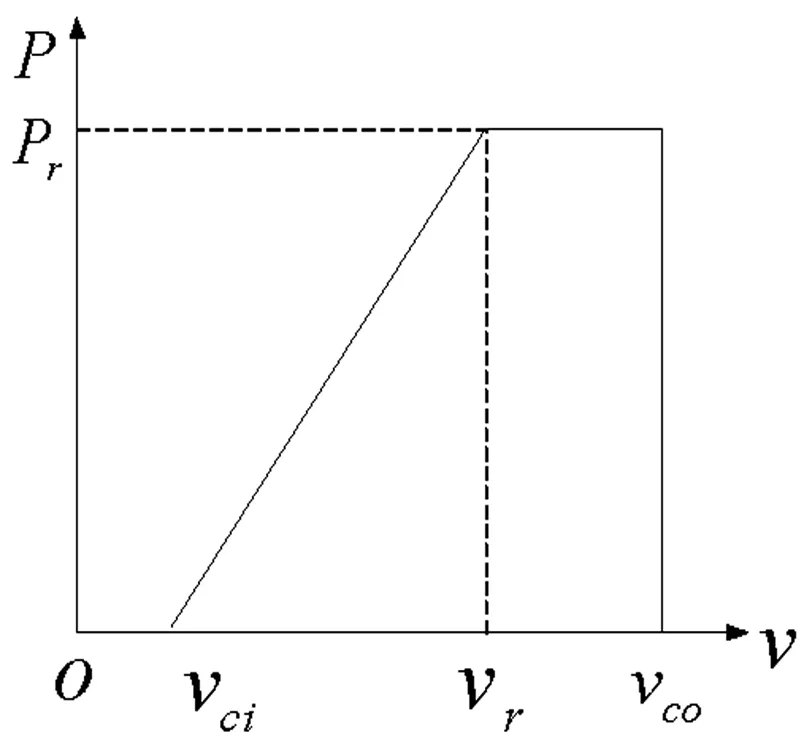
图1 风力发电机功率输出曲线
风电机组的输出功率与风速之间的分段函数表达式如下:
(5)
其中,V为风机轮毂高度处的风速;Vci为切入风速,Vco为切出风速,Vr为额定风速,Pr为风力发电机组额定输出功率。
本文采用风电场稳态简化模型(PZ模型)。在潮流计算中把风力机当成PQ节点,认为其有功功率就是风力机的机械功率,只与风速有关。因此风电场的有功出力Pf可以用运行的风机数乘以单台风机的出力Pw求得:
Pf=n×Pw
(6)
结合风速的概率密度函数可得风电场输出有功功率的概率密度为[1]:
(7)
其概率密度分布为三参数的Weibull分布函数。
1.3 光伏电站并网模型
本文假定光伏电池工作在最大功率点处。根据某一时刻的安装地点的太阳辐射量r,单个太阳能电池板面积A,以及电池组件的额定转换效率η,可以算出单块组件在时刻的输出功率P(单位为kW)[3]:
(8)
再根据整个光伏电站的光伏电池板元件数目n,即可算出时刻的整个光伏电站的出力为nP。在潮流计算中光伏电站可以按如下方式处理:将光伏电站直接当成普通电厂参与潮流计算,当白天光伏电场有出力时,所在的节点设为PV节点(电站本身装有无功补偿装置,具有一定的调压能力),当光伏电站的出力为0时(在非日照时间段内),该节点应转为PQ节点(有功出力P=0)参与潮流计算。
根据光照强度的概率密度函数,可得光伏电站输出有功功率的概率密度也呈现Beta分布:
(9)

1.4 负荷模型
在电网规划阶段,负荷的预测存在一定的不确定性,本文采用正态分布近似表示负荷预测结果(仅考虑有功),可以较好地反映负荷预测的不确定性。
(10)
其中:μ为数学期望,σ2为方差,P表示有功功率。
2 基于概率序列的含风光系统可靠性评估
2.1 电力系统生产模拟概率序列
电力系统中的供能元件(如发电机等)称为资源;耗能元件(如负荷等)称为需求。可以统一地用它们的可用容量为随机变量导出其分布规律[4,5]。取系统内各类元件的公共容量离散化步长为ΔC,设某元件m的额定容量为Cm,以ΔC对其序列化,令[4,5]
Sm=[Cm/ΔC]
(11)
其中[x]表示取不超过x的最大整数。
此元件共有Sm+1个状态,其中第i个状态的可用容量为:
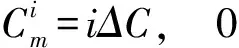
(12)
各状态对应相应的概率可以按照(7)、(9)、(10)式计算。假设风电场出力,光伏电场出力,负荷之间互相独立。
2.2 含风光系统可靠性评估
记:ΩREW为系统中所有风电、光伏发电机组集合;ΩG为系统中所有传统机组集合;ΩL为系统中所有负荷集合;ΩF为系统中所有线路集合。对于元件ξ∈ΩREW∪ΩL,其处于状态iξ的概率设为Pr(iξ) ,1≤iξ≤Sξ+1。
考虑网络约束时,系统的传统机组发电费用最小的最优潮流为:
(13)
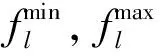
为提高计算速度,fl采用直流潮流求解。考虑到现实情况中,大部分线路潮流不会越界,所以式(13)中的最优潮流可以按照如下步骤加速求解:
(1)求解优化问题:
(14)
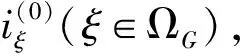
(15)
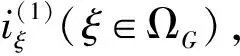
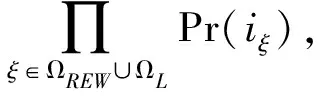
本文选取失负荷概率(LOLP)及停电电量期望值(EENS)作为可靠性评价指标。当然,除了上述的两种可靠性指标外,本算法还能得出每条线路上的有功潮流,在实际应用中可以灵活调用。
综合上述分析,基于概率序列和直流最优潮流的风光互补系统可靠性快速评估方法整体计算流程如下:
(1)确定系统的容量序列化步长ΔC(可取为各元件容量的最大公因子);
(2)对系统中所有元件容量进行序列化,并计算每个状态对应的概率;
(3)对风电、光伏、负荷元件所有可能的状态组合,实施步骤:(1)~(5);
(4)计算结束,统计LOLP和EENS。
3 算例分析
采用IEEE RBTS BUS6中的辐射型网络,而且只考虑其中30个节点的部分网络[1],电网拓扑结构如图2所示。本文中仿真设定的常规能源机组、风电场、光伏电站的装机容量分别为:8MW、3MW、0.6MW。
将常规能源机组从33kV母线节点接入,将风电场从18节点接入,将光伏电站从6节点接入。
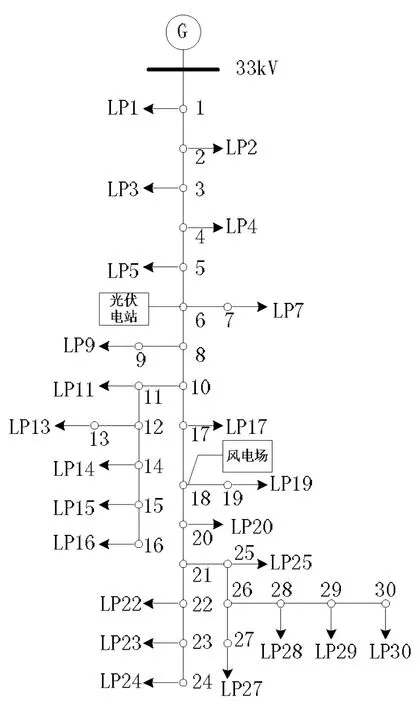
图2 IEEE RBTS BUS6电网拓扑结构
风电场参数如下所示:总装机容量5×600kW,风电机组的切入风速、切出风速、额定风速分别为:3m/s,25m/s,16m/s。风电场接入系统线路的参数为12.6+j24.96Ω,假定风电场空气密度为1.2245kg/m3,风力机扫掠面积为1840m2。
光伏电站参数如下所示:假定太阳能电池安装地点地理纬度为33.38°,太阳能电池组件的基本参数为180峰瓦,总装机容量为600kW,电池板的外形尺寸为1580×793×50(mm),装设于正南方。太阳能阵列的倾斜角为0°,订正后的大气透明度P2=0.7。电池组件的额定转换效率为13%。
负荷参数:按文献[6]提供的负荷数据,以正态分布(简化为0,±1%,±2,±3%七个离散点)来考虑负荷预测的不确定性。取计算步长ΔC=1.0MW。
采用MATLAB编程,在主频为2.5GHz,RAM为2GB的计算机上,实现仿真分析。为了方便比较,对该系统算例再采用蒙特卡罗方法进行仿真,两种方法计算的可靠性指标值和计算时间如表1所示。
由下表可以看到,本文提出的基于概率序列的含风光系统可靠性评估方法与蒙特卡罗方法的计算结果精度相仿,但是计算消耗时间仅为蒙特卡罗方法的1/9左右。仿真计算结果说明该评估方法具有精度高、速度快的显著优点。

表1 可靠性指标计算结果和计算时间
4 总结
本文出于电力系统规划阶段对可靠性评估的精度要求相对不高、时间代价不能太大这两点要求,提出一种基于概率序列的含风光电力系统可靠性评估方法。在MATLAB中的仿真计算表明,相对于蒙特卡罗方法,该方法不仅可以保证可靠性分析的计算精度,而且能够显著提高计算速度,大大提高了电力系统规划阶段供电可靠性评估的效率,具有较强的工程实用价值。

