一个新的钢筋混凝土损伤塑性模型*

徐鹏飞，刘殿书，张英才

(1.中国矿业大学(北京) 力学与土木工程学院，北京 100083； 2.河南工业大学土木建筑学院，河南 郑州 450001； 3.河南理工大学土木工程学院，河南 焦作 454000)

钢筋混凝土结构是土木工程中应用最普遍的结构形式之一，随着社会的不断发展，一些建构筑物失去价值后需利用控制爆破技术将其拆除，在城市建构筑物和人口密集、倒塌空间受限、周边环境复杂等情况下，常常采用数值模拟技术对爆破效果进行预测以优化爆破设计方案。目前，LS-DYNA软件中没有一种现成的材料模型能模拟钢筋混凝土，并同时考虑钢筋混凝土在受拉、受压以及率荷载下的力学性能，随着钢筋混凝土结构高度、体积、配筋率越来越大，采用分离式模型和组合式模型需耗费大量计算资源和时间，且钢筋与混凝土相互作用比较复杂，数值模拟结果往往难以达到预期爆破效果，为钢筋混凝土结构建构筑物的安全精确爆破埋下一定隐患，因此，钢筋混凝土材料模型一直是研究的重点与难点。

沈新晋等[2]以ABAQUS软件为平台，采用应变协调假设和强度等效假设，给出了一个描述钢筋混凝土材料与结构损伤塑性分析的本构模型，认为钢筋屈服后，立刻进入下降阶段，不考虑钢筋与混凝土相互作用引起的受拉刚化效应及受压箍筋约束效应。骈超等[2]借助ABAQUS软件中混凝土损伤本构模型，利用刚度等效原则将钢筋混凝土视为连续均质材料，对钢筋混凝土材料的本构关系进行分段线性简化，对钢筋与混凝土相互作用引起的受拉刚化效应进行了修正，但未考虑钢筋混凝土受压时的箍筋约束效应以及配筋率对受拉刚化效应的影响。宋伟等[3]在已有连续损伤理论的基础上，提出了综合考虑混凝土损伤、钢筋混凝土粘结滑移、以及受拉刚化效应等因素的钢筋混凝土拉伸本构模型。殴碧峰等[4]考虑钢筋和混凝土的相互作用，在Baant等提出的混凝土微平面模型的基础上通过引入钢筋的影响提出了一个钢筋混凝土动态本构模型。商霖等[5]提出了理想情况下钢筋混凝土本构关系可由混凝土材料黏弹性本构关系与一个依赖于增强材料特性的常量G的乘积确定的思想，得到了单向加筋、正交双向加筋和正交三向加筋混凝土的损伤型动态本构关系。孔丹丹等[6]在Zhao和Weng建立的纤维增强等效材料的等效模量理论的基础上，针对钢筋混凝土材料的力学特征，提出了钢筋单方向、三方向分布情况下钢筋混凝土材料的平均等效模量的简化公式。

本文中，在已有研究的基础上，考虑钢筋混凝土受拉刚化效应、配筋率对受拉刚化效应的影响和钢筋混凝土受压箍筋约束效应，采用组合模量方法对钢筋混凝土复合材料进行模量等效，并对钢筋混凝土本构关系进行分段线性简化，借助LS-DYNA软件中混凝土损伤塑性模型，建立钢筋混凝土损伤塑性模型，在实验验证的基础上，应用此模型对一双切口钢筋混凝土烟囱同向延时爆破拆除效果进行数值模拟。

1 钢筋混凝土本构模型

1.1 钢筋混凝土拉伸力学行为

图1给出了一个含有钢筋和混凝土的二维方形钢筋混凝土样本材料单元[3]。图1中正方形边长为单位长度1，钢筋截面与混凝土截面的面积比为μ(配筋率)，0<μ<1，应力荷载如图所示。钢筋所受应力为σt,steel，混凝土所受应力为σt,concr。图1中的右图为简化的钢筋混凝土材料单元模型。由于平衡关系，CD的对边AB上所受的载荷相同(为了简单起见，没标出AB边上的载荷)。

图1 钢筋混凝土等效材料单元体示意图Fig.1 Schematic diagram of reinforced concrete equivalent material unit

模型采用应变协调假设，即假设钢筋和混凝土间粘合完好，二者的应变量相等:

εconcr=εsteel=ε

(1)

由静力关系可得钢筋混凝土等效材料的组合应力σt为:

σt=[σt,steelμ+σt,concr(1-μ)]

(2)

钢筋混凝土等效均质材料单轴受拉应力在达到混凝土开裂应力前，认为钢筋与混凝土均处于弹性工作状态，当混凝土开始出现裂缝时，近似认为混凝土达到峰值拉应力，此时开裂应力为：

(3)

式中：Ee为钢筋混凝土等效材料单元组合模量，Ee=[Esteelμ+Econcr(1-μ)]；Esteel为钢筋弹性模量，Econcr为混凝土弹性模量。

在等效材料单元应力大于开裂应力但未达到钢筋屈服强度时，钢筋仍处于弹性阶段，假定钢筋与混凝土之间无相对滑移，通过调整钢筋刚度来模拟受拉刚化效应，荷载全部由钢筋来承担。考虑钢筋受拉刚化效应，混凝土峰值应力为：

σt2=εt,limψμEsteel

(4)

式中：εt,lim为混凝土极限拉应变，由钢筋混凝土等效材料配筋率决定，配筋率小于1%时，可取1×10-3，配筋率大于1%时，可取σt,steel/Esteel[3,7]，本文中为考虑受拉刚化效应的不均匀系数，取值为5[8]。

随着应变增加，钢筋应力逐渐增大，直到钢筋达到屈服应力。此时钢筋混凝土等效材料单元应力为：

σt3=μσt,steel

(5)

对应的应变εt3为：

(6)

假设钢筋达到屈服强度后，混凝土已经全部拉裂，钢筋进入颈缩阶段，单元发生较大变形，钢筋混凝土等效材料受拉应力进入下降阶段。钢筋混凝土等效均质材料单轴受拉应力应变曲线见图2(a)。

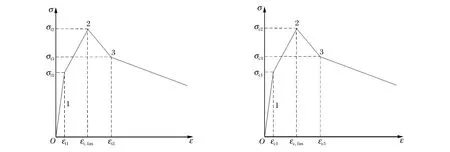
图2 等效材料应力-应变关系曲线示意图Fig.2 Illustration of stress-strain relationship of the equivalent material

1.2 钢筋混凝土压缩力学行为

假定混凝土的弹性极限应力为0.3倍混凝土抗压强度，钢筋混凝土等效材料应力达到初始屈服应力σc1：

σc1=[Esteelμ+Econcr(1-μ)](0.3Fc,concr)/Econcr

(7)

式中：Fc,concr为素混凝土的抗压强度。

对应的应变εc1为：

εc1=σc1/E=0.3Fc,concr/Econcr

(8)

当等效材料单元应力超过初始屈服应力后，混凝土开始出现塑性，而钢筋依然处于弹性阶段。当混凝土达到约束混凝土峰值应力，认为纵向钢筋达到屈服应变，钢筋应力维持在受压屈服强度，此时钢筋混凝土等效材料达到最大屈服应力σc2：

(9)

约束混凝土峰值应力和峰值应变为[9]:

(10)

式中：λ为箍筋综合约束指标，λ=μσt,steel/Fc,concr。

当钢筋混凝土等效材料轴压应变超过εc3时，由于箍筋的约束作用使得混凝土峰后应力应变曲线延性增加。根据《混凝土结构设计规范2010》可知，当混凝土强度等级在C30～C60时，混凝土的极限压应变εc3与峰值压应变εc2之比可近似认为是2，极限压应变对应的混凝土强度取0.15倍的峰值压应力，在此过程中认为钢筋一直保持屈服应力不变。钢筋混凝土等效材料在极限压应变时的应力σc3为：

(11)

当钢筋混凝土等效材料应力小于极限压应力时，近似认为钢筋混凝土等效材料受压应力进入下降阶段。钢筋混凝土等效材料单轴受压应力应变曲线见图2(b)。

2 钢筋混凝土损伤塑性模型

2.1 混凝土损伤塑性模型

混凝土损伤塑性模型是基于以下应力应变关系[10]：

(12)

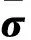
(13)

式中：De为基于弹性模量E和泊松比ν的弹性刚度张量；ε为应变张量；εp为塑性应变张量。

(14)

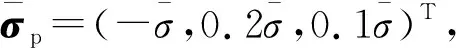
塑性模型是基于有效应力，与损伤无关。塑性模型[11]可以通过屈服函数，流动法则，硬化变量的演化法则以及加卸载条件进行描述。

屈服函数的形式可以表示为：

(15)

式中：qh1(κp)和qh2(κp)为控制屈服面大小和形状演化的无量纲函数，κp为硬化变量。

流动法则可以表述为：

(16)

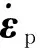
硬化变量κp的速率与塑性应变率的演化规律有关，加卸载条件为：

(17)

损伤模型[12]可以通过损伤加载函数，加卸载条件以及拉伸和压缩损伤变量的演化规律进行描述。对于拉伸损伤方程可以表示为：

(18)

对于压缩损伤方程可以表示为：

(19)

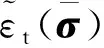
混凝土损伤塑性模型中，应变率效应通过引入因子αr(αr>1)， 值越大，损伤延迟的发生和强度提高越大。对于混凝土应变率效应，采用动力增大系数曲线体现动荷载作用下材料屈服强度的提高。混凝土抗压强度的动态增大系数采用欧洲规范CEB建议的公式[13]计算，混凝土抗拉强度增大系数采用修正的CEB公式[14]计算。因此，αr可以定义为：

αr=(1-αc)αrt+αcαrc

(20)

式中：αrt和αrc为拉伸应变率效应因子和压缩应变率效应因子；αc为一标量(0<αc<1)，αc=1表示仅压缩，αc=0表示仅拉伸。

2.2 模型参数修改

LS-DYNA中混凝土损伤塑性模型参数及部分模型参数默认值[10]见表1。表1中：MID代表材料编号，Type代表损伤类型，ρ为密度，E为弹性模量，ν为泊松比，Ecc为偏心距，QH0为初始硬化参数，Ft为单轴抗拉强度，Fc为单轴抗压强度，Hp为硬化参数，Ah、Bh、Ch、Dh为硬化延性参数，As、Bs为软化延性参数，Df为流动法则参数，fco为应变率相关参数，Wf为线性损伤公式下拉伸阀值位移，Wf1、Ft1为双线性损伤公式下第二部分对应的拉伸位移阀值和拉伸强度阀值，Sf为应变率标识，Ff为失效方式标识。混凝土损伤塑性模型参数分别控制着应力应变曲线的弹性、硬化和软化三个阶段。

表1 LS-DYNA混凝土损伤塑性模型默认参数Table 1 Default parameters of concrete damage plasticity model

本文中，依据钢筋混凝土在单轴受拉、受压作用下的等效本构关系，基于LY-DYNA混凝土损伤塑性模型，对弹性模量E、抗拉强度Ft、抗拉强度阀值Ft1、断裂位移Wf、硬化参数Bh、抗压强度Fc、损伤延性参数As等8个参数进行修改，得到钢筋混凝土损伤塑性模型。具体的[11-12]：

E=Ec;Fc=σc2;Ft=σt2;Ft3=σt3;Wf=εt3hx/0.15,h为单元网格尺寸，x为钢筋混凝土与混凝土的等效抗拉强度之比；Bh=0.007 82ln [(εc2+1.242)/2.107]；Esoft=38.12As-1.11，Esoft为受压软化模量，由钢筋混凝土等效材料受压应力应变曲线中对应的特征点2和3应力应变数据计算得出。

3 钢筋混凝土损伤塑性模型验证

3.1 钢筋混凝土轴压短柱实验

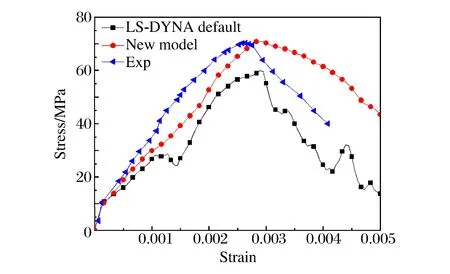
图3 钢筋混凝土等效轴压柱应力应变曲线Fig.3 Stress-strain curve of reinforced concrete equivalent axial compression column

图4 钢筋混凝土等效简支梁荷载位移曲线Fig.4 Load displacement curve of reinforced concrete simple supported beam

钢筋混凝土短柱尺寸为150 mm×150 mm×450 mm，混凝土抗压强度fc=63.1MPa，配筋率为0.84%，纵筋屈服强度为548.1 MPa，箍筋采用HPB235，配箍率为0.82%，配箍特征值为0.03，具体见文献[15]。

根据以上实验参数，在数值模型中设置：钢筋混凝土等效材料的组合模量为38.52 GPa；εc2=2.6×10-3；Fc=σc2=68.7 MPa；εc3=2εc2=5.2×10-3；σc3=58.6 MPa；Ft=σt2=8.4 MPa；Ft1=σt3=4.49 MPa；Bh=4.7×10-3；As=7.7；Wf=25εt3σt2/(0.15σt,concr)=0.79 mm。

图3给出了钢筋混凝土轴压短柱采用钢筋混凝土损伤塑性模型和默认参数混凝土损伤塑性模型的数值模拟与实验结果，可以看出，钢筋混凝土损伤塑性模型数值模拟结果与实验结果较为吻合。

3.2 简支梁压弯实验

钢筋混凝土简支梁梁长1 400 mm，支座间距为1 200 mm，梁截面为矩形，宽150 mm，高200 mm。混凝土标号为C25，保护层厚度为25 mm。钢筋混凝土梁受拉和受压均配置2跟∅10钢筋(HRB335)，箍筋选用∅6@150(HPB235)，梁受拉与受压配筋率和体积配箍率分别为0.522 5%和0.628%。实验采用两点加载，加载速率为10 mm/s，单调加载，简支梁内混凝土的应变率将达到0.01 s-1以上，具体见文献[16]。

根据以上实验参数，在数值模型中设置：钢筋混凝土等效材料的组合模量为38.52 GPa，εc2=2.4×10-3；Fc=σc2=31.6 MPa；εc3=4.8×10-3；σc3=27.4 MPa；Ft=σt2=5.225 MPa；Bh=4.6×10-3；As=15.8；Ft1=σt3=1.75 MPa；Wf=25εt3σt2/(0.15σt,concr)=0.58 mm。

图4给出了钢筋混凝土简支梁采用钢筋混凝土损伤塑性模型和默认参数混凝土损伤塑性模型的数值模拟计算结果与实验结果，可以看出，钢筋混凝土损伤塑性模型数值模拟结果与实验结果基本一致。

4 应 用

图5 钢筋混凝土烟囱有限元模型Fig.5 Finite element of reinforced concrete chimney

某钢筋混凝土烟囱高210 m，烟囱底部筒体外半径为9.45 m，壁厚600 mm，烟囱顶部外半径为3.35 m，壁厚250 mm，混凝土标号C30，竖向筋截面配筋率在0.42%～0.66%之间，环向筋配筋率平均为0.45%。烟囱上部爆破切口布置在90 m处，切口角度210°，切口高度为2.5 m，正梯形切口，定向窗角度为30°，底部爆破切口角度为216°，切口高度为3.5 m，正梯形切口，定向窗角度为30°，爆破方案设计上切口先于下切口3 s起爆。

钢筋混凝土烟囱有限元模型由3部分组成：筒体、钢筋和爆破切口，建模过程中混凝土采用Solid164单元，钢筋采用Beam161单元，由于烟囱竖向筋和环向筋配筋率不同，只能对环向配筋进行简化等效，竖向筋则按剩余配筋率正常建立，竖向筋与筒体之间采用分离式共节点的处理方式，钢筋与混凝土共计472 440个单元，钢筋混凝土烟囱有限元模型见图5。钢筋材料采用弹塑性硬化模型，密度为7 850 kg/m3，屈服强度为335 MPa，弹性模量为200 GPa，泊松比为0.3。筒体采用钢筋混凝土损伤塑性模型，钢筋混凝土损伤塑性模型参数见表2。地面采用刚体模型，密度为2 000 kg/m3，弹性模量为30 GPa，泊松比为0.2。烟囱重力采用关键字*LOAD_BODY_Y(Y方向)来实现。钢筋与刚体地面接触采用关键字*CONTACT_NODES_TO_SURFACE接触定义，防止钢筋触地穿透地面，筒体与刚体地面采用关键字*CONTACT_ERODING_SINGLE_SURFACE接触定义。爆破切口的形成采用关键字*MAT_ADD_EROSION中的时间控制参数定义，爆破切口范围内单元一次性控制删除，不考虑炸药爆炸以及毫秒延时对切口形成的影响。钢筋和混凝土材料失效均由应变控制，钢筋材料失效应变设为0.05，混凝土材料失效应变设为0.004。

表2 新钢筋混凝土损伤塑性模型参数Table 2 Parameters of new concrete damage plasticity model

采用钢筋混凝土损伤塑性模型，图6给出高耸双切口钢筋混凝土烟囱同向延时爆破拆除数值模拟倒塌过程与实际高速摄影观测结果，可以看出，实际高速摄影观测结果不论在倒塌运动状态还是在倒塌时间上均与数值模拟结果相符，说明采用钢筋混凝土损伤塑性模型模拟钢筋混凝土烟囱爆破拆除不仅简化了建模工作量，提高了计算效率，且计算结果与实际较为吻合，同时也证实了钢筋混凝土损伤塑性模型参数计算选取的正确性及合理性。

图6 烟囱爆破拆除实际倒塌与数值模拟过程对比Fig.6 Comparison between numerical simulation and actual collapse process of chimney blasting demolition

5 结 论

(1)借助LS-DYNA有限元软件中混凝土损伤塑性模型，采用组合模量的方法给出了一个钢筋混凝土损伤塑性模型，该模型综合了混凝土受拉和受压损伤、应变率效应，考虑了钢筋混凝土受拉刚化效应、受压箍筋约束效应以及配筋率对受拉刚化效应的影响，在保证钢筋混凝土受力性能的前提下，极大简化了建模工作量。(2)钢筋混凝土结构数值模拟采用钢筋混凝土材料模型受力更合理，在不影响计算精度的前提下，提高了计算效率。(3)拆除爆破工程具有唯一性和一定的高危性，数值模拟作为一种重要的分析手段发挥的作用愈加明显，本文采用钢筋混凝土材料模型模拟结果与实际高速摄影观测结果较为吻合，给出的钢筋混凝土损伤塑性模型可为钢筋混凝土结构爆破拆除工程数值模拟提供参考和借鉴。